Одной из наиболее важных стратегий является организация данных, хотя, на первый взгляд, это понятно и без слов. Иначе говоря, все должны автоматически упорядочивать данные из условий задачи. В жизни мы делаем это подсоз­нательно каждый день.

Так, приступая к заполнению налоговой декларации каж­дую весну, мы автоматически организуем данные в определенном порядке без всяких подсказок. От того, как будут организованы квитанции, чеки, формы W-2 и т.п., сильно зависит заполнение сложных форм налоговой отчетности.

Большинство людей составляют тщательно организованный список покупок, прежде чем отправиться в супермаркет. Они могут разбивать покупки по категориям, по месту расположения в магазине или по степени необходимости. Аналогичным образом, отправляясь в турпоездку, мы чаще всего составляем перечень того, что хотим посмотреть. При этом список можно изложить на бумаге или просто держать в голове.

Когда крупные организации проводят опросы, нет ничего необычного в том, что они получают разные результаты, — все зависит от того, как в каждом случае организуются одни и те же данные.

В задачах, включающих множество данных, людей нередко приводит в замешательство представление этих данных. Умение организовывать данные в логичной и ясной форме очень помогает решению задач. Рассмотрим одну из задач, где применяется эта стратегия.

Группа археологов ведет раскопки. Они ежедневно на протяжении 15 дней находят множество осколков глиняной посуды:

13, 45, 12, 47, 8, 18, 13, 27, 98, 11, 23, 67, 51, 14, 6.

Чему равно медианное количество найденных ими осколков глиняной посуды?

При таком представлении количества ежедневных находок решить данную задачу практически невозможно. Организуем данные более логичным образом — в порядке возрастания:

6, 8, 11, 12, 13, 14, 18, 23, 27, 45, 47, 51, 69, 98.

Теперь найти медиану не представляет труда. Это среднее число, в нашем случае восьмое, или 18.

Рассмотрим еще одну задачу, где очень важна организация данных.

Джек и Марлин хотят вступить в клуб любителей кино на DVD. Они получают два предложения. Клуб Freedom Movie взимает вступительный взнос в размере $20, а потом берет $6,20 за каждый фильм. Клуб New Look не требует вступительного взноса, однако берет $8,10 за каждый DVD. Джек решает присоединиться к клубу Freedom Movie, а Марлин — к клубу New Look. Сколько DVD каждый из них должен купить, прежде чем Марлин истратит больше Джека? Насколько больше она истратит?

Чтобы решить задачу, организуем данные в три колонки:

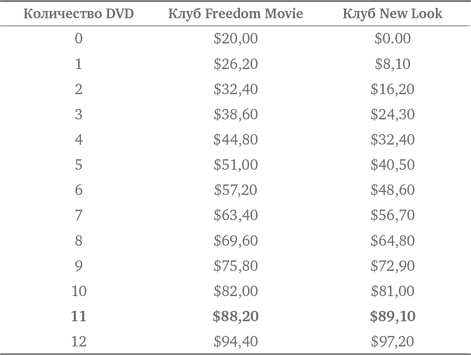
Когда они купят по 11 DVD, Марлин истратит больше денег, чем Джек. Марлин придется заплатить $89,10 — $88,20, или на 90 центов больше. Ответы на оба вопроса легко найти, проанализировав представленные в табличной форме данные.

А вот геометрическая задача, решить которую можно только при тщательной организации данных.

Треугольник имеет сумму сторон и периметр, равные 12. Чему равны длины его трех сторон?

Подготовим и организуем перечень данных, обозначив стороны треугольника, как A, B и C. Начнем с A = 1 и перечисления всех возможностей для A = 1. Затем сделаем то же самое для A = 2 и т.д.

В этом перечне все тройки чисел дают сумму, равную 12. Не забывайте, однако, что в треугольнике сумма любых двух сторон всегда больше третьей стороны, иначе треугольник не может существовать. Это условие исключает большее число сочетаний. Единственные три возможности — это 2-5-5, 4-4-4 и 3-4-5. Представление данных в упорядоченном виде значительно облегчает решение задачи.

В этой главе мы представим задачи, которые наиболее эффективно решаются путем организации данных логичным образом. Хотя некоторые из них можно решить и другими способами, они приводятся для демонстрации пре­имуществ этого вроде бы необычного метода решения.

Задача 7.1

Между двумя баскетбольными командами устраивают конкурс на лучшее исполнение штрафных бросков. В финал выходят Робби и Сэнди. Победителем становится тот, кто первым выполнит подряд два успешных штрафных броска или в целом три штрафных броска. Сколько комбинаций бросков может привести к победе?

Обычный подход

Большинство начинает с попыток найти все возможные комбинации, которые могут привести к победе. Однако непонятно, как определить, все ли комбинации учтены. Это довольно проб­лематичная задача.

Образцовое решение

Воспользуемся стратегией организации данных и составим два исчерпывающих перечня путей достижения победы каждым игроком. Первый перечень показывает результаты, когда первый бросок делает Робби, второй — когда первый бросок делает Сэнди.

Существует 10 возможных комбинаций, на которых конкурс завершается. Исчерпывающий перечень комбинаций упорядоченно и наглядно представляет возможности.

Задача 7.2

Сколько треугольников изображено на рис. 7.1?

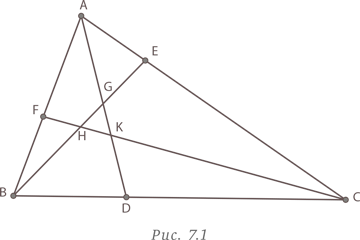
Обычный подход

Как правило, люди начинают подсчитывать треугольники в том или ином порядке, но без определенной сис­темы. Чаще всего это приводит к путанице и неуверенности в том, все ли треугольники учтены. Другой традиционный подход предполагает использование формальных методов подсчета. В этом случае определяются комбинации, которые могут быть образованы шестью линиями, и исключаются комбинации, образующиеся в результате совпадений. Количество комбинаций из шести линий по три равно 6C3 = 20. Из этого результата нужно вычесть три совпадения (по вершинам). Таким образом, в фигуре на рисунке 17 треугольников.

Образцовое решение

Для упрощения задачи преобразуем фигуру, будем постепенно добавлять линии и считать, что получается в результате использования такой формы организации данных. Иначе говоря, мы будем подсчитывать треугольники, образующиеся при добавлении каждой части. Начнем с исходного треугольника ABC. Итак, в начале мы имеем всего один треугольник.

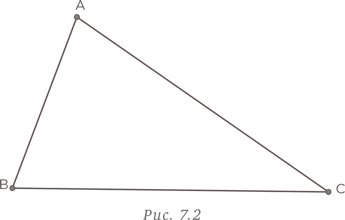
Теперь рассмотрим треугольник ABC с одной внутренней линией AD. У нас получилось два новых треугольника ABD и ADC.

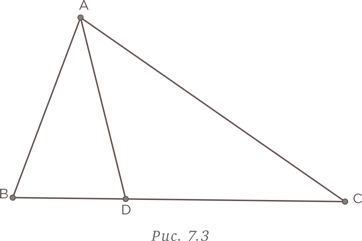
Добавим еще одну внутреннюю линию BE и подсчитаем все новые треугольники, имеющие сторону BE.

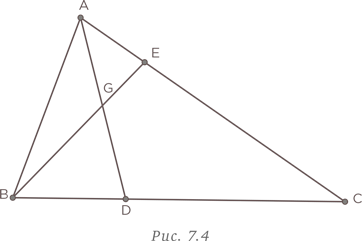
Таким же образом добавим линию CF и опять подсчитаем новые треугольники, имеющие сторону CF.

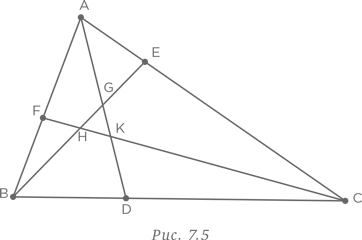
Представим полученные результаты в табличной форме.

Общее количество перечисленных выше треугольников равно 17.

Задача 7.3

Дана последовательность 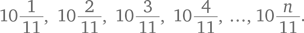Найдите положительное целое число n, при котором произведение первых n членов последовательности превышает 100 000.

Обычный подход

В этом случае обычно прибегают к методу проб и ошибок и начинают добавлять члены в последовательность и перемножать их до тех пор, пока произведение не превысит 100 000. Такой подход трудоемок, и его точно нельзя назвать изящным.

Образцовое решение

Напишем сначала произведение первых n членов данной последовательности, что в определенном смысле будет организацией и представлением наших данных в более удобной форме:

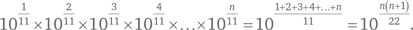
«Превышает 100 000» означает, что нам нужно число, большее, чем 105, а это происходит, только когда 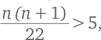или n (n + 1) > 110. Когда n ≤ 10, мы получаем n (n + 1) ≤ 110. Таким образом, наименьшее целое значение n, при котором выполняется условие задачи, равно 11.

Задача 7.4

Джером открыл свое первое предприятие по прокату каяков. За прокат он берет почасовую оплату. Каякам присваиваются идентификационные номера, на каждом из них стоят три цифры. Первая цифра — это номер предприятия, а именно 1. Номера у каяков не могут повторяться, а три цифры должны располагаться в возрастающем порядке. Ноль использовать нельзя. Вскоре Джером обнаружил, что использовал все возможные сочетания, которые удовлетворяют условиям. Какое максимальное количество каяков может быть у Джерома?

Обычный подход

Самый распространенный подход — выписывание всех возможных трехзначных чисел, удовлетворяющих условиям задачи. Но как узнать, все ли эти числа учтены? Существует ли метод, обеспечивающий гарантированное решение? Обычный подход явно не самый эффективный!

Образцовое решение

Представим наши данные в табличной форме:

Джером может иметь не более чем 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 каяков.

Задача 7.5

Фермер везет яблоки на рынок. Яблоки уложены в шесть ящиков. Весы на пункте взвешивания могут принять за раз только пять ящиков. Нам дают результаты шести взвешиваний:

Ящик B + ящик C + ящик D + ящик E + ящик F = 200 фунтов;

Ящик A + ящик C + ящик D + ящик E + ящик F = 220 фунтов;

Ящик A + ящик B + ящик D + ящик E + ящик F = 240 фунтов;

Ящик A + ящик B + ящик C + ящик E + ящик F = 260 фунтов;

Ящик A + ящик B + ящик C + ящик D + ящик F = 280 фунтов;

Ящик A + ящик B + ящик C + ящик D + ящик E = 300 фунтов.

Сколько фунтов яблок в каждом ящике?

Обычный подход

Эту задачу можно решить алгебраически, составив шесть уравнений с шестью неизвестными:

B + C + D + E + F = 200;
A + C + D + E + F = 220;
A + B + D + E + F = 240;
A + B + C + E + F = 260;
A + B + C + D + F = 280;
A + B + C + D + E = 300.

Решение шести уравнений довольно трудоемко, поэтому попробуем поискать другой подход к этой задаче.

Образцовое решение

С помощью нашей стратегии организации данных можно упростить решение задачи и сделать его изящным. Начнем с представления данных в табличной форме:

Мы опять получили довольно громоздкий набор уравнений, но можно посмотреть на них с другой точки зрения и организовать данные вертикально, просуммировав колонки в вертикальном направлении:

5A + 5B + 5C + 5D + 5E + 5F = 1500.

Разделив обе стороны уравнения на 5, мы получаем:

A + B + C + D + E + F = 300.

Однако шестое взвешивание в таблице показывает, что A + B + C + D + E = 300 фунтам. Следовательно, ящик F должен весить 0 фунтов. Обратимся затем к пятому взвешиванию, которое показывает, что A + B + C + D + F = 280 фунтам. Однако мы уже знаем, что F = 0, а значит A + B + C + D = 280.

Вернемся к шестому взвешиванию — A + B + C + D + E = 300, вычтем из него последнее уравнение и получим E = 20 фунтов.

Из четвертого взвешивания следует, что A + B + C + E + F = 260. Подставив в это уравнение уже известные значения F и E, мы получим A + B + C + 20 + 0 = 260, или A + B + C = 240. Подставляя это значение в пятое взвешивание, находим D = 40.

Если вычесть уравнение третьего взвешивания из уравнения четвертого взвешивания, то, зная, что F = 0, мы получаем:

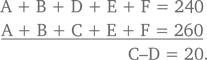
Поскольку D = 40, мы получаем C = 60.

Подставим известные значения в уравнение первого взвешивания: B + C + D + E + F = 200 = B + 60 + 40 + 20 + 0. Таким образом, B = 80.

Поступив аналогичным образом с уравнением второго взвешивания, получим A = 100.

Использование табличной формы сделало данные более понятными и позволило решить задачу путем логических рассуждений.

Задача 7.6

Даны трехзначные числа, которые составлены исключительно из нечетных цифр. Чему равна сумма всех этих чисел?

Обычный подход

Обычно при решении задачи такого типа начинают составлять список нечетных чисел в том или ином порядке, а потом долго складывают их.

Образцовое решение

Главное здесь — организовать числа логичным образом. Например, наш список может выглядеть так: 111 + 113 + 115 + 117 + 119 + 133 + 135 + 137 + 139 + … + 511 + 513 + 515 + 517 + 519 + … + 991 + 993 + 995 + 997 + 999. Поскольку всего пять цифр могут находиться в каждом из трех разрядов, существует 5 × 5 × 5 = 125 возможных чисел. Если подойти к делу организованно, то можно складывать эти числа парами: первое и последнее, второе и предпоследнее и т.д. Сумма каждой из этих пар равна 1110. В нашем списке пар 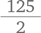чисел. Таким образом, сумма этих чисел составляет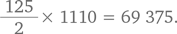  

Данные можно организовать по-другому и также получить довольно изящное решение. Мы уже определили, что сложить нужно 125 целых чисел, каждое из которых состоит из трех цифр, а значит всего нам необходимо принять во внимание 375 цифр. Понятно, что каждое из пяти нечетных цифр — 1, 3, 5, 7 и 9 — встречается 75 раз, т.е. 25 раз в каждом разряде (в разряде сотен, десятков и единиц). Это можно представить в виде формулы следующим образом:

25 [100 (1 + 3 + 5 + 7 + 9) + 10 (1 + 3 + 5 + 7 + 9) + 1 (1 + 3 + 5 + 7 + 9)] = 25 × 25 × (100 + 10 + 1) = 69 375.

В каждом из приведенных примеров организации данных решение задачи становится значительно более изящным, чем в случае использования лобового метода.

Задача 7.7

Допустим, у нас есть 11 линий, лежащих в одной плоскости, при этом три линии проходят через точку P, а три линии имеют общую точку Q. Никакие другие три линии, кроме этих, не пересекаются. Чему равно минимальное количество точек пересечения этих 11 линий при таких условиях?

Обычный подход

Чаще всего эту задачу пытаются решить методом проб и ошибок, но довольно большое количество линий (11) делает такой подход проб­лематичным. Таким образом, должен быть какой-то другой, более эффективный способ решения подобной задачи.

Образцовое решение

Чтобы решить такую задачу, нужно организовать линии логичным образом. Начнем с построения трех линий, пересекающихся в точке P, как показано на рис. 7.6.

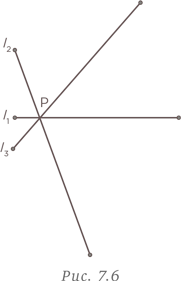
Повторим эту процедуру с точкой Q, построив линии l3||l4 и l2||l5, как показано на рис. 7.7.

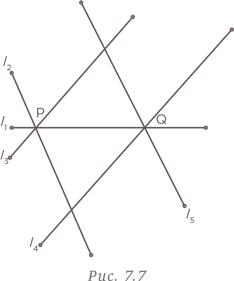
Затем проведем шесть оставшихся линий параллельно линии l2. Это показано на рис. 7.8. Каждая из этих линий добавляет три новые точки пересечения.

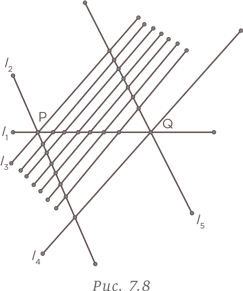
Таким образом, в результате организации исходных данных логичным образом мы получаем следующее количество точек пересечения: 6 × 3 + 4 = 22.

Задача 7.8

Если напечатать все числа от 1 до 1 000 000, сколько раз в них встретится цифра 8?

Обычный подход

Обычно в ответ на такой вопрос, который кажется ошеломляющим, начинают составлять список чисел без какого-­либо намека на их организацию. При таком подходе решение зависит от того, удастся ли увидеть какую-нибудь закономерность в числовом ряду.

Образцовое решение

Лучшая стратегия здесь заключается, пожалуй, в организации данных таким образом, чтобы можно было выявить любую закономерность в списке, если она существует.

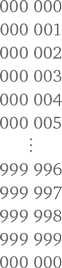
В представленных выше шести разрядах миллиона цифры 0, 1, 2, 3, 4, …, 8 и 9 используются равное количество раз. Это понятно потому, что каждую «комбинацию» можно составить из каждой из 10 цифр. Таким образом, цифра 8 должна появиться в случаев, или 600 000 раз.

Задача 7.9

У продавца двое часов, которые бьют полночь одновременно. Однако одни часы спешат на 1 минуту в час, а другие отстают на 1 минуту в час. Если такая разница сохранится и дальше, то через какое время их показания совпадут?

Обычный подход

Первая мысль — составить уравнение. Если обозначить за x время, через которое показания часов совпадут, то мы получим 12 + x = 12 – x. Решение этого уравнения дает 2x = 0, и x = 0. От такого решения толку мало.

Образцовое решение

В сутках 24 часа, за это время часы A уйдут вперед на 24 минуты, а часы B отстанут на 24 минуты. Через пять дней часы A уйдут вперед на 5 × 24 = 120 минут, или на 2 часа. В свою очередь часы B будут отставать на 120 минут, или 2 часа каждые пять дней. Воспользуемся нашей стратегией и представим данные в табличной форме.

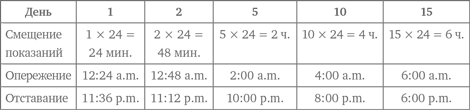
Из таблицы видно, что на табло обоих часов будет 6:00 в конце 15-го дня. Конечно, одни из них будут показывать 6:00 a.m., а другие — 6:00 p.m. Тем не менее показания совпадут, а именно это и требовалось найти в задаче.

Задача 7.10

Сколько существует положительных трехзначных нечетных чисел, произведение цифр которых дает число 252?

Обычный подход

Чаще всего начинают искать тройки множителей, произведение которых равно 252. Иначе говоря, выписывают наборы из трех цифр, дающие при перемножении 252. Это следует делать упорядоченно, начиная с цифр 1, 1, 252, за которыми следуют 1, 2, 126, затем 1, 3, 84, за ними 1, 4, 63 и т.д. Можно перебирать цифры таким образом до тех пор, пока не попадется хотя бы один набор, который даст нечетное трехзначное число. Не исключено, однако, что таких наборов несколько. Можно ли с уверенностью сказать, что найдены все возможные варианты? «Лобовой» подход не дает нам такой уверенности.

Образцовое решение

Попробуем применить нашу стратегию организации данных. Можно разложить число 252 на множители 2 × 2 × 3 × 3 × 7. Если одна из цифр 7, то другие цифры должны давать при перемножении 36, т.е. 4 и 9 или 6 и 6, поскольку все другие комбинации включают в себя множители, имеющие более одного знака. Комбинируя эти цифры с 7, мы находим пять чисел, которые удовлетворяют условиям задачи. Это 749, 479, 947, 497, 667 — все они нечетные трехзначные числа, а произведение их цифр равно 252.

Задача 7.11

Какое число в следующем ряду самое большое и какое число стоит на втором месте по величине?

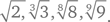
Обычный подход

В наши дни рука автоматически тянется к калькулятору. Однако найти ответ может быть не так просто, как кажется, поскольку не все калькуляторы могут извлекать такие корни.

Образцовое решение

Сначала для удобства представим члены заданного ряда в виде степеней с дробными показателями:

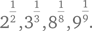
Эффективной стратегией здесь является организация данных так, чтобы было легко сравнивать.

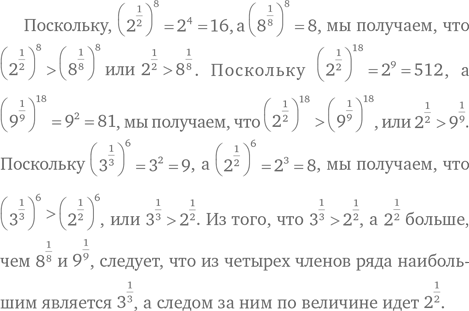
Задача 7.12

У класса есть возможность принять участие в походе. Желающих оказалось пять человек, а свободных мест — всего три. В числе желающих — Аманда, Билл, Кэрол, Дэн и Эван. Учитель взял пять листочков бумаги, каждый с именем одного из желающих, положил их в шляпу и вытащил три листочка наугад. Какова вероятность того, что Аманда, Билл и Кэрол попадут в число участников похода?

Обычный подход

Сначала определим, сколько вариантов выбора может существовать. Порядок не имеет значения, поэтому это комбинаторная задача. Из пяти листочков выбирают по три за раз:

Поскольку Аманда, Билл и Кэрол могут выпасть только один раз, ответ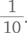

Образцовое решение

Если вы не знакомы с комбинаторными вычислениями, то можете воспользоваться стратегией организации данных. Составим перечень всех возможных сочетаний имен в любом порядке:

Существует 10 возможных вариантов выбора трех человек. Только один из них, а именно ABC, удовлетворяет условиям задачи. Таким образом, правильным ответом будет один из 10, или