Глава II. Принципы нечеткой логики

Неудивительно, что средства нашего языка не способны описать процессы, происходящие внутри атомов, поскольку наш язык был изобретен для описания событий повседневной жизни, а они, как известно, состоят только из процессов с участием чрезвычайно большого количества атомов.

Вернер Гейнзберг

Основной принцип нечеткой логики гласит: все зависит от степени и познается в сравнении. В данной книге нечеткая логика, одно из величайших достижений математики XX века, рассматривается через призму человеческой жизни и окружающего нас мира, а также мировоззрения. Некоторые вещи никогда не будут нечеткими, в основном это вещи, происходящие из мира математики. В этом мире Бог или же человек не оставили места нечеткости. Мы соглашаемся с утверждением, что 2 + 2 = 4, но когда возвращаемся из мира математики в реальный мир, окружающий нас, балом правит нечеткость. Она стирает рамки, размывает границы, словно мы разрезаем границы Вселенной на кусочки тупым ножом.

У нечеткости есть свое имя в науке – поливалентность, то есть способность образовывать множественные различные связи. Антонимом здесь послужит двухвалентность, подразумевающая лишь два варианта ответа на вопрос либо однозначное утверждение о каком-либо факте: оно может быть только истинно или исключительно ложно. Как уже было упомянуто выше, нечеткость подразумевает многовалентность, иными словами, широкий спектр возможностей и вероятных ответов и комментариев относительно какого-либо утверждения вместо лишь сухих двух. Это означает, что нечеткая логика обладает всем диапазоном оттенков серого цвета для описания мира вместо всего лишь двух, черного и белого.

Ученые в 20–30-х годах прошлого века впервые разработали многозначную логику для решения принципа неопределенности Гейзенберга в квантовой механике, о чем мы поговорим ниже. Принцип неопределенности Гейзенберга гласит: чем точнее измеряется одна характеристика частицы, тем менее точно можно измерить вторую. Принцип предполагает, что мы действительно имеем дело с трехзначной логикой: утверждения, которые являются истинными, ложными или неопределенными.

Польский логик Ян Лукасевич нарезал среднюю «неопределенную» составляющую на несколько частей и придумал многозначную логику. Термин «нечеткая логика» прочно вошел в научный язык. До тех пор логики, такие как Бертран Рассел, для описания многозначности использовали термин «неопределенность». В 1937 году квантовый философ Макс Блэк опубликовал статью о неопределенных множествах (о том, что мы теперь называем нечеткими множествами). Мир науки и философии проигнорировал статью Блэка, иначе мы могли бы теперь обсуждать историю смутной, а не нечеткой логики.

В 1965 году нечеткая логика появилась в работах Лотфи Заде, профессора технических наук Калифорнийского университета. В своих работах Заде обращался к термину многозначной логики, введенному Лукасевичем, перечисляя и рассматривая множества объектов и предметов, – аналогично примеру со множеством людей, удовлетворенных и неудовлетворенных своей работой. Лотфи Заде предложил миру науки того времени нечеткую логику, чтобы связать математику с интуитивным способом, которым люди разговаривают, думают и взаимодействуют с миром. Работа Заде стала основополагающей в возникновении теории нечетких множеств.

Введение термина «нечеткости» спровоцировало шквал научного гнева, обрушившегося на его создателя, а точнее говоря, с появлением данного термина появился целый ряд научных проблем. Государство отказывалось финансировать исследования в области «нечеткости»; газеты и журналы не хотели публиковать статьи на эту тему; университеты не поощряли исследователей нечеткости и их научные работы; можно сказать, что в то время небольшое сообщество ученых, пропагандирующих учение о нечеткости, ушло в подполье. Но, тем не менее, со временем оно обрело силу, стремление развиваться и стало полноценным учением. Условия, в которых оно развивалось, лишь укрепили его постулаты.

Нечеткая логика не достигла успеха на своем поприще в университетах. Она скорее преуспела на коммерческом рынке и перескочила философские возражения западных ученых. Нечеткий принцип возник с попыток западной культуры отрицать его, игнорировать, опровергать и всячески бороться с возможностью его развития. Наши рассуждения всегда остаются нечеткими. Более того, мы можем обеспечить бытовые приборы некоторым интеллектом исходя из принципов нечеткости и используя нечеткие концепции. Безусловно, медленное распространение нечеткости по миру насторожило многих ученых и в некоторой степени напугало их, поскольку ученые того времени были уверены, что в основе работы бытовой техники и прочих машин заложена строгая черно-белая логика и математические постулаты и принципы. Этот процесс спровоцировал новые обсуждения искусственного интеллекта. В данной книге мы рассмотрим нечеткий принцип в разных вариациях: от Древней Греции и Индии до современной Японии и не только: умная бытовая техника и инновационное оружие будущего встретятся на стыке науки и инженерии.

Итак, теперь мы знаем, что одним из первых логиков, предложивших в 1930 году вариант многозначной логической системы, отличающийся от классической бинарной логики, был польский математик Ян Лукасевич. В трехзначной логике Лукасевича использовалась три возможных истинных значения: «ложь», «истина», «возможность». В качестве высказываний с истинностным значением «возможно» могли выступать такие, которые относились к некоторому моменту времени в будущем. Затем термин «нечеткая логика» был введен профессором Лотфи Заде в работе «Нечеткие множества» в журнале «Информатика и управление». Предметом нечеткой логики стало исследование рассуждений в условиях нечеткости, размытости, сходных с обычными рассуждениями, и их применение в вычислительных системах. Лотфи Заде по праву считается отцом нечеткой логики. Мировая наука действительно изменилась после его открытий: на сегодняшний день нечеткая логика широко применяется в производстве бытовой техники, управлении транспортными средствами и промышленными процессами. Помимо прочего, нечеткая логика применяется и в политике, и в экономике. Вопреки аристотелевскому положению, которое может быть верным или неверным, Заде доказал, что степень истинности любого утверждения принимает непрерывные значения между истинностью и ложностью. Заде сделал открытие, которое противоречит теории великого Аристотеля, призывает видеть и воспринимать мир более красочным. Теория нечетких множеств, представленная Заде, стала новой вехой в информационных технологиях.

Но теория была скептически воспринята не только в США, но и в научных кругах во всем остальном мире. Причиной этому послужило противоречие этой теории логике самого Аристотеля, которой люди руководствовались на протяжении многих веков. Аристотель всегда считался основоположником классической теории логики. Однако классическая логика имеет большой недостаток – ее применение бесполезно в случае описания мышления человека. Проблема заключается в том, что возможно оперировать только двумя утверждениями: истина и ложь, других средних значений между ними не существует. Двоичная логика, которая, сравнивая два числа, определяет состояние системы, также признает только единицы и нули. В случае с вычислительными машинами не возникает проблем, но описание окружающего мира исключительно двумя понятиями представляет собой практически нерешаемую задачу. Нечеткая логика в силах справиться с ней.

Пожалуй, то, что теория о нечеткой логике получила всемирное признание, является заслугой Лотфи Заде. Благодаря Заде нечеткая логика с каждым годом привлекает все большее число исследователей из разных научных областей. В настоящее время нечеткой логикой во всем мире занимаются тысячи ученых и инженеров, по этой тематике опубликованы сотни книг, десятки тысяч статей, издается более 40 научных журналов по нечеткой логике и мягким вычислениям, механизмы нечеткой логики реализованы в сотнях прикладных систем.

В данной книге мы рассматриваем прошлое нечеткости, ее настоящее и будущее. Когда мы обращались к прошлому нечеткости, мы рассматривали исторические корни и происхождение нечеткости, начиная путь с логики Аристотеля. Изучая настоящее нечеткости, мы рассматриваем нечеткие множества и системы и то, как они получили признание в США и Японии. Будущее нечеткости предполагает то, каким образом нечеткая логика и высокопотенциальный интеллект машин может сказаться на жизни общества и повлиять на него в ближайшем и отдаленном будущем.

Двухвалентность и многозначность

Двухвалентности присуще делать выбор в пользу простоты, нежели точности. Черное и белое, истина или ложность очень удобны для суждения в математике и компьютерном программировании. Но, как бы там ни было, двухвалентность требует вовлечения оттенков серого и округления на определенном этапе рассуждений: достаточно вспомнить вопрос о том, кто из присутствующих в аудитории был доволен своей работой.

Информационная эпоха опирается на двухвалентность, потому что она опирается на «цифровую революцию» в обработке сигналов и микропроцессорных компьютерных чипах. Мы измеряем величины – звук, кровяное давление, интенсивность света, напряжение, температуру, интенсивность землетрясений – которые со временем плавно меняются. Мы должны пробовать округлять эти сигналы для того, чтобы передать их двоичному компьютерному интеллекту.

Мы можем рассматривать временной сигнал как кривую, колеблющуюся вверх и вниз, влево и вправо.

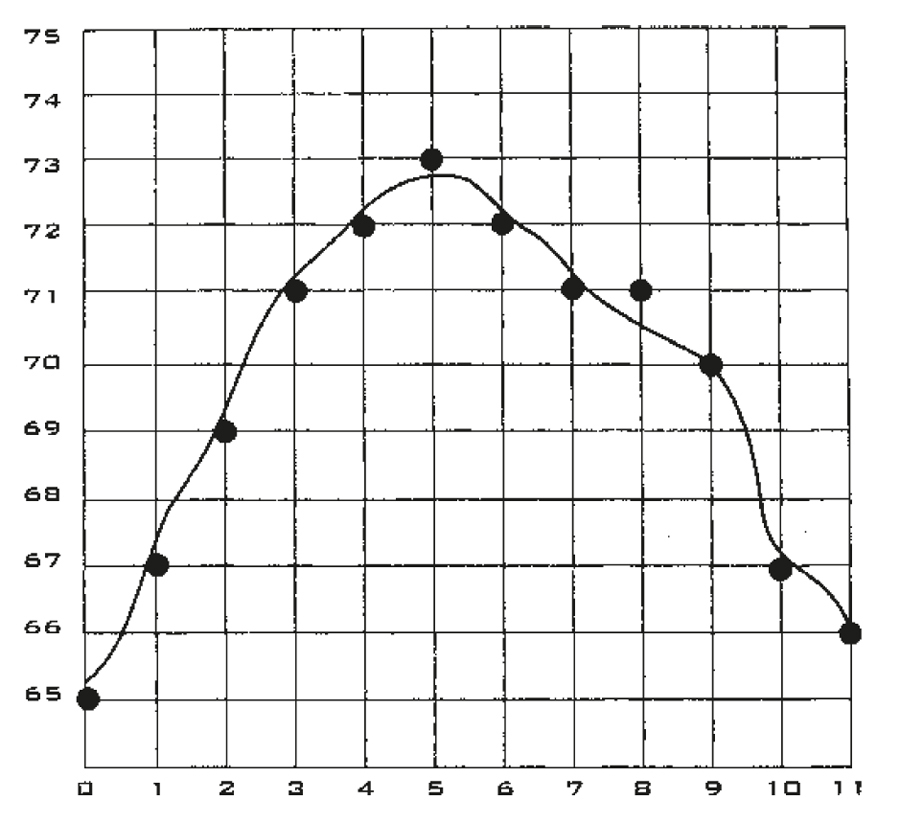
Ученые написали тысячи работ о том, как же изображать временную кривую, результатом явилось то, что чем больше отрезков времени возможно отобразить на кривой – тем лучше и информативнее. Оцифровка разрезает вертикальную линию на набор чисел. Здесь система округляет сигнал до ближайшего нарезанного значения. Затем система отбрасывает реальность и сохраняет только оцифрованные числа (черные точки в сетке) и преобразует каждое число в уникальный список. Остальное – это высокоскоростное число и мир компактных лазерных дисков, сотовых телефонов, факсимильных аппаратов, спецэффектов в фильмах и новых изображений Нептуна и Венеры.

Западная культура теперь видит двоичную, бинарную точность как часть научного метода. Цифровая революция словно оцифровывает наши умы. Представьте себе компьютер, который на какой-либо заданный ему вопрос дал бы ответ: более или менее. Скорее всего в данном случае мы бы решили, что компьютер просто-напросто запрограммирован ученым в белом халате таким образом, чтобы он мог разговаривать с нами равносильно тому, как общаются друг с другом люди. Мы бы точно не подумали, что компьютер действительно имеет в виду то, что он дал нам верный, на его взгляд, ответ на заданный нами вопрос.

Двоичная логика Аристотеля опирается на наши двухвалентные инстинкты. Мы ожидаем, что каждое хорошо и твердо сформулированное утверждение будет истинно или ложно, но не более истинно или более ложно. Этот строгий закон прослеживается и в нашем языке, и в наших мыслях и суждениях. Религиозный философ Серен Кьеркегор назвал книгу, написанную им в 1843 году «Или-или», в ней человек рассмотрен как космический раб двоичного выбора – быть или не быть, делать или не делать. В трактате «Или-или» представлена диалектика человеческой экзистенции. В каждой философии или религии существует зло, с которым она борется и стремится искоренить. Зло двузначности – это логическое противостояние истинности и ложности фактов.

В двухвалентной логике противоречие подразумевает все. Оно позволяет доказать или же опровергнуть любое утверждение. Математики трудятся над выдвигаемыми ими аксиомами для того, чтобы они не подразумевали высказываний, которые противоречат друг другу. До сих пор никто не доказал, что аксиомы современной математики не приводят к утверждениям, которые противоречат друг другу. Но в любой момент, даже уже завтра, все может измениться, и рамки современной математики просто-напросто рухнут. Между тем страхи и домыслы в области науки остаются. Именно поэтому в науке мало терпимости ко взглядам, которые допускают противоречия, совпадения между вещами, объектами и неминуемыми фактами. Нечеткая логика противостоит этой нетерпимости. Нечеткость начинается там, где возникают противоречия, где факты в какой-либо, даже самой минимальной степени, противоречат друг другу.

Восточная культура предлагает системы убеждений, которые не базируются на точной бинарной логике и четкости фактов, эта культура предполагает существование противоречий между фактами, Инь и Ян. Задолго до Аристотеля Будда уже размышлял иным путем, не позволяя загнать свои суждения в рамки «или-или». Он хранил благородное молчание, задаваясь бинарными вопросами, например, бесконечна ли Вселенная или же имеет четко очерченные границы.

Современные буддийские монахи дзен обучают медитировать на коанах – коротких вопросах, диалогах, не имеющих логической подоплеки, более доступных интуитивному пониманию: например, как выглядело ваше лицо прежде чем вы родились? Или, как одна рука воспроизводит хлопающий звук при соприкосновении с другой? Иными словами, путем медитации на коанах осуществляется попытка выйти за черно-белые рамки сознания. Даже Мао Цзэдун, китайский государственный и политический деятель XX века, писал работы на тему противоречий.

Давайте снова рассмотрим яблоко, которое, допустим, вы держите в руке, а затем откусываете от него по кусочку. Сначала то, что вы держите в руках, можно на 100 % назвать яблоком, чем оно и будет на самом деле являться. Когда вы откусываете яблоко часть за частью, оно перестает быть яблоком, то есть процент существования яблока падает со 100 % до 0 %, пока вы не съедите его полностью. На протяжении процесса у вас в руках будет находиться лишь 50 % яблока, поскольку половину вы уже съели. Проценты постепенно передают значения яблока как целого предмета до полного его отсутствия. Если мы нарисуем график, соответственно которому яблоко будет исчезать, то обозначим проценты линиями, где каждая линия будет занимать конкретное место относительно 100 % и 0 %. Эти линии будут отображать конфликт и противостояние между двухвалентностью и нечеткостью. Нечеткость или многовалентность будет содержать в себе информацию о процессе между строк. Когда в стакане не много воды, мы определяем его заполненность определенными рамками, – например, говорим, что стакан полон на 5 % или 10 %, тем самым сводя количество воды в стакане к определенной отметке. На деле же мы смотрим, к какой из отметок, 5 % или 10 %, находится ближе уровень воды, и округляем уровень воды до этой цифры. Здесь и кроется нечеткость.

Зачастую округление подходит, чтобы сгладить небольшие углы, когда дело касается цифр. Но что произойдет в случае, если мы решим округлить средние значения? В какую сторону и до какого значения нам стоит округлить 50 % – до 0 % или же до 100 %? Вопрос будет заключаться уже не в том, наполовину пуст стакан или же наполовину полон, а в том, пуст или полон рассматриваемый нами стакан в целом. Взаимодействие и использование средних значений в современной математике имеет отсылку к так называемым парадоксам. Математики применяют термин парадокс к среднему значению для того, чтобы делать свои предположения о пограничных случаях и исключениях. Фактически они возникают на основах бивалентной математики и логики. Математический парадокс – это такое высказывание, которое в теории может быть равно доказано и как истина, и как ложь. То есть, парадокс – это рассуждение, доказывающее как истинность, так и ложность некоторого суждения, иными словами, доказывающее как само суждение, так и его отрицание.

Одним из широко известных является теоретико-множественный «Парадокс брадобрея», открытый Бертраном Расселом в начале XX столетия. Рассел сформулировал известный парадокс о множестве всех множеств, которые не являются элементами самого себя. Суть парадокса заключается в противоречии при рассмотрении вопроса о принадлежности самому себе множества всех множеств. Его изложение имеет несколько различных формулировок. Одна из них такова:

«В полку служил парикмахер, которого также называли брадобреем. Однажды командир приказал ему побрить только тех, кто не бреется сам. Многие солдаты умели бриться сами, соответственно, брадобрею нужно было брить только тех, кто сам не умел. Тогда у брадобрея возник вопрос: брить ли ему самого себя? Ведь если он будет бриться, то нарушит приказ командира не брить тех, кто бреется сам. Брадобрей решил, что брить себя он не будет, но тогда понял, что если он сам себя брить не будет, то окажется, что он сам не бреется, и по приказу командира он должен все-таки себя побрить».

Рассмотрим подробнее. Если брадобрей бреется сам, то он принадлежит ко множеству тех, кто бреется сам. Но в заявлении утверждается, что брадобрей никогда не бреет тех, кто входит в это множество. Следовательно, наш брадобрей не может брить самого себя. Если же его бреет кто-нибудь другой, то он принадлежит к числу тех, кто не бреется сам. Но в заявлении сказано, что он бреет всех, кто не бреется сам. Следовательно, получается, никто другой не может брить этого брадобрея. Похоже, что его не может брить никто! Бертран Рассел предложил парадокс брадобрея, чтобы облечь в более наглядную форму знаменитый парадокс, обнаруженный им в теории множеств. Некие математические конструкции приводят к множествам, которые включают себя в качестве одного из своих членов. Например, множество, содержащее все, что не является яблоком, само не является яблоками и, следовательно, не должно содержать себя в качестве одного из членов. Рассмотрим теперь множество всех множеств, не содержащих себя в качестве одного из членов. Получается, что противоречия избежать невозможно. Любой ответ приводит к противоречию.

Нечеткая интерпретация рассматривает полупустой стакан и парикмахера-брадобрея как усредненные явления. Утверждения о них и возможные заявления, которые описывают их, являются «полуправдами». Они правдивы и действительны на 50 %, а не на 100 % или же на 0 %. Если мы будем настаивать на 100 %-ной истине заполненности стакана или парикмахерской деятельности брадобрея, то мы просто-напросто будем иметь дело с двухвалентным парадоксом. Именно это мы и видим на примере стакана, который заполнен наполовину.

За перетягиванием каната между двухвалентностью и многовариантностью лежит уравнение. Двухвалентность гласит, что уравнения не существует или же оно не имеет логического смысла. Многозначность считает, что оно существует в некоторой степени. В крайних случаях оно существует в полной мере или же, наоборот, совсем не существует. Поскольку редакторы исключают подобные уравнения из книг, подобно тому как садовники выкорчевывают сорняки из своих цветочных садов, уравнение, которое мы рассмотрим ниже, пожалуй, центральное уравнение данной книги и нечеткой логики, будет называться уравнение Инь-Ян. Несомненно, для ученых, логиков и математиков оно покажется смешным, но тем не менее вот оно:

А = не А

Как вы уже догадались, это – противостояние фактов в форме уравнения. Вместо того чтобы написать «Факт А и одновременно не факт А», знак равенства уравновешивает две пропорции по обе его стороны. Таким образом, парадокс двухвалентного рассуждения сводится к уравнению Инь-Ян: полупустая чаша подразумевает, что чаша наполовину заполнена, и наоборот. Мы можем нарисовать картину уравнения Инь-Ян в действии, точнее, последовательность изображений, где уравнение Инь и Ян будут взаимодействовать в разных степенях. Вспомните диаграмму Венна, в которой дано схематичное изображение всех возможных отношений нескольких подмножеств универсального множества. На диаграммах Венна универсальное множество изображается множеством точек некоторого прямоугольника, в котором располагаются в виде фигур все остальные рассматриваемые множества: предположим, что мы разрезаем прямоугольник или коробку на две части: часть А и часть не А, набор А и набор не А. Мы разделили линией ящик яблок на красные и не красные яблоки. Таким образом, мы проводим четкую границу между двумя частями яблок: А и не А.

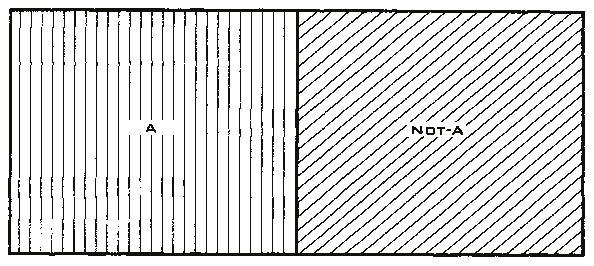
Это двухвалентный случай, черно-белый мир математики и Аристотеля. Наше уравнение Инь-Ян здесь вообще неприменимо. Более того, оно имеет абсолютно нулевую степень. Существуют только точные, четко очерченные границы. Теперь предположим, что некоторые яблоки не полностью красные – на них есть оранжевые, розовые или зеленые полосы. Если мы попросим продавца фруктов распаковать ящик яблок и разделить его на две части – красные и яблоки, которые красными не являются, он может сформировать не только две части яблок, но отложить и третью часть – яблоки, которые не будут принадлежать ни к одной из двух вышеупомянутых категорий. Яблоки из третьей части будут в некоторой степени красными и в некоторой степени зелеными или розовыми. Именно эту третью часть продавцам фруктов трудно классифицировать, и они таким образом нарушают закон Аристотеля: либо – либо.

Теперь предположим, что продавец распаковывает новую коробку яблок. На этот раз каждое яблоко настолько же не красное, насколько красное. Мы не знаем, как продавец измеряет красноту яблок, пока он раскладывает яблоки по разным частям. Получается, что все яблоки попадут в третью гору яблок и, если мы захотим изобразить это на диаграмме Венна, она будет выглядеть уже по-другому.

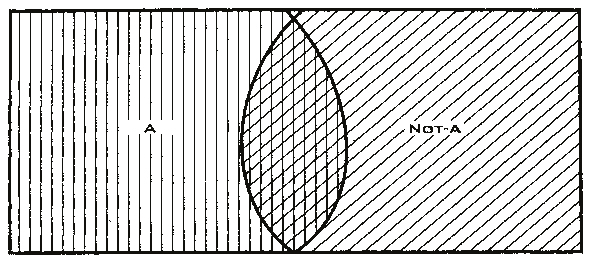
Помимо этого, можно изобразить диаграмму Венна, где две части яблок будут идентичны друг другу и, соответственно, равны друг другу.

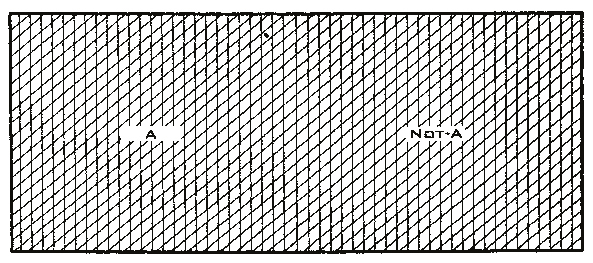
Тогда наше уравнение Инь-Ян будет точным на все 100 %: А = не А, поскольку мы не можем отличить части яблок.

Эти три примера, три нечетких диаграммы Венна еще раз показывают нам, что черное и белое – особенные случаи серого и что многозначность сводится к бивалентности в крайних случаях. В жизни, как и в диаграммах Венна, мы чаще обмениваем нечеткость на простоту двузначности.

В поисках компромисса между нечеткостью и двузначностью ученые искали картину которая могла бы его обрисовать. И эта картина была найдена на примере кубика Рубика. Цветные маленькие квадраты не были частью этой картины, хотя являлись частью более сложной картины нечетких систем. Кубик Рубика выглядит как трехмерный нечеткий куб. Любая из шести граней кубика Рубика выглядит как двумерный куб или сплошной квадрат – двумерный нечеткий куб. Любое из двенадцати ребер кубика Рубика выглядит как одномерный куб или прямая линия над одномерным нечетким кубом.

Если по углам куба лежат бивалентные множества, то что же находится внутри? Нечеткие или многозначные множества. Итак, по углам куба лежит двухвалентность, многозначность же находится в других плоскостях. Логика Аристотеля правит на гранях нечеткого куба, в редком случае черно-белых опций среди серых опций. Логика и мышление Будды правит там, где нет граней и углов куба. Логика Будды правит повсюду внутри этого куба. Можно сказать, что она полностью, на 100 % действует в средних значениях, в середине самого куба, где мы видим наше уравнение Инь-Ян. Читателю эта картина может комично представиться в виде маленьких фигурок Будды и Аристотеля, находящихся по обе стороны кубика. Куб сам по себе является своего рода парадоксом: как бы ни старались ученые, у них никогда не получится привести то, что внутри этого куба, к черно-белым рамкам, ребрам этого самого куба. Невозможно одновремено наполовину заполнить и опустошить стакан с водой. Пожалуй, средние значения отклонений – своеобразная черная дыра в теории множеств.

Больше информации – больше нечеткости

Информация помогает нам представить мир. Каждую секунду наши глаза передают нашему мозгу миллионы битов информации. Наши умы питаются посредством газет, телешоу, телефонных звонков, писем и даже сплетен. Мы расширяем наши ощущения с помощью микроскопов, контактных линз, биноклей, термометров, сканеров, телескопов и сотен других устройств, которые помогают нам преобразовать мир в информацию и воспринимать таким образом. Каждая новая система координат меняет наш разум. Внутри нашего мозга они влияют на то, как действуют наши мозговые клетки или нейроны, синапсы, по которым нервные импульсы передаются между двумя клетками. По мере получения дополнительной информации мы получаем более точную картину мира. Мы получаем более четкое представление о фактах. Но влияет ли все это каким-либо образом на нечеткость фактов?

Предположим, что Джону исполнилось тридцать лет. Стал ли Джон старым? Да или нет? Он молод? Да или нет? Добавьте немного информации. Уточните возраст Джона. Скажем, мы знаем, что Джону исполнилось 30 лет в конкретный день (уточните день его рождения). Так, получается, что Джон старше или моложе в зависимости от того, когда именно ему исполнилось 30. Что говорит нам точная информация о возрасте Джона? Она говорит нам, что Джон будет старше, когда ему исполнится 35 лет, т. е. в этом случае он будет старше, чем сейчас. Это говорит нам о том, что вопросы, стар он или молод, вопросы именно о старости и о молодости, являются вопросами степени. Это нечеткие понятия – старые и молодые – для нечетких подмножеств населения.

Все сводится к следующему: как и где мы рисуем линию? Этот вопрос преследует черно-белые рассуждения о мире серого. Правительство США утверждает, что совершеннолетие начинается с первой секунды восемнадцатилетия. Правительство разграничивает людей четкой линией. Мы можем представить ее как воображаемую линию, которая разбивает детей и взрослых по шкале лет.

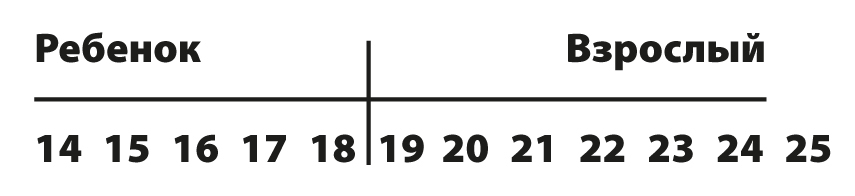
Мы можем рисовать разные линии в разное время в возрасте до и после 18 лет, но не можем обозначить их предельно четко, веско обосновав их. Мы знаем лишь и с уверенностью можем утверждать, что 14-летняя девушка не является совершеннолетней и будет гораздо младше той, которой 25 лет и которую уж точно можно назвать взрослой. Мы также знаем, что, в соответствии с нечеткой концепцией, взрослость наступает с возрастом. Таким образом, нечеткий принцип рассматривает взрослых как нечеткое понятие и рисует его как кривую, а не линию.

Попробуем простым языком объяснить, что такое теория нечеткой логики на примере такого понятия как молодость. Казалось бы, возраст легче всего связать с числами и математикой. Но не все так просто. Так, если установить некий формальный возрастной интервал (скажем, от 16 до 30 лет) и оставаться в рамках классической двоичной логики, допускающей только «да» или «нет», то результат будет противоречить логике человеческой: если ваш возраст равен «30 лет + 1 день», то вы сразу выпадаете из категории «молодой».

Нечеткая теория рисует кривую между противоположностями: между А и не А. Больше информации, больше «фактов» помогают нам нарисовать кривую. Если у нас будет достаточно информации, мы можем превратить наши смутные представления о старых и молодых в кривые с нечетким множеством.

Чем большим количеством информации мы располагаем, тем рельефнее и реалистичнее кривая. Раскол между предметом и тем, чем он не является, усложняет рассмотрение в том случае, если вещь относительна. Допустим, мы рассматриваем грань между искусством и тем, что искусством не является. Поможет ли нам дополнительная информация понять, являются ли живопись и стихи искусством? В конце концов, раскол – это, пожалуй, «призыв к суду». Объекты в определенной степени являются искусством или им не являются – в зависимости от вкуса, традиции и прихотей. В итоге продавцы, покупатели и критики в сфере искусства оценивают картины, рисунки и скульптуры в соответствии с тем, что они видят в качестве объектов красоты.

Красота одновременно нечетка и относительна. Это зависит от изучающего ее и культуры. Похожие картины, мелодии или сюжетные линии и фразы могут стать началом культурной тенденции или же причиной обвинения в плагиате. Популярные исполнители, артисты и комедианты преуспевают в размывании границ между красотой и развлечением, между пониманием и абсурдностью, между искусством и неуточненным его определением. Красота предмета – не только в глазах смотрящего.

Юридические решения также нечетки и относительны. Масштабы правосудия варьируют в разных степенях в зависимости от ситуации. Судьи часто осуждают лиц, которые совершают преступления по неосторожности и оправдывают тех, кто совершил злодеяния намеренно. Судьи, ученые-юристы и все остальные ищут границы между личной свободой и государственным контролем, между человеком и государством, выбором и командованием. Шутки имеют оттенки оскорбления, клеветы или притеснения. Вы можете владеть землей, на которой построен и стоит ваш дом, но владеете ли вы воздушным пространством над вашим домом? Принадлежат ли вам десятки радио- и телевизионных сигналов, которые прямо сейчас распространяются на ваше тело? Кто владеет океанами, луной и солнцем? А что, если мы выкопаем древние свидетельства о принадлежности собственности нашей планеты Земля инопланетянам, которые только что продали планету другой расе или посеяли здесь жизнь?

Правовые понятия различаются между культурами и внутри них. Значительное увеличение количества информации и данных в XX веке не помогло четко прочертить линии между справедливостью и несправедливостью, истиной и ложью, правильным и неправильным, частным и общественным, общим и частным. Информация будет увеличиваться и расширяться. Вместо того чтобы упрощать юридические решения, дополнительная информация увеличивает путаницу в законодательном поле. Это лишь углубляет юридическую трясину. Чем больше точности – тем больше информации. Чем больше информации – тем больше нечеткости.

Больше информации означает больше фактов. Более подробная информация будет лучше описывать факты. Это даст нам более четкую картину фактов под разными углами. Но нечеткость, похоже, обещает быть постоянной частью этих картин. Во многих отношениях будущее выглядит размыто и странно.

Нечеткость в развитии интеллекта машин

Мы уже говорили о чрезвычайном успехе и влиянии нечетких систем на технику. Сложно переоценить значение нечеткой логики при изготовлении товаров различных уровней потребления для людей. Речь пойдет об искусственном интеллекте. Искусственный интеллект – это, можно сказать, экспериментальная научная дисциплина, задача которой – воссоздать с помощью искусственных устройств разумные рассуждения и действия технических приборов, призванных служить человеку в повседневной жизни. Искусственный интеллект подразумевает решение компьютером задач, не имеющих явного алгоритмического решения. При этом часто используются «человеческие» способы решения таких задач. Научный аспект искусственного интеллекта касается объяснения работы естественного интеллекта и имитации решения задач человеком. Данная область, именно область искусственного интеллекта, стала развиваться после возникновения компьютеров и на сегодняшний день используется в огромном количестве отраслей, от бытовой техники до управления атомными станциями. Развитие искусственного интеллекта машин идет параллельно с ускорением компьютеров и научным прогрессом.

Возможно, через некоторое время, скажем, несколько десятков лет, искусственный интеллект сможет сравниться с интеллектом живого человека и, вероятно, когда-нибудь сможет превзойти его. Сегодня технологии искусственного интеллекта включают в себя множество различных подходов.

Среди них нейронные сети, работающие на принципах, схожих с работой мозга, которые используются для распознавания речи и рукописного текста, для постановки диагнозов, в финансовых программах. Эволюционные алгоритмы предполагают создание качественно новых программ, их скрещивание, обмен частями и тестирование. Программы, работающие лучше всего, выживают, и через несколько поколений получается наиболее эффективная. Нечеткая логика дает компьютеру возможность работать с объектами из реального мира и их взаимоотношениями. С помощью нечеткой логики компьютер может понять такие термины как «близко», «теплее», «почти» и прочие. Именно поэтому нечеткая логика активно используется в бытовой технике, например кондиционеры и стиральные машины.

Значительная часть используемых сегодня роботов обладает как минимум зачатками искусственного интеллекта. Эти роботы способны ориентироваться в окружающей обстановке и распознавать нужные им объекты. Системы на основе искусственного интеллекта и нечеткой логики управляют промышленными объектами, такими как заводы, атомные станции, транспорт. Крупнейшие финансовые организации используют их для моментального принятия эффективных решений на фондовых и валютных рынках. Искусственный интеллект широко используется в компьютерных играх для создания графики, населения виртуальных миров персонажами с реалистичным и разумным поведением.

В разработке интеллектуальной техники все чаще используются знания по психофизиологии, полученные с помощью наблюдения за поведением животных и людей. В соответствии с этими представлениями формирование тактики поведения осуществляется работой функциональных систем, каждая из которых соответствует некоторому поведенческому акту, сформированному при обучении и включенному в структуру индивидуального опыта.

Инженеры, работающие с техникой в области нечеткости, разрабатывают программное обеспечение и специальные чипы для того, чтобы заставить компьютеры и машины рассуждать так же, как люди, и повлиять на их работоспособность таким образом, чтобы она стала более продуктивной и интеллектуальной. Безусловно, это способствует более легкой работе техники и более легкому обращению с ней. Теперь мы можем программировать системы на английском, японском и многих других языках. Скорее всего, будущие нечеткие системы позволят нам программировать их даже устно, вместо того чтобы нажимать на кнопки. Нечеткие системы изучают огромное количество опыта и различных программ.

Как действуют нечеткие приборы? Нечеткие правила делают отсылку к нечеткому концепту и базируются на утверждении, что если X – это А, то Y – это В. Например, если дорожное движение очень быстрое и непрерывное, то зеленый свет на светофоре должен гореть дольше. Такое рассуждение имеет под собой здравый смысл, не так ли? Правило связывает нечеткие множества непрерывного и долгого. Мы также можем изобразить эти множества посредством кривых. Любое дорожное движение в некоторой степени достаточно быстро и непрерывно, а поток машин постоянно движется; поэтому мы можем сделать так, чтобы зеленый свет на светофоре горел дольше относительно конкретной степени. Комбинации плотности, скорости дорожного движения и времени зеленого светофора бесконечны. Тем не менее, одно правило объединяет их – правило интеллекта машины, управляющей процессом, в данном случае интеллекта светофора на автомобильной трассе.

Нечеткие системы хранят в себе десятки, сотни или даже тысячи этих правил, основанных на здравом смысле. Каждая новая часть данных активирует нечеткие правила до некоторой степени. Затем нечеткая система объединяет данные и выдает окончательный вывод или ответ. На нечетком чипе это параллельное рассуждение занимает тысячи или миллионы раз в секунду. Мы подсчитываем количество логичных выводов в секунду.

Высокоскоростные нечеткие системы умны. Сегодня в Японии они контролируют метрополитен и стабилизируют вертолеты лучше, чем это способны сделать люди. Нечеткость в их системах обеспечивает надежный и мягкий контроль. Это сокращает отрывистые перерегулирования и несостоятельность старых систем математического контроля: кондиционер, который продуцирует слишком холодный или слишком теплый воздух, камера, снимающая нечеткие изображения. Скоро у нас будут нечеткие устройства в домах, офисах, автомобилях и самолетах. Возможно, мы не знаем этого, и рекламодатели могут не вдаваться в подробности, что это именно нечеткие приборы бытовой техники, основанные на правилах нечеткой логики, но это именно они. Мы будем командовать армиями крошечных высокоскоростных опытных экспертов, которые никогда не ошибаются, не устают и не жалуются.

Сенсорные технологии, новейшие датчики ускоряют нечеткую революцию. Эти крошечные нечеткие эксперты нуждаются в большом количестве данных, и чем быстрее и точнее они получат и обработают их, тем лучше. Современные технологии в бытовой технике не перестают удивлять нас. Нечеткая стиральная машина использует датчики загрузки белья для измерения его объема и текстуры для того, чтобы рассчитать нагрузку и выбрать режим стирки. Помимо этого, такая стиральная машина использует датчик пульсирующего света для определения и отображения загрязненности воды, в которой мы стираем белье. Каждую секунду несколько нечетких правил превращают эти измерения в структуры водного взбалтывания в течение разных промежутков времени. Нечеткие вакуумные пылесосы используют инфракрасные датчики для измерения плотности грязи и текстуры ковра. Данные поступают извне, и определенные правила регулируют мощность всасывания такого пылесоса. Нечеткие телевизоры измеряют относительную яркость, контраст и цвет в каждом кадре телевизионного изображения, а затем адаптируются таким образом, чтобы дать нам более четкую, максимально яркую картину. Когда мы смотрим телевизор, регуляторы настроек немного меняются, как если бы высокоскоростной эксперт наблюдал за экраном и разработал наилучшее сочетание настроек для каждого из 30 или около того изображений, которые мгновенно мигают.

Теория нечеткой логики нашла применение в тысячах систем и устройств. Она используется в производстве фото- и видеокамер, стиральных машин, вакуумных пылесосов, автомобилей, поездов с автоматическим управлением. В Дании на основе нечеткой логики работают цементные заводы. В Европе изготавливаются системы и устройства с нечеткими экспертными системами. Эта теория важна даже для реализации космических программ. В последние годы в Японии, США и Европе было внедрено большое количество патентов, основанных на применении нечеткой логики.

Особенную роль сыграла нечеткая логика для Японии – она помогла продвинуться вперед японским компаниям. Сегодня в Японии более двух тысяч ученых занимаются применением нечеткой логики в производстве – при разработке бытовой техники, электротехнического оборудования. В Японии за научные достижения Лотфи Заде была присуждена высшая награда Honda. Нечеткая логика быстро нашла применение в электронике. Она позволила микропроцессору – электронному «мозгу» – оперировать промежуточными понятиями. Например, не просто «холодно» и «жарко», но еще и «прохладно», «тепло» и «очень тепло». Благодаря этому техника стала умной – она может гибко реагировать на меняющиеся параметры среды и принимать решения из широкого набора вариантов, заложенных в ее память.

В более старых нечетких системах инженер-эксперт устанавливает правила поведения и реагирования для техники. В современных, адаптированных предметах бытовой электроники заключена «мозгоподобная» нейронная сеть, компьютерная система, которая имитирует работу человеческого мозга, обучается, распознает шаблон и генерирует нечеткие правила из данных обучения. Современная нечеткая техника учится на собственном опыте, работая по схеме «получить данные, выработать правила работы». Нейронная система нечетких приборов ведет себя как глаза и уши системы. Она «видит» шаблоны в данных и медленно вырабатывает правила, которые связывают эти шаблоны. Шаблоны – это нечеткие множества, а отношения – нечеткие правила. Нечеткая система использует эти правила для того, чтобы сопоставлять их с шаблонами. Только представьте адаптированный светофор, который функционировал бы как настоящий полицейский! Чем больше данных получает нечеткая техника, тем продуктивнее она работает.

Адаптивные нечеткие системы сделали потрясающий прорыв. Экспертам не нужно рассказывать и объяснять все процессы в деталях, все, что им нужно – просто заложить в технику основы и данные нечеткой логики. Эти данные включают в себя нейронные сети для поиска и настройки правил. Системы сверхинтеллектуальных машин будущего, будь то умные машины, умные ракеты или маленькие умные роботы, могут развить все возможные нечеткие правила своей работы с помощью нейронных сетей. Возможно, в ближайшем будущем компьютеры достигнут вычислительной мощности, достаточной для полной симуляции мозга человека во всей его сложности. Это сделает практически возможной загрузку человеческого сознания в компьютер. Стоит надеяться, что однажды чистый компьютерный разум сравняется по силе с человеческим и даже превзойдет его.

Наука и ученые – не одно и то же

Ученые в своем большинстве в течение долгого времени достаточно критично рассматривали теорию о нечеткости. Тем временем многие потеряли веру в науку. Это стало глубоким разочарованием для тех из нас, кто ранее уже потерял веру в религию и правительство. И наука не стала спасением.

Научная карьера, как и карьера политическая, зависит в равной степени и от маневрирования внутри нее, и от исследований и стремления к истине. Не многие начинающие ученые знают об этом, когда встают на свой тернистый путь, но, тем не менее, вскоре соглашаются с этим.

Пожалуй, одним из самых сложных открытий, с которым можно столкнуться на пути исследования нечеткого, станет то, что современная наука не приветствует качественно новых идей. И кроме этого, наука допускает ошибки даже на очевидном уровне логики и математики.

Наука предпочитает небольшие шаги большим творческим прыжкам. Модемная наука часто ведет себя относительно новых идей ничуть не лучше, чем католическая церковь вела себя, когда вынуждала Галилея отказаться от своей веры в то, что Земля вращается вокруг Солнца. В отличие от церкви современная двухвалентная наука не претендует на обладание всеми знаниями. Но она утверждает, что придерживается единственного пути к знанию. И следовать ему она предпочитает черно-белым путем логики. Наука полагала, что бивалентность истинна, и поэтому не считала, что нечеткость в какой-то мере научна.

Изучив историю развития нечеткой логики и ее идеи, можно сделать еще одно открытие: наука и ученые, занимающиеся ею – отнюдь не одно и то же. Предмет, которым оперирует и на котором концентрируется наука, – это знание. Предмет же, на котором концентрируются ученые – это их репутация.

В какой-то степени каждый ученый преследует влияние, силу и славу. Ученые уникальны в своем стремлении к ним, по крайней мере, по двум причинам. Во-первых, их ориентир – репутация. Во-вторых, они не отвечают перед вышестоящей властью, им просто-напросто не перед кем отчитываться. Институт науки предоставляет ученым средства для личных целей и получения славы и могущества, а они тренируют большую часть молодежи, принадлежащей к научным кругам, таким образом, чтобы самим стать полноправными членами этого института. Если все идет хорошо, ученые выстраивают себе крепкую, сильную и стабильную репутацию и оставляют за собой продукт науки и знаний.

Они оставляют наследие: журналы, учебники, монографии, материалы конференций, программное обеспечение и даже новые аппаратные устройства. Они получают профессиональные награды, крепко пожимают друг другу руки после речей, получают, помимо прочего, гонорары, призовые деньги, акции совета директоров, и, что самое главное, они получают славу и почет за свои достижения.

Но в науку пришла нечеткая логика. Она расширила двоичную математику, лежащую в основе науки. Это помогло решить проблему несоответствия, позволив нарисовать серые картины серого мира. Как будет упомянуто в следующей главе, нечеткость привела древние и неопределенные понятия «случайность» и «вероятность» к естественным отношениям, которые существуют между множествами. Нечеткая логика внесла свой вклад в интеллект машин, показывая нам, как человечество может заставить машины рассуждать практически также, как люди, рассуждать со здравым смыслом, извлеченным из опыта; иными словами, нечеткая логика качественно подняла машинный интеллект. Во многих случаях нечеткая логика достигла этих высот ценой коллективной репутации десятков тысяч живых и почивших ученых, которые отстаивали двухвалентную теорию. На сегодняшний день большинство надежд возлагается на современных ученых и инженеров.

В прошлом веке Джон Стюарт Милль, британский философ, социолог, экономист и политический деятель, отметил, что новые идеи всегда проходят через три этапа отрицания. Во-первых, они ошибочны. Во-вторых, они, как правило, идут вразрез с религией. И в-третьих, это те же самые истины, старые новости, тривиальный здравый смысл, и мы все поразмыслили бы над ними, если бы у нас было время, деньги и достаточный интерес. Нечеткая логика, связанная с быстрыми темпами изменения информации в обществе, переходит от первого этапа к третьему На Западе нечеткая теория лежит между первой и второй фазой. Большинство ученых все еще нападают на нее как на противоречащую двухвалентной научной вере. Помимо этого, еще и коммерческий успех нечеткой бытовой техники усугубил проблему. На Дальнем Востоке дело обстоит совершенно по-другому: нечеткая теория продвинулась сразу почти до третьего этапа. Там возражения против нечеткой логики имеют больше общего с техническими, чем философскими вопросами: ценность экспертных знаний, наличие научных данных, простота разработки программного обеспечения, скорость компьютерного чипа, точность данных датчиков. В корне нечеткая логика или многозначность есть мировоззрение или идеология. Бивалентность – тоже идеология, и именно в этом заключается конфликт.

Научные идеологии сталкиваются и на политической арене. Зачастую эта тема неприятна людям, но, тем не менее, о ней кто-то должен говорить. История нечеткой логики пронизана политикой, несмотря на то, что многие могут не понимать этого. Человек, как сказал Аристотель, является политическим животным. Политика не контролируется, потому что как ученые, так и исследователи задрапировали ученых с помощью мантии искателя истины и щита специализированных знаний.

Прессе редко удается проникнуть за этот щит или приоткрыть научную мантию, закрывающую истину. Даже если ей и удается это сделать, ее представители не знают, как перемещаться по технической тематике и не знают, кому доверить спор или конкретный вопрос. Таким образом, пресса подчиняется неназванному «большинству» ученых и печатает мнения некоторых из них, а затем и вовсе забрасывает тему. Вспомните, сколько часовых телепрограмм вам доводилось видеть на тему управления исследовательскими фондами или, например, мошенничеству в сфере науки?

Каждый день ученые делают выбор из множества альтернатив. Политика стоит за литературными цитатами и упущениями, академическими акциями, правительственными назначениями, контрактами и грантами, адресами конференций и выборами членов комитетов, выбором редакционной коллегии для журналов и книжных рядов, выбором рецензента для технических документов, контрактных предложений и статусом аккредитации университетов. Ученые преследуют самые разные цели, например, такие, как продвижение по работе, статус, повышение, грант, лучшие консультационные задания, награды, назначения, славу, помощь друзьям, просто радость победы.

Ядерное оружие объединило науку и юристов и заставило их встретиться за столом переговоров. В годы появления ядерного оружия было очевидно: власть преобладает над наукой. Большинство ученых, принимающих участие в обсуждении перспектив и нюансов данного вопроса, были физиками и экономистами. Они выдвигали новые возможные варианты политики властям. Конечно же, они не диктовали способы ведения политики, и лишь немногие из этих ученых стали в будущем политиками. Сегодня же все изменилось. Все больше ученых из разных областей помогают государству решать новые проблемы и разрабатывать новые политические решения.

В какой-то степени каждый пункт социальной повестки дня касается мнения ученых и инженеров. Политики финансируют и пересматривают научные исследования, призывают ученых делиться своей точкой зрения с ними, а затем сочиняют правила и законы. Журналисты, со своими телевизионными и печатными прожекторами, совершенно отдаленные от политиков, вынуждены проводить «научные» опросы, чтобы поддержать взгляды политиков, тем самым они помогают формировать общественное мнение.

Возможно, наступит день, когда наука станет доминировать над политикой и властью. Возможно, этот день и не настанет, несмотря на то, что в мире достаточно ученых, которые могли бы преуспеть в этом. Но здесь есть повод обеспокоиться и отнестись к такому возможному исходу настороженно: если ученым присуще не одобрять качественно новые идеи и, помимо этого, они иногда ошибаются, то они могут сделать ошибку в чем угодно и в дальнейшем.