Эту книгу следовало бы написать задолго до изобретения калькулятора и других вычислительных машин, то есть пока они не испортили нашего отношения к числам. Но утешает тот факт, что эту книгу невозможно было написать до появления нашей системы счисления.

Лишь совсем немногие понимают, что наша система счисления — одно из самых полезных изобретений человечества за всю его историю. При помощи простых символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 можно записать какое хочешь число — до бесконечности. А кроме того, они помогают нам решать любые задачи.

Самое гениальное заключается в том, что величина каждой цифры не является понятием постоянным, а зависит от ее позиции по отношению к другим цифрам. Возьмем число 222: цифра справа обозначает количество единиц, цифра посредине — число десятков, а цифра слева — сотен. Среди ученых это называется позиционной нумерацией.

Для многих из нас такая система — нечто само собой разумеющееся, и нам кажется, будто появилась она вместе с человечеством, однако системы счисления не всегда были такими, как сейчас. Впрочем, люди научились считать за десять тысяч лет до того, как у нас в Норвегии растаяли ледники.

Числа и счет были изобретены для того, чтобы решать практические задачи. Когда числа только появились, считать можно было, даже не зная их. Один из наиболее древних примеров того — археологические находки, сделанные в 1937 г. в пещере в Дольни-Вестонице (бывшая Чехословакия). На лучевой кости волка археологи обнаружили 55 насечек, сгруппированных по пять. Согласно теории Жоржа Ифры, французско-марокканского ученого и автора книги «Всемирная история чисел» (Histoire Universelle des Chiffres), охотник наносил насечку на кость каждый раз, когда убивал какого-то зверя. Возможно, убивая волков, медведей и оленей, охотник делал насечки на различных костях. Этот метод используется и по сей день, разница лишь в том, что мы заменили заостренный камешек и кость бумагой и ручкой. Представьте, что вы работаете в лотерейном комитете и ваша задача — проверить, честно ли действуют различные компании, проводящие лотерею. При каждом броске кубика вы делаете отметку. Чтобы не запутаться, при каждом пятом броске вы рисуете черточку над четырьмя предыдущими. Таким образом вы получаете более наглядное представление о том, как распределяются броски.

Еще можно представить фермера, разводящего овец. Со счетом он не очень дружит, поэтому, подсчитывая овец, тоже прибегает к такой системе черточек. Выпуская овцу пастись, он делает насечку на кости, а вечером, загоняя овец, сопоставляет количество насечек с числом вернувшихся овец.

Некоторые первобытные народности обходились вообще без счета. Это доказывает их язык. В отдельных первобытных языках слова, обозначающие количество, ограничиваются тремя — «один», «два» и «много». Число три обозначается как «два плюс один», а все, что больше четырех, называется «много». Иногда такие огромные числа получают название «тьма».

Числа были особенно важны для успешного функционирования человеческого общества. Пример — торговцы, которым необходимо было вести учет товара и назначать цену. В древнем государстве Элам, располагавшемся на территории современного Ирана, мудрецы придумали простую, но очень удобную вычислительную систему. Палочка стала символом единицы, шарик символизировал десятку, а мячик — сотню.

В большинстве культур, в том числе и в нашей, пользуются десятичной системой, то есть состоящей из десяти различных цифр. Мы редко задумываемся, почему сложилось именно так, но ответ поразительно прост: на каждой руке у нас по пять пальцев, а всего их десять. При помощи пальцев люди в свое время и начали считать. А в таком случае что может быть логичнее, чем десятичная система?

Если же вам кажется, будто наша десятичная система — единственная, то вы заблуждаетесь. Ее изобретали много раз, причем в самых разных уголках земного шара (например, евреи, персы, монголы, тибетцы, инки и римляне).

До появления нашей позиционной нумерации одной из наиболее известных систем была римская — ее по-прежнему используют для нумерации столетий. Хотя римские цифры выглядят странновато, эта система относится к простым. Математики называют ее аддитивной, и это означает, что цифры, стоящие рядом, нужно складывать. Положение каждого символа не влияет на его значение. Вертикальная палочка (I) = 1, две вертикальные палочки (II) = 2, а три вертикальные палочки (III) = 3. Если палочек станет чересчур много, легко запутаться, поэтому римляне ввели следующие символы: V = 5, X = 10, L = 50, C = 100, D = 500, а M = 1000. Так же как и при подсчете единиц, можно подсчитать количество десяток, сотен и тысяч. Значит, XXX = 30, а MMM = 3000. И все же римляне придумали одну хитрость. Чтобы сократить количество символов, они составили правило, позволяющее вычитать меньшее число из большего, если меньшее находится перед большим. Поэтому число 4 обозначается как IV (5 ‒ 1), а число 9 — как IX (10 ‒ 1). Получается, что XIV значит 14 (10 + 5 ‒ 1), а XXXIV — 34 (10 + 10 + 10 + 5 ‒ 1).

Если человек родился в 1973 г., то его год рождения можно записать так: MCMLXXIII (1000 + 1000 ‒ 100 + 50 + 10 + 10 + 1 + 1 + 1).

Как мы видим, для вычислений эта система не особенно удобна. Попробуйте-ка умножить XIX на VIII. Ну и как успехи? Зато складывать римские цифры немного проще. Давайте сложим CCCLII и CCXIII. Сначала надо сгруппировать все одинаковые символы. Получится CCCCCLXIIIII. А теперь чуть-чуть упростим. CCCCC = D, а IIIII = V. Значит, CCCLII + CCXIII = DLXV.

Используя правила сложения, римляне не учитывали правило, согласно которому меньшее число перед большим предполагало вычитание. Чтобы правило срабатывало, такие числа, как 9, приходилось записывать не как IX, а как VIIII.

Не все культуры прибегали к десятичной системе счисления. Кто-то предпочитал двадцатеричную — видимо, руководствуясь тем, что у людей десять пальцев на руках и десять на ногах, то есть всего двадцать. Хороший пример — народ майя, который постигла печальная судьба после открытия европейцами Америки в 1492 г.

Их система счисления просто потрясающая, но применять ее тоже, скорее всего, было непросто. Начало простое: одна точка обозначает 1, две точки — 2, а четыре — 4. Число 5 обозначается горизонтальной чертой. Пока все просто и легко. Далее точки располагаются над чертой: 6 представляет собой черту с точкой над ней (5 + 1), а 7 — черту с двумя точками (5 + 2).

Число 10 представляет собой две горизонтальные линии, расположенные друг над другом (5 + 5). 15 — три горизонтальные линии (5 + 5 + 5), а 19 — четыре точки над тремя горизонтальными линиями (5 + 5 + 5 + 4). А вот отсюда начинается веселье! Числа от 20 записываются в два ряда. В верхнем ряду подсчитывается количество двадцаток, а в нижнем — количество единиц. Чтобы написать число 20, поставьте точку в верхнем ряду (это будет означать 1 × 20). Нижняя линия обводится так, чтобы получился майянский символ нуля (он похож на эллипс или на мяч для американского футбола). Что ж, продолжим. 25 выглядит как точка сверху, что означает 1 × 20, и горизонтальная линия снизу, которая, как мы помним, означает 5. Число 59 записывается как две точки сверху (2 × 20 = 40) и четыре точки снизу над тремя горизонтальными линями (3 × 5 + 4 = 19). Как может заметить наблюдательный читатель, 40 плюс 19 равно 59.

Число 305 записывается тремя расположенными друг над другом линиями в верхнем ряду, потому что каждая из линий — это 5, а значит, в сумме они составляют 15. Так как находятся они сверху, нам надо умножить 15 на 20 — так мы получим 300. В нижнем ряду нам надо нарисовать линию, которая соответствует числу 5. В сумме мы получаем 305.

Сейчас все будет еще веселее! Числа больше 400 записываются в три ряда! Допустим, нам надо записать 861. В нижнем ряду ставим точку, которая обозначает единицу. В среднем ряду (там, где у нас двадцатки) ставим три точки, что значит 3 × 20 = 60. В верхнем ряду ставим две точки, и это значит 2 × 20 × 20 = 800.

Поняли принцип? С каждым рядом число увеличивается в 20 раз.

А чтобы сделать все еще сложнее, майя разработали две версии системы счисления — одну для практического использования, а другую для религиозных и астрономических вычислений. Та, которую мы описали выше, — для практического применения. В версии для религиозных и астрономических вычислений цифры в третьем ряду умножались не на 20, а на 18. Такая система более точно соответствовала астрономическому циклу и позволяла предсказывать настроение богов.

В Месопотамии, которую еще называют колыбелью цивилизации, использовалась шестидесятеричная система счисления. Основным числом здесь было 60, а не 10, как в нашей системе. Число 89 записывалось как (1)(29), что означает 1 × 60 + 29 = 89. А число 4568 записывалось так: (1)(16)(8), то есть 1 × 60 × 60 + 16 × 60 + 8 = 4568.

Удивительно, но пережитки шестидесятеричной системы существуют и в современном обществе. Вспомним часы — час делится на 60 минут, а минута — на 60 секунд.

Шестидесятеричная система — не самая простая в мире. Представьте, как выглядела у майя таблица умножения. Если уж нашу таблицу умножения с десятью числами вызубрить непросто, то представьте, каково было заучивать таблицу умножения в шестидесятеричной системе. Вот это по-настоящему нелегко! Поэтому мозгу намного проще пользоваться десятичной системой, а не двадцатеричной или шестидесятеричной.

Однако удобнее всего двенадцатеричная система — она представляет собой упрощенный вариант шестидесятеричной. Раньше число 12 называлось дюжиной, а 12 дюжин — гроссом. Число 12 удобно тем, что оно кратно множеству других чисел (2, 3, 4 и 6), в отличие от 10 (кратно 2 и 5). На практике это означает, что 1/3 будет работать лучше в двенадцатеричной системе, чем в современной десятичной.

Если бы люди были в родстве с птицами, то мы, по всей видимости, выбрали бы восьмеричную систему, потому что тогда у нас было бы всего восемь пальцев. Восьмеричная система состоит из восьми чисел: 0, 1, 2, 3, 4, 5, 6 и 7, а значит, далее следуют 10 (8 в десятичной системе), 11 (9 в десятичной системе) и так далее. Если продолжать в том же духе, то мы увидим, что числу 16 в десятичной системе соответствует число 20 в восьмеричной. Попробуйте сами! Это очень забавно, и играть в такую игру можно с друзьями. С восьмеричной системой у нас было бы меньше сложностей на заре компьютеризации.

Компьютер запоминает информацию благодаря комбинациям нулей и единиц. Других цифр для него не существует. Это означает, что компьютер пользуется двоичной системой. Если бы человечество применяло восьмеричную систему, для того, чтобы представить одну цифру, достаточно было бы комбинации из трех нулей и единиц. Число 0 можно было бы представить как 000, число 1 — как 001, число 2 — как 010. Если еще немного поразмыслить, выходит, что число 7 было бы представлено как 111. К сожалению, люди оказались менее дальновидными. Десятичная система предполагает, что одно число будет представлено комбинацией из четырех нулей и един иц. На первый взгляд, разница невелика — подумаешь, четыре цифры вместо трех, однако на заре компьютеризации, когда внутренняя память была дорогим удовольствием, восьмеричная система значительно удешевила бы процесс.

Современную систему счисления можно во многих отношениях сравнить с изобретением алфавита. Финикийцы заимствовали свой алфавит у семитских народов Синайского полуострова, которые в свою очередь взяли за основу египетские иероглифы. Иероглифы представляют собой сочетание символов и 24 согласных. В основе еврейского и арабского алфавитов лежит финикийская письменность.

Поразительно, что в еврейском алфавите, как и в греческом, каждая буква имеет свое числовое значение. Если сложить числовые значения букв в слове «Яхве», то есть «Бог» получится 26 — число, ставшее для иудеев священным.

Как говорится во вступлении к этой главе, наша система счисления — позиционная. Значение цифры в ней определяется ее позицией в числе. До такого гениального изобретения люди умудрились додуматься всего четыре раза за всю свою историю. Первый раз это произошло в Вавилоне в начале второго тысячелетия до нашей эры, во второй — в Китае незадолго до начала нашей эры, в третий раз эта система появилась в майянской культуре в период между IV и IX в., а в четвертый ее открыли индийские математики.

Но самое великое открытие сделали в Индии. Именно там было изобретено число ноль в том виде, в каком мы знакомы с ним сегодня. Ноль обозначает отсутствие числа. Ни вавилонцы, ни майя воспользоваться нолем не смогли. Вавилонцы никогда не считали ноль числом, а майя не смогли правильно использовать ноль из-за сложности трехуровневой системы. Китайцы стали применять ноль с подачи индусов, которых нам остается лишь поблагодарить за это изобретение. Спасибо тебе, Индия! И еще одна огромная благодарность — арабам, ведь именно они донесли до нас изобретенный индусами ноль. Переход к современной системе счисления занял несколько сотен лет. За это время внешний вид цифр изменился.

В Европе арабские цифры вызвали смешанные чувства. Некоторые европейские математики воспротивились и даже называли пришедшие из арабского мира цифры дьявольским изобретением. Неудивительно, что европейским ученым приходилось в то время нелегко.

Древние египтяне тоже пользовались десятичной системой, но она была не позиционной, различные числа обозначались иероглифами, а способы умножения и деления вызывают восхищение и по сей день.

Для умножения египтяне записывали числа в две колонки. В первой колонке числа начинаются с единицы и удваиваются до тех пор, пока число не приблизится к одному из умножаемых чисел. Во второй колонке записывается второй множитель, который затем с каждой строчкой удваивается.

Допустим, нам надо умножить 38 на 17.

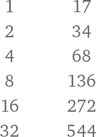
Следующий шаг — найти в левой колонке числа, которые в сумме дают 38.

32 + 4 + 2 = 38

Теперь надо сложить числа в правой колонке напротив чисел 32, 4 и 2.

544 + 68 + 34 = 646

Ну вот — мы с вами умножили числа так, как это было принято в эпоху фараонов: 38 умножить на 17 равно 646.

Деление осуществляется почти по тому же принципу, разве что немного сложнее.

Допустим, нам надо разделить 646 на 17.

Действовать будем так же, как и при умножении. В левой колонке начнем с 1 и будем удваивать числа. Во второй колонке начнем с 17 и будем удваивать числа, пока почти не доберемся до 646.

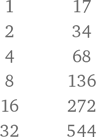
Теперь в правой колонке отыщем числа, сумма которых составляет 646. Это 544 + 68 + 34.

Далее посмотрим, какие числа в левой колонке стоят напротив этих трех чисел, и сложим их.

Вот что получится: 32 + 4 + 2 = 38.

Ну вот мы и совершили настоящий египетский математический подвиг!

646 разделить на 17 равно 38.

Если вас это не впечатлило, то не забывайте, что египтяне осуществляли все эти хитроумные вычисления в те времена, когда наши собственные предки жили в бронзовом веке, а до появления двух великих норвежских математиков — Нильса Абеля и Софуса Ли — оставалось еще много тысячелетий.

Индийские вычислительные методики, сложившиеся во времена, когда у нас в Норвегии только-только начался железный век, были еще эффективнее, а до Европы они добрались благодаря арабским математикам. Метод, который индусы применяли для сложения чисел, очень похож на тот, которому сейчас учат в наших школах. Единственное различие заключается в том, что индусы начинали с самых больших цифр, а числа, которые надо было держать в уме, добавлялись потом. Кроме того, счет велся снизу вверх. Их метод сложения очень похож на тот, которым пользуется мировой чемпион по быстрому счету из предыдущей главы.

В XIII в. арабы придумали сложный способ умножения — настолько красивый графически, что я посвятил ему отдельную главу этой книги. В главе 26 — «Прекраснее листопада» — я раскрою вам тайны этого метода. Когда в позднем Средневековье он добрался до Европы, его называли умножением ревнивцев, потому что вертикальные линии в клеточках напоминали щели в ставнях, через которые ревнивцы подглядывали за своими супругами.

Хотя сейчас мы не представляем себе жизни без калькулятора, на самом деле калькулятор у людей имелся всегда. Это наши руки. Многие использовали для счета собственные пальцы. В Индии, Индокитае и Китае для счета использовалась каждая фаланга пальца. Большой палец состоит из двух фаланг, а остальные — из трех. Значит, на одной руке у нас имеется 14 фаланг. Получается, с помощью пальцев одной руки можно посчитать не только до пяти. Пользуясь двумя руками, китайцы могли досчитать до десяти миллионов!

Один из самых интересных способов умножать с помощью собственных пальцев — перемножать числа от 6 до 10. Этот способ проще некуда. Числу 6 соответствует один палец, числу 7 — два пальца, а числу 8 — три. Умножим 7 на 8. Для этого придется загнуть два пальца на одной руке и три — на другой. Всего получится пять загнутых пальцев. Каждый из этих пяти пальцев соответствует десяти. Итого 50. Теперь надо перемножить не загнутые пальцы на каждой руке. На одной руке их три, а на другой — два.

3 × 2 = 6

Это количество — единицы. При умножении 7 на 8 мы складываем получившиеся десятки с единицами: 50 плюс 6 равно 56.

Ну а теперь пора приступать к быстрому счету и восхищаться возможностями, которые дарит нам наша удивительная система счисления. В следующей главе вы увидите, как перемножать двузначные числа, близкие к сотне. Почувствуйте скорость!