Доказательства

ОТ ВОЛШЕБСТВА К ПОНИМАНИЮ

Если бы я не понимал принципа работы правил, я бы никогда не стал к ним прибегать. Однако математические доказательства могут показаться многим довольно-таки страшными, поэтому я решил собрать их все здесь, в самом конце книги.

ГЛАВА 5

Перемножая два числа меньше 100, мы можем проводить вычисления по следующей формуле:

(100 ‒ a)(100 ‒ b) = 1002 ‒ 100a ‒ 100b + ab = 100(100 ‒ a ‒ b) + ab.

ГЛАВА 6

Возводя в квадрат числа, заканчивающиеся на 5, мы можем использовать формулу для квадратичного тождества первого типа.

Вы, возможно, помните квадратичное тождество первого типа?

(a + b)2 = a2 + 2ab + b2

В этом случае b равно 5.

(10a + 5)2 = 100a2 + 100a + 25 = 100a(a + 1) + 25

Если вам хочется найти доказательство полегче, можно сначала взвести в квадрат число, в котором 5 стоит после запятой:

(a + ½)2 = a2 + a + ¼ = a(a + 1) + 0,25

В этой формуле полезно разобраться. Единственное, о чем надо помнить, — поставить запятую перед началом вычислений и убрать ее потом. Именно этому правилу и научила меня моя строгая учительница математики перед тем, как уйти на пенсию. Для несчастного школьника, которому не хватало фантазии придумать правило самому, эта формула стала настоящим откровением.

ГЛАВА 7

Возводя в квадрат числа, заканчивающиеся на 25, можно пользоваться квадратичным тождеством первого типа:

(a + b)2 = a2 + 2ab + b2

В этом случае b равно 25.

(100a + 25)2 = 10000a2 + 5000a + 625 = 1000a(10a + 5) + 625

По правде говоря, это доказательство довольно-таки неудобоваримое. Если вам нужно что-то попроще, для начала возведем в квадрат число, в котором 25 стоит после запятой. Решив пример, уберем запятую.

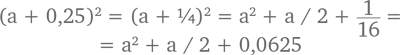
ГЛАВА 8

Доказательство чудесного метода быстрого счета вовсе не такое сложное, каким кажется на первый взгляд:

a = первый множитель,

b = второй множитель,

c = референтное число для первого множителя,

d = разница между референтным числом для второго множителя и референтным числом для первого множителя.

Образец:

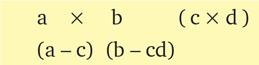
Доказательство:

(b + (a ‒ c)d) c + (a ‒ c)(b ‒ cd) =

= (b + ad – cd)c + (ab ‒ acd ‒ cb + c2d) =

= bc + acd ‒ c2d + ab ‒ acd ‒ cb + c2d = ab

ГЛАВА 9

Доказательство полностью основано на квадратичном тождестве первого типа.

Правило пятидесяти:

(50 + a)2 = 502 + 100a + a2 = 100(25 + a) + a2

Правило пятисот:

(500 + a)2 = 5002 + 1000a + a2 = 1000(250 + a) + a2

ГЛАВА 10

Это доказательство того, как перемножить два числа, в которых одинаковые десятки, а сумма единиц составит 10:

(10a + c)(10a + (10 ‒ c)) = 100a2 + 10a(10 ‒ c) + 10ca + + c(10 ‒ c) = 100a2 + 100a + c(10 ‒ c) = 100a(a + 1) + c(10 ‒ c)

ГЛАВА 11

Этот метод полностью опирается на квадратичное тождество третьего типа:

(a + b)(a ‒ b) = a2 ‒ b2

ГЛАВА 12

Этот метод тоже основывается на квадратичном тождестве третьего типа:

(a ‒ b)(a + b) = a2 ‒ b2

Если перенести b2 на другую сторону, получим решение:

a2 = (a ‒ b)(a + b) + b2