Книга: Честная ложь. Почему мы продолжаем верить в то, что портит нам жизнь
Назад: Формула пастора
Дальше: На плечах великанов
Байесовские дебри
Указатель пути в числовых дебрях – условно достоверно – просчитать мошенника – восприятие и предрассудки
Чтобы было легче сориентироваться, прямо на входе в числовые дебри пастора Байеса (Вход свободный!) на большом указателе яркой краской начертана формула:
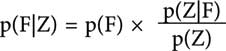
А рядом улыбающийся смайлик. Очень полезно, сразу смекаешь, что к чему.
Что же означают странные знаки в этой диковинной последовательности? Согласно условиям, 4 маленьких «р» – это различные вероятности, а буквы в скобках указывают, какие именно.
«F» – это предположение, что подброшенная монетка была настоящей. «Z» обозначает выпадение решки. Остаются еще странные вертикальные линии. Их следует понимать как «если», вводящее условие вероятности.
p(F|Z) – вероятность того, что играют неподдельной монетой, если она падает решкой вверх. Значение p(F|Z) – это, собственно, цель нашего эксперимента, на основе его мы и будем судить о том, какой была монета. Остаток формулы показывает, как вычислить интересующий нас показатель.
Вторая вероятность в формуле, p(Z|F), – так называемая обратная. То есть вероятность того, что решка выпадает, если монета не поддельная. Как мы уже знаем, она составляет 50 % или 0,5.
Всегда требуется немного усилий, когда дело касается реализации основной цели восприятия, а именно, улучшения нашей жизни. В долгосрочной перспективе те, кто избегает этих усилий, причинят вред себе и окружающим.
Теорема Байеса демонстрирует, что, несмотря на взаимозависимость, обе вероятности не идентичны. Томас Байес и его формула говорят, что мы можем вычислить искомую вероятность из тех, которые нам уже известны. Тогда в зависимости от того, как упадет монета, будет формироваться и наше к ней отношение.
В формуле недостает еще двух выражений – p(F) и p(Z). Это общая вероятность того, что монета настоящая и будет падать решкой вверх. Обе вероятности не имеют вертикальной линии и, значит, ничем не обусловлены. Поскольку в нашем примере у игрока 2 монетки, одна из которых настоящая, а другая поддельная, мы можем легко установить исходное значение p(F). При случайном выборе из двух монет оно составит 50 %: p(F) = 0,5.
p(Z) – вероятность того, что выпадет решка, тоже проста в вычислении. Монета может упасть либо орлом вверх, либо решкой, и если нам больше ничего не известно о ней, то оба варианта одинаково возможны. Таким образом, p(Z) = 0,5.
Теперь, согласно формуле Байеса, вероятность того, что монета не поддельная, если она падает решкой вверх, выражается так: p(F|Z) = 0,5 × 0,5 / 0,5. То есть вероятность остается неизменной. Но мы хотим знать не только, что настоящая монета приземляется решкой вверх, но, прежде всего, с какой из монет мы имеем дело. Применяя формулу Байеса, рассмотрим вероятность для оцинкованной монеты. Следуя той же логике, мы записываем формулу: p(G|Z) = p(G) × p(Z|G) / p(Z). Как и прежде, p(G) и p(Z) равны 0,5 каждая.
Но p(Z|G), то есть вероятность того, что выпадет решка, если подбрасываемая монетка оцинкована, теперь выше. В таком случае это происходит в 3 раза чаще. В среднем в трех из четырех случаев. Таким образом, p(Z) равно ¾ или 0,75. Результат вычисления таков: p(G|Z) = 0,5 × 0,75 / 0,5 = 0,75.
Итак, у нас есть p(G|Z) = 0,75 и p(F|Z) = 0,5. Это единственно существующие возможности в нашем случае, потому что монета либо оцинкована, либо нет. Обе вероятности должны, как и ранее, в сумме давать 1. Для этого мы делим каждое значение на их сумму 0,5 + 0,75 = 1,25.
Так, мы получаем: p(G|Z) = 0,75 / 1,25 = 0,6 и p(F|Z) = 0,5 / 1,25 = 0,4.
Вероятность того, что в нашем примере играла не оцинкованная монета, снизилась с 50 % до 40, при условии, что выпала решка. После броска p(F) = 0,4, а p(G) = 0,6.
Что же произойдет, если мы подкинем эту же монету во второй раз и снова выпадет решка? Всю предварительную работу мы уже проделали. Значения вероятностей остаются прежними, что и в первом раунде, только p(F) и p(G) изменились после первого броска.
Итак, мы имеем: p(F|Z) = 0,4 × 0,5 / 0,5 = 0,4 и p(G|Z) = 0,6 × 0,75 / 0,5 = 0,9. Оба результата делим на их сумму, которая теперь составляет 1,3, и получаем p(F|Z) = 4/13 и p(G) = 9/13, или приблизительно 31 % и 69 %.
Мы достаточно потренировались и теперь можем все повторить в третий раз. На этот раз у нас получается p(F|Z) = 4/13 и p(G|Z) = 27/26, а после сведения суммы до единицы (путем деления 35/26) уже p(F) = 8/35 и p(G) = 27/35, что примерно 23 % и 77 %.
Как предсказывалось ранее, с каждым броском, при котором выпадает решка, вероятность того, что мы имеем дело с оцинкованной монетой, возрастает с первоначальных 50 % до 77 после третьего броска. Иначе говоря, если трижды выпала решка, то вероятность того, что фокусник пытается нас надуть, в 3 раза выше, чем вероятность честной игры.
Так, получив несколько отдельных результатов, можно сформулировать суждение. Следует отметить, что наше мнение о ситуации, сформированное расчетами, никогда не может быть точно на 100 %, сколько бы раз ни выпадала решка. Значение p(F|Z) не может достигнуть нуля и исчезнуть из уравнения. Наше суждение всегда остается лишь оценкой вероятности и не лишено сомнения.
Внимания заслуживает и другой момент.
Свои расчеты мы начали с предположения, что игрок вытащит из кармана оцинкованную монетку или настоящую с одинаковой долей вероятности. Однако если нам известно, что человека уже обличали в мошенничестве, то мы подозреваем его в нечистой игре с самого начала. Скажем так: мы с самого начала ставим 1:3, что он вытащит поддельную монету. Тогда уже в начале игры p(F) = 0,25 и p(G) = 0,75.
Если теперь трижды выпадет решка, эта вероятность вырастет с 25/75 % до примерно 18/82 % после первого, 13/87 % после второго и 9/91 % после третьего броска. Вероятность обмана возросла в 10 раз. И это без изменения даже мельчайших деталей, лежащих в основе наблюдений.
На этом месте мы выходим из волшебных дебрей пастора Байеса. Итак, можно сделать потрясающий вывод, что в основе всего лежит точная формула Байеса и нюансы теории вероятностей. Но вибрации от этого потрясения волнами проходят через все, что мы воспринимаем и ощущаем.
Ведь не только p(F) и p(G) влияют на нашу оценку ситуации. Мы даже не можем начать весь расчет, пока не решим, какое значение должны иметь эти две вероятности. На основании чего мы должны это сделать, спросите вы. А нам нечего на это ответить, потому что на данный момент мы еще не сделали никаких наблюдений.
Значение начальных параметров мы задаем исходя из собственных предубеждений.
Назад: Формула пастора
Дальше: На плечах великанов

