График рассеивания – классический способ показать взаимосвязь. На оси X показана одна количественная переменная, на оси Y – другая. По направлению, его выраженности, по форме расположения точек можно судить о наличии/отсутствии и силе взаимосвязи, о характере корреляции между переменными.

Чаще всего людей интересует, есть ли связь между переменными, положительная она или отрицательная. Если связь положительная, при возрастании значений одной переменной возрастают и значения другой. Классический пример – положительная связь между расходами на маркетинг и объемом продаж.

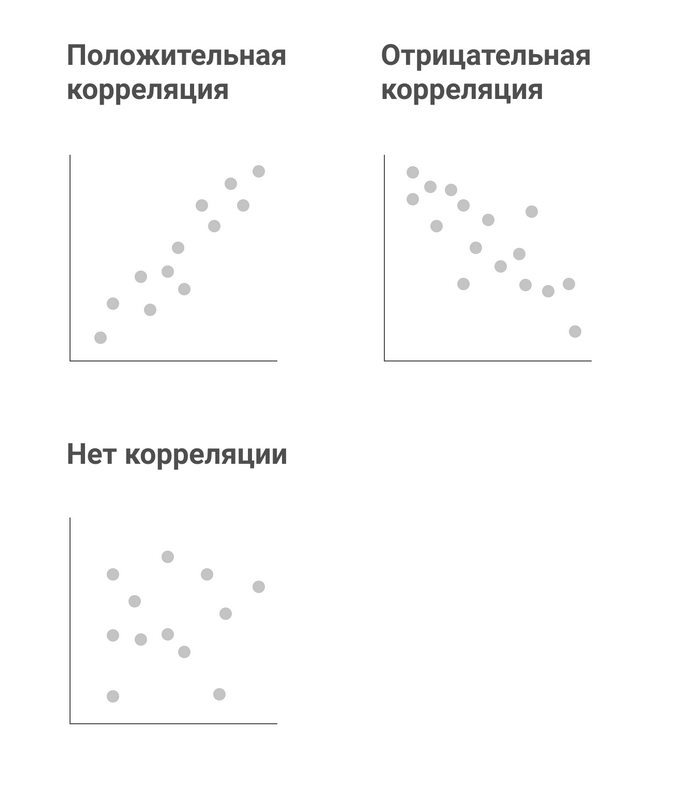
Есть мнение, что широкая аудитория гораздо хуже понимает графики рассеивания, чем столбиковые, круговые и линейные диаграммы. В одном из крупнейших мировых СМИ – Нью-Йорк Таймс – долгие годы существовал запрет на использование графиков рассеивания.

Я считаю, что в ряде случаев графики рассеивания все же могут быть эффективными и наглядными, в том числе и в презентациях. Безусловно, они предполагают личное объяснение.

Кроме того, существует прием, который может сделать графики рассеивания гораздо более наглядными. Это объединение точек в группы и разделение пространства системы координат на смысловые зоны. Выделение смысловых зон можно сделать по среднему или медианному значению по каждой из переменных (губернаторы на примере ниже). Или на основе других значений.

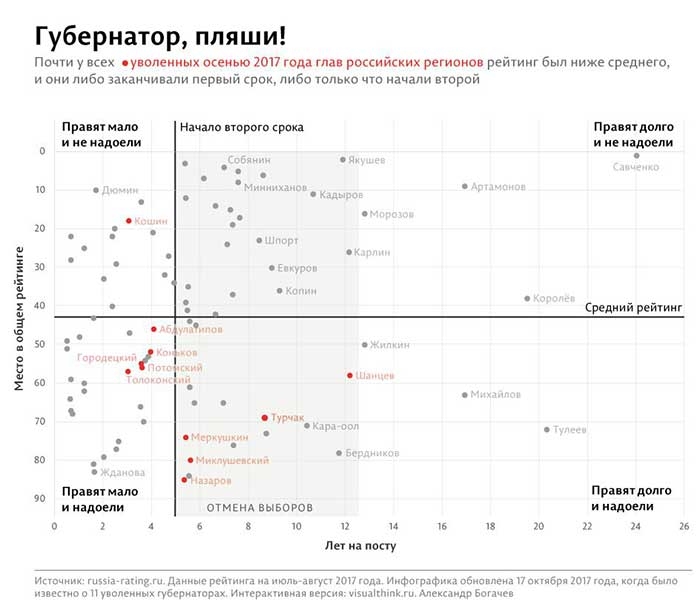
Работа автора

Выделение смысловых зон значительно облегает считывание информации на графике. Оно позволяет донести сообщение с помощью объединения значений в группы.

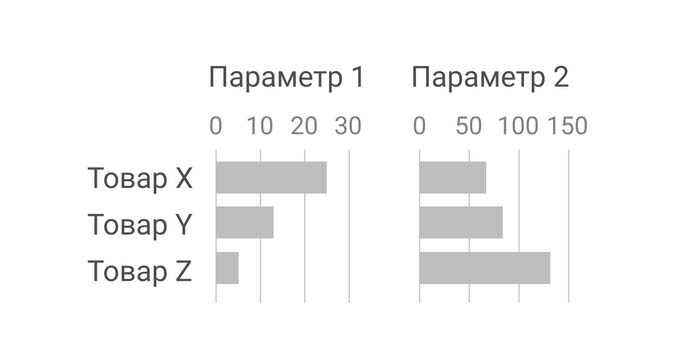
Одна из популярных альтернатив для показа взаимосвязи между двумя переменными – две линейчатые диаграммы, расположенные рядом. Они делают очевидной обратно пропорциональную связь: в одном ряду значения возрастают, а в другом, соответственно, убывают.

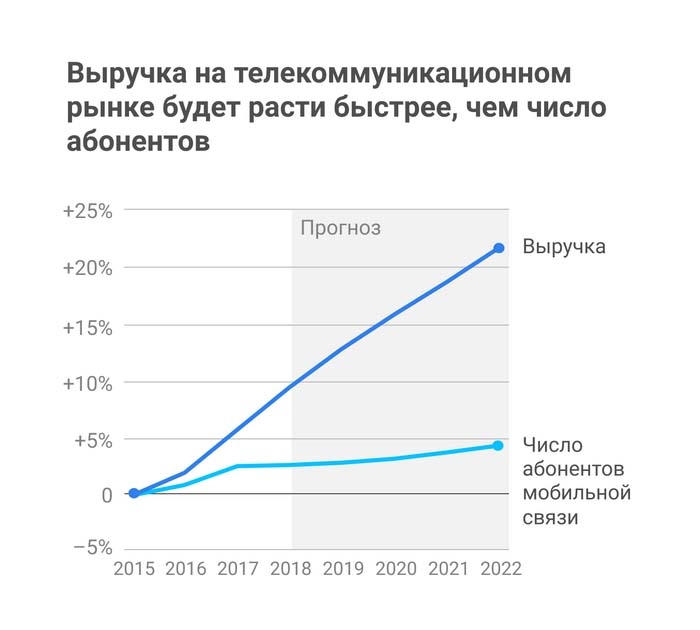
Часто для показа взаимосвязи используют комбинированные диаграммы, сочетающие столбиковую диаграмму и линейный график. Обычно, это не самое удачное решение, так как может создавать ложное ощущение корреляции.

Если вы все же решили использовать подобную комбинированную диаграмму, стоит соблюдать несколько правил:

• Не больше двух рядов данных на одном графике. Если нужно больше, лучше сделать несколько графиков

• Четкое указание на то, какая шкала к какому ряду данных относится

• Использование сопоставимых размерностей у шкал. Если в одной размерности определенное расстояние означает, что показатель изменился вдвое, то и в другой должно быть то же самое. Иначе можно легко ввести читателя в заблуждение относительно предполагаемой причинной связи между переменными

• Если это уместно, лучше использовать проценты от исходного уровня вместо абсолютных значений

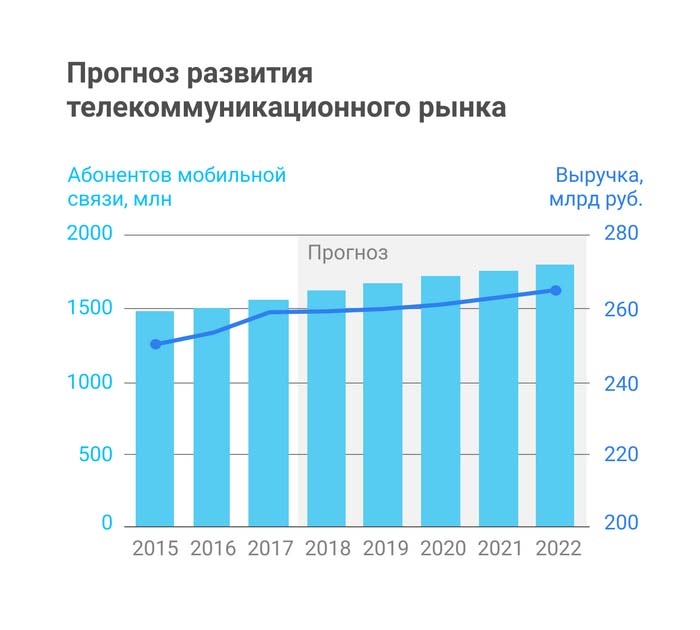
В этом варианте графика крайне сложно понять степень роста каждого показателя относительно друг друга. Чтобы сделать его очевидным, перестроим оба графика:

Для более глубокого понимания передаваемых сообщений с помощью пяти основных видов диаграмм рекомендую обратиться к классическому труду Джина Желязны «Говори на языке диаграмм».