4. Рецепт горячей Вселенной
Из наблюдений, о которых шла речь в предыдущих двух главах, стало ясно: Вселенная, во-первых, расширяется, а во-вторых, заполнена вездесущим излучением, имеющим сегодня температуру 3 К. Последнее, по-видимому, осталось с того времени, когда космос был непрозрачным и, кроме того, в 1000 раз меньше и горячее, чем сейчас. (Когда мы говорим, что Вселенная была в 1000 раз меньше, чем сейчас, то, как обычно, имеем в виду, что расстояния между парами типичных галактик были в 1000 раз короче.) Прежде чем начать рассказ о первых трех минутах, на последнем подготовительном занятии обратимся к еще более ранним временам – когда Вселенная была еще меньше и горячее. Только теперь для выяснения царивших тогда физических условий вместо оптических и радиотелескопов воспользуемся нашим умственным зрением.
Как было отмечено в конце главы 3, когда Вселенная имела размеры в 1000 раз меньшие, чем сейчас, и вот-вот должна была стать прозрачной для излучения, происходил также и переход от ее радиационно- к материально-доминированной стадии. Мало того, что на первой из них фотонов было много (на один нуклон приходилось столько же фотонов, сколько и ныне), так они еще и несли в себе бо́льшую энергию. В итоге энергия во Вселенной содержалась в основном в излучении, а не в массе. (Фотоны, напомним, – это безмассовые частицы, «кванты», из которых, согласно квантовой механике, состоит свет.) Следовательно, в грубом приближении можно считать, что в ту эпоху во Вселенной присутствовало исключительно излучение, а вещества не было совсем.
Здесь нужно сделать важное замечание. Ниже мы увидим, что век излучения начался через несколько минут после рождения Вселенной – когда температура упала до нескольких миллиардов кельвинов. А до этого момента вещество играло-таки свою роль. Но оно было совсем не тем, которым заполнена современная Вселенная. Однако прежде чем забираться так далеко в прошлое, давайте пробежимся по эпохе, в которой безраздельно властвовало излучение – от первых минут до нескольких сотен тысяч лет с начала космической истории, когда на первый план снова вышло вещество.
Чтобы проследить этот период жизни Вселенной, нам всего лишь нужно знать, насколько горячо было в космосе в тот или иной момент времени. Или, другими словами, как температура Вселенной связана с ее размером.
На этот вопрос особенно легко ответить в условиях беспрепятственного распространения излучения, что имеет место в настоящее время. Тогда длина волны каждого фотона растягивается (вследствие красного смещения) пропорционально размеру расширяющейся Вселенной. А средняя длина волны у чернотельного излучения, как было показано в предыдущей главе, обратно пропорциональна температуре. Следовательно, температура меняется обратно пропорционально размеру Вселенной.
К счастью для космолога-теоретика, это соотношение сохраняется и для случая, когда излучение нельзя рассматривать как свободное. В радиационно-доминированную эпоху из-за частых столкновений фотонов с относительно немногочисленными электронами и нуклонами Вселенная была непрозрачна. Но в перерыве между столкновениями фотон распространялся свободно. Значит, длина его волны тоже росла пропорционально размеру Вселенной. А поскольку на одну частицу вещества приходилось много фотонов, то это температура вещества зависела от температуры фотонов, а не наоборот. Таким образом, когда Вселенная была, например, в десять тысяч раз меньше, чем сейчас, ее температура была во столько же раз больше – т. е. около 30 тысяч градусов Кельвина. При такой жаре излучение заведомо преобладало.
Все больше углубляясь в прошлое, мы наконец обнаружим момент, когда энергия фотонов была настолько высока, что они, сталкиваясь между собой, могли превращать свою энергию в частицы вещества. Мы покажем, что в первые минуты жизни Вселенной такие частицы, рожденные из чистой лучистой энергии, выступали на равных с излучением. Они не только влияли на скорости ядерных реакций, но и определяли темп расширения самой Вселенной. Следовательно, установить ход событий в те давние времена можно, посчитав, насколько горяча должна была быть Вселенная, чтобы лучистая энергия начала превращаться в частицы вещества, и сколько этих частиц тогда появилось.
Понять, как из излучения рождаются частицы, проще всего в рамках квантовой теории света. Два кванта излучения – два фотона – столкнувшись, могут аннигилировать (исчезнуть), а вся их энергия и импульс перейдут к двум или более частицам вещества. (Этот процесс косвенно наблюдается на современных высокоэнергетичных ускорителях.) Однако специальная теория относительности Эйнштейна гласит: даже неподвижная частица вещества обладает определенной энергией покоя, которую можно вычислить по известной формуле E = тс 2. (Здесь с – это скорость света. Именно из массы черпается энергия в ядерных реакциях.) Следовательно, чтобы из двух сталкивающихся лоб в лоб фотонов получить две частицы массы т, энергия каждого из них должна составлять не менее тс 2. Если она окажется большей, то реакция все равно произойдет – разве что новорожденные частицы благодаря избытку энергии приобретут высокую скорость. Но если она будет меньшей, чем тс 2, то частицы массы т не появятся ни при каких условиях: энергии не хватит даже на то, чтобы образовать массу этих новых частиц.
Чтобы судить, насколько эффективно излучение производит частицы, очевидно, нужно знать характерную энергию его фотонов. Ее мы вычислим, применив простое эмпирическое правило: характерная энергия фотона равна произведению температуры излучения на фундаментальную постоянную статистической физики – постоянную Больцмана. (Людвиг Больцман наряду с американским ученым Виллардом Гиббсом считается основателем современной статистической физики. Говорят, одной из причин его самоубийства в 1906 г. послужило неприятие своих работ с философской точки зрения. Впрочем, имевшиеся тогда противоречия давно разрешены.) Численное значение постоянной Больцмана – 0,00008617 электронвольта на кельвин. Например, при температуре 3000 К, когда Вселенная постепенно прояснилась, характерная энергия фотонов равнялась (3000 К умножить на постоянную Больцмана) примерно 0,26 электронвольта. (Один электронвольт, напомним, – это энергия, которую приобретает один электрон, пройдя разность электрических потенциалов в один вольт. Скажем, энергия химических реакций – порядка одного электронвольта на атом. Именно поэтому излучение с температурой 3000 К не дает большинству электронов войти в состав атомов.)
Итак, чтобы в столкновении двух протонов получить частицы массы m, энергия каждого фотона должна равняться как минимум энергии покоя mc 2. А поскольку характерная энергия фотона – это температура, умноженная на постоянную Больцмана, получается, что температура излучения должна быть по крайней мере не меньше, чем энергия покоя mc 2, деленная на постоянную Больцмана. Иными словами, для каждого сорта частиц существует свой «температурный порог» – соответствующие частицы начинают рождаться из лучистой энергии только тогда, когда он достигнут.
Например, возьмем самые легкие известные частицы – электрон e– и позитрон e+. Позитрон – «античастица» электрона, т. е. у него те же масса и спин, но заряжен он противоположно (положительно, а не отрицательно). Когда электрон сталкивается с позитроном, их заряды компенсируются, а энергия, содержащаяся в массе частиц, переходит в чистое излучение. Кстати, это объясняет, почему позитроны так редки: едва родившись, позитрон наталкивается на один из присутствующих в изобилии электронов и аннигилирует. (Позитроны были обнаружены в космических лучах в 1932 г.) Процесс аннигиляции может идти и в обратном направлении: сталкиваясь, два фотона образуют электрон-позитронную пару, а их энергия переходит в массу электрона и позитрона.
Чтобы после лобового столкновения из двух фотонов получились электрон и позитрон, энергия каждого из фотонов должна превосходить энергию покоя mc 2 электрона с позитроном – т. е. 511 003 электронвольт. Поделив эту величину на постоянную Больцмана (0,00008617 электронвольта на кельвин), найдем температурный порог, при котором фотоны достаточно энергичны, – 6 миллиардов кельвинов (6 × 109 К). Если его превысить, фотоны начинают с легкостью производить электроны с позитронами, и последние появляются в больших количествах.
(К слову, температурный порог 6 × 109 К заметно выше характерных температур современной Вселенной. Даже в центре Солнца всего 15 миллионов градусов. Неудивительно, что фонтаны электронов и позитронов из лучей света сегодня не бьют.)
Все это относится к любому сорту частиц. Фундаментальный закон современной физики гласит: у каждой из них есть своя античастица – с точно такими же массой и спином, но противоположно заряженная. Единственное исключение делается для некоторых истинно нейтральных частиц – например, для фотона, который, можно считать, является своей собственной античастицей. Соотношение между электроном и позитроном – это соотношение взаимности: позитрон является античастицей электрона, а электрон – позитрона. В столкновении фотонов можно получить любую пару частица – античастица, нужно лишь, чтобы фотоны были достаточно энергичны.
(Античастицы – прямое математическое следствие законов квантовой механики и специальной теории относительности Эйнштейна. Существование антиэлектрона теоретически предсказал в 1930 г. Поль Адриен Морис Дирак. Не желая включать в свою теорию неизвестную частицу, он отождествил антиэлектрон с протоном – единственной известной тогда положительно заряженной частицей. Экспериментальную базу под теорию античастиц подвело открытие позитрона в 1932 г. Благодаря этому заодно стало ясно, что протон не является античастицей электрона: у него своя античастица – антипротон, открытый в 1950-х гг. в Беркли.)
Если выстраивать частицы по массе, то после электрона и позитрона идут мюон μ– (своего рода тяжелый нестабильный электрон) и его античастица μ+. Как и в случае с электроном и позитроном, μ– и μ+ имеют противоположные заряды, но равные массы. И они тоже могут родиться при столкновении двух фотонов. Энергия покоя тс 2 каждой из частиц μ– и μ+ составляет 105,6596 миллиона электронвольт. Деля ее на постоянную Больцмана, получаем температурный порог в 1,2 тысячи миллиардов градусов (1,2 × 1012 К). Температурные пороги для других частиц приведены в таблице I на с. 212. Глядя на эту таблицу, нетрудно перечислить все частицы, которыми в тот или иной момент космической истории была наполнена Вселенная: достаточно отмести все, температурный порог которых выше температуры космоса в то время.
Но пусть температура Вселенной выше порогового значения для некоего вида частиц. Сколько именно тогда их будет? При столь высоких температуре и плотности, которые царили в ранней Вселенной, количество частиц определяется условиями теплового равновесия. Оно должно быть таким, чтобы каждую секунду появлялось ровно столько частиц, сколько исчезает. (Предложение равно спросу.) Частота, с которой пары частица – античастица будут аннигилировать, превращаясь в фотоны, приблизительно равна частоте, с которой из пар фотонов с подходящей энергией будут рождаться частицы и античастицы. Таким образом, из условия теплового равновесия следует: число частиц каждого сорта, для которого превышен температурный порог, примерно равно числу фотонов. Если первых меньше, чем последних, они будут появляться интенсивнее, чем аннигилировать, и начнут прибывать. А если наоборот – станут быстро исчезать и их количество снизится. Например, при температуре выше 6 миллиардов кельвинов число электронов и позитронов, вместе взятых, должно было равняться количеству фотонов. Другими словами, тогда Вселенная была заполнена не только фотонами, а смесью из фотонов, электронов и позитронов.
Впрочем, при температурах выше пороговой частицы вещества напоминают фотоны. Средняя энергия частицы приблизительно равна ее температуре, умноженной на постоянную Больцмана. Поэтому, когда температура заведомо превышает пороговую, средняя энергия оказывается много больше энергии, запасенной в массе, и массой можно пренебречь. В таких условиях давление и плотность энергии частиц данного сорта пропорциональны четвертой степени температуры – так же, как у фотонов. Таким образом, можно считать, что в каждый момент времени Вселенную заполняют различные виды «излучения». Их столько, сколько имеется сортов частиц с превышенным температурным порогом. В частности, в любой момент времени плотность энергии в космосе пропорциональна четвертой степени температуры и числу сортов частиц, оказавшихся над температурным порогом. В современной Вселенной температуры настолько высокие, чтобы пары частица – античастица выступали наравне с фотонами, не встречаются (разве что в ядрах взрывающихся звезд). Тем не менее мы вполне уверены в нашем знании статистической физики, чтобы без опаски строить теории о том, к чему привели экстремальные условия в ранней Вселенной.
Если вдаваться в детали, следует помнить, что античастицы вроде позитрона (e+) считаются отдельным сортом частиц. Кроме того, некоторые частицы, – скажем, фотон и электрон – имеют по два состояния с разным спином, которые тоже учитываются как разные сорта. Наконец, есть частицы, к которым относится и электрон (но не фотон), подчиняющиеся особому закону – «принципу запрета Паули». Последний запрещает двум частицам занимать одно и то же состояние. Де-факто это приводит к тому, что вклад таких частиц в полную плотность энергии уменьшается в 8/7 раз. (Именно принцип Паули не дает всем электронам в атоме упасть на нижнюю оболочку и отвечает за сложную структуру атомных оболочек, нашедшую отражение в таблице Менделеева.) Эффективное количество сортов для каждой разновидности частиц можно найти в той же таблице I на с. 212, где приведены пороговые температуры. Плотность энергии во Вселенной при заданной температуре пропорциональна четвертой степени температуры и эффективному числу сортов частиц, чьи пороговые температуры ниже температуры Вселенной в данный момент.
А теперь зададимся вопросом: когда Вселенная была нагрета до таких запредельных температур? Темп расширения определяется балансом между гравитационным полем и радиальным импульсом заполняющего космос вещества. На ранних стадиях источником гравитационного поля во Вселенной служила суммарная плотность энергии фотонов, электронов, позитронов и т. д. Как мы видели, последняя зависит главным образом от температуры, которая, таким образом, может служить своего рода часами, отсчитывающими различные стадии расширения. Если вдаваться в подробности, то время, за которое плотность энергии падает от одного значения до другого, пропорционально разнице величин, обратных квадратным корням из этих плотностей (см. математическую заметку 3 на с. 237). Но нам уже известно, что плотность энергии пропорциональна четвертой степени температуры и числу сортов частиц, для которых температура Вселенной выше пороговой. Следовательно, до тех пор, пока температура не пересекает ни один из порогов, промежуток времени, за который Вселенная охлаждается от одной температуры до другой, пропорционален разнице обратных квадратов этих температур. Скажем, если сначала температура была 100 миллионов градусов (это заведомо ниже температурного порога электронов), а через 0,06 года (22 дня) упала до 10 миллионов градусов Кельвина, то можно предсказать, что через шесть лет она будет равна одному миллиону, через шестьсот – 100 тысячам и т. д. Охлаждение от 100 миллионов до 3000 градусов Кельвина (когда Вселенная становится прозрачной для излучения) заняло ни много ни мало 700 тысяч лет (рис. 8). Когда я говорю «лет», то, конечно, имею в виду некоторое количество абсолютных единиц времени – скажем, определенное число периодов обращения электрона вокруг ядра в атоме водорода. Ведь события, о которых мы говорим, происходили задолго до того, как Земля начала свой путь вокруг Солнца.
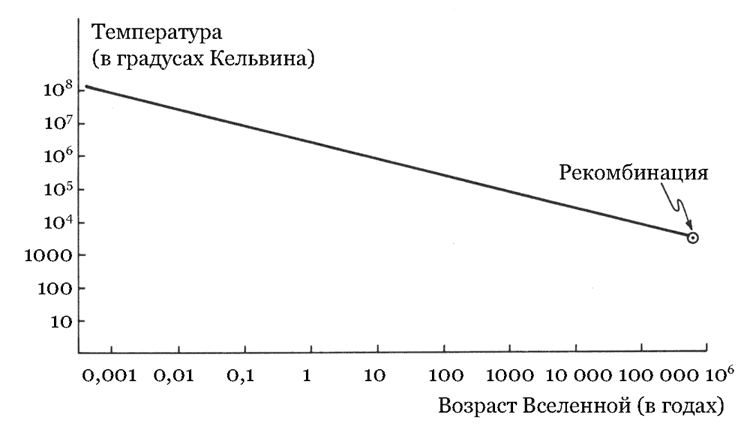
Рис. 8. Радиационно-доминированная стадия. Здесь изображена зависимость температуры Вселенной от времени: от конца эпохи нуклеосинтеза до рекомбинации ядер и электронов в атомы
Если бы во Вселенной в первые минуты ее жизни было точно поровну частиц и античастиц, они бы все до единой аннигилировали, едва температура опустилась ниже миллиарда градусов, – не осталось бы ничего, кроме излучения. Но против такого сценария есть убедительный аргумент – мы сами! Чтобы было из чего строить современную Вселенную, электронов должно было быть чуть больше, чем позитронов, протонов – чуть больше, чем антипротонов, а нейтронов – чуть больше, чем антинейтронов. В этой главе я до сих пор сознательно умалчивал об этих сравнительно скудных остатках вещества. Ими можно с хорошей точностью пренебречь, когда мы вычисляем темп расширения ранней Вселенной. Как показано в предыдущей главе, по плотности энергии нуклоны уступали излучению вплоть до температуры 4000 К. Однако эта малая толика электронов и нуклонов заслуживает самого пристального внимания – хотя бы потому, что эти частицы являются основным строительным блоком современной Вселенной.
Если все-таки принять, что в первые минуты существовал небольшой перевес вещества над антивеществом, возникает задача составить подробный реестр всех ингредиентов раннего мироздания. Список так называемых элементарных частиц, который каждые полгода публикует Лаборатория им. Лоуренса в Беркли, содержит в прямом смысле сотни наименований. Неужели нам придется перечислять, в каких количествах присутствует каждый из них? А может, элементарными частицами дело не ограничивается и нужно еще указать, сколько было разных атомов, молекул, соли, перца? В таком случае, решив, что Вселенная слишком непредсказуема и сложна для понимания, мы были бы на волоске от того, чтобы отказаться от попыток ее познать.
К счастью, она не настолько сложна. Чтобы узнать, каков ее рецепт, нужно лишь поглубже вдуматься в условие теплового равновесия. Я уже указывал, какое большое значение имеет тот факт, что Вселенная когда-то пребывала в нем. Именно благодаря ему мы с такой уверенностью говорим, чем был заполнен космос в прошлом. И все выводы этой главы строились на известных свойствах вещества и излучения в термодинамическом равновесии.
Когда физическая система приходит в тепловое равновесие (благодаря столкновениям или каким-либо другим процессам), некоторые величины в ней перестают меняться. Одна из них – полная энергия. Хотя, сталкиваясь, частицы обмениваются энергией, их общая энергия остается той же. Каждому закону сохранения соответствует своя величина, которую необходимо задать, прежде чем браться описывать свойства системы в тепловом равновесии. Если эта величина в равновесной системе сохраняется, то, естественно, из условия теплового равновесия ее значение получить нельзя – его необходимо задать заранее. Замечательное свойство равновесной системы состоит в том, что стоит задать сохраняющиеся величины, как все ее свойства вычисляются совершенно однозначно. Вселенная, как известно, прошла через стадию теплового равновесия. Значит, чтобы перечислить все ее ингредиенты на ранних стадиях, достаточно знать, какие физические величины в ходе расширения сохранялись и каковы были значения этих величин.
Обычно вместо полной энергии равновесной системы указывают ее температуру. В той системе, которая нас интересовала в первую очередь (излучение вкупе с равным количеством частиц и античастиц), больше ничего не нужно знать. Все ее свойства определяются температурой. Но в общем случае, помимо энергии, есть другие сохраняющиеся величины, значения которых необходимо задать.
Взять хотя бы стакан воды при комнатной температуре. В нем непрерывно идут химические реакции: молекулы воды распадаются на ион водорода (голый протон – ядро водорода, у которого отняли электрон) и гидроксильную группу (пару из атома кислорода и водорода, несущую один лишний электрон), и наоборот, из водородного иона и гидроксильной группы получаются молекулы воды. Причем исчезновение молекулы воды всегда сопровождается появлением иона водорода (и наоборот), а ионы водорода и гидроксильные группы всегда исчезают и появляются парами. Таким образом, сохраняющиеся величины в этой системе – это полное число молекул воды плюс число водородных ионов, а также число водородных ионов минус число гидроксильных групп. (Конечно, есть и другие сохраняющиеся величины – как, скажем, полное число молекул воды плюс число гидроксильных групп, – но все они выражаются через эти две фундаментальные величины.) Свойства воды в стакане будут полностью заданы, если мы скажем, что температура равна 300 К (комнатная температура в кельвинах), концентрация молекул воды и ионов водорода, вместе взятых, составляет 3,3 × 1022 штук на кубический сантиметр (примерно как у воды при давлении на уровне моря), а разность концентраций водородных ионов и гидроксильных групп равна нулю (это соответствует нулевому полному заряду). Пусть так получилось, что на 500 миллионов молекул воды приходится один ион водорода. Подчеркнем, что, составляя рецепт стакана воды, мы не должны задавать это число – его мы определим из условия теплового равновесия. С другой стороны, из последнего мы никак не узнаем, чему равны сохраняющиеся величины. Повысив или понизив давление, можно лишь, например, сделать концентрацию молекул воды и водородных ионов чуть меньше или чуть больше 3,3 × 1022. То есть для ответа на вопрос, что налито в наш стакан, необходимо это число задать.
Из этого примера также видно, что сохраняющиеся величины в разных условиях могут быть разными. Скажем, если наша вода попала внутрь звезды и имеет температуру в миллионы градусов, то молекулы и ионы легко диссоциируют, а атомы теряют свои электроны. В этом случае количество электронов, ядер кислорода и водородных ядер будет сохраняться. Концентрацию молекул воды и ионов водорода в таких условиях нужно не задавать, а, следуя законам статистической физики, вычислять. Впрочем, она будет невелика. (В аду в снежки не поиграешь.) На самом деле при этих условиях идут ядерные реакции, при которых меняется даже число ядер каждого сорта. Но меняется медленно, поэтому можно считать, что звезда постепенно переходит от одного равновесного состояния к другому.
Наконец, при температуре в несколько миллиардов градусов, до которой была нагрета ранняя Вселенная, на протоны и нейтроны распадаются даже атомные ядра. Реакции идут настолько бурно, что из лучистой энергии то и дело появляются пары частица – античастица – и тут же снова аннигилируют в излучение. В этих условиях количество каких бы то ни было частиц уже не является сохраняющейся величиной. В силе остается лишь небольшая горстка законов сохранения, которые не нарушаются (насколько нам известно) ни при каких условиях. Им соответствуют всего лишь три сохраняющиеся величины, значение которых следует заранее оговорить в нашем рецепте ранней Вселенной.
1. Электрический заряд. Мы можем создавать или избавляться от пар частиц с одинаковым по модулю, но противоположным по знаку зарядом, однако полный электрический заряд всегда остается постоянным. (В этом законе сохранения мы уверены больше, чем в других. Без него общепринятая теория электромагнетизма Максвелла теряет смысл.)
2. Барионное число. Барионы – собирательное наименование нуклонов (протонов и нейтронов) и более тяжелых нестабильных частиц, называемых гиперонами. Барионы и антибарионы появляются и исчезают парами. Один может перейти в другой, как это происходит при так называемом бета-распаде радиоактивных ядер, когда нейтрон превращается в протон. Однако число барионов за вычетом антибарионов (антипротонов, антинейтронов, антигиперонов) всегда остается постоянным. Протону, нейтрону и гиперонам можно присвоить «барионное число» +1, а соответствующим античастицам –1. Тогда полное барионное число будет сохраняться. В отличие от электрического заряда, оно, по-видимому, не входит ни в какие уравнения движения и, насколько нам известно, не создает полей наподобие электрического или магнитного. Барионное число – это своего рода отчетный показатель: его значение целиком в том, что он сохраняется.
3. Лептонное число. К лептонам относятся электрон и мюон (легкие отрицательно заряженные частицы), нейтрино (нейтральная частица с нулевой массой), а также их античастицы: позитрон, антимюон и антинейтрино. Несмотря на свои нулевые массу и заряд, нейтрино не менее реальны, чем фотоны: они обладают энергией и импульсом точно так же, как любая другая частица. Лептонное число – это еще один отчетный показатель: количество лептонов за вычетом антилептонов не меняется. (В 1962 г. в экспериментах с пучками нейтрино было обнаружено, что имеется как минимум два типа нейтрино: электронное и мюонное. Им соответствуют два типа лептонных чисел. Электронное лептонное число – это количество электронов и электронных нейтрино за вычетом их античастиц, а мюонное лептонное число – количество мюонов и мюонных нейтрино тоже за вычетом соответствующих античастиц. И та и другая величина, похоже, идеально сохраняются, но полной уверенности в этом пока нет.)
Хорошей иллюстрацией этих законов сохранения служит радиоактивный распад нейтрона n на протон p, электрон е– и антинейтрино (электронное). Для каждой из частиц заряд, барионное и лептонное числа указаны в таблице:
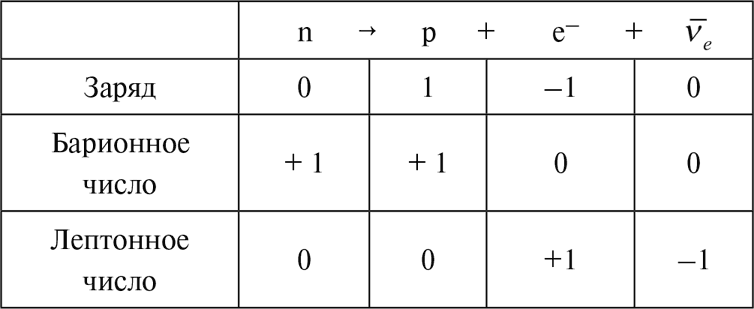
Читателю предоставляется возможность проверить, что для любой из сохраняющихся величин сумма ее значений для продуктов реакции равна ее значению для исходного нейтрона. Это и означает сохранение величины. Законы сохранения дают нам ценную информацию, показывая, какие реакции заведомо не происходят. Например, они запрещают нейтрону распадаться на протон, электрон и более чем одно антинейтрино.
Чтобы составить рецепт Вселенной на тот или иной момент времени, нужно задать заряд, барионное и лептонное числа на единицу объема, а также температуру. Законы сохранения гласят, что в любом объеме, который расширяется вместе со Вселенной, эти сохраняющиеся величины остаются постоянными. Следовательно, заряд, барионное и лептонное числа на единицу объема меняются обратно пропорционально размеру Вселенной. Но ведь и количество фотонов в единице объема обратно пропорционально кубу размера Вселенной. (В главе 3 мы говорили, что количество фотонов в единице объема пропорционально кубу температуры, а последняя, как было отмечено в начале этой главы, падает обратно пропорционально размеру Вселенной.) Таким образом, заряд, барионное и лептонное числа в расчете на один фотон тоже не меняются. А значит, наш рецепт, в котором заданы отношения этих сохраняющихся величин к количеству фотонов, верен во все времена. (Строго говоря, обратно пропорционально кубу размера Вселенной меняется не количество фотонов в единице объема, а энтропия единицы объема. Энтропия – фундаментальная величина статистической физики, характеризующая степень беспорядка в физической системе. Если опустить известный численный множитель, энтропия с большой точностью равна полному количеству частиц, находящихся в тепловом равновесии (сюда относятся как частицы вещества, так и фотоны). При этом у каждого сорта частиц есть свой вес, приведенный в таблице I на с. 212. Постоянные, которыми нам следовало бы описывать Вселенную, – это отношения заряда к энропии, барионного числа к энтропии и лептонного числа к энтропии. Между тем даже при очень высоких температурах количество частиц вещества имеет тот же порядок, что и число фотонов. Поэтому мы не очень ошибемся, если за эталон вместо энтропии примем количество фотонов.)
Заряд в расчете на один фотон оценить легко. Насколько нам известно, в среднем по Вселенной плотность электрического заряда равна нулю. Если бы у Земли и Солнца относительный избыток положительного заряда над отрицательным составлял одну миллионную одной миллионной одной миллионной одной миллионной одной миллионной одной миллионной (10–36), электрическое отталкивание между ними превысило бы силу тяготения. Если Вселенная конечна и замкнута, это утверждение можно возвести в ранг теоремы. Полный заряд такой Вселенной обязан равняться нулю, иначе силовые линии электрического поля беспрепятственно наматывались бы вокруг Вселенной, приводя к бесконечному электрическому полю. Но, независимо от того, замкнута она или открыта, электрический заряд в расчете на один фотон, не боясь впасть в заблуждение, можно считать равным нулю.
Оценить число барионов на фотон тоже нетрудно. Единственные стабильные барионы – это нуклоны (протон и нейтрон), а также их античастицы антипротон и антинейтрон. (По правде говоря, нейтрон в свободном виде нестабилен и распадается в среднем за 15,3 минуты. Однако благодаря ядерным силам в атомном ядре он приобретает устойчивость.) К тому же во Вселенной, насколько нам известно, антивещество если и встречается, то исключительно редко. (Подробности – ниже.) Следовательно, барионное число в любой области Вселенной с большой точностью равно количеству нуклонов. Из предыдущей главы мы узнали, что на один нуклон приходится миллиард фотонов реликтового излучения (это приблизительная цифра), поэтому число барионов на один фотон составляет одну миллиардную долю (10–9).
Это потрясающий вывод. Чтобы осознать его значение, обратимся к моменту в прошлом, когда температура превышала температурный порог протонов и нейтронов – десять миллионов миллионов градусов Кельвина (1013 К). Тогда Вселенная изобиловала нуклонами и их античастицами – их было почти столько же, сколько фотонов. Но барионное число – это разница между количеством нуклонов и их античастиц. Если она действительно была в миллиард раз меньше, чем число фотонов (а значит, примерно во столько же раз меньше полного количества нуклонов), то относительный избыток нуклонов над их античастицами составлял всего одну миллиардную. Получается, когда температура Вселенной упала ниже температурного порога нуклонов, все античастицы нашли себе пару и аннигилировали – остался лишь тот самый избыток частиц над античастицами, из которого в итоге и появился знакомый нам мир.
Некоторые теоретики отказывались верить, что в космологии может встретиться такое маленькое число, как одна миллиардная. Поэтому они выдвинули гипотезу: мол, на самом деле оно равно нулю – т. е. Вселенная содержит вещество и антивещество в равных количествах. Тогда для объяснения, почему нам кажется, будто на один барион приходится миллиард фотонов, приходится предположить, что незадолго до пересечения температурного порога для нуклонов космос был поделен на области с разными барионными числами. В одних имелся небольшой (в несколько миллиардных долей) избыток вещества над антивеществом, а в других – недостаток. Когда Вселенная достаточно охладилась и все частицы, нашедшие свою антиполовинку, аннигилировали, космос оказался разбит на области, в которых имелись либо только вещество, либо только антивещество. Сложность этого сценария в том, что никто и никогда не наблюдал во Вселенной антивещество. Космические лучи, вторгающиеся в верхние слои земной атмосферы, приходят, как считается, с окраин нашей Галактики и, возможно, частично из-за пределов Млечного Пути. Львиная их доля представляет собой вещество, а не антивещество. Фактически антипротон или антиядро в космических лучах не попадались еще никому. Кроме того, в наблюдениях не видно фотонов, которые должны были бы приходить из мест, где аннигиляция вещества и антивещества идет в космических масштабах.
Есть еще одна причина, по которой плотность фотонов (или, точнее, энтропии) может не подчиняться обратной кубической зависимости от размера Вселенной. В прошлом последняя могла отклоняться от теплового равновесия. Скажем, из-за какого-то трения или вязкости она нагрелась и появились «лишние» фотоны. Другими словами, сначала барионное число в расчете на фотон имело более или менее разумное значение (скажем, единицу), но с появлением новых фотонов упало до сегодняшней одной миллиардной. Проблема в том, что никому до сих пор не удалось придумать, как эти лишние фотоны могли бы родиться. Несколько лет назад я тоже над этим работал, но безуспешно.
В дальнейшем я больше не стану возвращаться к этим альтернативным теориям и буду предполагать, что барионное число на один фотон равно наблюдаемому значению, т. е. одной миллиардной.
А что же с плотностью лептонного числа Вселенной? Раз у нее нулевой электрический заряд, то на каждый электрон приходится ровно один протон. Протоны составляют около 87 % всех нуклонов современной Вселенной, поэтому количество электронов почти совпадает с полным числом нуклонов. Если бы электроны были сейчас единственными лептонами, мы бы немедленно заявили, что число последних (на один фотон) практически совпадает с числом барионов.
Однако помимо электрона и позитрона есть еще один сорт стабильных частиц, обладающих ненулевым лептонным числом. Нейтрино и антинейтрино, подобно фотону, не имеют электрического заряда и массы, но их лептонные числа равны соответственно +1 и –1. Таким образом, чтобы узнать лептонную плотность современной Вселенной, нужно сначала понять, сколько в космосе нейтрино и антинейтрино.
К сожалению, раздобыть эту информацию безумно сложно. Нейтрино, как и электрон, не подвержено влиянию ядерных сил, удерживающих протоны и нейтроны в ядре. (Иногда под словом «нейтрино» я буду также иметь в виду и антинейтрино.) Но, в отличие от электрона, оно не заряжено и, значит, нечувствительно к электрическим и магнитным полям, благодаря которым электрон притягивается к атомному ядру. Нейтрино вообще малочувствительны к каким бы то ни было силам. Хотя они, конечно, как и все во Вселенной, подвержены влиянию силы тяжести. Кроме того, нейтрино участвуют в слабых взаимодействиях, ответственных за некоторые радиоактивные процессы – например, за распад нейтрона (см. с. 132). Но обычное вещество в эти взаимодействия почти не вовлекается. Для демонстрации того, насколько трудно уловить нейтрино, обычно приводят следующий пример. Чтобы остановить или заставить рассеяться испущенное в некотором радиоактивном процессе нейтрино, на его пути необходимо поставить свинцовую стену толщиной в несколько световых лет. В ядерных реакциях, идущих в солнечном ядре, протоны непрерывно перерабатываются в нейтроны с испусканием нейтрино. Поэтому от Солнца к нам идет интенсивный поток последних. Днем нейтрино светят на нас сверху, а ночью, когда Солнце заходит за Землю, – снизу, так как наша планета для них полностью прозрачна. В науку нейтрино были введены Вольфгангом Паули, который предложил списать на их счет недостаток энергии, наблюдавшийся при распаде нейтрона. Зарегистрировать нейтрино напрямую удалось лишь в конце 1950-х гг. благодаря ядерным реакторам и ускорителям частиц, в которых нейтрино рождались в таких количествах, что сотня-другая застревала-таки в детекторе.
Но если нейтрино настолько слабо взаимодействуют с веществом, то они могут в изобилии заполнять Вселенную, а мы даже догадываться об этом не будем. Впрочем, кое-какие верхние ограничения на количество нейтрино и антинейтрино – далеко не самые строгие – наложить все же можно. Если бы этих частиц было слишком много, определенные распады в ядрах шли бы несколько не так, как должны. Да и темп расширения Вселенной замедлялся бы быстрее, чем это происходит. Тем не менее, несмотря на эти ограничения, нельзя исключить возможность того, что нейтрино и(или) антинейтрино присутствуют в космосе в таких же количествах и с такими же энергиями, как у фотонов.
Имея в виду эти оговорки, космологи, однако, обычно предполагают, что лептонное число (количество электронов, мюонов и нейтрино за вычетом соответствующих античастиц) в расчете на фотон весьма невелико – во всяком случае, много меньше единицы. Такое заключение делается из соображений аналогии: если число барионов на фотон мало, то почему должно быть велико количество лептонов? Это одна из самых шатких гипотез стандартной модели. К счастью, даже если она неверна, на общую картину, которую мы здесь рисуем, она почти не повлияет.
Конечно, при температуре выше температурного порога для электронов лептонов и антилептонов было много – по своему количеству электроны и позитроны могли сравниться с фотонами. Кроме того, Вселенная была настолько горячей и плотной, что в таких условиях в тепловом равновесии находились даже юркие нейтрино – и их число тоже было сравнимо с количеством фотонов. Предпосылка, заложенная в стандартную модель, состоит в том, что разница в числе лептонов и антилептонов была и есть значительно меньше количества фотонов. Не исключено, что существовал небольшой избыток лептонов над антилептонами (как это имеет место в случае с барионами и антибарионами), который сохранился до сегодняшнего дня. Нейтрино и антинейтрино к тому же взаимодействуют так слабо, что многие из них, возможно, до сих пор не нашли себе партнера, чтобы аннигилировать. В этом случае в современной Вселенной их было бы примерно поровну и их количество было бы сравнимо с числом фотонов. В следующей главе мы увидим, что такой сценарий сегодня довольно популярен в космологии. Но не стоит и надеяться, что в обозримом будущем нам удастся зарегистрировать обширный океан нейтрино и антинейтрино.
Итак, вот наш рецепт ранней Вселенной. Возьмите заряд в расчете на фотон равным нулю, на каждый миллиард фотонов добавьте по одному бариону, а лептонное число примите равным некоторой малой величине. Задайте температуру в нужный вам момент времени как отношение современного размера Вселенной к размеру в интересующую вас эпоху, умноженное на 3 К (современная температура реликтового излучения). Хорошенько перемешайте, чтобы микроскопические распределения частиц различных сортов отвечали требованию теплового равновесия. Поместите все это во Вселенную, темп расширения которой определяется силой тяготения этого самого вещества. Если запастись терпением, то через некоторое время из этой мешанины должен получиться наш сегодняшний мир.

