Заметка 4. Излучение абсолютно черного тела
Согласно планковскому распределению энергия du чернотельного излучения в единице объема и в узком интервале длин волн от λ до λ + dλ равна:
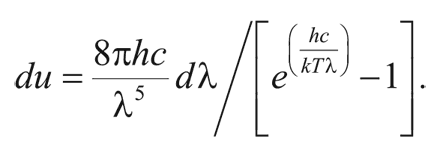
Здесь T – температура, k – постоянная Больцмана (1,38 × 10¯16 эрг/K), c – скорость света (299 729 км/с), e – число, равное 2,718…, и h – постоянная Планка (6,625 × 10¯27 эрг с), которую в эту формулу ввел Макс Планк.
В случае длинных волн для знаменателя в формуле Планка верно приближенное равенство:
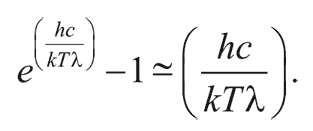
Таким образом, в данном диапазоне длин волн планковское распределение сводится к виду:
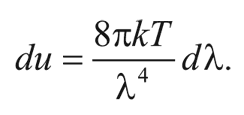
Эта формула выражает закон Рэлея – Джинса. Если бы он соблюдался для сколь угодно коротких волн, производная du/dλ стремилась бы к бесконечности при λ→0 и полная плотность энергии чернотельного излучения была бы бесконечной.
К счастью, планковское распределение достигает максимума при длине волны:
λ = 2014052 hc/kT,
а затем на коротких волнах следует крутой спад. Полная плотность энергии излучения абсолютно черного тела выражается через интеграл:
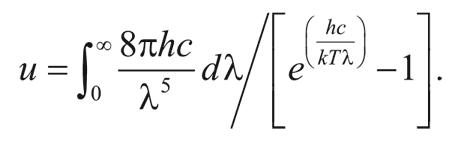
Интегралы такого вида легко найти в стандартных таблицах определенных интегралов. После интегрирования получаем:
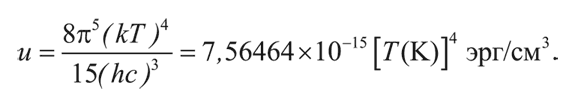
Эта формула выражает закон Стефана – Больцмана.
Распределение Планка легко переписать в терминах квантов света – фотонов. Энергия фотона вычисляется по формуле
E = hc / λ.
Следовательно, число фотонов чернотельного излучения dN в единице объема и в узком интервале длин волн от λ до λ + dλ равно:
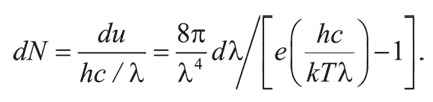
Тогда полное число фотонов в единице объема:
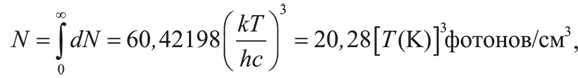
а средняя энергия фотона:
Еср. = и / N = 3,73 ×10¯16 [T (K)] эрг.
Теперь рассмотрим, что происходит с чернотельным излучением в расширяющейся Вселенной. Допустим, размер последней увеличился в f раз. Например, если Вселенная расширилась в два раза, то f = 2. Как мы знаем из главы 2, все длины волн пропорционально возрастут до значения:
λ' = f λ.
В конечном состоянии плотность энергии du' в новом интервале длин волн от λ' до λ' + dλ' меньше по сравнению с первоначальной плотностью энергии du в старом диапазоне длин волн от λ до λ + dλ по двум причинам:
1. Поскольку объем Вселенной вырос в f 3 раз, а фотоны никуда не исчезают и ниоткуда не появляются, то их число в единице объема упало в 1/f 3 раз.
2. Энергия одного фотона обратно пропорциональна длине волны, и, значит, она уменьшилась в 1/f раз. Следовательно, полная плотность энергии уменьшилась в 1/f 4 раз (1/f 3 умножить на 1/f):
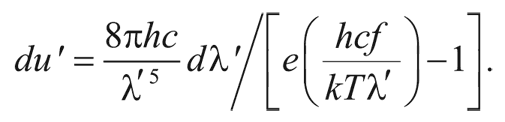
Переписывая эту формулу через новую длину волны λ', получим:
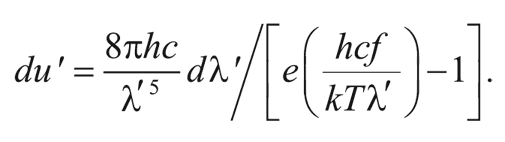
Но это опять та же самая формула для du в зависимости от λ и dλ, только вместо температуры Τ стоит новая температура:
Τ' = Τ / f.
Таким образом, приходим к заключению: свободно расширяющееся чернотельное излучение в любой момент времени описывается формулой Планка с температурой, обратно пропорциональной коэффициенту расширения.
Заметка 5. Масса Джинса
Чтобы из сгустка вещества образовалась гравитационно связанная система, его гравитационная потенциальная энергия должна превосходить энергию теплового движения. Гравитационная потенциальная энергия сгустка радиуса r и массы M по порядку величины равна:
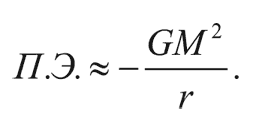
Внутренняя энергия в единице объема пропорциональна давлению р, поэтому полную внутреннюю энергию можно оценить как:
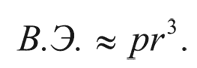
Гравитационные силы будут преобладать над силами давления, если
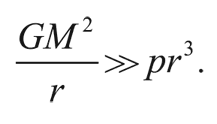
Но для заданной плотности ρ мы можем выразить r через M, пользуясь соотношением
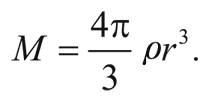
Таким образом, условие гравитационного скучивания приобретает вид
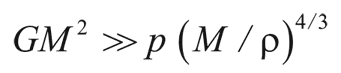
или по-другому:
М >> Мj,
где MJ (с точностью до несущественного численного множителя) называется массой Джинса:
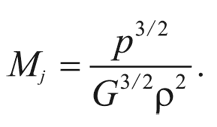
Например, непосредственно перед рекомбинацией водорода плотность равнялась 9,9 × 10¯22 г/см 3 (см. математическую заметку 3 на с. 237), а давление:
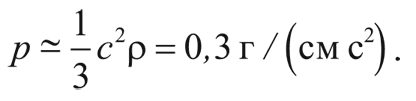
Следовательно, масса Джинса была:

Интересно отметить, что крупные шаровые скопления в нашей Галактике имеют примерно такую же массу.
Заметка 6. Температура и плотность нейтрино
Если тепловое равновесие не нарушается, в системе сохраняется физическая величина, известная как энтропия. Для наших целей достаточно будет воспользоваться приближенной формулой для энтропии S в единице объема при температуре T:
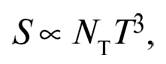
где ΝΤ – эффективное число сортов частиц, находящихся в тепловом равновесии, температурный порог которых ниже Τ. Чтобы сохранить энтропию на постоянном уровне, надо, чтобы S была обратно пропорциональна кубу размера Вселенной. Другими словами, если R – расстояние между любой парой типичных галактик, то:
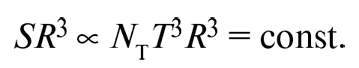
Незадолго до аннигиляции электронов и позитронов (при температуре около 5 × 109 K) нейтрино и антинейтрино уже вышли из теплового контакта с веществом во Вселенной, поэтому единственными частицами в тепловой бане оставались электрон, позитрон и фотон. Возьмем из таблицы I на с. 212 полное эффективное число сортов частиц до аннигиляции:
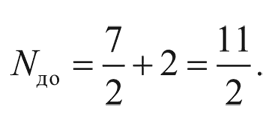
После того как в четвертом стоп-кадре электроны и позитроны аннигилировали, во Вселенной стали преобладать фотоны. Таким образом, число сортов стало:
Nпосле = 2.
Из сохранения энтропии следует, что:
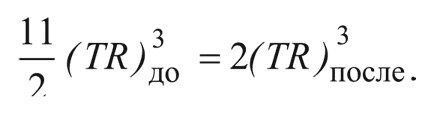
То есть тепло, выделившееся в процессе аннигиляции электронов и позитронов, приводит к повышению величины TR на коэффициент:
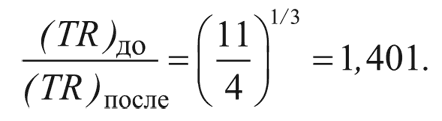
До аннигиляции электронов с позитронами температура нейтрино Τ была равна температуре фотонов Τ. Но затем Τv начала падать просто как 1/R, поэтому в любой последующий момент времени TvR равно значению TR до аннигиляции:
(TvR)после = (TvR)до = (TvR)до.
Отсюда заключаем: после завершения процесса аннигиляции температура фотонов превышает температуру нейтрино на коэффициент:
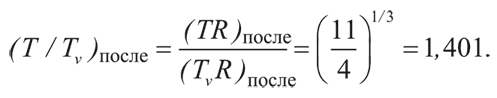
Хотя нейтрино и антинейтрино вышли из теплового равновесия, они вносят существенный вклад в полную плотность энергии. Эффективное число сортов нейтрино равно 7/2, т. е. 7/4 от числа степеней свободы фотона. (Фотон может находиться в двух состояниях с разным спином.) А температура нейтрино в четвертой степени, наоборот, в (4/11) 4/3 раза меньше температуры фотонов в четвертой степени. Соответственно отношение плотности энергии нейтрино и антинейтрино к плотности энергии фотонов равно:
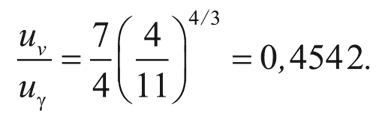
Из закона Стефана – Больцмана (см. главу 3) следует, что при температуре фотонов T плотность энергии фотонов есть:
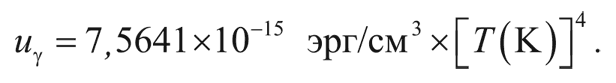
Таким образом, полная плотность энергии после аннигиляции электронов и позитронов равна:
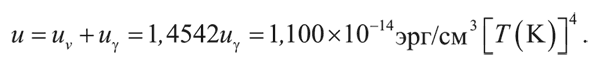
Эту величину можно пересчитать в массовую плотность, разделив первую на квадрат скорости света: