Математическое приложение

Эти заметки предназначены для читателя, желающего вникнуть в математические выкладки, на которых зиждется описательное изложение материала данной книги. Их можно пропустить без ущерба для понимания сути.

Заметка 1. Эффект Доплера

Пусть гребни волны испускаются источником света через равные промежутки времени T. Если он удаляется от наблюдателя со скоростью V, то за время T, разделяющее два последовательных гребня, источник пройдет расстояние VT. Чтобы достичь наблюдателя, волна должна затратить дополнительное время VT/c, где с – скорость света. Таким образом, промежуток времени, через который наблюдатель регистрирует соседние гребни, равен

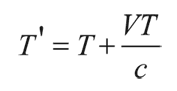
Длина волны испущенного света:

λ = cT.

Длина волны принимаемого света:

λ' = cT'.

Отношение этих длин:

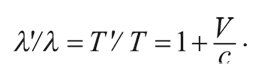
Предложенный вывод применим к случаю, когда источник движется по направлению к наблюдателю, за исключением того, что V меняется на – V. (Все вышесказанное справедливо в отношении любого волнового сигнала – не обязательно света.)

Например, скопления галактик в Деве удаляются от нас со скоростью 1000 км/с. Скорость света – 300 тысяч км/с. Следовательно, длина волны λ' любой из линий в спектре скопления больше ее номинального значения на коэффициент

Заметка 2. Критическая плотность

Рассмотрим сферу радиуса R, заполненную галактиками. (Для наших целей R должно быть больше расстояния между скоплениями галактик, но меньше длины, сравнимой с размером Вселенной в целом.) Масса, заключенная в этой сфере, равна ее объему, умноженному на плотность вещества ρ:

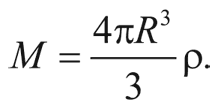
Согласно Ньютоновой теории всемирного тяготения, потенциальная энергия типичной галактики на поверхности этой сферы есть:

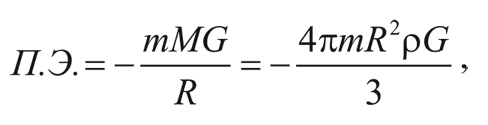
где m – масса галактики, а G – гравитационная постоянная Ньютона:

G = 6,67×10^–8 см ³/(gm с ²).

Скорость этой галактики можно найти из закона Хаббла:

V = HR,

где H – постоянная Хаббла. Таким образом, кинетическая энергия равна:

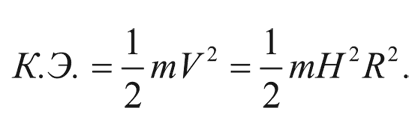
Полная энергия галактики – это сумма кинетической и потенциальной энергии:

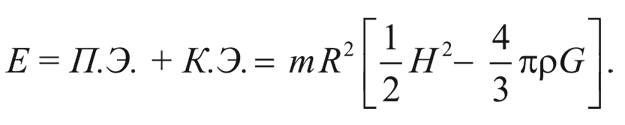
При расширении Вселенной эта величина должна оставаться неизменной.

Если E отрицательна, то галактика никогда не уйдет на бесконечность, поскольку на больших расстояниях потенциальной энергией можно пренебречь. Тогда полная энергия оказывается практически равной кинетической, а та, в свою очередь, всегда положительна. С другой стороны, если E положительна, то галактика может достичь бесконечности с некоторым запасом кинетической энергии. Таким образом, энергия E галактики, движущейся со скоростью убегания, по определению равна нулю. Откуда следует, что:

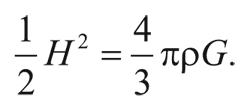
Другими словами, плотность должна равняться:

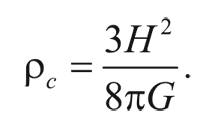
Это и есть критическая плотность. (Хотя мы получили этот результат в рамках ньютоновской физики, он применим и тогда, когда вещество во Вселенной обладает релятивистскими скоростями. Под ρ в таком случае понимается полная плотность энергии, деленная на с ².)

Например, если взять общепринятое сегодня значение постоянной Хаббла (15 км/с на миллион световых лет), то, учитывая, что в световом годе 9,46 × 10¹² километров, получим:

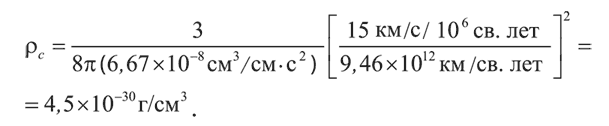
В одном грамме содержится 6,02 × 10²³ нуклонов. Соответственно это значение критической плотности соответствует 2,7 × 10^–6 нуклонам на кубический сантиметр, или 0,0027 частицы на литр.

Заметка 3. Оценки времени расширения

Рассмотрим теперь, как параметры Вселенной меняются со временем. Допустим, в момент времени t типичная галактика массой m находится на расстоянии R(t) от произвольно выбранного центра – например, от нашей Галактики. В предыдущей заметке мы показали, что полная (кинетическая и потенциальная) энергия такой галактики равна:

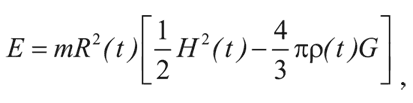
где H(t) и ρ(t) – значения постоянной Хаббла и плотности вещества во Вселенной в момент времени t. Эта величина является постоянной. Однако мы скоро увидим, что ρ(t) при R(t) → 0 растет не медленнее, чем 1/R³(t), поэтому ρ(t) R²(t) растет не медленнее, чем 1/R(t), когда R(t) стремится к нулю. Чтобы результирующая энергия оставалась постоянной, два слагаемых в скобках должны быть почти равны. В итоге при R(t)→0 имеем:

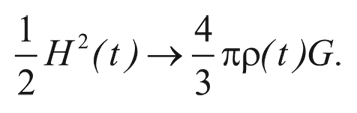
Характерное время расширения Вселенной есть величина, обратная постоянной Хаббла, т. е.:

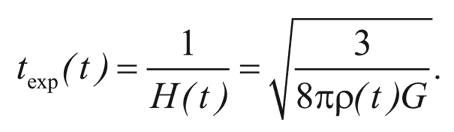
Например, в момент первого стоп-кадра в главе 5 плотность составляла 3,8 миллиарда грамм на кубический сантиметр. Таким образом, время расширения равнялось:

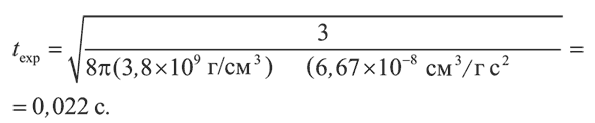
Зададимся вопросом: как ρ(t) зависит от R(t)? Если основной вклад в плотность вносят нуклоны (материально-доминированная стадия), то полная масса внутри сопутствующей сферы радиуса R(t) пропорциональна количеству нуклонов внутри этой сферы и, следовательно, не меняется:

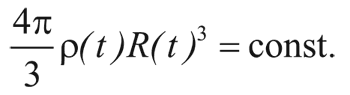
Следовательно, ρ(t) обратно пропорциональна R(t)³:

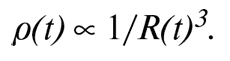
(Символ ∝ означает «пропорциональна».) Если же в плотности преобладает плотность (массовая) излучения (полученная из плотности энергии делением на скорость света в квадрате), что соответствует радиационно-доминированной эпохе, то p(t) пропорциональна четвертной степени температуры. Но температура меняется как 1/R(t), а значит, ρ(t) обратно пропорциональна R(t)⁴:

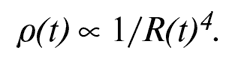
Чтобы одновременно учесть как материально-, так и радиационно-доминированную стадию, запишем этот результат в следующей форме:

Попутно заметим, что ρ(t), как и следовало ожидать, действительно расходится не медленнее, чем 1/R(t)³ при R(t) → 0.

Но скорость типичной галактики тогда равна:

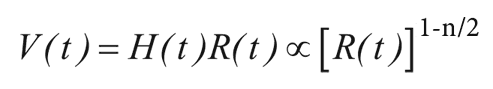
Из дифференциального исчисления хорошо известно, что если скорость пропорциональна какой-либо степени расстояния, то время, необходимое для перемещения из одной точки в другую, пропорционально изменению отношения расстояния к скорости. Говоря более точно, если V пропорциональна R(t)^1–n/2, то промежуток времени

Таким образом, каково бы ни было значение n, истекшее время пропорционально разности обратных корней из плотности.

Например, после аннигиляции электронов и позитронов в течение всей радиационно-доминированной эпохи плотность энергии имеет следующий вид (см. математическую заметку 6 на с. 249):

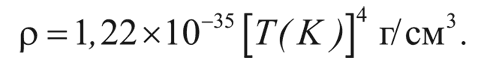
Кроме того, в последнем выражении п = 4. Таким образом, Вселенная охлаждается от 100 до 10 миллионов градусов за:

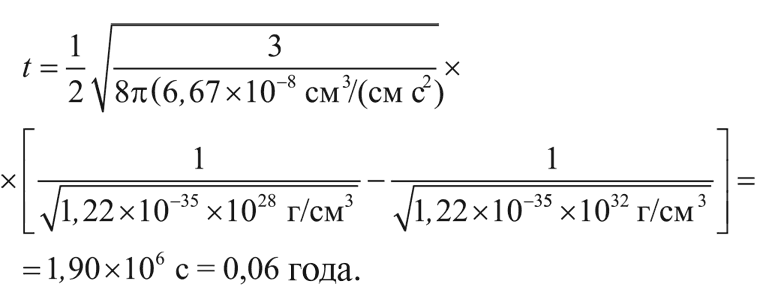
Полученный общий результат более прозрачно можно сформулировать так: промежуток времени, за который плотность падает до ρ (с величины, много большей, чем ρ), равен:

(Если ρ(t₂) > ρ(t₁), то вторым членом в формуле для t₁ – t₂ можно пренебречь.) Например, при температуре 3000 K массовая плотность фотонов и нейтрино равнялась:

ρ = 1,22 × 10^–35 × [3000]⁴ г/см³ = 9,9 × 10¯²² г/см³.

Это настолько мало по сравнению с плотностью при 10⁸ K (или 10⁷ K, или 10⁶ K), что время, за которое Вселенная охладится от очень высоких температур, царивших в первые мгновения ее жизни, до 3000 K, можно рассчитать (положив n = 4) следующим образом:

Мы показали, что промежуток времени, за которой плотность падает от экстремальных значений, имевших место в ранней Вселенной, до ρ пропорционален, а сама плотность ρ пропорциональна 1/Rⁿ. Время, следовательно, пропорционально R^n/2, или, что то же самое:

Эта формула остается в силе до тех пор, пока кинетическая и потенциальная энергии не упадут настолько, что достигнут одного порядка с их суммой – полной энергией.

Как было отмечено в главе 2, в любой момент времени t на расстоянии ct существует горизонт, отсекающий сигналы, которые еще не успели до нас дойти. Теперь мы увидели, что R(t) при t → 0 уменьшается медленнее, чем расстояние до горизонта. То есть в прошлом был момент, когда все «типичные» частицы находились за горизонтом.