25. Спин и его применение

Помимо заряда и массы элементарные частицы характеризуются третьей величиной чисто квантового происхождения – спином. Мы увидим, что это понятие можно уподобить существованию постоянного вращения частиц вокруг своей оси, что объясняет некоторые факты большого масштаба, такие как намагничивание материалов или поляризация света. Использование спина в технологиях будущего ждет широкий размах: в этой главе мы затронем область, предшествующую появлению квантовой информатики.

1. Основополагающее вращение

Постоянная Планка: момент импульса

Каждый из двух разделов современной физики, теория относительности и квантовая физика, построены вокруг фундаментальных констант: скорости света с и постоянной Планка h.

Безусловный характер этих констант – факт, подтвержденный опытом, а не теоретическое предсказание. Это даже выглядит удивительным по отношению к традициям классической физики. Возьмем пример со скоростью света. Сначала было определено понятие пространства (единица измерения – метр) и понятие времени (единица измерения – секунда), а потом понятие скорости – расстояния, пройденного за единицу времени. У скорости даже нет собственной единицы измерения, поскольку она выражается в метрах в секунду: это подтверждает идею, что речь идет о побочном продукте пространства и времени, как если бы речь шла о концепте менее фундаментальном. Между тем относительность полностью меняет данную парадигму: в следующей главе мы увидим, что расстояние, как и время, зависят от системы отсчета, а следовательно, являются понятиями относительными. Зато существует предельная непреодолимая скорость, которая всегда одна и та же для всех систем отсчета, а значит, является абсолютной. Из этого следует, что свет всегда распространяется с такой скоростью в вакууме, какой бы ни была система отсчета. В том, что природа ставит таким образом на пьедестал понятие света гораздо выше понятия пространства и времени, есть нечто интригующее для нашего классического мировоззрения.

То же самое с постоянной Планка. Какой физической величине она соответствует? Вопрос немного сложнее, чем в случае со скоростью света. Чтобы на него ответить, мы можем воспользоваться связью энергии с частицей: E = hv (где v – частота колебаний волны-частицы). Мы видели, что понятие энергии представляет собой движение или потенциальность движения. То есть это «эффективная» кинетическая энергия или потенциальная: с определением E_c = ½mυ² мы констатируем, что энергия выражается в кг ⋅ (м/с)². Так, постоянная Планка h = E/V = E ⋅ T (вводится понятие периода Т колебания волны) выражается в кг ⋅ м²/с.

Это немного сложная единица: если скорость света вводила в игру понятие расстояния и времени, постоянная Планка также вводит понятие массы. Между тем это довольно известная величина в классической физике: речь идет о моменте импульса (глава 6).

Кинетический момент был введен, когда мы изучали свойства объекта, вращающегося вокруг своей оси. В частности, если объект с массой m описывает окружность со скоростью v вокруг оси, расположенной на расстоянии l, его момент импульса по определению равен mvl. Таким образом, момент импульса выражается в кг ⋅ м²/с, как постоянная Планка.

Вот довольно неожиданный результат: на самом фундаментальном уровне природа представляется квантовой в отношении момента импульса. Как будто вращение вокруг своей оси является основополагающим свойством в микроскопическом масштабе, свойством частиц. Если постоянная Планка исторически была введена, чтобы представить квантование энергии (E = hv), она выглядит менее фундаментальной, поскольку зависит от частоты v: можно получить любую энергию E, заставив измениться частоту v частицы-волны. Напротив, постоянная h, взятая отдельно, представляет собой безупречный момент импульса, независимый от всякого другого физического параметра. Это предполагает, что можно получить фотон или электрон любой энергии, но не любого момента импульса. Понятие момента импульса, столь нелогичное, выглядит величиной, от которой происходят все остальные.

Эти несколько абстрактные рассуждения предполагают, что все частицы должны были бы характеризоваться чем-то вроде пожизненного «фундаментального вращения», которое мы назовем «спин» (в переводе с английского «вращаться»). Опыты подтвердят это предположение.

Спин фотона

Фотон – это электромагнитная волна, но мы видели, что такие волны характеризовались их состоянием поляризации (глава 20). Если электрические и магнитные поля колеблются вдоль фиксированной оси, речь идет о прямолинейной поляризации. Если они вращаются вокруг оси, речь идет о круговой поляризации. Наконец, эллиптическая поляризация является промежуточным звеном между прямолинейной и круговой.

Мы видели, что любую волну можно увидеть как наложение волн или прямолинейных, или круговых. Так, фотон, неделимая электромагнитная волна, должен характеризоваться состоянием поляризации: или круговой, или прямолинейной. В первом случае это значит, что фотон, перемещаясь, вращается вокруг своей оси, порождая вращение своего электромагнитного поля. Иными словами, он должен обладать присущим ему моментом импульса. Во втором случае фотон всегда должен ориентироваться на одну ось.

Опыт позволяет легко определить, какая из гипотез верна: в самом деле, мы видели, что поглощение прямолинейной волны поляризатором зависит от угла ее наклона. И напротив, круговая волна поглощается одинаково, независимо от направления поляризатора, поскольку электрическое поле ликвидирует все направления во время своего кругового вращения.

Опыт неоспоримый: фотон поляризуется круговым способом, а это означает, что, передвигаясь, он вращается вокруг своей оси. Значит, он обладает собственным моментом импульса, который можно измерить: он равен h/2π. Эта величина так важна, что физики обозначают ее ћ: по определению ћ = h/2π. То есть все фотоны Вселенной обладают одним и тем же собственным моментом импульса, равным ћ, какова бы ни была их частота и энергия. Это настолько фундаментальная величина, что физики сделали из нее характеризующую величину спина, то есть фотон обладает спином, равным 1. Другими словами, спин, равный 1, соответствует кинетическому моменту, равному ћ.

Можно задаться вопросом, как фотону удается всегда сохранять один и тот же спин, тогда как частота его колебания может меняться. В случае с круговой поляризацией электромагнитное поле вращается вокруг оси, а частота соответствует числу оборотов в секунду. Если удвоить частоту, это означает, что фотон вращается вдвое быстрее вокруг своей оси: его спин должен был бы увеличиться.

Однако момент импульса зависит не только от скорости вращения: в частности, мы видели, что он был равен mvl в случае с объектом, совершающим круговое движение. Если скорость вращения увеличивается, момент импульса может остаться постоянным при условии, что радиус r пройденного круга уменьшается.

Представим фотон в виде вращающейся сферы: если частота увеличивается, это значит, что сфера быстрее вращается вокруг своей оси, то есть радиус сферы уменьшается, поскольку спин должен быть равен 1. Нужно признать, что такие «сферические фотоны» естественным образом сжимаются, когда их стараются заставить вращаться быстрее.

Необходимо, однако, понимать пределы такого изображения фотона в форме сферы. Понятие частоты колебания имеет смысл только для фотона в форме волны, тогда как наша сферическая модель соответствует фотону-корпускуле. Между тем фотон существует либо как волна, либо как корпускула, но никогда и то и другое одновременно: в этом состоит тонкость корпускулярно-волнового дуализма.

Здесь мы поднимаем сложные вопросы понятия реальности, к которым мы уже привыкли благодаря квантовой физике: некоторые квантовые явления не имеют классических аналогов, и использовать классическую картинку (например, сферического объекта) здесь нельзя. И все-таки это неизбежная необходимость, если мы хотим выйти за пределы математической абстракции, чтобы представить себе, что происходит на микроскопическом уровне. В этом смысле изображение «фотона-волны», который превращается в «фотон – сферическую вращающуюся корпускулу» в момент его обнаружения, остается, без сомнения, наиболее соответствующим тому, что происходит на самом деле.

Спин электрона

Аналогии между фотоном и электроном позволили Луи де Бройлю догадаться о волновой природе электронов: как и фотон, электрон является волной (облаком), которая превращается в корпускулу, когда его пытаются обнаружить. Поскольку фотоны-корпускулы обладают собственным моментом импульса (спином), естественно предположить, что электроны могут тоже его иметь.

Возьмем один электрон в атоме: мы видели, что, будучи волной, он был одновременно повсюду, как облако. Мы также видели, что этот электрон может переходить с одной орбитали на другую, излучая или поглощая фотон. На практике такую смену орбиталей позволяет электромагнитная сила; но излучение волны возможно лишь при условии, что электрон вращается вокруг ядра. Иначе говоря, он должен обладать моментом импульса, который называется орбитальным моментом.

Напомним, что понятие траектории не имеет никакого смысла для электрона-корпускулы, то есть этот орбитальный момент относится к электрону-волне. В каком-то смысле вокруг ядра вращается электронное облако.

Напрашивается вывод: орбитальный момент электрона никак не связан со спином, поскольку соответствует движению электрона вокруг ядра, а не вокруг своей оси. Ничто не указывает на то, что электрон обладает собственным моментом импульса: для этого нужно было бы, чтобы электроны-корпускулы вращались вокруг своей оси. Представим электрон в его атоме: пока не стремятся обнаружить его местоположение, он является «вращающимся облаком», которое занимает все пространство атома. Как только мы хотим узнать, где он находится, электрон становится частицей, расположенной в определенном месте атома. Если у него есть спин, тогда эта частица должна продолжить вращаться вокруг своей оси: обнаружение исказило его орбитальный момент, уничтожив волну, но не исказило его собственный момент импульса, который сохраняется даже после превращения в частицу.

Как узнать, обладает ли электрон спином? Тот факт, что он ведет себя как заряженная частица, значительно все упрощает: в самом деле, всякая заряженная вращающаяся сфера создает магнитное поле, которое легко обнаружить. Другими словами, электрон, обладающий спином, должен вести себя как маленький магнит.

Опыт был проведен в 1925 г. Штерном и Герлахом: они послали атомы серебра к магнитам. Идея была проста: если атомы серебра сами являются маленькими магнитами, они должны отклониться в присутствии другого магнита (два одинаковых полюса отталкиваются, два полюса с противоположным знаком притягиваются).

Штерн и Герлах обнаружили, что половина атомов серебра отклонилась вверх, а половина вниз. Иными словами, атомы серебра повели себя именно как маленькие магниты: половина с северным полюсом направилась вверх, другая половина с северным полюсом направилась вниз.

Орбитальный момент не может объяснить наблюдаемое отклонение: у электронов наверняка должен быть дополнительный, присущий им кинетический момент, который равен ћ/2. Иными словами, опыт показывает, что электроны действительно имеют спин, равный ½, то есть наполовину меньше, чем у фотона.

Именно это свойство электронов вращаться вокруг своей оси позволяет объяснить существование магнитов: электроны-корпускулы являются малюсенькими магнитами, что объясняет, почему некоторые атомы (называемые парамагнетиками) также являются маленькими магнитами и, соответственно, некоторые вещества (ферромагнетики) образуют большие магниты. В главе 14 мы говорили, что способность некоторых веществ намагничиваться происходит из-за движения заряженных частиц внутри атомов. Мы видим, что в основном речь идет о вращении электронов вокруг собственной оси.

Удивительные свойства спина

Опыт Штерна и Герлаха не только позволил открыть существование спина электрона. Он также выявил некоторые поразительные факты относительно природы спина, стоящие в одном ряду с другими удивительными свойствами квантовой физики, которые мы уже описывали. Идея проста: представим электроны-корпускулы в виде маленьких вращающихся сфер. У оси вращения нет никаких причин быть направленной в какую-то определенную сторону: следовательно, каждый электрон должен иметь свою ось вращения. У некоторых северный полюс должен быть направлен вверх, у других вниз, у третьих вправо, у четвертых влево, у пятых по диагонали и т. д. Что же должно произойти во время опыта Штерна и Герлаха (➙ рис. 25.1)? Электроны, чей северный полюс направлен вверх, должны отклониться вверх из-за действия магнитной силы. Электроны с северным полюсом, направленным вниз, должны отклониться вниз. Те, чей полюс направлен вправо или влево, не должны отклоняться. Электроны с диагональным северным полюсом представляют собой промежуточный этап: чем больше полюс электрона-магнита отклонен от вертикали, тем меньше отклоняется электрон.

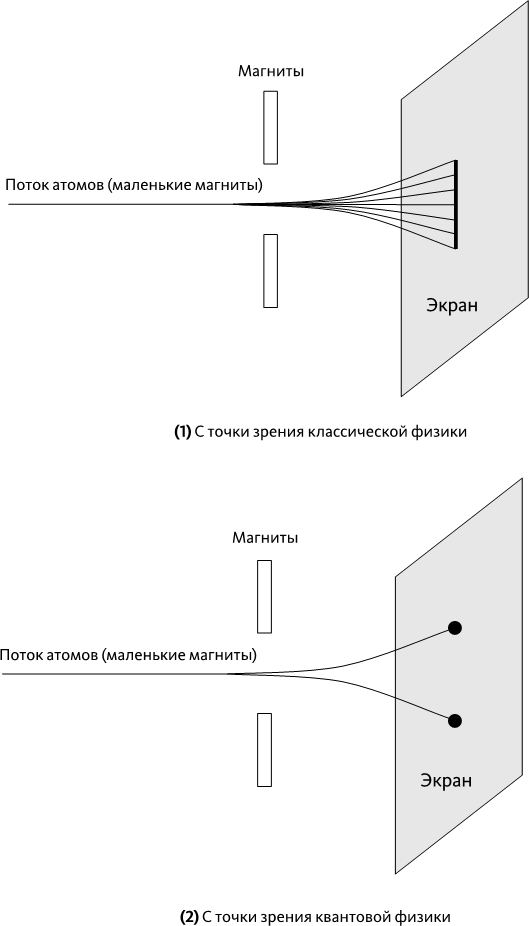
Рис. 25.1 – Отклонение электронов под действием магнитов

Из-за спина электронов атомы серебра ведут себя как маленькие магниты, ориентированные каждый в свою сторону. С точки зрения классической физики (1), каждый атом должен был бы отклониться в определенную сторону согласно направлению своей оси север – юг, вызвав на экране появление вертикальной черты. На практике мы наблюдаем лишь две точки на экране (2), как если бы все атомы были направлены вертикально (половина вверх, половина вниз).

В итоге, сложив вместе все электроны, мы должны получить очень разные углы отклонения, и на экране должна появиться вертикальная прямая, соответствующая всем этим точкам касания. Между тем Штерн и Герлах наблюдали лишь две точки на экране – одну сверху, другую снизу. В этом опыте все происходит так, как если бы все электроны-магниты были вертикальными: у половины северный полюс направлен вверх, у другой половины вниз. В частности, нет ни одного горизонтального электрона-магнита, поскольку нет ни одного центрального пятна, соответствующего отсутствию отклонения.

Есть еще нечто более странное: направим теперь эти электроны между полюсами горизонтального магнита. Поскольку все эти электроны являются вертикальными магнитами, ни один из них не должен отклониться под действием этого горизонтального магнита. Между тем мы, напротив, наблюдаем, что все они отклонились: половина направо, половина налево. Это значит, что на этот раз все электроны-магниты горизонтальны, хотя они те же самые, что и раньше. Перед нами настоящий парадокс: вертикальные или горизонтальные электроны-магниты? Опыт показывает, что они и те и другие сразу!

Вывод по меньшей мере странный: электроны вращаются во всех направлениях одновременно! Мы видим, что изображение электрона-корпускулы в виде вращающейся сферы становится еще более проблематичным: как можно себе представить сферу, обладающую одновременно бесконечным числом осей вращения? Более того, мы видим, что в момент измерения это множество осей вращения внезапно принимает определенную структуру и выбирает некое предпочтительное направление вращения.

Этот факт не такой уж новый: мы уже видели подобное в опыте Юнга. Пока мы не стремимся обнаружить местоположение электрона, он находится одновременно всюду (если это волна), объясняя феномен интерференции. Но как только мы пытаемся его обнаружить, он мгновенно концентрируется в определенной точке пространства (это частица). Аналогично пока мы не стремимся обнаружить спин электрона, он вращается во всех направлениях сразу. Но как только мы его измеряем, он мгновенно принимает определенное направление вращения.

Это открывает новые аспекты корпускулярно-волнового дуализма: он касается не только местоположения (рассеяние в пространстве в виде волны или локальной концентрации в виде частицы), но также других физических величин. Так, электрон вращается сразу во всех направлениях (аналог волны), пока спин не будет измерен (аналог частицы).

Более того, эти два типа корпускулярно-волновой трансформации не зависят друг от друга: если электрон концентрируется в частицу, когда речь идет о местоположении, он может оставаться в форме волны, когда речь идет о спине. В конечном итоге обе трансформации являются примером непредсказуемого характера природы: невозможно предсказать, в каком месте будет обнаружен электрон, так же как невозможно предсказать, в какую сторону он будет вращаться. В одной и той же физической ситуации электрон будет вращаться влево, а в другой – вправо. Нет никаких физических причин, чтобы объяснить этот выбор.

ФЕРМИОНЫ И БОЗОНЫ

Спин фотона равен 1, в то время как спин электрона равен ½. А как обстоит дело с другими частицами? Теория в соответствии с опытом предусматривает, что спин может быть только целым (как у фотона) или полуцелым (как у электрона). Это побудило физиков разделить элементарные частицы на две категории:

• Фермионы, обладающие полуцелым спином, то есть электрон является фермионом.

• Бозоны, обладающие целым спином: фотон, следовательно, является бозоном.

Подобное разделение отнюдь не искусственное: в самом деле, поведение частиц весьма различается в зависимости от того, бозон это или фермион. Это разграничение также связано с дихотомией, которая выглядит более логичной:

• Бозоны являются элементарными частицами взаимодействия. Например, гравитон, связанный с силой притяжения, и фотон, связанный с электромагнитной силой, являются бозонами. Таким образом, бозоны, в частности, являются элементарными частицами света.

• Фермионы являются элементарными частицами материи: атомы состоят из электронов, протонов и нейтронов – все они являются фермионами.

К понятию бозонов и фермионов мы вернемся в главе 28.

То же самое касается фотона: мы видели, что фотоны являются круговыми поляризованными волнами. Если мы пытаемся измерить эту поляризацию, у нас один шанс из двух увидеть, что фотон вращается влево, а также один шанс из двух увидеть его вращение вправо. Между тем до измерения фотон вращается в двух направлениях сразу. Более того, фотон не обладает никаким секретом, объясняющим, какое направление вращения он выберет, вправо или влево: в каком-то смысле в момент измерения информация «возникает из ниоткуда».