6. Неопределенность и индетерминизм

Классическая точка зрения

В классической физике формула ma^→; = F^→; управляет всей эволюцией Вселенной, где F^→; является суммой двух фундаментальных сил. Благодаря ей знание местоположения и скорости всех частиц Вселенной позволяет предсказать будущее с полной уверенностью: и действительно, это позволяет знать силу, приложенную к каждой частице, и из этого вывести их ускорение. Это позволяет вычислить новую скорость и местоположение в следующий момент и так далее. Таким образом, возможность точно знать местоположение и скорость лежат в основе детерминизма классической физики.

Как измерить две эти величины? В дальнейшем мы возьмем пример изолированной частицы, которая перемещается в пространстве с определенной скоростью. Сначала мы будем придерживаться точки зрения классической физики.

Измерение местоположения делается очень просто: достаточно использовать линейку… Измерение скорости дело более сложное: где скорость, там и движение, а где движение, там изменение времени. Таким образом, немедленно измерить скорость не получится: надо измерить изменение местоположения за два последовательных мгновения.

Если у нас достаточно точные измерительные приборы, можно выбрать два последовательных момента, настолько близких, насколько мы захотим. Так мы сможем узнать скорость частицы, с которой она преодолевает настолько малое расстояние, насколько мы этого хотим.

В конце концов, можно сразу узнать местоположение и скорость частицы с такой точностью, какой мы хотим (только неточность измерительных приборов может быть причиной неуверенности в измерениях).

Точка зрения квантовой физики

Посмотрим теперь на точку зрения квантовой физики, то есть на реальные вещи. Частица, которая перемещается, на этот раз является облаком, которое сконцентрируется в одной точке, как только мы попытаемся определить ее местоположение. Скорость частицы соответствует скорости облака.

Предположим, что облако имеет приблизительный диаметр 1 нанометр, а скорость – 1 нанометр в секунду (это та скорость, которую мы пытаемся измерить). Чтобы измерить скорость, можно произвести измерения в двух местах за два последовательных момента.

Рис. 23.8.а дает пример двух измерений с интервалом в секунду: каждый раз электрон найден в произвольном месте облака. Предположим, что во время первого измерения электрон находится в передней части облака, а во время второго – в задней: за одну секунду он преодолел как будто очень маленькую дистанцию. Скорость, измеренная таким способом, абсолютно не согласуется с реальной скоростью облака.

Как снизить неопределенность измерения, чтобы получить скорость, наиболее близкую к реальной? Просто увеличив временной интервал между двумя измерениями: рис. 23.8.b показывает два измерения за 10 секунд интервала. За это время облако прошло большое расстояние. Таким образом, местоположение электрона в облаке на момент обнаружения мало влияет на измерение пройденной дистанции. Из этого можно с большой точностью вывести скорость облака.

Проблема в том, что это дает лишь среднюю скорость в определенном интервале позиций. Это не дает абсолютно никакой информации о скорости частицы в определенном месте.

В конце концов, у нас есть выбор. Или мы определяем скорость на коротком интервале, то есть получаем точную информацию о местоположении, но в этом случае неопределенность скорости получается огромной (➙ рис. 23.8.а). Или мы с большой точностью измеряем скорость, и в этом случае интервал позиций должен быть очень большим, тогда сильно возрастает неопределенность местоположения (➙ рис. 23.8.b). Не существует способа измерить сразу скорость и местоположение с высокой точностью. Увеличение точности одной величины автоматически снижает точность другой.

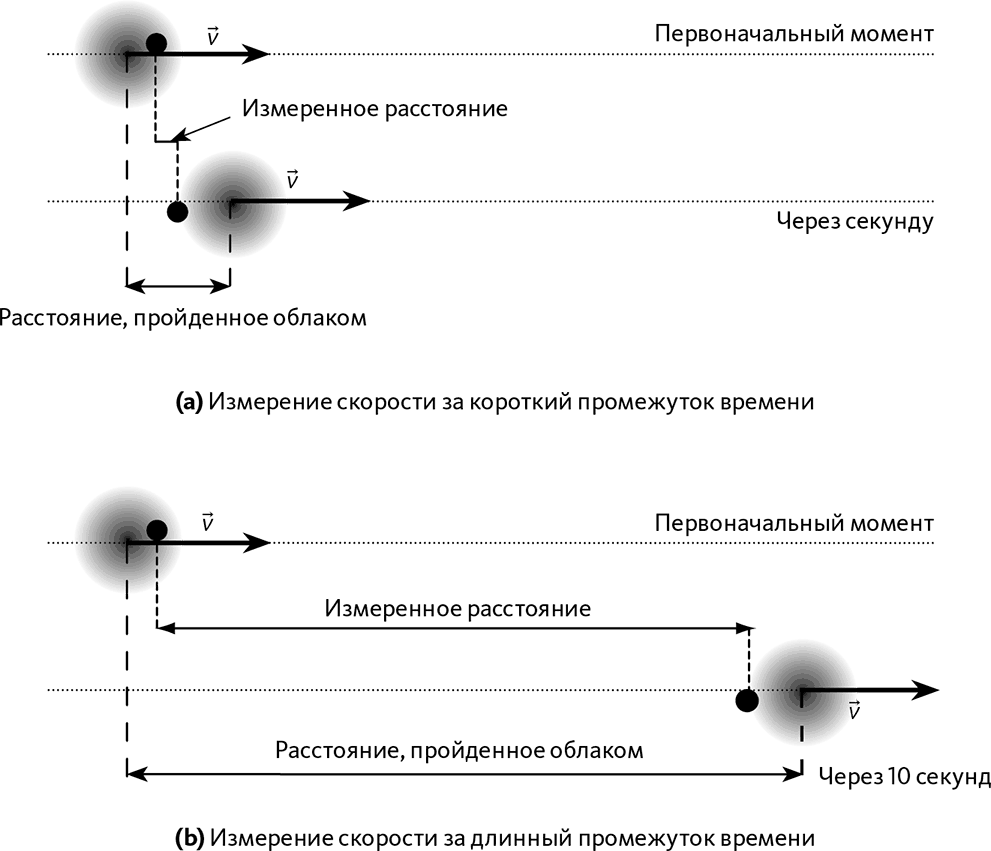
Рис. 23.8 – Неопределенность скорости и местоположения

Электрон перемещается слева направо. Черная точка представляет собой обнаружение электрона в определенный момент.

(а) – ошибка, допущенная в измерении скорости, значительная, потому что измерения производились на небольшой пройденной дистанции.

(b) – измерение скорости произошло с гораздо меньшей степенью неопределенности благодаря большему интервалу времени. В то же время мы получаем лишь среднюю скорость между двумя интервалами: у нас уже нет информации о скорости в определенном месте. Таким образом, неопределенность местоположения увеличивается, если мы пытаемся снизить неопределенность скорости.

Вернер Гейзенберг вывел уравнение, объединяющее две неопределенности: если Δx представляет собой неопределенность местоположения, а Δν неопределенность скорости, мы получаем mΔν ⋅ Δ x ≥ h/4π (для низких скоростей относительно скорости света).

Мы видим, что неопределенностью измерения скорости и местоположения управляет постоянная Планка. Это не должно удивлять: вспомним, что именно она определяет длину волны λ = h/mν, а значит, и размер облака. Чем больше облако, тем больше неопределенность.

Влияние на детерминизм

Можно подумать, что эта неопределенность связана с невозможностью сделать измерение и у частицы есть точные местоположение и скорость, даже если они неизмеряемы. На самом деле необходимо понять, что само понятие пары местоположение – скорость для частицы не имеет никакого смысла. Если рассматривать частицу как волну, ее точное местоположение определить невозможно, поскольку она рассеяна в пространстве. Если рассматривать частицу как точечную корпускулу, невозможно определить ее скорость, поскольку это точечное расположение имеет смысл только во время мгновенного обнаружения (когда проходит время, частица вновь становится волной).

В итоге мы только что по-другому заговорили об индетерминизме законов природы: неопределенность местоположения и скорости вызвано не неточностью измерительных приборов, она присуща фундаментальным законам квантовой физики. Само понятие пары местоположение – скорость, которое имело бы определенное значение, не имеет смысла. Сегодняшнее состояние Вселенной неопределимо по своей сути, ее будущее непредсказуемо.

НЕРАВЕНСТВО ВРЕМЯ – ЭНЕРГИЯ

Неравенство, обнаруженное между неопределенностью в скорости и местоположении, заключает в себе еще одно. Разница местоположений Δx напрямую связана с интервалом времени Δt. Кроме того, скорость частицы напрямую связана с ее энергией, то есть неопределенность скорости Δν связана с неопределенностью энергии ΔE. Из этого можно вывести следующее неравенство ΔE ⋅ Δ t ≥ h/4π.

По сути, невозможно измерить энергию частицы в определенный момент времени. Само понятие пары время – энергия, обладающей определенным значением, не имеет никакого смысла.

Квантовый вакуум

Принцип неопределенности Гейзенберга придает одно замечательное свойство самому вакууму.

Представим детектор частиц, чья разрешающая способность энергомасс-анализатора по энергии составляет 10 МэВ (МэВ – единица энергии, адаптированная для уровня частиц). Это значит, что этот детектор может выдавать значения, кратные 10 МэВ (10 МэВ, 20 МэВ, 30 МэВ… но не 15 МэВ). В частности, с таким детектором невозможно обнаружить электрон, обладающий только 1 МэВ, – детектор показал бы просто «0».

Чтобы обнаружить электрон, необходима бóльшая разрешающая способность, то есть меньшая неопределенность по энергии: неравенство Гейзенберга ΔE ⋅ Δ t ≥ h/4π показывает, что для такого измерения нужен больший промежуток времени. Если точнее, необходимо, чтобы Δ t > h/4πΔE. Предположим, что продолжительность жизни электрона

меньше этого срока: становится невозможно обнаружить его, какой бы датчик ни использовался. Таким образом, электрон невидим, и все происходит так, как будто его не существует: пространство кажется пустым.

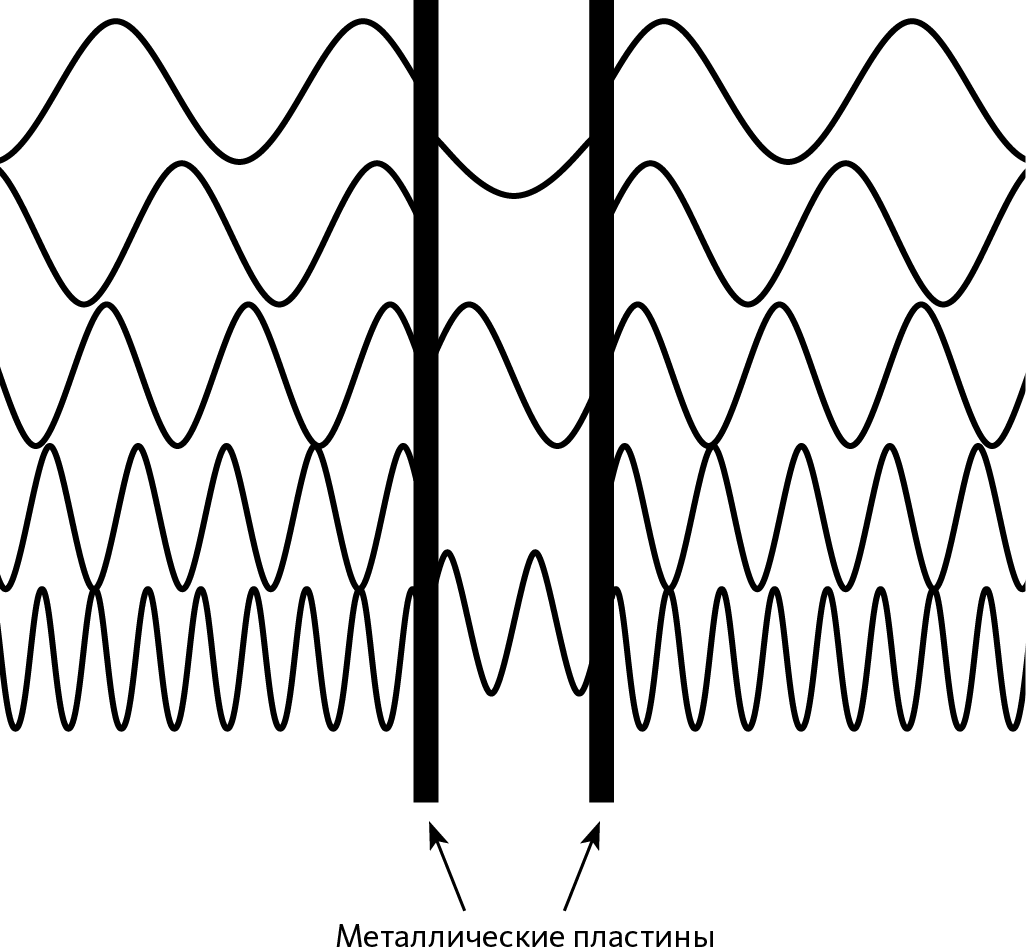
Рис. 23.9 – Селекция волн в полости

Мы представили виртуальные частицы снаружи и внутри полости в виде волн. Внутри могут существовать только волны, длина которых кратна двойной длине полости (λ = 2a/n): следовательно, виртуальных частиц гораздо больше снаружи, чем внутри, что повышает давление.

Этот факт затрагивает важный вопрос. Предположим, что мы создали абсолютный вакуум в некоей камере, убрав любые частицы (в том числе материю и свет). Действительно ли камера пуста или в ней есть частицы, которые невозможно обнаружить? Второе предположение согласуется с квантовой физикой: всегда существует вероятность присутствия частиц с малой продолжительностью жизни. Чем короче их существование, тем большей энергией они могут обладать, ускользая от детектора. Таким образом, не исключено, что даже абсолютный вакуум кишит неустойчивыми частицами, которые называют виртуальными.

Как проверить эту гипотезу? Мы могли бы сказать, что это невозможно, потому что эти виртуальные частицы невозможно обнаружить по определению. Но как часто бывает в физике, нет нужды обнаруживать их напрямую, чтобы констатировать их присутствие: их существование вызывает явления, которые могут быть измерены.

Наиболее впечатляющим из этих явлений является эффект Казимира. Возьмем две металлические пластины, параллельные друг другу и помещенные в абсолютный вакуум на очень маленьком расстоянии друг от друга. Представим, что на самом деле вакуум полон виртуальных частиц, которые распространяются в виде волн. Когда эти волны достигают металлической поверхности, они отражаются, «отскакивают» и летят в противоположную сторону. Как любая другая частица, они толкают металлические пластинки во время отскока, то есть на пластины оказывается определенное давление.

Поскольку виртуальные частицы представлены как внутри, так и снаружи, мы могли бы из этого заключить, что силы компенсируют друг друга. Но не следует забывать, что две пластины образуют полость, внутри которой могут существовать только волны определенной длины. Таким образом, внутри полости может существовать гораздо меньше волн, чем снаружи. Следует ожидать, что столкновения частиц с пластинами будут более многочисленны с внешней стороны, чем с внутренней. Следовательно, пластины должны приближаться друг к другу под действием этих ударов: пластины подвержены воздействию некой силы, даже когда помещены в абсолютный вакуум! В каком-то смысле абсолютный вакуум «еще более пуст» в пространстве между пластинами, чем за ними, что и провоцирует такое «притяжение». Более того, чем меньше расстояние между пластинами, тем меньше виртуальных частиц может там находиться, тем больше сила, приложенная к пластинам.

Эффект Казимира был предсказан физиком Хендриком Казимиром в 1948 г., а первое экспериментальное подтверждение получил в 1978 г. Этот опыт позволил подтвердить, что вакуум, который выглядит «абсолютно пустым», наполнен неопределяемыми частицами с очень кратким сроком существования.

ОГРОМНОЕ ВЛИЯНИЕ МАЛЮСЕНЬКИХ ЧАСТИЦ

Помимо эффекта Казимира существование этих частиц подтверждается и другими феноменами, которые мы рассмотрим в этой книге позднее. Скажем о двух из них.

Во Вселенной космический вакуум полон виртуальных частиц. Из-за их столкновения вся эта масса образует как бы газ под давлением, который стремится расшириться. Сам вакуум также должен быть подвержен чему-то вроде «отталкивающей силы», которая стремится расширить Вселенную. Между тем мы действительно обнаруживаем «отталкивающую силу вакуума», названную темной энергией, которая ускоряет расширение Вселенной (глава 27). На самом деле вычисления показывают, что виртуальные частицы далеко не способны объяснить наблюдаемое расширение; однако мы видим, что явления на микроскопическом уровне могут иметь реальные последствия в масштабе Вселенной.

Второе влияние, еще более важное, состоит в проявлении фундаментальных сил. Мы видели, что гравитация и электростатическая сила уменьшаются пропорционально квадрату расстояния в связи с тем, что пространство является трехмерным (глава 2). Однако с двумя другими фундаментальными силами все обстоит не так. Причина этого в том, что эти две силы действуют между очень близкими друг к другу частицами. Например, сильное взаимодействие происходит даже внутри протонов (глава 28). На таких микроскопических расстояниях «квантовая смесь», состоящая из виртуальных частиц, оказывает решающее влияние на взаимодействие, которое действует на «классический» распад, связанный с тремя измерениями пространства.

СЛЕДУЕТ ЗАПОМНИТЬ

• Частица материи ведет себя как волна, пока ее не обнаружат. Тогда она концентрируется в одной точке с вероятностью, которую определяет волна.

• Длина волны частицы нерелятивистской материи связана с постоянной Планка через выражение λ = h/mν (где m – масса частицы, а ν – ее скорость). Это, в частности, объясняет малый размер ядра атома относительно размера окружающих его электронов.

• Уравнение Шрёдингера заменяет второй закон Ньютона фундаментальным законом физики, который позволяет не только определить движение волн-частиц, но и их форму. В нашем масштабе волны выглядят точками, и тогда уравнение Шрёдингера отождествляется с вторым законом Ньютона.

• Из-за электростатической замкнутости ядра электрон, будучи волной, может принимать в атоме лишь строго определенные формы, называемые атомными орбиталями. Каждая форма соответствует определенной энергии.

• Когда электрон атома переходит к орбитали более низкой энергии, излучается фотон, выравнивающий разницу энергий. Таким образом, происходит излучение только волн определенной длины, что образует спектр излучения, состоящий из световых полос.

• Фотон поглощается атомом, если обладает достаточной энергией для того, чтобы отправить электрон на более энергетически высокую орбиталь. То есть поглощаются только волны определенной длины, что образует спектр поглощения, состоящий из темных полос.

• Благодаря своей волновой природе частица может преодолеть зону отталкивания, даже если она не обладает достаточной энергией с точки зрения классической физики. Это называется туннельным эффектом.

• Невозможно знать с большой точностью одновременно скорость частицы и ее местоположение: любое точное измерение одной из двух величин обязательно влечет за собой неопределенность другой величины. Эта неопределенность объясняет отсутствие детерминизма в законах Вселенной.

• Квантовая неопределенность позволяет вакууму быть заселенным частицами, не поддающимися обнаружению, которые называют «виртуальными частицами» и срок существования которых очень краток. Существование таких частиц, в свою очередь, приводит к явлениям, которые возможно измерить, например эффект Казимира.