2. Кинетическая энергия, температура и движение

Температура

Определение температуры

В предыдущем параграфе мы дали понять, что повышенная микроскопическая кинетическая энергия соответствовала повышенной температуре. Прежде чем идти дальше, очень важно уточнить, что же такое температура тела.

Исторически температура была связана с понятием тепла и холода (это также ее интуитивный смысл). Но поскольку ощущения тепла и холода весьма субъективны, пришлось найти средство для точного измерения этой самой температуры. Между тем люди заметили, что газы и металлы увеличиваются в объеме при нагревании – например, так ведет себя ртуть. Это изменение в объеме стали использовать для измерения температуры: в ртутном термометре чем выше столбик ртути, тем выше температура.

Также было замечено, что при определенном уровне давления лед превращался в жидкую воду при том же уровне ртути, то есть при той же температуре. То же самое при переходе воды в пар. Первыми двумя переменами состояния воспользовались, чтобы определить температурную шкалу: такой шкалой стала шкала Цельсия.

Было условлено, что при атмосферном давлении в 1 бар превращение воды в лед совершается при температуре 0 °C. Превращение воды в пар при 100 °C. Для любой другой температуры между 0 °C и 100 °C измеряют объем газа при давлении в 1 бар.

Возьмем реалистический пример: предположим, что при 0 °C объем газа составляет 73 л, а при 100 °C – 100 л: среднее значение между 100 л и 73 л – 86,5 л. Это значит, что если однажды объем газа составит 86,5 л, это будет соответствовать температуре в 50 °C (среднему значению между 0 °C и 100 °C). Мы видим, что определенный объем соответствует определенной температуре: значение температуры соответствует определенному значению объема.

В предыдущем примере, если объем газа будет меньше 73 л, значит, температура опустилась ниже 0 °C. А вот газ никогда не сможет иметь объем меньше 0 л… Что означает, что температура никогда не сможет опуститься ниже некоего минимального уровня, соответствующего этому объему в 0 л!

Простой подсчет поможет определить этот минимальный уровень: получается –273,15 °C (пытливый читатель может проверить это на предыдущем примере). Это значение называется абсолютным нулем, температура ни в коем случае не может быть ниже.

На основе этого вывода была введена новая температурная шкала, которой физики пользуются значительно чаще, чем шкалой Цельсия, – шкала Кельвина. По сути, это простое переложение значений шкалы Цельсия таким образом, что абсолютный нуль соответствует 0 °К (Кельвина), то есть 0 °К = –273,15 °C (абсолютный нуль). 273,15 °К соответствует 0 °C. 373,15 °К = 100 °C и так далее. Мы видим, что температура по Кельвину ни в коем случае не может быть отрицательной.

В дальнейшем, если не будет указано иное, по умолчанию будет использоваться температурная шкала Кельвина.

Связь между температурой, объемом и давлением

Определение температуры, каким мы вывели его в предыдущем параграфе, дает понять, что она не связана со скоростью молекул. Чтобы понять, откуда же берется эта связь, определим, от чего зависит описанная таким образом температура.

• Пункт первый. По определению температуры по Кельвину удвоенный объем газа соответствует удвоенной температуре (при атмосферном давлении), то есть при определенном давлении температура пропорциональна объему газа.

• Пункт второй. Заключим газ в твердый баллон с определенным объемом. Нагреем баллон: температура повысится, но на этот раз объем не сможет возрасти параллельно. Мы замечаем, что при этом увеличивается давление: если температура по Кельвину удваивается, то удваивается и давление газа.

Таким образом, при определенном объеме температура пропорциональна давлению газа (установлено опытным путем).

В более общем смысле опыты показывают, что температура T просто пропорциональна произведению давления P и объема газа V.

• Пункт третий. Предыдущий результат верен только для конкретного количества газа: если мы возьмем газа в два раза больше (при определенном давлении и температуре), очевидно, что занимаемый объем будет вдвое больше. Например, при давлении в 1 бар и температуре 20 °C объем воздуха в 20 л содержит вдвое больше молекул, чем объем в 10 л.

Таким образом, произведение PV пропорционально температуре не только T, но также количеству молекул n, которое содержит газ.

Мы запишем это как PV = nkT, где k соответствует константе пропорциональности, которая называется постоянной Больцмана.

ОБЪЯСНЕНИЕ АБСОЛЮТНОГО НУЛЯ

Экспериментальное выражение PV = nkT позволяет найти объяснение существованию минимальной температуры, ниже которой не существует.

И действительно, оно подразумевает, что при определенном объеме газа давление пропорционально температуре: иными словами, нулевая температура соответствует нулевому давлению. Между тем мы выяснили, что давление внутри газа происходит из-за столкновения молекул друг с другом: эти удары воздействуют с большой силой на любой предмет, который им встречается.

Если давление нулевое, значит, ударов больше нет, а это возможно, только если молекулы будут неподвижны. Но мы уже упоминали, что температура связана с этим движением молекул: если они неподвижны, такое состояние соответствует нулевой температуре. Имеется в виду, что ниже температура опуститься уже не может…

Предыдущее выражение записывается также 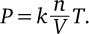Отношение n/V означает количество молекул на 1 м³ газа: это называется концентрацией, которую мы обозначим c. Таким образом, мы получаем PV = kcT: давление пропорционально произведению концентрациии температуры.

Это отношение, полученное опытным путем, будет очень полезно для понимания связи между температурой и микроскопической кинетической энергией, которая так нас интересует.

УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА

В выражении PV = nkT, которое мы получили, n представляет количество молекул газа в объеме V. Между тем число это огромно: мы уже говорили, что в кубическом сантиметре воздуха содержится десять миллиардов миллиардов молекул.

Именно поэтому мы предпочитаем выражать количество материи не в молекулах, а в молях. Моль представляет собой количество атомов, содержащихся в 12 г углерода, что соответствует огромному количеству материи: один моль воздуха содержит миллион миллиардов миллиардов молекул…

Если мы обозначим количество молей ν, предыдущее выражение приобретает вид: PV = νRT.

Изменилась только постоянная пропорциональности: из k она превратилась в R, которая называется универсальной газовой постоянной. А полученное выражение называется уравнением состояния идеального газа.

Почему «идеального»? Потому что это выражение не проверено опытным путем при очень высоком давлении по причинам, о которых мы расскажем в главе 11. Таким образом, когда можно использовать это выражение (что вполне устраивает физиков), говорят, что газ идеальный.

Отметим, что при атмосферном давлении воздух ведет себя совершенно как идеальный газ, что придает этому выражению большую значимость.

Выражение кинетической энергии

Теперь, когда мы прояснили ситуацию с определением температуры и ее зависимостей, вернемся к понятию энергии, а именно кинетической энергии.

Какое определение мы могли бы ей дать?

Очевидно, что в определении кинетической энергии должна присутствовать скорость: чем быстрее мы шагаем, тем больше у нас энергии. Но в игру вступает и другой параметр.

Выстрелите ядром из пушки: оно может пробить стену. Выстрелите теннисным шариком с той же скоростью: пробить стену будет гораздо сложнее. Мы интуитивно чувствуем, что при одинаковой скорости теннисный шарик обладает меньшей энергией, чем пушечное ядро. Причина в том, что ядро обладает гораздо большей инертностью (= массой), чем шарик: после выстрела ему трудно будет остановиться. Таким образом, инертная масса тоже должна быть упомянута в определении кинетической энергии.

Мы могли бы выразить кинетическую энергию в виде E_K = mν (где m – масса объекта, а ν – скорость). Но нужно учесть еще одно обязательное правило, которое мы себе установили: чтобы соответствовать интуитивному смыслу, кинетическая энергия должна быть связана с понятием температуры.

Однако можно показать, что температура пропорциональна mν², где ν² – квадрат средней скорости всех молекул тела, которое не обладает общим движением (доказательство этого довольно сложно, мы вынесли его во врезку ниже). Именно поэтому мы выразим кинетическую энергию объекта с массой m и скоростью ν следующим образом E_K = ½mν².

ТЕМПЕРАТУРА И ДВИЖЕНИЕ МОЛЕКУЛ

Чтобы понять связь между температурой и скоростью молекул, необходимо совершить путешествие в микромир. Мы ограничимся примером газа со стандартным давлением окружающей среды. Более того, предположим, что этот газ неподвижен, то есть не подвержен макроскопическому движению (= нет ветра).

Опытным путем мы уже установили связь между температурой и давлением, то есть остается определить связь между давлением и скоростью молекул, чтобы вывести из нее связь между температурой и скоростью этих молекул.

Сразу уточним важный факт: из-за бесконечных столкновений между собой молекулы перемещаются в самых разных направлениях с очень разными скоростями. То есть поведение газа на микроскопическом уровне весьма беспорядочно.

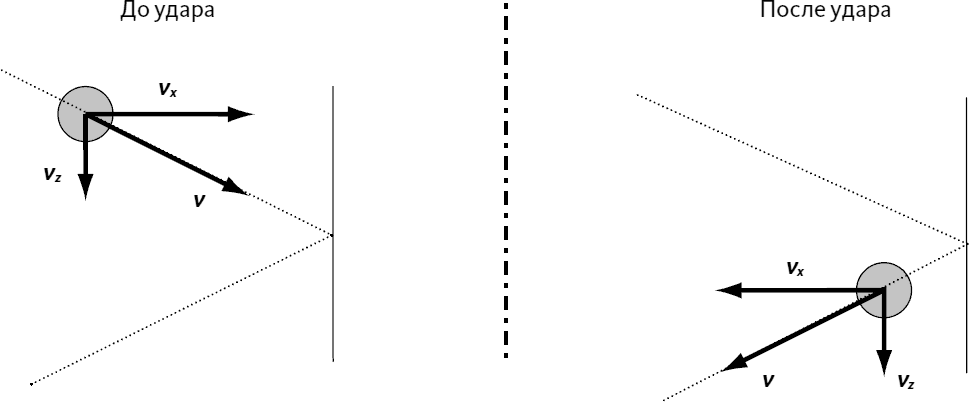
Предположим, что в газ поместили перегородку, каждая из молекул будет сталкиваться с ней с разной скоростью. В дальнейшем мы назовем ν_x составляющую скорости, вектор которой перпендикулярен перегородке (см. схему ниже). Именно эта составляющая будет управлять силой удара о перегородку. Чтобы немного упростить наши рассуждения, на первое время представим, что все молекулы обладают одной и той же скоростью ν_x.

Давление газа соответствует силе, с которой он действует на перегородку в 1 м² из-за столкновения с ней молекул. Чем больше молекул ударяет в перегородку за единицу времени, тем выше давление. Таким образом, давление пропорционально концентрации молекул и их скорости ν_x (потому что чем быстрее движутся молекулы, тем больше их ударяется в перегородку за единицу времени).

Чтобы определить давление, остается определить силу, с которой действует каждая из молекул: формула F^→; = ma нам в этом поможет. Она показывает, что сила пропорциональна массе молекулы и ее ускорению, то есть изменению ее скорости за единицу времени.

Однако во время удара молекула сначала затормозит из-за электростатического отталкивания, а потом полетит в другую сторону (см. схему ниже). На схеме мы видим, что меняется только составляющая скорости ν_x: сначала она переходит от ν_x к нулю, а потом меняет направление и возрастает от 0 до ν_x. То есть изменение этой составляющей во время удара составляет 2ν_x.

Подведем итог:

• каждая молекула действует с силой, пропорциональной ее массе и изменению скорости 2ν_x;

• количество молекул, действующих с этой силой, пропорционально их концентрации c и их скорости ν_x;

• таким образом, общее давление всех молекул пропорционально cmν² _x.

На практике каждая молекула имеет разную скорость, и ν² _x представляет собой средний квадрат скорости всех молекул.

Более того, поскольку движение молекул абсолютно хаотично, никакое из направлений нельзя считать основным, то есть составляющие скорости в трех направлениях пространства ν_x, ν_y, и ν_z равны. Однако математика говорит нам, что скорость удовлетворяет выражению: ν² = ν² _x + ν² _y + ν² _z, то есть в данном случае ν² = 3ν² _x.

Отсюда следует, что общее давление просто пропорционально cmν². Скорость ν называется средней квадратичной скоростью молекул.

Но что мы видим благодаря опыту? Что давление P пропорционально cT (см. предыдущую часть). Таким образом, P пропорционально cmν² и пропорционально cT. Это значит, что температура T пропорциональна mν². Это можно записать как:

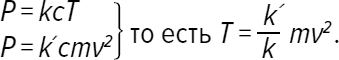
Температура пропорциональна средней кинетической энергии молекул, какой мы ее определили (E_K = ½mν²). Отметим, что формула одинакова для жидкостей и твердых тел.

Такое определение средней микроскопической кинетической энергии молекул характеризует температуру неподвижного тела, в то время как макроскопическая кинетическая энергия характеризует движение тела. Таким образом, кинетическая энергия одновременно связана с понятием температуры и понятием макроскопического движения.

Может возникнуть вопрос, что это за коэффициент ½, который мы ввели. Объяснение этого мы оставим до следующей главы. А пока что заметим, что этот фактор абсолютно не меняет физического смысла кинетической энергии.

ТЕМПЕРАТУРА ТВЕРДОГО ТЕЛА И ЖИДКОСТИ

В случае с газом мы убедились, что температура была связана со скоростью молекул. А как обстоит дело с твердыми телами и жидкостями? В твердых телах, например, молекулы и атомы не могут передвигаться на большие расстояния.

На самом деле даже в твердом теле атомы никогда не находятся в полном покое: несмотря на тесное соседство, они колеблются на определенном месте. То есть они обладают средней кинетической энергией, пропорциональной температуре твердого тела: чем теплее твердое тело, тем сильнее вибрируют составляющие его атомы.

Та же картина с жидкостью в состоянии покоя: молекулы могут перемещаться и, соответственно, обладают средней кинетической энергией, пропорциональной температуре жидкости.

Единица кинетической энергии – джоуль. Чтобы представить себе ее масштаб, заметим, что макроскопическая кинетическая энергия шагающего человека приблизительно равна 60 Дж. У машины, движущейся со скоростью 50 км/ч, около 100 000 Дж. Что же касается микроскопической кинетической энергии нашего тела, находящегося в покое (при температуре 37 °C), она составляет несколько десятков миллионов джоулей! То есть большая часть нашей энергии скрыта, поскольку представлена на микроскопическом уровне: движение молекулярного уровня гораздо более быстрое и повсеместное, чем в нашем масштабе.

ВРАЩЕНИЕ И КОЛЕБАНИЕ МОЛЕКУЛ

Выше мы говорили о том, что температура связана со средней кинетической энергией молекул. Мы говорили только о перемещении молекул, которое сообщает им кинетическую энергию. Но даже неподвижная молекула может обладать кинетической энергией.

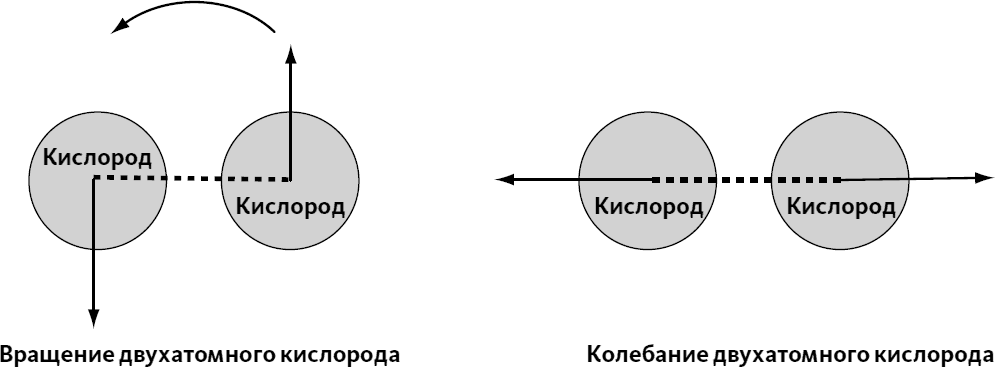
Для примера возьмем двухатомную молекулу кислорода О₂ (см. схему выше). Она может вращаться вокруг своей оси, то есть атомы кислорода могут обладать скоростью, даже если в целом молекула не перемещается. Более того, атомы кислорода могут вибрировать, то приближаясь, то удаляясь друг от друга, как если бы они были соединены пружиной (в реальности такой пружиной служит электростатическая сила).

Таким образом, к кинетической энергии перемещения нужно добавить кинетическую энергию вращения и колебания молекулы. Однако температура характеризует только перемещение по оси (это подтверждают рассуждения, которые позволили нам провести связь между температурой и скоростью молекул): следует ли из этого, что выражение пропорциональности между температурой и средней кинетической энергией молекул ложно?

Нет, потому что при столкновениях кинетическая энергия молекул естественно распределяется между перемещением, вращением и колебанием. Иными словами, чем больше средняя скорость молекул, тем более быстрое вращение и более сильное колебание вызывают столкновения. То есть при обычных температурах кинетическая энергия вращения и колебания пропорциональна кинетической энергии перемещения, а температура остается пропорциональна всей средней кинетической энергии молекул.