6. Осторожно! Мы вертимся!

До сих пор мы рассматривали движение объектов с определенным ускорением и скоростью. Но в действительности каждая точка объекта может обладать собственной скоростью и ускорением. Например, на вращающемся диске точка с краю движется с большой скоростью, а центр стоит на месте.

Здесь мы собираемся рассмотреть тот случай, когда предмет вертится вокруг своей оси (вращение), находясь при этом в движении (перемещение). Это поможет нам понять постепенное отдаление Луны, образование циклонов, устойчивость крутящейся юлы, едущего мотоцикла и многих других природных явлений.

Эта глава довольно сложная, и читатель, если пожелает, может ее пропустить без малейшего ущерба для понимания последующих разделов.

1. Запуск вращающегося объекта

Центр масс

Представим два положительно заряженных шара произвольного радиуса, изначально помещенные в некую точку пространства, которую назовем G. Предположим, что они «изолированы» от внешнего мира, то есть на систему из двух шаров не действует никакая внешняя сила. Однако оба шара отталкиваются друг от друга, то есть сила на них все-таки действует, но по отношению к системе она является «внутренней».

Как правило, какой бы ни была природа сил, сила, с которой предмет 1 действует на предмет 2, противоположна силе, с которой предмет 2 действует на предмет 1 (принцип взаимодействия), сумма внутренних сил равна нулю, потому что они гасят друг друга. В нашем случае электростатические силы равны и направлены в противоположные стороны (➙ рис. 6.1).

Представим, что шар В справа в три раза больше шара А слева: следовательно, ускорение шара В втрое меньше ускорения шара А, поскольку силы воздействия одинаковы a^→; = F^→; / m. То есть за определенное время шар В пройдет втрое меньшее расстояние, чем шар А (➙ рис. 6.1.b). Из этого следует, что отношение расстояний от точки G противоположно отношению масс: если В втрое тяжелее А, значит, он в три раза ближе к G, чем А.

Точка G называется центром инерции (см. врезку: там дано более развернутое определение). Ее отличительным свойством является отсутствие всякого ускорения при отсутствии внешней силы, как в нашем примере, где она остается неподвижной. Объекты могут удаляться или приближаться друг к другу, но отношение расстояний между ними всегда будет одинаковым.

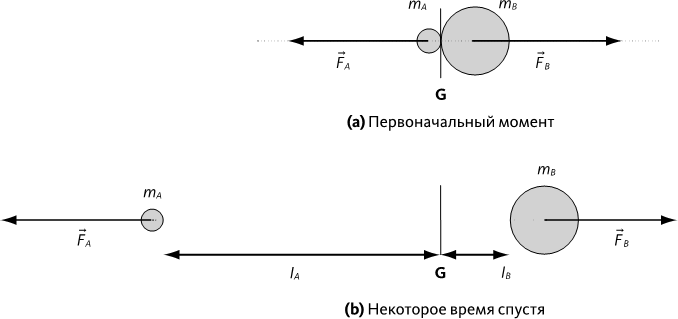
Рис. 6.1 – Центр масс изолированной системы Если m_B = 3m_A, то I_A = 3I_B

Момент силы

Условие перемещения объекта

Теперь соединим наши шары А и В стержнем незначительной массы: получилась несимметричная штанга. Теперь расстояние между А и В больше не изменится. На этот раз мы рассмотрим действие внешних сил.

ЦЕНТР ИНЕРЦИИ

В случае с нашими двумя шарами A и В центр инерции был определен как Это также записывается

В случае наличия нескольких масс m_i, расположенных в точке A_i, G также определяется как сумма то есть нулевая (говорят, что «G – барицентр точек A_i, зависимых от их массы m_i»).

Следовательно, положение G напрямую зависит от величины масс. Однако масса может представлять и инертную массу (для инерции), и гравитационную массу (для гравитации): по этой причине G с тем же успехом называется центром массы, центром тяжести или центром инерции.

На практике мы говорим о центре массы, когда речь идет о ее математическом определении (барицентр точек), о центре инерции, когда речь идет о движении («G не испытывает ускорения без воздействия внешней силы»), и о центре тяжести, когда речь идет о точке равновесия объекта (об этом мы расскажем позднее в этой же главе).

Говорят, что объект перемещается в системе отсчета, если он не вращается по отношению к этой системе отсчета. Например, на рис. 6.2 ось штанги не вращается по отношению к листку: то есть штанга перемещается по отношению к листку. Это значит, что в перемещающемся объекте все точки имеют одинаковый вектор скорости (одна скорость и одно направление). Что называется, объект перемещается целиком.

Из этого следует, что ускорение всех его точек должно быть одинаковым. В нашем примере ускорение шара А должно равняться ускорению шара В. Из этого мы заключаем, что отношение a^→; = F^→; / m должно быть идентичным для А и для В, то есть .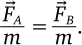

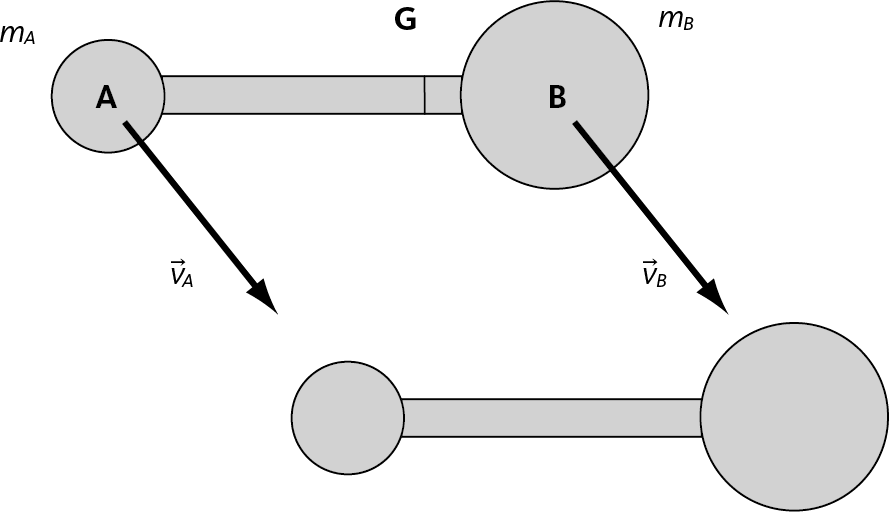
Рис. 6.2 – Перемещение штанги относительно листка

Если шар В в три раза тяжелее шара А, то для его перемещения должна быть приложена сила в три раза большая. Однако отношение масс обратно отношению расстояний от центра инерции G: обозначив эти расстояния l_A и l_B, мы получаем .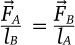

Другими словами, если шар В в три раза ближе к центру инерции, чем шар А, сила, действующая на В, должна быть в три раза больше, чем сила, действующая на А, чтобы наша штанга сдвинулась с места.

Определение момента силы

В этом отношении силы проявляют себя в форме векторов. В них можно выделить две составляющих:

• Одна из них направлена на ось шаров (➙ рис. 6.3). Она стремится придать ускорение шарам, направленное вдоль этой оси. Иначе говоря, эта составляющая ни в коем случае не может заставить ось вращаться. В то же время внутренние силы стремятся сохранить одинаковую дистанцию между шарами с помощью стержня.

• Другая составляющая действует перпендикулярно оси шаров. Только она может заставить штангу вращаться. Только внешние силы могут иметь составляющую с таким направлением: в дальнейшем мы будем рассматривать только ее (➙ рис. 6.3).

Обозначим α угол, под которым сила действует на ось двух шаров. Эта перпендикулярная составляющая силы записывается F ⋅ sin α. Если нас интересует только эта составляющая, отношение F^→;_A l_A = F^→;_B l_B, выведенное ранее, приобретает вид F^→;_A l_A sin α_A = F^→;_B l_B sin α_B.

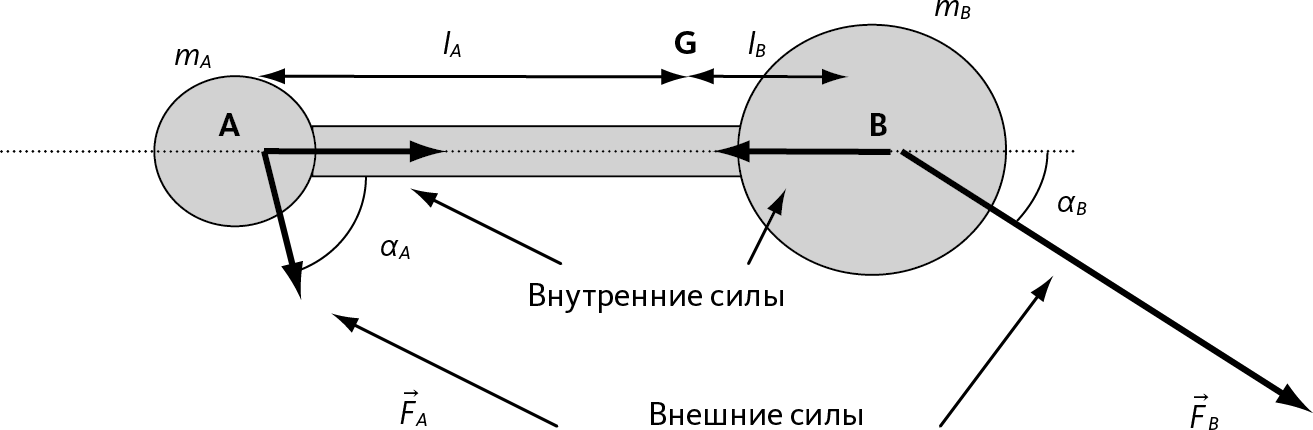
Рис. 6.3 – Силы, действующие на перемещающуюся штангу

Здесь мы обозначили внутренние силы, направленные вдоль оси по пунктирной линии, а также внешние силы. Чтобы вращения не было, составляющая силы, перпендикулярной оси, должна быть в три раза больше в В, чем в А, если масса m_B в три раза больше массы m_A. То есть F_B sin α_B = 3F_A sin α_A, если m_B = 3m_A.

Оно означает, что перпендикулярная оси штанги составляющая силы должна быть в три раза больше, если шар в три раза ближе к центру инерции. Если это условие не выполняется, значит, объект испытывает вращение (помимо перемещения): то есть вращается вокруг своей оси.

Иначе говоря, именно сравнение произведений Fl sin α каждого из двух шаров позволяет узнать, будет ли объект вращаться: произведение Fl sin α представляет собой возможность силы заставить объект вращаться. Его называют «моментом силы F». Поскольку l представляет здесь расстояние до центра инерции G, это называют «момент силы F по отношению к G».

Если момент силы в А больше момента силы в В, значит, объект заставит вращаться сила F_A: объект будет вращаться в направлении действия силы F_A. Поскольку сила вызывает ускорение, вращение будет постоянно ускоряться: как только моменты сил перестанут уравновешиваться, объект будет все быстрее вращаться вокруг своей оси.

Плечо рычага

Равновесие на острие

Теперь мы хотим установить нашу штангу на острие треугольного бруска так, чтобы она была в равновесии (➙ рис. 6.4). На какую точку мы должны ее положить?

На шары А и В действует одна сила: вес F = mg. Вес шара В в три раза больше веса шара А: F_B = 3F_A. В то же время В в три раза ближе к G, чем А, потому что его вес в три раза больше l = l_A / 3. То есть произведение F_A l_A равно произведению F_B l_B.

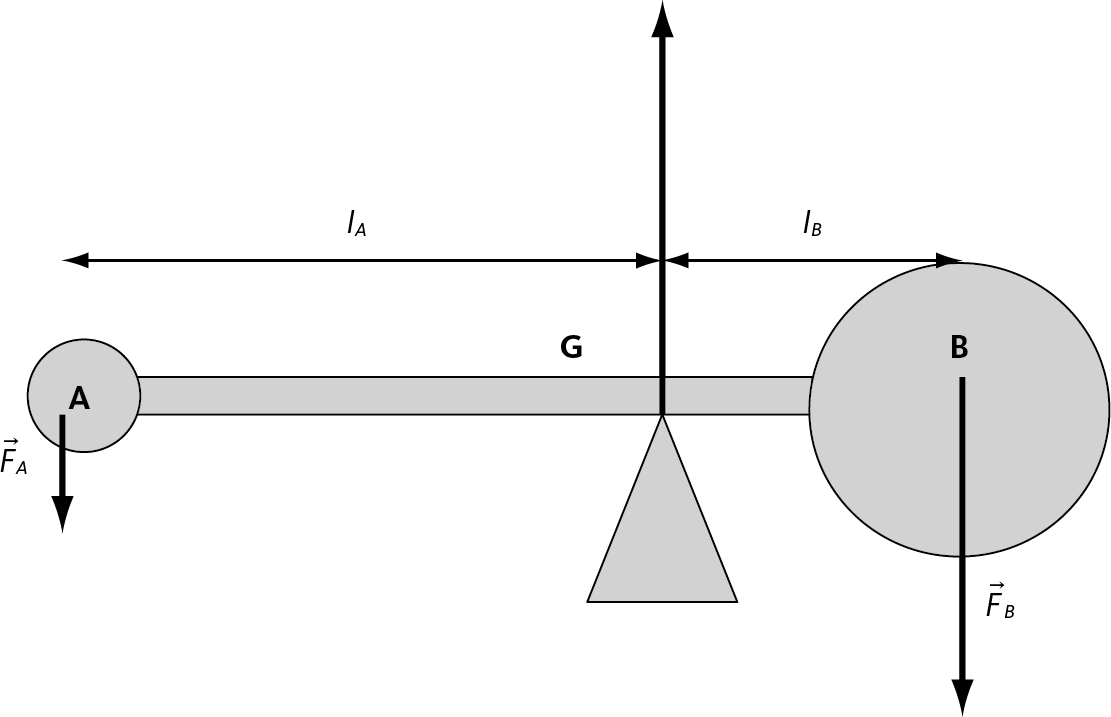
Рис. 6.4 – Штанга в равновесии на острие бруска

Силы перпендикулярны оси штанги: то есть выражения, которые мы ввели, sin α_A и sin α_B, равны 1. Таким образом, произведения F_A l_A и F_B l_B точно соответствуют моментам силы F_A и F_B по отношению к G: мы видим, что эти моменты компенсируют друг друга.

То есть вес не заставляет штангу вращаться. Это не удивительно: мы уже знаем, что все объекты падают с одинаковым ускорением. Следовательно, два шара, брошенные одновременно, будут падать с одинаковой скоростью: штанга падает, не вращаясь.

Однако, установив штангу на острие бруска, мы ввели в действие дополнительную силу: ту, с которой острие бруска действует на стержень. Мы хотим, чтобы штанга оставалась в равновесии: то есть мы не хотим, чтобы эта новая сила заставила штангу вращаться. Иными словами, момент этой силы по отношению к G должен равняться нулю. Произведение F ⋅ l должно равняться нулю: это значит, что острие бруска должно быть расположено в центре инерции G (чтобы было l = 0).

Увеличитель силы

Мы можем заменить штангу обычной доской, которая будет держаться на острие в равновесии (➙ рис. 6.5). Предположим, что с одного конца доска будет втрое длиннее, чем с другого. Мы увидели, что для сохранения равновесия нам пришлось увеличить массу втрое с длинной стороны, а не с короткой (в точности как со штангой на рис. 6.4). Иначе говоря, нужно применить втрое большую силу с короткой стороны, чем с длинной.

В конечном итоге силы, которые следует приложить перпендикулярно доске, чтобы установить равновесие, должны соответствовать: F_A l_A = F_B l_B, где l_A и l_B – расстояние до оси вращения. Другими словами, моменты силы по отношению к оси вращения должны компенсировать друг друга.

Из данного утверждения можно сделать много выводов: наша доска, насаженная на острие, выступает увеличителем силы. В нашем примере силы в 3 ньютона, приложенной к длинной стороне, достаточно, чтобы компенсировать силу в 9 ньютонов, приложенную к короткой (соотношение длин один к трем).

Предположим, что нам нужно поднять массу в 1000 кг: если мы хотим сделать это обычным способом, необходимо применить силу в 1000 ньютонов (F = mg), а это очень тяжело. Но мы также можем поместить эту массу на конец рычага, одно плечо которого в десять раз длиннее другого: сила, приложенная с длинной стороны, будет в 10 раз меньше и составит 100 ньютонов. Такая сила нужна, чтобы поднять 10 кг, а это гораздо легче… В данном случае мы воспользовались большим плечом рычага.

Архимеду приписывают фразу: «Дайте мне точку опоры, и я переверну Землю». С достаточно длинным рычагом можно применить силу такой величины, которая нам требуется.

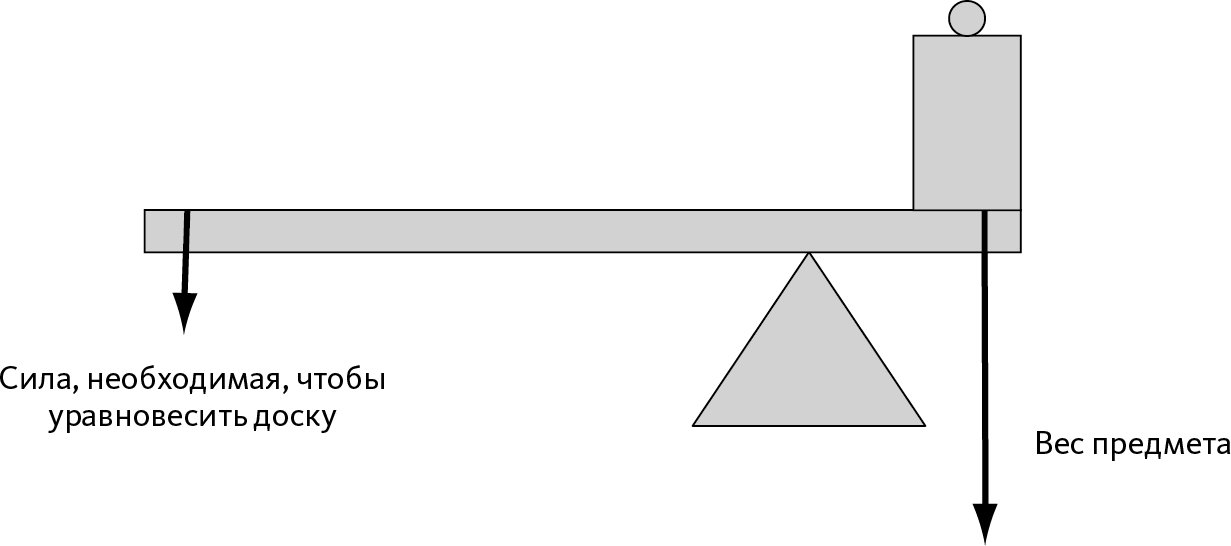
Рис. 6.5 – Эффект рычага