5. Силы инерции
Когда мы находимся внутри машины, которая поворачивает направо или тормозит, наше тело, соответственно, наклоняется влево или вперед. Эти силы, воздействие которых мы ощущаем, не связаны с материальной окружающей средой. Их называют силами инерции, которые включают в себя «переносную силу» и «силу Кориолиса». Мы увидим, что их существование весьма относительно: оно зависит от инерциальной системы отсчета так же, как движение Солнца вокруг Земли, которое по сути лишь видимость. Эти силы также оказывают огромное влияние на жизнь на Земле: в частности, они влияют на ветра и морские течения, которые, в свою очередь, оказывают значительное влияние на климат.
В конце этой главы мы вернемся к гравитации и увидим, что ее существование также зависит от точки зрения наблюдателя: образ Вселенной, где гравитации не существует, более чист концептуально. Это будет поводом сделать первый шаг к парадигме общей теории относительности.
1. Происхождение сил инерции
Псевдосилы
Движение в неинерциальной системе отсчета
Мы рассмотрели почти все силы, которые влияют на нас в повседневной жизни. Можно было бы прибавить силу магнитного поля, не столь очевидную, влияние которой ощущается не часто и природа которой гораздо сложнее. Ее описание мы оставим для главы, где более подробно остановимся на электромагнетизме.
В инерциальной системе отсчета именно совокупность этих сил (и только этих сил) в случае необходимости придает нам ускорение: ma→; = F→;. Таким образом, мы можем понять движение любого объекта, просто наблюдая за его окружением.
Проблема в том, что в некоторых случаях опыт показывает, что наша земная система отсчета, столь важная для нас, не является инерционной: такое происходит, когда мы наблюдаем за движением воздушных масс или океанов. Этому невозможно найти объяснение, если мы примем в расчет только влияние окружающей среды. Это будет равносильно тому, как если мы будем рассматривать движение предмета внутри машины или поезда.
Мы уже давали этому некоторое объяснение с помощью рис. 1.3 и 1.4. Теперь мы рассмотрим все более подробно, чтобы лучше понять природу движения, с которым нам предстоит столкнуться в этих неинерциальных системах отсчета.
Вспомним наш опыт с мячом, лежащим на горизонтальной поверхности в машине. Если машина едет с постоянной скоростью по прямой, мяч будет неподвижен: реакция опоры полностью компенсирует его вес. Общая сила воздействия на мяч, следовательно, равна нулю (объект псевдоизолированный), и, как следствие, ускорение мяча тоже: уравнение ma→; = F→; вполне применимо, так как машина является инерциальной системой отсчета.
Теперь, если машина затормозит, мяч покатится вперед (потому что он стремится сохранить постоянную скорость относительно дороги): это показано на рис. 1.4, который мы воспроизвели ниже (➙ рис. 5.1). На этот раз возникает ускорение по отношению к машине, хотя окружающая среда не изменилась.
Итак, у нас есть выбор между двумя вариантами:
• либо мы считаем, что уравнение ma→; = F→; больше неприменимо и нужно найти другой закон;
• либо мы считаем, что уравнение ma→; = F→; должно всегда удовлетворять определению силы. Это подразумевает, что сила F→; теперь не просто зависит от окружающей среды, поскольку она указывает, что F→; = 0→;, тогда как a→; ≠ 0→;.
Мы будем придерживаться второго варианта, чтобы по возможности не нарушать интуитивного смысла силы: если ускорение мяча направлено вперед, значит, некая сила толкает его вперед.

Рис. 5.1 – Машина в процессе торможения
Ускорение, связанное с ускорением системы отсчета
Из чего рождается эта сила? Ответ прост.
• машина тормозит, ее скорость по отношению к дороге уменьшается;
• мяч сохраняет постоянную скорость по отношению к дороге;
• следовательно, мяч ускоряется по отношению к машине, что хорошо видно на рис. 5.1.
Иначе говоря, ускорение, направленное вперед и действующее на мяч в системе отсчета машины, является результатом «отрицательного ускорения» машины по отношению к дороге.
Теперь рассмотрим случай, когда машина поворачивает влево с постоянной скоростью. Это рис. 1.3, который мы воспроизводим ниже (➙ рис. 5.2)
Мяч катится вправо, то есть на него действует сила, направленная вправо.
Уточним:
• по отношению к дороге машина поворачивает налево;
• мяч стремится сохранить прямолинейную траекторию по отношению к дороге;
• следовательно, мяч катится вправо по отношению к машине, что хорошо видно на рис. 5.2.
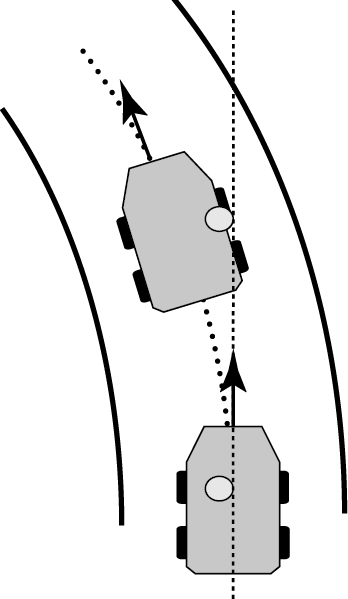
Рис. 5.2 – Машина в процессе поворота налево
Иначе говоря, сила, направленная вправо и действующая на мяч в системе отсчета машины, возникает из-за «ускорения влево» машины по отношению к дороге.
В обоих случаях машина приобретает ускорение в инерциальной системе отсчета (дороге), что вызывает «обратное ускорение» мяча по отношению к машине: если машина ускоряется влево по отношению к дороге, мяч ускоряется вправо по отношению к машине. Если машина «ускоряется назад» (тормозит) по отношению к дороге, мяч «ускоряется вперед» по отношению к машине.
Следовательно, в системе отсчета машины «псевдоизолированный объект», которым является мяч, испытывает ускорение a→;, противоположное ускорению a→;e машины по отношению к инерциальной системе отсчета дороги.
Мы запишем это как a→; = –a→;e. Ускорение a→;e называется «переносным ускорением».
Поскольку мы хотим привести это к уравнению F→; = ma→;, получается, что F→; = –ma→;, это сила, действующая на изначально неподвижный мяч внутри машины. Ее называют силой инерции переноса и обозначают F→;ie.
«Фиктивная» сила?
Мы видим, что эта сила не связана с материальным окружением и отражает лишь некоторую точку зрения (человека в машине). Но мяч только продолжает прямолинейное равномерное движение по отношению к дороге. Человек, стоящий у края дороги, увидит, что мяч просто катится прямо, в то время как машина поворачивает налево.
И нам хочется назвать эту силу фиктивной, кажущейся, которой на самом деле не существует. Однако для человека в машине, который наблюдает странные перемещения мяча, эта сила отнюдь не фиктивна, и мы склонны дать ей название псевдосилы.
В предыдущем примере мы говорили о силе инерции переноса. С помощью других, более общих примеров мы обнаружим другие силы инерции того же происхождения, но с несколько другими последствиями. Их беглый обзор мы сделаем в следующих абзацах.
Запомним: «сила инерции» – это сила, возникающая при движении в неинерциальной системе отсчета по отношению к другой системе отсчета, которая является инерциальной. Она является псевдосилой в том смысле, что не зависит от материальной окружающей среды, а присуща рассматриваемой системе отсчета.
Подведем итог с помощью примера довольно близкого к предыдущим: предположим, что человек бросает мяч вперед со скоростью 1 км/ч в машине, поворачивающей налево со скоростью 50 км/ч.
• С точки зрения человека, стоящего у края дороги, мяч продолжает равномерное прямолинейное движение со скоростью 51 км/ч (➙ рис. 5.3.а).
• С точки зрения человека в машине мяч описывает дугу вправо со скоростью, которая, по крайней мере, вначале равна 1 км/ч (➙ рис. 5.3.b).
Человек у дороги не видит проявления какой-либо силы, но человек в машине «видит» действие силы вполне реальной.
Сила переноса и сила Кориолиса
Если в предыдущем параграфе мы рассмотрели понятие «силы инерции», то пока еще не во всех ее аспектах. Чтобы дать более исчерпывающий ответ, рассмотрим пример, когда ребенок катит мяч, сидя на крутящейся карусели. Если не учитывать силу трения мяча, мы снова имеем дело с «псевдоизолированным» предметом: на него действуют только силы инерции.
Земная система отсчета в данном примере является инерционной, и с точки зрения человека, который сидит рядом с каруселью, мяч движется равномерно и прямолинейно. Но в системе отсчета карусели его движение гораздо более сложное.
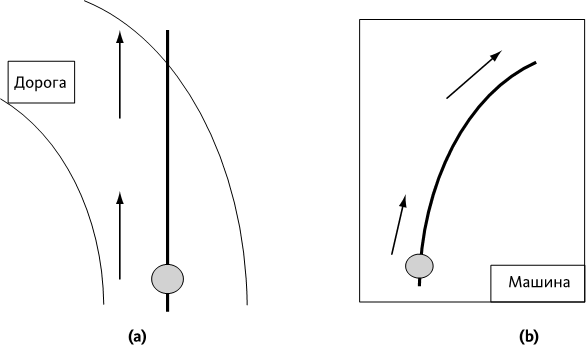
Рис. 5.3 – Траектория мяча с двух разных точек зрения
(а) – траектория с точки зрения человека, стоящего у края дороги (она соответствует пунктирной прямой на рис. 5.2).
(b) – траектория с точки зрения человека в машине (видно, что мяч приближается к правой стенке машины на рис. 5.2).
Центробежная сила
Предположим, что ребенок просто положил мяч на пол карусели. Что произойдет с мячом?
С точки зрения человека рядом с каруселью шарик с самого начала обладает скоростью благодаря вращению карусели. Между тем с его точки зрения мяч будет стремиться продолжать движение прямо, в то время как под ним вращается карусель, то есть мяч в конечном итоге упадет с карусели, как можно видеть на рис. 5.4.а.
С точки зрения ребенка на карусели мяч, сначала неподвижный, катится к краю карусели, потому что в итоге он с нее упадет (➙ рис. 5.4.b): есть ускорение, направленное к краю, что объясняет существование силы инерции в системе отсчета карусели. Речь идет центробежной силе, которая выталкивает каждый предмет за пределы вращающейся системы отсчета.
Именно эту силу мы и описывали в примере с машиной, где мяч катился вправо, когда машина поворачивала налево. Здесь сила также направлена к краю поворота: именно она прижимает пассажиров к правой дверце.
Центробежная сила является частью того, что мы называем силой переноса.
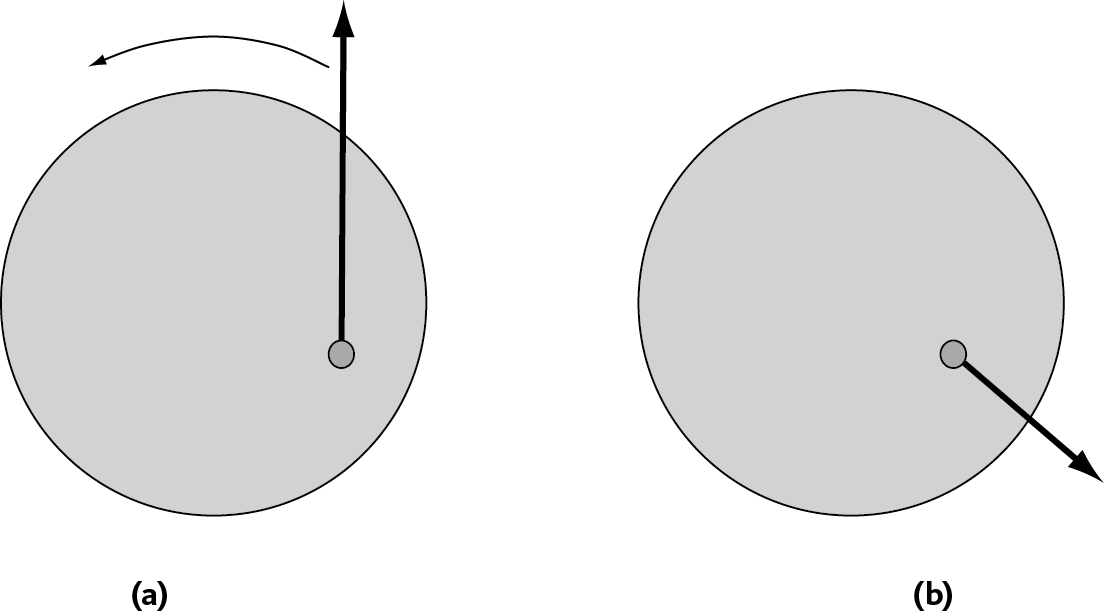
Рис. 5.4 – Происхождение силы Кориолиса
(а) – точка зрения взрослого, сидящего возле крутящейся карусели: он видит мяч, который катится прямо, как и положено.
(b) – точка зрения ребенка на карусели (которая кажется ему неподвижной): он видит, что мяч катится к краю, что видно и на схеме (а).
Необходимо учесть, что мяч изначально неподвижен на схеме (b), а на (а) у него есть скорость благодаря вращению карусели.
Другая составляющая силы переноса
Предположим опять, что шарик изначально неподвижен по отношению к карусели, но карусель на этот раз ускоряет свое вращение.
Поскольку карусель вращается, мяч покатится к краю. Но карусель вращается все быстрее и набирает скорость по отношению к земной поверхности, а мяч стремится сохранить по отношению к земле ту же скорость. Получается, что мяч катится медленнее карусели и начинает катиться к задней части карусели, поскольку сила инерции направлена назад.
Таким образом, здесь одновременно действуют две силы: одна направлена к краю (центробежная), другая назад. Именно совокупность этих двух воздействий называют переносной силой при вращательном движении системы отсчета.
Сила Кориолиса
Нам остается рассмотреть силу, которую мы до сих пор оставляли в стороне. Вернемся к карусели, которая вращается с постоянной скоростью против часовой стрелки: мяч, изначально неподвижный, покатится с ускорением к краю карусели. Предположим, что радиус карусели 4 м и она вращается со скоростью 10 км/ч. Мы положили мяч в 2 м от центра (то есть посередине между центром и краем): с точки зрения человека возле карусели мяч изначально движется со скоростью 5 км/ч.
Предыдущие выводы указывают, что мяч движется к краю карусели; но по отношению к земной поверхности мяч вовсе не стремится набрать или снизить скорость и движется по-прежнему со скоростью 5 км/ч. Однако он подкатывается к краю карусели, которая вращается со скоростью 10 км/ч: то есть мяч движется медленнее и по отношению к карусели начинает отклоняться от первоначальной траектории (➙ рис. 5.5). С точки зрения человека на карусели мяч, двигаясь к краю, смещается вправо (➙ рис. 5.6). На него действует новая сила инерции, которая называется силой Кориолиса.
Также если мы толкнем мяч к центру карусели, он покатится от зоны более высоких скоростей к зоне более низких: то есть мяч будет катиться быстрее, чем вращается карусель, и его траектория снова отклонится вправо.
В сущности, сила Кориолиса всегда будет заставлять мяч отклоняться вправо на карусели, вращающейся против часовой стрелки (а если по часовой стрелке, то влево).
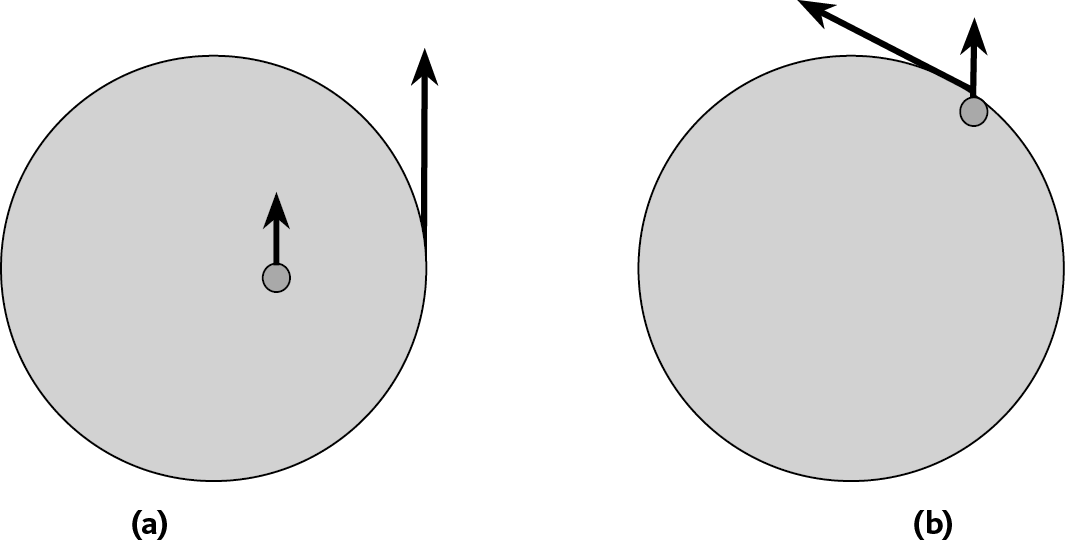
Рис. 5.5 – Происхождение силы Кориолиса
Схема показывает то, что видит взрослый, сидящий рядом с каруселью, за два последовательных момента времени.
(а) – мяч неподвижен по отношению к карусели, но с точки зрения наблюдателя обладает скоростью благодаря вращению карусели. Эта скорость ниже, чем скорость края карусели.
(b) – мяч достиг края карусели, сохранив ту же скорость. В этой точке скорость вращения карусели гораздо выше скорости мяча, и по отношению к карусели он меняет свою траекторию (продолжая двигаться к краю).
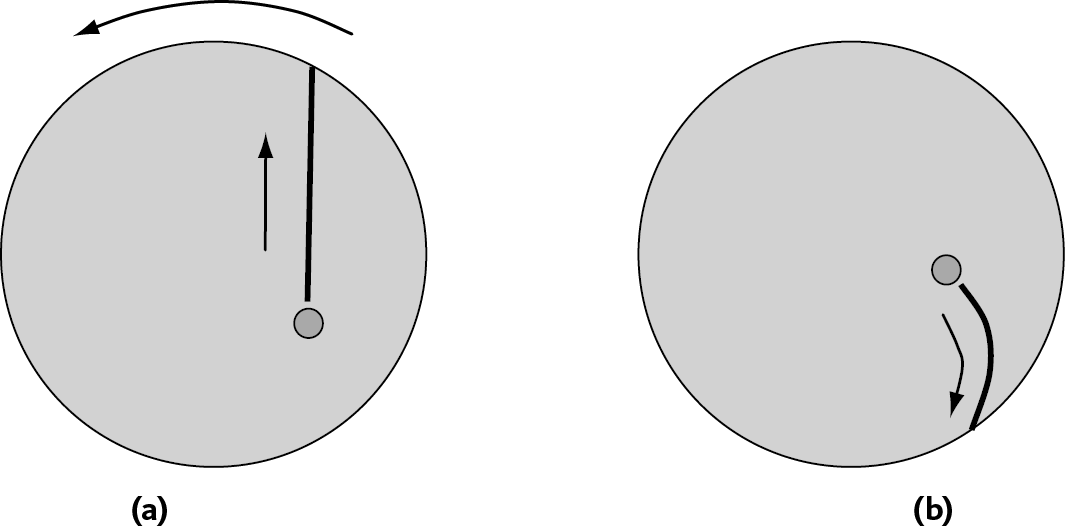
Рис. 5.6 – Траектория мяча, движущегося по карусели, с точки зрения разных наблюдателей
(а) – взгляд человека, сидящего возле карусели: мяч катится по прямой.
(b) – взгляд ребенка на карусели: с одной стороны мяч катится к краю (сила переноса), с другой стороны он описывает дугу вправо (сила Кориолиса).
Обобщение
В конечном итоге если мы различаем «переносную силу» и «силу Кориолиса», то потому, что первая зависит от положения мяча на карусели, а вторая от скорости его передвижения по отношению к карусели.
Наконец, нам пришлось ввести понятие «переносное ускорение» a→;e, связанное с силой переноса F→;ie, как F→;ie = –ma→;e.
Мы также можем ввести понятие «ускорение Кориолиса» a→;c, связанное с силой Кориолиса F→;ik, как F→;ik = –ma→;k.
Подведем итог:
• Ускорение переноса зависит от скорости вращения системы отсчета (в данном случае карусели) по отношению к инерциальной системе отсчета (в данном случае земной поверхности). Она также зависит от изменения скорости вращения и от расстояния объекта до оси вращения (если мяч в центре карусели, он не испытывает никакого ускорения).
• Ускорение Кориолиса также зависит от скорости вращения системы отсчета, но еще и от скорости объекта по отношению к этой вращающейся системе отсчета.
Весьма наглядный пример
Рассмотрим последнюю схему, которая лишь подтвердит положение вещей. Предположим, что ребенок на карусели покатит мяч в сторону противоположную вращению карусели с той же скоростью, с какой вращается карусель. Какова будет траектория мяча?
С точки зрения человека рядом с каруселью важно заметить, что мяч останется неподвижен. И действительно, если в точке мяча карусель вращается со скоростью 10 км/ч, а мяч катится с той же скоростью в противоположном направлении, это значит, что по отношению к земной поверхности он не движется. Это значит, что карусель вращается под мячом, который стоит на месте: когда карусель сделает полный оборот, мяч окажется в первоначальной точке (➙ рис. 5.7). По отношению к карусели мяч опишет ровный круг, который вернет его в исходное место. Ребенок сможет снова взять мяч, который толкнул!
А как это выглядит с точки зрения разных сил? На рис. 5.7 мы видим, что мяч отклонился вправо, чтобы описать круг: это действие силы Кориолиса. Однако сила переноса должна была бы толкнуть его к краю, то есть влево. На самом деле так и происходит, и это значит, что в данном примере сила Кориолиса преобладает над переносной силой.
Чтобы завершить эту часть, уточним, что, если предмет не является псевдоизолированным, достаточно просто добавить силы материальной окружающей среды, а также силы инерции, чтобы определить его движение в неинерциальной системе отсчета.
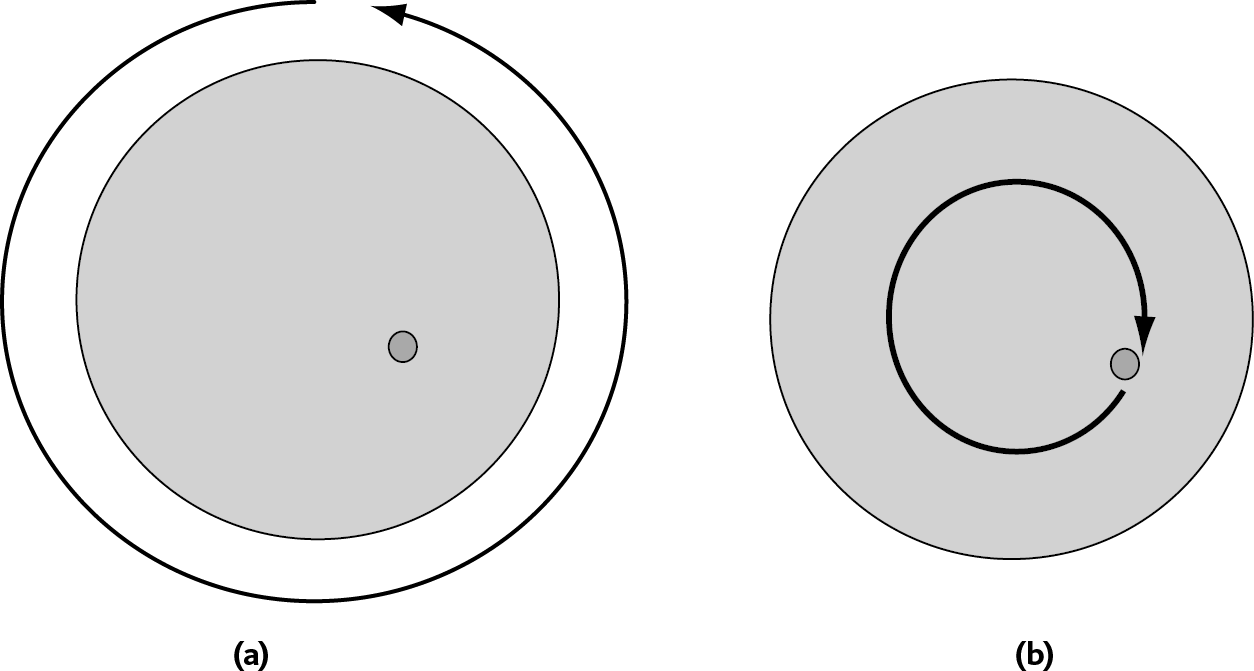
Рис. 5.7 – Мяч, брошенный в сторону противоположную вращению карусели, с точки зрения разных наблюдателей
(а) – точка зрения взрослого рядом с каруселью: мяч неподвижен, карусель вращается под ним, пока не сделает полный оборот.
(b) – точка зрения ребенка на карусели: карусель кажется неподвижной, а мяч описывает ровный круг, прежде чем вернуться на то же место.

