8.1. Мультипликаторы, базирующиеся на текущих ценах акций и будущих финансовых показателях

Мне хотелось бы начать эту главу с такого вопроса: прибыль за какой период времени вы будете использовать при оценке компании по Р/Е? Первый ответ, который прямо напрашивается: «Прибыль за последний финансовый год». И этот ответ — правильный, поскольку прибыль за последний финансовый год, с одной стороны, уже известна, а с другой — это наиболее свежие данные по сравнению с другими годами. Но почему бы не использовать прибыль за последние 12 месяцев, т.е. так называемую скользящую (trailing) годовую прибыль? Или предположим, что мы с вами разговариваем 10 декабря, в то время как финансовый год заканчивается 31 декабря, а результаты компании за 11 месяцев текущего года уже известны. В этом случае мы можем составить довольно точный прогноз результатов года, и если такие же данные доступны и по группе аналогов, то и оценить компанию по ожидаемым результатам текущего года. Следуя данной логике, если мы способны дать достаточно обоснованный прогноз результатов оцениваемой компании и ее аналогов на будущий год и даже на два года вперед, то для чего же нам тогда оценивать компанию на основе ее прошлых результатов, ведь цена акций — это оценка их будущего потенциала, а не прошлого? Вполне логичный вопрос. И вполне закономерно появление мультипликаторов, которые позволяют оценить компанию на основе ее будущих показателей. Это будут те же P/E, Р/S и другие известные нам мультипликаторы, только в знаменателе будут стоять ожидаемые прибыль и выручка текущего года, следующего года, следующих 12 месяцев с момента оценки и т.д. Самый длинный горизонт, с которым я сталкивалась в своей практике, — три года.

С другой стороны, предположим, вы оцениваете компанию из цикличной отрасли. Допустим для простоты, что у отрасли трехлетний цикл. Таким образом, для оценки по историческим показателям можно взять средний показатель прибыли за последние три года. Такая корректировка называется нормализацией. То же самое касается и будущих показателей: можно воспользоваться ожидаемой средней прибылью за будущие три года.

Итак, мы в общих чертах рассмотрели первую разновидность мультипликаторов, строящихся на прогнозах. Это те же самые мультипликаторы, представляющие собой дроби, о которых мы говорили ранее, где в числителе стоят текущие цены акций, а в знаменателе — финансовые или натуральные показатели будущих периодов, то есть показатели общего вида Pt/E(t+n).

Контрольный вопрос 11

Мы с вами уже обсудили многие аспекты работы с мультипликаторами, так что вы сможете легко сформулировать, каковы достоинства и недостатки такого подхода по сравнению с традиционной оценкой на основе исторических результатов. Отложите книгу и задумайтесь, ибо ответ последует тотчас же.

Как я уже неоднократно повторяла, оценка на основе исторических или текущих показателей учитывает разницу в будущих темпах роста сравниваемых компаний. А что же не учитывает оценка на основе прогнозов, отстоящих от момента оценки на пять лет? Ровно обратное: разницу в динамике развития компаний за эти пять лет до даты, на которую рассчитывается мультипликатор. Как правило, при оценке по мультипликаторам аналогами служат компании, акции которых оценены рынком, т.е. котируются, а это обычно компании относительно зрелые. Акции молодых компаний котировок обычно не имеют. Когда нам потребуется подобрать группу аналогов для оценки молодой компании, то, вполне вероятно, мы столкнемся с проблемой, связанной с тем, что все компании в нашей выборке окажутся более зрелыми. А это означает, что они будут иметь более низкие темпы роста в ближайшем будущем.

Проиллюстрируем эту проблему на примере двух компаний, из которых компания Б — оцениваемая, а компания А — аналог. Пусть оцениваемая компания будет совсем молодой, а аналог — более зрелой компанией. Допустим, что на момент оценки величина чистого денежного потока у той и другой компании равна $1. Темпы роста компании А составляют 5% в год вплоть до бесконечности, а компания Б — быстрорастущая. В первые пять лет темпы ее роста составят 20% в год, а затем ее рост стабилизируется и составит 5%, как и у компании Б. Предположим, что рынок оценивает компанию А по дисконтированным денежным потокам и полагает, что норма дисконта для данной компании равна 20%. В этом случае ее рыночная стоимость составляет $6,67. Тогда для компании А показатель Р/FCF1 = 6,67, а Р/FCF6 = 5,22 (при FCF6 = 1,28). Теперь рассчитаем стоимость компании Б по дисконтированным денежным потокам и по полученным нами мультипликаторам. При оценке по дисконтированному чистому денежному потоку при норме дисконта 20% ее стоимость составит $9,86. Применив мультипликатор Р/FCF1, получим оценку в $5,56. Как видим, использование этого мультипликатора оказалось неудачным, поскольку он недооценивает компанию примерно в два раза.

Таким образом, любой мультипликатор, построенный на сегодняшних результатах, дает существенное искажение, если оцениваемая компания и аналог в будущем станут расти разными темпами.

В данном примере эти темпы составляют 5 и 20% в течение 5 лет. Чтобы этого избежать, применим мультипликатор Р/FCF6. В результате наша оценка составит $13,0.

Применение «мультипликатора будущего» дало оценку, которая гораздо ближе к оценке по дисконтированным потокам, однако стоимость компании на этот раз оказалась завышенной. Вспомните, что мы говорили в предисловии относительно ослабления влияния на оценку результатов компании в удаленные годы. Да, применив показатель Р/FCF6, мы приняли во внимание, что в ближайшие пять лет компания будет развиваться быстрее, чем компания А, и грамотно учли в оценке ее конечную стоимость. Но при этом проигнорировали тот факт, что в предыдущие годы динамика чистых денежных потоков у компании А была гораздо хуже.

Оценка по мультипликатору Р/FCF6 означает, что если чистый денежный поток компании Б в шестом году будет в 1,95 раза выше, чем у аналога, то и стоить она должна в 1,95 раза больше. При этом забывается, что в первом году чистый денежный поток был таким же, во втором — выше всего на 14%, и т.п. Применение мультипликатора Р/FCF6 было бы корректным, если бы не существовало разрыва в темпах роста в первые годы.

Как мы видим из приведенного примера, применение «мультипликатора будущего», несмотря на этот недостаток, все же оправданно, поскольку точность оценки возросла. Для быстрорастущих компаний желательно проводить оценку, используя мультипликатор на тот год, когда закончилась фаза быстрого роста, тогда удастся избежать недооценки конечной стоимости компании.

С другой стороны, при построении таких мультипликаторов считается допустимым «заглядывать в будущее» максимум на 2–3 года. В нашем примере это правило оказалось нарушено. Оценка на основе мультипликатора, рассчитанного как отношение сегодняшней цены акций и прибыли через пять лет, может быть существенно искажена.

Несомненным достоинством показателя Pt/E(t + n) является то, что он позволяет устранить одно из основных уязвимых мест показателя Pt/Et, а именно — бессмысленность его расчета в случае отрицательной величины текущей прибыли. Если в знаменателе стоит будущая прибыль, то можно выбрать тот год, когда компания станет прибыльной, если, конечно, убытки — это временное явление.

Еще один аргумент против использования «мультипликаторов будущего» — достоверность прогнозов. Искажение, которое дает неточный прогноз, может перевесить все плюсы от использования мультипликатора. Кроме того, для большинства крупных публичных компаний существует множество разных прогнозов, и если финансовый аналитик работает не в крупном инвестиционном банке, в котором делают собственные прогнозы по большинству акций, то возникнет вопрос, на какие из доступных прогнозов можно полагаться.

8.2. Мультипликаторы с использованием темпов роста

Второй разновидностью мультипликаторов, учитывающих разницу в будущих темпах роста, являются показатели вида (P/Е)/g, или PEG, где Е — текущая прибыль. Темпы роста чистой прибыли g, или G, используемые для расчета этих мультипликаторов, представляют собой средние темпы роста с учетом сложных процентов за прогнозный период. Чтобы подчеркнуть, что это среднегеометрические темпы роста, в англоязычной литературе используют аббревиатуру CAGR (compounded average growth rate — средние темпы роста с учетом сложных процентов).

Мультипликаторы вида (P/Е)/g стали широко применять в период интернет-бума, хотя подобные расчеты проводились и раньше. Их «внедрение» обосновывали тем, что интернет-компании коренным образом отличаются от компаний традиционной экономики по двум параметрам. Не претендуя на научную точность, можно сказать, что этот мультипликатор показывает, по какому P/E можно купить 1% роста.

Во-первых, предполагалось, что интернет-компании будут очень быстро расти. Поясним, что это значит. Для компании традиционной экономики в условиях умеренной инфляции быстрым считается рост около 15% в год. Между тем ожидалось, что интернет-компании будут расти на 100% в год и более (рост с нуля, измеряемый в относительном выражении, всегда очень высок).

Во-вторых, тогда считалось, что развитие интернет-компаний, т.е. компаний виртуальной реальности, потребует гораздо меньших капитальных вложений, чем создание реального бизнеса «на земле». И этот рост будто бы сможет финансироваться из текущих денежных потоков компании (на профессиональном сленге — «через отчет о прибылях и убытках») и не потребует привлечения капитала со стороны. По этой причине применение в оценке интернет-компаний традиционных показателей, таких как Р/Е или P/S, является бессмысленным, так как они не отражают ни будущий рост, ни тот факт, что он не требует больших вложений. Иными словами, предполагалось, что и g, и ROE интернет-компаний будут аномально велики.

С одной стороны, мы присутствовали при рождении новой отрасли, которая действительно начала бурно развиваться и демонстрировать трехзначные темпы роста. С другой — ожидания относительно виртуальной экономики оказались сильно преувеличенными, оценки компаний — завышенными, и мыльный пузырь лопнул.

Достоинства и недостатки мультипликаторов вида (Р/Е)/g практически аналогичны достоинствам и недостаткам мультипликаторов вида P/Et + n, где n — удаленность в будущее (в годах) от того года, на который производится оценка. Этот показатель используется для быстрорастущих компаний. Оценка на основе этого мультипликатора позволяет учесть разницу в среднегеометрических темпах роста аналога (gА) и оцениваемой компании (gБ) за прогнозный период.

Давайте сравним, к каким результатам приводит оценка компании с положительными темпами роста по мультипликатору (P/Е)/g и дисконтированным денежным потокам. Если компании А и Б растут стабильными темпами роста (g) до бесконечности, то для расчета дисконтированной чистой прибыли мы можем воспользоваться формулой Гордона (7):

Рассчитав по этой формуле rА для компании-аналога, применим такой же rБ (равный rА) для оцениваемой компании и найдем ее стоимость по формуле Гордона. Затем найдем стоимость оцениваемой компании по мультипликатору, т.е. исходя из предположения о том, что (РА/ЕА)/gА = (РБ/ЕБ)/gБ:

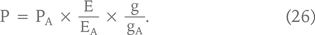
Уже на уровне чистой математики можно заметить, что результаты расчетов по формуле (26) только случайно могут совпадать с результатами дисконтирования. Например, согласно формуле Гордона денежный поток в размере $1, растущий темпами 5% в год и дисконтируемый под 20%, дает капитализацию 1/(20% – 5%) = 1/15% = $6,66. Если же темпы роста денежного потока возрастают в два раза (с 5 до 10%), дисконтирование под 20% приводит к капитализации 1/(20% – 10%) = 1/10 = $10, что в 1,5, а не в 2 раза (как это предполагается при применении показателя (P/Е)/g) выше, чем стоимость потока, растущего на 5% в год.

Из вышеприведенного примера можно видеть, что показатель (Р/Е)/g завышает стоимость акций оцениваемой компании, если аналог растет более медленными темпами. Еще большее искажение в оценке стоимости при использовании (Р/Е)/g возникнет, если оцениваемая компания будет расти более высокими темпами только ограниченный период времени, а затем ее темпы роста снизятся.

Однако не будем списывать этот мультипликатор со счетов. Во-первых, он прижился. Например, финансовый портал Yahoo!, где можно найти обширную информацию по любой котируемой компании, включил его в стандартное описание наряду с P/S и P/E, а других мультипликаторов там нет. Кроме того, как я показываю в разделе «Абсолютное и относительное» главы 12, сходный с ним мультипликатор (DIV/P+g)/(P/E) используется выдающимися инвесторами для грубой прикидки переоцененности или недооцененности акций.

Контрольный вопрос 12

При прочих равных условиях у какой компании показатель (P/Е)/g будет выше?

A. У компании с более высокими или более низкими темпами роста.

Б. У высоко- или низкорисковой компании.

B. У компании с большей или меньшей доходностью акционерного капитала.

Г. У компании, которая реинвестирует большую или меньшую долю прибыли.

8.3. Мультипликаторы, базирующиеся на будущих ценах акций

До сих пор мы конструировали мультипликаторы, основанные на будущих показателях компании, оперируя лишь знаменателем мультипликатора, между тем в числителе стояла текущая цена акций. А теперь я задам очень сложный вопрос, пожалуй, самый сложный в данной книге.

Контрольный вопрос 13

В чем недостатки подхода, при котором по «показателям будущего» мы корректируем только знаменатель мультипликатора? В каких случаях он менее всего применим? Попытайтесь придумать пример.

Такой пример постаралась придумать и я, но о нем речь пойдет чуть позже, а пока мы займемся тем, что введем новый вид мультипликаторов, у которых не только знаменатель, но и числитель являются оценками будущего. Сначала аналитики ввели ожидаемые оценки в числитель мультипликаторов вида «EV/...». Показатель EV, представляющий собой сумму цен акций и чистого долга, стали заменять на сумму вида MC0 + NDt, т.е. на сумму текущей капитализации и будущего чистого долга. Такая сумма является чисто умозрительной конструкцией, однако поправка на будущий долг позволила сделать более корректным сравнение компаний, у которых изменение чистого долга в прогнозном периоде будет демонстрировать разную динамику.

Затем появились мультипликаторы, в числителе которых использовались и будущие цены акций, поэтому мы будем называть их «мультипликаторами на основе форвардных цен» (forward priced, или forward looking multiples). Числитель таких мультипликаторов имеет вид: MCt + NDt.

Мы можем рассчитать цену акции в будущем периоде по следующей формуле:

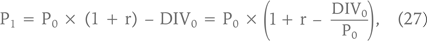
где r — как всегда, доходность, требуемая инвесторами на вложения в данную акцию, DIV — дивиденды, а DIV0/P0 — «доходность акции по дивидендам», или «дивидендная доходность» (dividend yield). Если r1 = r2 = ... = rn и DIV0/P0 = DIV1/P1 = ... = DIVn/Pn; то

Аналогичным образом можно рассчитать и будущую стои­мость компании — EV. Существуют два метода расчета будущей величины EV. Первый метод — прямой: по той же формуле, по которой рассчитывалась будущая стоимость акции. Отличие состоит в том, что при определении стоимости бизнеса (EV) доходность, требуемая инвесторами на вложения в акции, будет заменена в этой формуле на WACC — средневзвешенную стоимость капитала или средневзвешенную доходность для всех сторон, финансирующих компанию, а дивиденды, или денежные потоки акционеров, будут заменены на доходы всех провайдеров капитала, т.е. на свободный денежный поток, попавший в распоряжение акционеров и кредиторов (назовем его в нижеследующей формуле для краткости FCF (денежный поток акционеров и кредиторов — free cash flow)).

Тогда мы получим «аналог» формулы (27) для стоимости бизнеса:

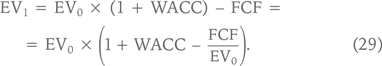
По аналогии с тем, как DIVt/Pt – 1 называют dividend yield, FCFt/EVt – 1 называют FCF yield, что можно попытаться перевести весьма громоздкой фразой «доходность бизнеса по денежному потоку (акционеров и кредиторов)».

Для случая, когда WACC = const и FCF yield = const, формула EVn выглядит следующим образом:

EVn = EV0 × (1 + WACC) – FCF yieldn. (30)

Напомним, что WACC рассчитывается по формуле:

где E — рыночная стоимость акционерного капитала;

re — требуемая доходность на акционерный капитал;

D — рыночная стоимость долга;

rd — процентная ставка по долгу;

t — ставка налога на прибыль;

rd × (1 – t) — посленалоговая (after tax) процентная ставка.

Второй метод — косвенный: тот же результат можно получить, прибавив к будущей рыночной капитализации будущий чистый долг, который, в свою очередь, будет рассчитываться из текущего чистого долга с учетом его изменений (выплаты процентов и изменения основной суммы долга) за требуемый период.

Рассмотрим такие расчеты на примере. Предположим, что текущая рыночная капитализация компании составляет $120, чистый долг — $80, стоимость привлечения акционерного капитала — 12%, а посленалоговая процентная ставка по кредитам — 6%. В году 1 свободный денежный поток компании составит $26, дивиденды — $10, а весь излишек за вычетом процентов и дивидендов пойдет на уменьшение основной суммы долга. В году 2 свободный денежный поток составит $10, компания выплатит дивиденды в размере $8, а недостающие средства для выплаты процентов будут финансироваться за счет нового долга. Нужно найти стоимость акций и стоимость бизнеса в году 2.

Сначала разберемся с будущей стоимостью акций. Согласно формуле (27), стоимость акций в году 1 будет равна: P1 = 120 × (1 + 12%) – 10 = $124,4, а в году 2: Р2 = 124,4 × (1 + 12%) – 8 = $131,3. Теперь рассчитаем стоимость бизнеса в году 1. Согласно формуле (31) средневзвешенная стоимость капитала в году 1 равна: WACC1 = 12% × 120/(120 + 80) + 6% × 80/(120 + 80) = 9,6%. Тогда, по формуле (29), т.е. по расчетам прямым методом, стоимость бизнеса в году 1 будет равна: EV1 = (120 + 80) × (1 + 9,6%) – 26 = $193,2.

Процентные выплаты в году 1 составят $80 × 6% = $4,8. Следовательно, чистый долг уменьшится на 26 – 10 – 4,8 = $11,2 и составит $68,8. В соответствии с косвенным методом: EV1 = 124,4 + 68,8 = $193,2, что в точности совпадает с расчетом прямым методом.

Аналогично для года 2: WACC2 = 12% × 124,4/193,2 + 6% × 68,8/193,2 = 9,86%. В году 2 компания выплатит проценты в размере $68,8 × 6% = $4,13. Долг увеличится на 8 + 4,13 – 10 = $2,13 и составит $70,93. Тогда, используя прямой метод, получим: EV2 = 193,2 × (1 + 9,86%) – 10 = $202,24, а косвенный метод: EV2 = 131,3 + 70,93 = $202,23. Таким образом, результаты практически совпали (разница в одну сотую — ошибка окру­г­ления).

Итак, мы научились рассчитывать мультипликаторы на основе форвардных цен, но в чем смысл этой трудоемкой работы? Как вы догадались, далее будет дан ответ на контрольный вопрос 13. Если посмотреть внимательно на суть мультипликаторов, в которых корректировке на будущие изменения подвергается лишь знаменатель (прибыль, выручка и т.п.), о них шла речь в предыдущих параграфах, то они позволяют учитывать разницу в темпах роста между оцениваемой компанией и аналогом, однако игнорируют источник этого роста. Таким образом, они не учитывают, каким является рост: экстенсивным, т.е. вызванным более высокой долей свободного денежного потока, которая направлена на реинвестирование, или интенсивным — вызванным более высокой доходностью вложений, измеряемой как ROIC (return on invested capital) или ROE (return on equity). Как мы помним, темпы роста компании и доходность капитала связаны простой формулой (20): g = ROE × b, где b — доля реинвестированной прибыли. В табл. 8 показана зависимость темпов роста прибыли от темпов реинвестирования для разной доходности акционерного капитала. Например, при доходности 10% в год и реинвестировании 25% чистой прибыли темпы роста чистой прибыли составят 3%, а при реинвестировании 75% — около 8%.

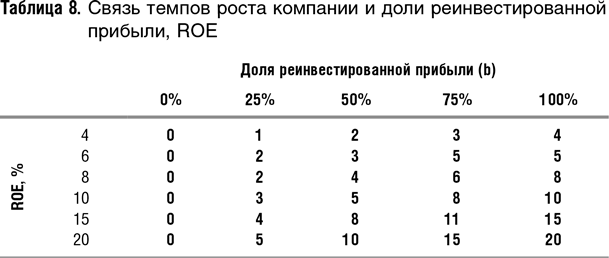
Допустим, что в начальный период времени компании А и Б идентичны практически по всем параметрам, в том числе зарабатывают одинаковую прибыль, за исключением того, что компания А, начиная с этого момента, будет ежегодно выплачивать 80% свободного денежного потока в виде дивидендов, а компания Б будет выплачивать только 20%, а все остальное будет инвестировать в развитие бизнеса. Разу­меется, в этих условиях компания Б станет расти гораздо быстрее. Если мы используем компанию Б в качестве аналога для оценки акций компании А и воспользуемся, например, показателем Р0/Е5 компании Б, где Е5 — прибыль через пять лет, то существенно занизим стоимость акций компании А в настоящий момент. Действительно, прибыль компании А через пять лет будет невелика относительно прибыли компании Б. Но мы не учтем тот факт, что инвестор, вложивший средства в компанию А, все пять лет получал более высокие дивиденды, чем инвестор компании Б. Если у компаний А и Б доходность акционерного капитала одинакова, то и стоить они в настоящий момент должны одинаково. Таким образом, при сравнении компаний с разными темпами реинвестирования прибыли использование мультипликаторов, базирующихся на текущих ценах акций и будущих показателях компании, приведет к существенно искаженным оценкам. Надеемся, что теоретически это понятно, но для большей убедительности рассмотрим пример с теми же компаниями А и Б.

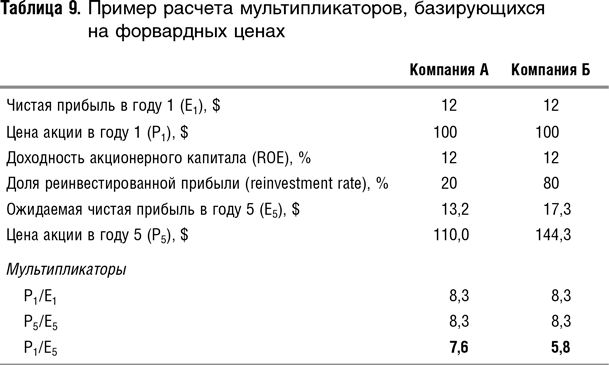
Для простоты представим, что ни одна из компаний не использует заемный капитал. Доходность акционерного капитала (ROE) у обеих компаний составляет 12%, доходность, требуемая акцио­нерами на свои вложения, также равна 12%, а цена акции в году 1 равна $100. В этом году каждая из компаний должна заработать 12% × 100 = $12 чистой прибыли. Согласно (20) у компании А прибыль будет расти темпами 12 × 20% = 2,4%, а у компании Б темпы роста составят 12 × 80% = 9,6%.

Тогда в году 5 компания А заработает только $13,2, в то время как компания Б — $17,3, а при расчете по формуле (27) цены акций составят соответственно $110 и $144,3. Если мы рассчитаем мультипликаторы Р0/Е0 и Р5/Е5 для обеих компаний, то окажется, что P/E на основе текущих цен и прибыли равны, Р/Е на основе будущих цен и будущей прибыли также равны, что является правильным, так как по условию задачи капитализации одинаковых компаний в начальный момент должны быль одинаковыми. Однако мультипликаторы (на основе будущей прибыли и текущей цены акций) не равны, и применение мультипликатора компании Б к оценке компании А занизило бы ее стоимость (см. табл. 9)!

Итак, использование мультипликаторов на основе текущих цен и прогнозируемой прибыли приводит к занижению стоимости компаний с относительно высоким уровнем реинвестирования по сравнению с теми компаниями, которые выплачивают в виде дивидендов бóльшую долю прибыли. К такой же погрешности в оценке привела бы и разница в нормах дисконта для оцениваемой компании и компании-аналога.

Обращаем внимание читателя на то, что при таких расчетах надо быть последовательным в выборе числителя и знаменателя мультипликатора и других показателей. Если мы хотим провести сравнение на основе цены акций Р, т.е. стоимости, приходящейся на долю акционеров, то в знаменателе можно использовать чистую прибыль Е, так как чистая прибыль по своей экономической сути является доходом акционеров. Если же мы будем проводить оценку на основе стоимости бизнеса EV, то в знаменателе может стоять чистая прибыль плюс проценты, иными словами, прибыль с учетом налогов и без учета выплаты процентов (NOPLAT), так как именно эта сумма представляет собой совокупный доход акцио­неров и кредиторов. В первом случае в качестве нормы дисконта мы возьмем доходность, требуемую акционерами на вложения в акционерный капитал оцениваемой компании (r), а в качестве показателя доходности инвестиций (акционеров) — доход на акционерный капитал (ROE). Во втором случае в качестве нормы дисконта мы возьмем средневзвешенную стоимость привлечения капитала (WACC), а в качестве показателя доходности инвестиций — доходность всего инвестированного капитала (ROIC):

Нужно еще раз подчеркнуть, что, умножая прогнозируемую прибыль оцениваемой компании на мультипликатор, рассчитанный на основе форвардных цен акций, мы получаем будущую цену акций или будущую стоимость бизнеса, и для расчета сегодняшней цены акций ее нужно дисконтировать.

Итак, проговорим еще раз всю последовательность шагов, которые нам нужно сделать, чтобы получить цену акций компании Б (оцениваемой) на момент оценки:

• рассчитать будущую цену акций компании А (компании-аналога) на момент времени t с учетом ожидаемых дивидендных выплат;
• используя прогнозируемую прибыль, рассчитать прогнозируемое значение мультипликатора Р/Е компании А на момент времени t;
• применив полученный Р/Е к прогнозируемой прибыли оцениваемой компании, рассчитать стоимость ее акций на момент времени t;
• дисконтируя эту стоимость к настоящему моменту с учетом ожидаемых дивидендных выплат, получить оценку сегодняшней стоимости оцениваемой компании.

Понятно, что в этом случае необходимо знать требуемую доходность на капитал (r), а как говорилось ранее, именно этой проблемы «классические» мультипликаторы призваны избежать. С этой точки зрения мультипликаторы вида P0/Et предпочтительнее: они позволяют находить P0 без дисконтирования.

8.4. Краткие выводы

• Самая простая разновидность мультипликаторов, строящихся на прогнозах, имеет в числителе текущие цены акций, а в знаменателе — финансовые или натуральные показатели будущих периодов, то есть это мультипликатор вида Pt/Et + n.
• Если оценка на основе исторических или текущих показателей не учитывает разницу в будущих темпах роста сравниваемых компаний, то оценка на основе прогнозов, наоборот, не учитывает разницу в динамике развития компаний в будущий период, предшествующий тому году в будущем, на который делается сравнение.
• Любой мультипликатор, построенный на сегодняшних результатах, дает существенное искажение, если оцениваемая компания и аналог в будущем растут разными темпами. Точность оценки может быть повышена за счет применения мультипликатора, строящегося на будущих показателях.
• Для быстрорастущих компаний желательно делать оценку, с одной стороны, используя мультипликатор на тот год, когда закончилась фаза быстрого роста, тогда конечная стоимость компании не будет недооценена; с другой стороны, заглядывать в будущее принято не более чем на 1–3 года, так как более долгосрочные прогнозы менее достоверны.
• Важнейшее преимущество мультипликатора вида Pt/Et + n — возможность оценивать компании, которые на сегодняшний день убыточны.
• Основным недостатком мультипликаторов, базирующихся на будущих результатах, является меньшая достоверность прогноза по сравнению с исторической информацией.
• Второй разновидностью мультипликаторов, учитывающих разницу в будущих темпах роста, являются мультипликаторы вида (P/Е)/g, или PEG, где g (G) — темпы роста чистой прибыли. Они также используются для быстрорастущих компаний. Сравнение на основе этого мультипликатора учитывает разницу в среднегеометрических темпах роста аналога и оцениваемой компании за прогнозный период.
• При высоких темпах роста применение (P/Е)/g дает меньшее отклонение в оценке по сравнению с дисконтированием, чем P/Е.
• Существуют также мультипликаторы, у которых не только знаменатель, но и числитель строятся на основе будущих показателей. При этом числитель может иметь вид: MC0 + NDt (текущая капитализация и будущий долг) и MCt + NDt (будущие капитализация и долг).
• Мультипликаторы, в которых корректировке на будущие изменения подвергается лишь делитель (прибыль, выручка и т.п.), позволяют учитывать разницу в темпах роста между оцениваемой компанией и аналогом, однако игнорируют источник этого роста (тот факт, является ли рост экстенсивным или интенсивным).
• По мультипликаторам, базирующимся на текущих ценах акций и будущих показателях компании, будут получены существенно искаженные оценки, если при этом сравниваются компании с разными темпами реинвестирования прибыли. Использование мультипликаторов, построенных на основе текущих цен и прогнозируемой прибыли, приводит к занижению стоимости компаний с относительно высоким уровнем реинвестирования по сравнению с теми компаниями, которые выплачивают в виде дивидендов бóльшую долю прибыли.