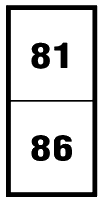
Упражнение «Домино»
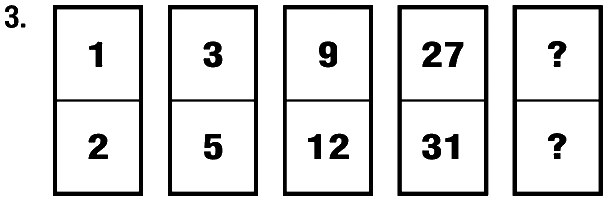
В следующих рядах домино нужно вставить недостающие числа.


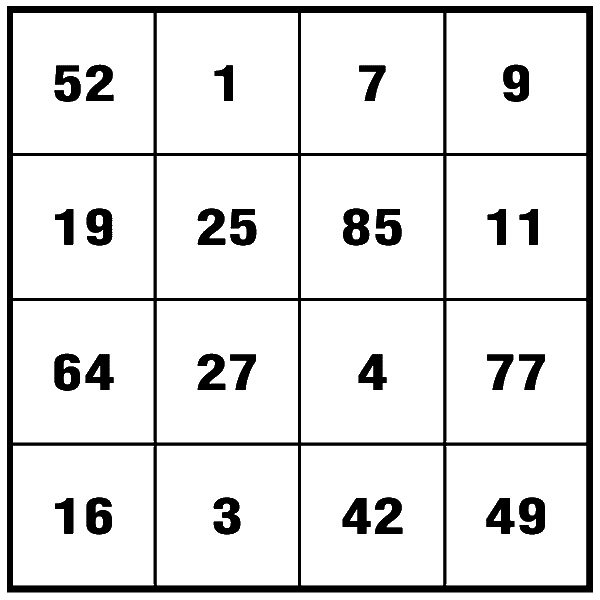
Упражнение «Числа в таблице»
Выполните следующие задания по данной таблице:
1. Перечислите все числа по порядку от наименьшего до наибольшего.
2. Перечислите все нечетные числа по порядку от наименьшего до наибольшего.
3. Перечислите все четные числа по порядку от наименьшего к наибольшему.
4. Назовите все числа, которые делятся только на самих себя и единицу.
5. Назовите все числа, которые делятся только на 11, самих себя и единицу.
6. Назовите все числа кратные двум.
7. Назовите все числа кратные трем.
8. Назовите сумму наименьшего нечетного числа и наибольшего четного числа.
9. Назовите разность наибольшего четного числа и третьего по порядку нечетного числа.
10. Назовите числа, сумма цифр которых составляет 7.
11. Подсчитайте сумму чисел в каждом столбце по вертикали.
12. Подсчитайте сумму чисел в каждой строке по горизонтали.
13. Подсчитайте сумму всех чисел, где есть цифра 2.
14. Перемножьте между собой все однозначные числа.
15. Назовите все числа в обратном порядке – по убывающей, от большего к меньшему.
16. Найдите пары чисел, которые делятся друг на друга без остатка.
17. Найдите числа, из которых можно извлечь квадратный корень.
Ответы
Упражнение 2. Поиск закономерностей
А. 31 (если двигаться против часовой стрелки от меньшего числа, то числа будут возрастать соответственно на 1, 2, 3, 4, 5, 6, 7).
Б. 10 (числа по диагонали в два раза больше или меньше друг друга).
В. 8 (меньшее число нужно умножить на 3 и прибавить 2, чтобы получить число по диагонали).
Г. 12 (числа в верхней половине круга умножаются на два, затем к каждому из них последовательно, двигаясь по часовой стрелке, прибавляется 1, 2, 3, 4).
Д. 16 (большее число по диагонали является квадратом противоположного).
Е. 9 (числа из правой половины круга последовательно, двигаясь по часовой стрелке, делятся соответственно на 3, 4, 5, 6, результаты по диагонали в левой половине круга).
Упражнение 3. Устные вычисления
а) 67;
б) 12;
в) 114;
г) 165;
д) 53;
е) 722;
ж) 180;
з) 48.
Упражнение 4. Числа в квадратах
А. 6 (если двигаться по часовой стрелке начиная от левого верхнего квадрата, то каждое следующее число вдвое больше предыдущего).
Б. 18 (в левом нижнем квадрате отражен результат сложения двух верхних чисел, в правом нижнем квадрате – результат вычитания).
В. 5 (левое верхнее число делится на правое с результатом 3, правое нижнее число делится на 3).
Упражнение 5. Числа в скобках
а) 34 (нужно сложить все цифры обоих чисел за скобками: 9 + 5 + 4 + 3 + 4 + 9 = 34);
б) 27 (из первого числа за скобками вычесть второе);
в) 16 (сложить числа за скобками и разделить на 3);
г) 164 (разность чисел за скобками разделить на 2);
д) 108 (перемножить числа за скобками и разделить на 2);
е) 9 (нужно сложить все цифры числа слева и вычесть результат сложения цифр числа справа: 2 + 6 + 9 = 17, 3 + 1 + 4 + 8, 17 – 8 = 9).
Упражнение 6. Пять задач
Задача 1
1) 360–145 = 215 яблок;
2) 145 – 98 = 47 мелких груш;
3) 215 – 67 = 148 крупных яблок;
4) 98 + 148 = 246 крупных фруктов;
5) 47 + 67 = 114 мелких фруктов.
Задача 2
1) 115 – 30–57 = 28 натюрмортов;
2) 115 – 55 = 60 картин малоизвестных художников;
3) 60: 3 = 20 картин каждого жанра малоизвестных художников;
4) 30–20 = 10 портретов известных художников;
5) 57–20 = 37 пейзажей известных художников;
6) 28–20 = 8 натюрмортов известных художников.
Задача 3
Если двое вскопают весь участок за два часа – 120 минут, значит, работая по одиночке, каждый огородник будет копать в два раза дольше, то есть 240 минут. Если они будут работать втроем, каждому нужно будет вскопать треть участка. Зная, что каждый вскопает весь участок за 240 минут, можем узнать, что треть участка один огородник осилит за 240: 3 = 80 минут. Соответственно, весь участок втроем будет вскопан за 80 минут – 1 час 20 минут.
Задача 4
Пешеход идет со скоростью 6 км/час, то есть проходит 6 км за 60 минут, следовательно, 1 км он проходит за 60: 6 = 10 минут. Значит, 4 км он пройдет за 10 × 4 = 40 минут. Велосипедист за 60 минут может проехать 20 км, следовательно, один километр он проедет за 60: 20 = 3 минуты, а 4 километра за 4 × 3 = 12 минут. Таким образом, велосипедист опередит пешехода на 40–12 = 28 минут.
Задача 5
1) 480 : 3 = 160 – приехало отдыхающих на второй день;
2) 160 × 2 = 320 – приехало отдыхающих на третий день;
3) 480 + 160 + 320 = 960 – всего приехало отдыхающих;
4) 960 : 2 = 480 – отдыхающих разместили в двухместных номерах;
5) 480 : 2 = 240 – потребовалось двухместных номеров;
6) 960 : 4 = 240 – разместили в одноместных номерах (столько потребовалось одноместных номеров);
7) 960 : 4 = 240 – разместили в трехместных номерах;
8) 240 : 3 = 80 – потребовалось трехместных номеров;
9) 240 + 240 + 80 = 560 – всего потребовалось номеров;
10) 620 – 560 = 60 – осталось свободных номеров.
Упражнение 7. Геометрические задачи
1. 40 см (диаметр окружности равен стороне треугольника – 5 см, периметр звезды составлен восемью сторонами треугольников).
2. Стороны прямоугольника должны составлять 2 см и 9 см.
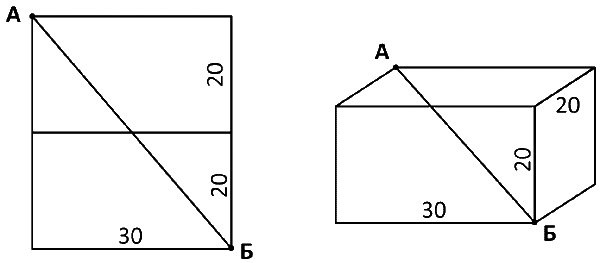
3. Нужно мысленно расположить верхнюю и боковую грани ящика так чтобы они оказались в одной плоскости, тогда станет ясно, что кратчайший путь – диагональ образовавшегося прямоугольника. Эта диагональ является гипотенузой прямоугольного треугольника с длиной катетов 30 см и 20 + 20 = 40 см. Следовательно, подсчитать длину этого пути можно по теореме Пифагора, согласно которой квадрат гипотенузы равен сумме квадратов катетов: 302 + 402 = 900 + 1600 = 2500. Извлекаем корень квадратный из 2500 и получаем длину кратчайшего пути улитки – 50 см.
Упражнение 8. Занимательные задачки
1. Отец старше сына на 26 лет, следовательно, в момент, когда отец оказался в два раза старше сына, отцу было 52, а сыну 26.
2. 53 рубля – чай, 3 рубля – сахар.
3. 662 страницы. (Считаем: чтобы пронумеровать страницы с 1-й по 9-ю, требуется 9 цифр, с 10-й по 99-ю – 180 цифр, далее, с 100-й по 999-ю – 2700 цифр. Следовательно, на нумерацию книги в 1000 страниц требуется 9 + 180 + 2700 = 2889 цифр. Чтобы узнать, сколько страниц в нашей книге недостает до 1000, вычтем 1875 из 2889, получим 1014. Это количество цифр на недостающих до 1000 страницах. Поскольку эти страницы уже явно имеют трехзначные номера, делим полученное число на 3, результат – 338. Затем вычитаем 338 из 1000 и получаем искомый результат: 662).
4. 12 граммов корицы и 6 граммов кардамона (если 4 грамма имбиря – это две части, то одна часть составляет 2 грамма).
5. На расстоянии 140 км (каждому из них предстоит проехать час до встречи, один проедет 60 км, другой – 80).
6. Придется непрерывно считать 11 суток 13 часов 46 минут и 40 секунд – именно в таком отрезке времени содержится ровно 1 000 000 секунд.
7. Два землекопа. (Один землекоп роет по полметра за час, следовательно, за 100 часов каждый из них выкопает по 50 метров, а вдвоем – 100 метров.)
Упражнение 9. Домино
1. По диагонали от числителя к знаменателю и от знаменателя к числителю числа последовательно возрастают на 2, 3, 4 и 5.

2. Числители увеличиваются на 3, 4, 5, 6, а знаменатели увеличиваются на 4, 5, 6, 7.

3. Каждый следующий числитель больше предыдущего в три раза. Каждый знаменатель равен числителю плюс соответственно 1, 2, 3, 4, 5.