Левый дракон – OLL 39

ЛЕВЫЙ ДРАКОН-OLL 39

Левый дракон решается и запоминается аналогично правому, но с левой руки

L – [F¹ (L¹ U¹ L U) F] U¹ – L¹

Вероятность ситуации (Probability) – 1/54.

Чтобы смоделировать ситуацию Левого дракона необходимо на собранной шапке сделать Левый мягкий знак с точкой.

Квадраты

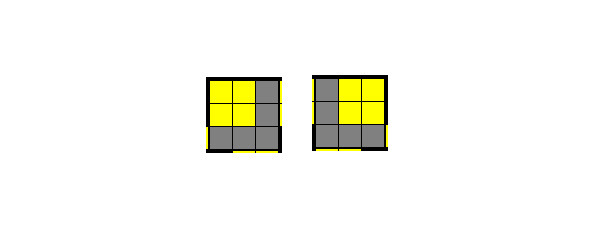
Левый и правый квадраты

Левый и правый квадраты очень похожи, и необходимо научиться различать их. Под каждым большим квадратом есть ухо. Если ухо слева, то и квадрат левый, а если ухо справа, то квадрат – правый.

Так как квадраты симметричны, то алгоритм решения будет один, только для правого квадрата с правой руки, а для левого с левой.

Правый квадрат – OLL 6

ПРАВЫЙ КВАДРАТ-OLL 6

С алгоритмом решения Правого квадрата читатель уже знаком, но в нём есть небольшое изменение.

Для того, чтобы решить Правый квадрат нужно сделать рыбку с ухом (акулу) с первым и последним «жирным» ходом. Алгоритм решения Правого квадрата – OLL 6

Rw U2 R¹ U¹ R U¹ Rw¹

Как видим алгоритм не нужно запоминать, нужно запомнить, что первый и последний ход надо делать двойным («жирный»). Запоминалка: «В квадратную сеть попадаются жирные акулы».

Вероятность ситуации (Probability) – 1/54.

Как смоделировать Правый квадрат?

Есть несколько способов смоделировать Правый квадрат

1) На собранной шапке сделать алгоритм Левой молнии с блоком (правую жирную рыбку Язь – Rw U R¹ U¹ R U2 Rw¹)

2) так как цикл алгоритма Правого квадрата равен 6, то если на собранной шапке 5 раз сделать алгоритм Правого квадрата, то получим ситуацию Правого квадрата

В первом способе работает правило рыбка с глазом и рыбка с ухом моделируют друг друга. Как видим, правило работает и для жирных рыбок

Левый квадрат – OLL 5

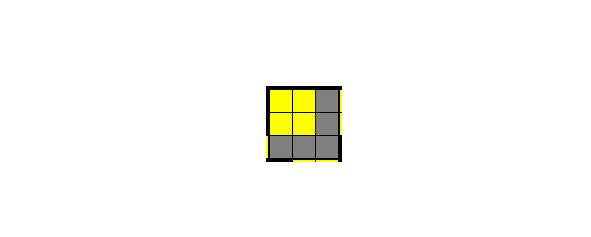
ЛЕВЫЙ КВАДРАТ – OLL 5

Левый квадрат решается аналогично правому, только с левой руки.

Алгоритм решения Левого квадрата (OLL 5)

Lw¹ U2 L U L¹ U Lw

Вероятность ситуации (Probability) – 1/54.

Как смоделировать ситуацию:

1) На собранной шапке сделать алгоритм Правой молнии с блоком (левую жирную рыбку Язь – Lw¹ U¹ L U¹ L¹ U2 Lw)

2) так как цикл алгоритма Левого квадрата равен 6, то если на собранной шапке 5 раз сделать алгоритм Левого квадрата, то получим ситуацию Левого квадрата.

Буквы М

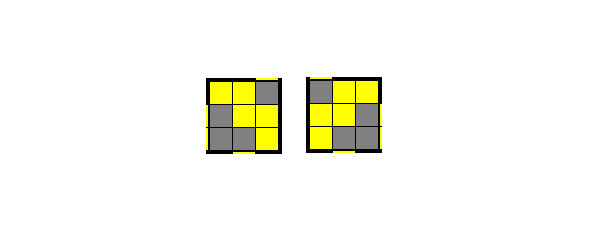
Левая и Правая буква М

Левая и правая буква М отличаются по расположению двойного блока. Если двойной блок слева, то это Левая буква М. Если двойной блок справа, то видим Правую букву М.

Правая буква М – OLL 38

ПРАВАЯ БУКВА М – OLL 38

Алгоритмом решения Правой буквы М (OLL 38) будет

(R U R¹ U) (R U¹ R¹ U¹) (R¹ F R F¹)

Если посмотреть на алгоритм и разбить его на пиф-пафы, то увидим, что идёт последовательность трёх пиф-пафов: «рыбного», «мясного» и «кувалды». Запоминалка для буквы М (левой и правой): «В магазине Метро открылись отделы – рыбный, мясной и отдел кувалд».

Вероятность ситуации (Probability) – 1/54.

Так как цикл буквы М равен 5, чтобы смоделировать Правую букву М надо на собранной шапке сделать 5 раз алгоритм правой буквы М.

Левая буква М – OLL 36

ЛЕВАЯ БУКВА М-OLL 36

Алгоритм решения Левой буквы М (OLL 36)

(L¹ U¹ L U¹) (L¹ U L U) (L F¹ L¹ F)

Вероятность ситуации (Probability) – 1/54.

Так как цикл буквы М равен 5, чтобы смоделировать Левую букву М надо на собранной шапке сделать 5 раз алгоритм Левой буквы М (или прокрутить формулу задом наперёд, но мне нужно чтобы алгоритм запомнился как можно лучше).

Векторы

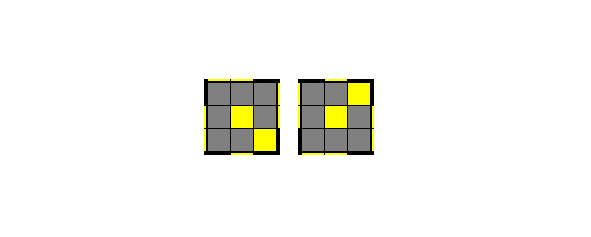
Вектор «вниз» и вектор «вверх»

Чтобы различать векторы, надо «направить стрелку» в правую сторону от центра. Хотя для формулы, который я использую это особо неважно-направление вектора повлияет на один ход в формуле. Как его делать и так понятно будет

Вектор «вниз» – OLL 03

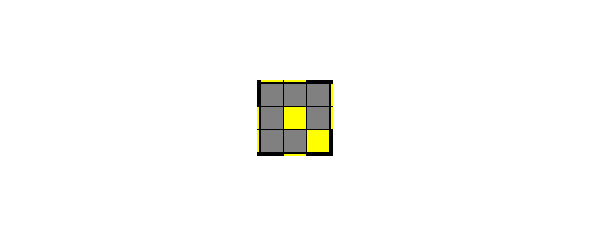
ВЕКТОР «ВНИЗ» – OLL 03

Алгоритм решения ситуации Вектор «вниз» (OLL 03)

[Fw (R U R¹ U¹) Fw¹] U¹ [F (R U R¹ U¹) F¹]

Как видно из формулы первая часть от правого мягкого знака, далее появившуюся букву Т ставим в правильное для решения (ход U¹) и применяем алгоритм для решения худой тётки

Вероятность ситуации (Probability) – 1/54.

Как смоделировать?

На собранном кубике

сделать алгоритм Вектора «вверх»

три раза сделать алгоритм вектор «вниз» – цикл алгоритма равен четырем.

Вектор «вверх» – OLL 04

ВЕКТОР «ВВЕРХ» – OLL 04

Алгоритм решения Вектора «вверх» (OLL 04)

[Fw (R U R¹ U¹) Fw¹] U [F (R U R¹ U¹) F¹]

Алгоритм отличается одним ходом-этим ходом появившаяся буква Т ставится в правильное положение, запоминать этот ход тоже не нужно.

Вероятность ситуации (Probability) – 1/54.

Как смоделировать?

На собранном кубике сделать алгоритм Вектора «вниз» или

три раза сделать алгоритм вектор «вверх» – цикл алгоритма равен 4.