Облегченный Фридрих. Простой PLL
Итак, в предыдущем разделе мы рассмотрели 2 вида «палок», и все случаи, которые могут возникнуть после сборки креста. Чтобы этап сборки шапки не пропал даром, из-за того, что необходимо менять ребра или углы в собранной шапке, а новички в основном не знают как менять такие элементы и при этом не разрушать «шапку». Например, замена рёбер у новичков происходит через комбинации рыбок (прямых или зеркальных) или другие формулы, но при этом разрушаются углы. Для того, чтобы этого не происходило, необходимо знать как поменять ребра и/или углы не разрушая собранного верха. Об этом и пойдет речь в данной главе. При этом выучить придется всего одну формулу перестановки рёбер, вторая будет «зеркалом», которая переставляет рёбра в противоположном направлении. Вторая формула будет менять углы (3 или 4). Слово «формула» здесь использовано с очень большой натяжкой. Использование данного метода: 1) сначала перестановка углов; 2) потом перестановка углов способно заменить и отодвинуть изучение PLL, необходимость одновременного изучения OLL и PLL. В тоже время использование краткого OLL и простого PLL уже заметно уменьшит время сборки, что будет стимулировать на изучение остальных случаев: «если изучение такого небольшого количества алгоритмов уже даёт, такой эффект, то что будет если изучить весь Фридрих». Вхождение в метод Фридрих будет лёгким и незаметным. Вы уже будете собирать методом Фридрих, просто будете делать это, используя неполный набор формул.
Перестановка рёбер – PLL (U-permutation)
Для применения алгоритмов будем держать кубик так, что собранная шапка сверху, а правильно установленный кубик на левой грани. Тогда возможны два треугольника сторон.
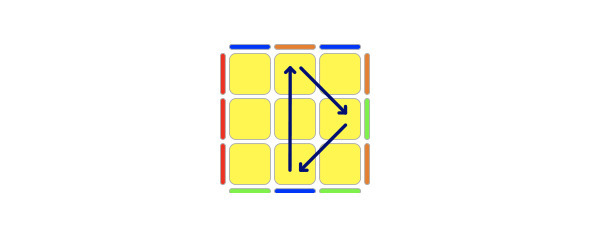
Треугольник сторон ПО часовой стрелке
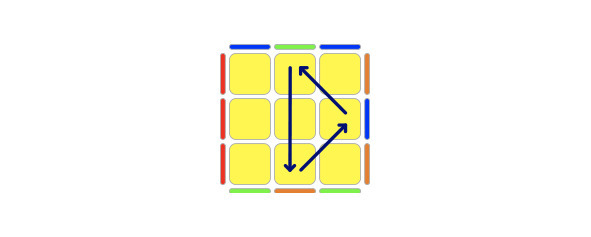
Треугольник сторон ПРОТИВ часовой стрелки
Решением этих двух случаев будут следующие алгоритмы
Треугольник сторон ПО часовой: R2 U S1 U2 S U R2
Треугольник сторон ПРОТИВ часовой: R21 U1 S1 U21 S U1 R21
Как видим, что когда рёбра сторон движутся ПО часовой стрелке, все ходы, кроме S1 и S, делаются ПО часовой стрелке, а когда рёбра движутся ПРОТИВ часовой стрелки все ходы, кроме S1 и S, делаются ПРОТИВ часовой стрелки. На собранном кубике для моделирования ситуации необходимо алгоритм 1 раз. Число цикл треугольников сторон равно 3. Таким образом сделав несколько раз эти формулы они запомнятся механической памятью. Если у нас 2 или 4 кубика не своём месте, то покрутив 1 раз шапку у нас всегда появится один из случаев. Так как двойные повороты можно делать в любую сторону, можно переписать алгоритмы как R2 U S1 U2 S U R2 (рёбра по часовой) и R2 U1 S1 U2 S U1 R2 (рёбра против часовой), которые будут отличаться только одинарным поворотом верхней шапки. Первоначальное написание формулы необходимо для первичного запоминания, чтобы не запутаться. Куда крутить одинарные повороты верха я смотрю по цветам рёбер UF и UR, и кручу в тоже сторону как «ставится» один из них. Аналогичные формулы есть и через средний слой М, а также вообще через движения без средних слоёв. Данные PLL всё равно придется учить, поэтому лучше выучить уже сейчас, когда нам это очень нужно и из-за частого использования запомнится и натренируется очень хорошо.
Перестановка углов
В результате сборки шапки (и при необходимости перестановки рёбер) получаться, что нужно расставить на свои места либо 3 угловых кубика (один кубик на своем месте), либо 4 угловых кубика. Вариант 1
Начнем изучать с простого случая, когда необходимо переставить 3 кубика (один кубик стоит на своём месте)
1) «Правильный» кубик ставим на место B-U-L (задний-верхний-левый).
2) запоминаем цвета кубика F-U-R (передний-верхний-правый). То, что он например, желтый (шапка желтого цвета), можно не запоминать.
3) R1 D2 R;
4) ставим поворотом верхней грани U (ход U или U1) слот с цветами из пункта 2) – то есть, подводим слот, куда должен встать кубик, который запоминали на место F-U-R
5) далее повторяем пункт 2) – 4) еще 2 раза до сборки всего кубика.
В принципе это весь алгоритм, но хотелось бы пояснить пятый пункт. Следующий слот подгоняется ходом U2 (скоро привыкнете сразу подгонять слот таким ходом, далее R1 D2 R-устанавливаем второй угловой кубик. Далее смотрим видим последний слот, в котором нет правильно установленного углового кубика – ходом U или U1, ставим этот слот в положение F-U-R, и комбинацией R1 D2 R-устанавливаем последний угловой кубик одновременно собирая весь кубик.
Вариант 2. Все 4 не на «своих» местах – необходима перестановка 4 кубиков.
1) выбираем «правильным» любой кубик;
2) повторяем пункты 2) – 4) Варианта 1 до появления кубика с цветом нижней грани;
3) Третий кубиком будет кубик с цветом нижней грани. Для такого кубика подогнать любой несобранный слот-выполнить пункт 3) варианта 1;
4) далее выполнять пункты 2) – 5) варианта 1.
Можете прочитать главу Квадрат углов… PLL.
Здесь поясню алгоритм. Сначала вы расставите 2 кубика по своим местам, третий кубик будет с цветом нижней грани (собирали желтую шапку, кубик будет с белой наклейкой) – его ставим в любой «свободный» слот. Появится еще один кубик, который необходимо установить на своё место, у последнего кубика можно не запоминать цвета и подогнав «пустой» слот, установите комбинацией R1 D2 R четвертый кубик.
Если Вы вдруг увлеклись, забыли посмотреть и запомнить цвета углового кубика, то всегда можете подсмотреть цвета этого кубика в месте D-L-B. Но чтобы не запутаться предварительно запомните цвет передней грани, посмотрите цвет незапомненного углового кубика, и сориентировав кубик по цвету (вы его запомнили) передней грани решаете дальше.
Итак, получились следующие этапы сборки кубика
1) первоначальный крест
2) два первых слоя (решаете с F2L или без него, или некоторая смесь)
3) второй крест третьего слоя
4) Базовый OLL
5) PLL рёбер
6) PLL углов
По мере накопления базы OLL вы всё чаще будете пропускать третий пункт. Каждый новый изученный случай OLL будет приближать вас к завершению обучения OLL и переходу к изучению PLL, переходу на полный метод Джессики Фридрих, соответственно уменьшая время сборки кубика. Изучением других случаев OLL и займемся в следующем разделе. Для более легкого запоминания я разобью их на группы.

