Буква L левая с двумя блоками – OLL 14
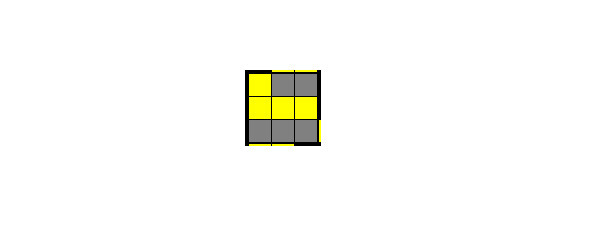
БУКВА L ЛЕВАЯ С ДВУМЯ БЛОКАМИ – OLL 14
Читатель уже наверное сразу догадался, что написание этой главы практически не добавит знаний в копилку. Но написать эту главу диктует структура книги.
Сначала «переворачиваем сковороду».

Сковорода
Алгоритм решения Буквы L с двумя блоками (OLL 14)
(Lw1 U Lw U) (Lw1 U1 Lw) (F U1 F1)
Запоминалка уже наверное не нужна – руки должны помнить алгоритм «правой двойной сковороды».
Вероятность ситуации (Probability) – 1/54.
Как смоделировать ситуацию?
На собранной шапке выполните последовательно 5 раз алгоритм. Цикл формулы равен шести.
Непарные OLL
Раньше уже писал о том, что под понятием «непарные» OLL подразумеваю тот факт, что данные OLL не имеют другого OLL, который решается таким же образом (имеются в виду повороты от центра или к центру) с левой руки. Кстати, многие непарные OLL, потому и не имеют пару, что слишком симметричны (имеют одну или более одной оси симметрии, причём как минимум одна диагональная) или наоборот, слишком асимметричны (не имеют ни одной оси симметрии). Но эти объединяет тот факт, что все OLL при отображении от какой-то оси совпадают сами с собой (возможно с некоторым поворотом). Рисунок парного OLL никаким поворотом в плоскости не преобразуешь в самого себя.
Школа – OLL 57

ШКОЛА – OLL 57
Англоязычной мир спидкуберов называет этот случай как H-OLL. Русские спидкуберы называли буквой Н, пока один из спидкуберов не обратил внимание, что буква Н напоминает школу советского времени, если смотреть на неё с высоты птичьего полета. На пространстве России и бывших советских республик название «Школа» прижилось и закрепилось.
Данный OLL имеет очень даже симметричный и красивый рисунок с несколькими осями симметрии (горизонтальная, вертикальная, диагональные, симметрия от центра). И соответственно рисунок OLL при отображении или некотором повороте преобразуется в самого себя
До некоторых пор для решения Школы (OLL 57) автор использовал алгоритм
L1 (R U R1 U1) L (R1 F R F1)
Запоминал так: «В школе 57 левша включил свет. Выстрелил вверх (пиф-паф). Выключил свет левой рукой и забрал с собой свою кувалду». Но потом он обнаружил («век живи – век учись») другой алгоритм, который мне понравился больше (там всё для правой руки) по нескольким причинам. В этом алгоритме есть ход среднего слоя, но он один и выполняется легко и автор рекомендует выучить его, так как он будет использоваться и для решения другой ситуации и запоминается легче. Алгоритм решения Школы (OLL 57)
(R U R1 U1) M1 (U R U1 Rw1)
Как видим, алгоритм состоит из двух пиф-пафов простого и обратного (анти Пиф-паф) и хода M1 между ними.
Запоминалка: «В школе спидкуберов всё просто. Делаешь букву M1 и Анти-Пиф-Паф с последним жирным ходом».
Вероятность ситуации (Probability) – 1/108.
Как смоделировать?
На собранной шапке сделайте алгоритм Школа (R U R1 U1) M1 (U R U1 Rw1) два раза-получите OLL Школа. Таким образом, цикл алгоритма школа равен трём. Второй вариант моделирования – сделать на собранной шапке один раз алгоритм Стелс – (Rw U R1 U1) M (U R U1 R1).
Стелс. Летающий змей – OLL 28

СТЕЛС. ЛЕТАЮЩИЙ ЗМЕЙ – OLL 28
Данный случай OLL называют Стелс или Летающий змей из-за сходства.
В таком виде как на рисунке Cтелс (OLL 28) решают так
(M1 U M) U2 (M1 U M)
Читатели, которые моделировали Школу заметили, что из собранной шапки алгоритм школа (R U R1 U1) M1 (U R U1 Rw1) сначала моделирует ситуацию Стелс, потом уже Школу.

СТЕЛС. ЛЕТАЮЩИЙ ЗМЕЙ – OLL 28 (повернут)
Из этого следует, что для решения Стелса необходимо выполнить алгоритм Школа наоборот, и тогда соберется шапка.
Алгоритм решения Стелса (летающий змей) – OLL 28
(Rw U R1 U1) M (U R U1 R1)
Вот именно по этой причине эти два OLL Школу и Стелс нужно учить совместно, и никакие запоминалки не понадобятся.
Вероятность ситуации (Probability) – 1/54.
Как смоделировать уже понятно. На собранной шапке сделать алгоритм Школа – (R U R1 U1) M1 (U R U1 Rw1).
Снежинка – OLL 20

СНЕЖИНКА – OLL 20
Это третий и последний OLL (первый – Школа, второй – Стелс), у которого все углы уже на месте.
Данный OLL называют Снежинка. Встречается он довольно редко и поэтому для него я выбрал формулу, которую может не совсем удобно крутить из-за наличия вращений средних слоёв, но запоминается она очень легко.
Алгоритм решения Снежинки (OLL 20)
S R1 U1 – (R U R U R) – U1 R1 S1
В принципе, из-за красоты формулы, её симметричности и легкости моделирования не нужны запоминалки для запоминания формулы. Я её приведу для поддержания структуры книги и для помощи вспоминания на соревнованиях, когда в стрессовых ситуациях спортсмен забывает элементарное. «Я – Снежинка S R1 U1 то R, то U пять раз, потом посмотрела, увидела, что сделала – УПС». Если собираете желтую шапку, то жёлтых кубиков тоже пять – это «последствия».
Другое решение (воскресная фишка от Максима Чечнева)
(M1U1) 3 (M1U) – (M1U1) 3 (M1U)
Как запомнить: (11-11-11-13) 2 раза
Ещё один вариант
MU (R U R1 U1) M2 (U R U1 Rw1)
Данная формула одновременно перемещает ребра против часовой стрелки (переворачивая их) и углы по часовой стрелке.
Вероятность ситуации (Probability) – 1/216.
Как смоделировать ситуацию?
На собранной шапке сделать любой алгоритм Снежинки, и снова Снежинка будет перед нами. Таким образом, у любого алгоритма решения Снежинки цикл равен двум.

