69

69²=4761

1) Данный квадрат можно считать методом близкого квадрата от 70²=4900

69²=4900-70-69=4761

2) методом поиска квадрата по коду

первый код (100—69=31²=961) равен 9, вторые две цифры квадрата 61

код 31—9=22

Первые две цифры квадрата 69—22=47

Итак, 69²=4761

71

71²=5041

7+1+2=5+0+4+1

1) Этот квадрат можно посчитать методом близкого квадрата от 70²=4900

71²=4900+70+71=5041

Методом поиска квадрата по коду

первый код (100—71=29²=841) равен 8, вторые две цифры квадрата 41

код 29—8=21

Первые две цифры квадрата 71—21=50

Итак, 71²=5041.

72

72²=5184

(7+2) *2=5+1+8+4

Методом поиска квадрата по коду

первый код (100—72=28²=784) равен 7, вторые две цифры квадрата 84

код 28—7=21

Первые две цифры квадрата 72—21=51

Итак, 72²=5184.

73 и 77‒третья пара близнецов

73²=5329

77²=5929

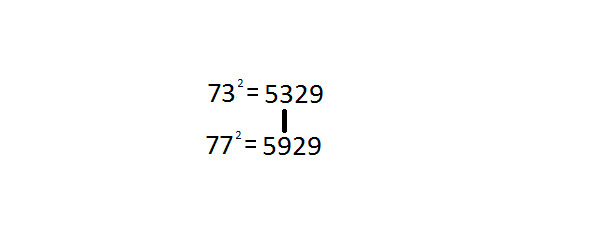
Квадраты 73 и 77

Квадрат 77² запоминается легче так как все помнят, что квадрат 7²=49 и цифра 7 связана с 9, а тут две семерки, значит и девяток должно быть две. также можно заметить что 7=5+2, и расставить между ними девятки.

После этого вспомнить второго близнеца 73 и понять, что меняться может только третья цифра справа (близнецы всегда заканчиваются на одинаковое двузначное число).

Также можно помнить (или вычислить), что у первого близнеца третья цифра, а у второго так как он «далеко» будет третья цифра равна 9=3², самой дальней цифре.

Различные такие аналогии и связи помогают памяти запомнить несмотря на то, что они «притянуты за уши».

74 и 76‒четвертая пара близнецов

Заметим, что числа 24, 26, 74, и 76 как было описано выше рождаются от первого числа 24 как числа последовательности 24, 50±24, 100±24, 150±24 и т. д. и все квадраты этих чисел закончатся на 76. Примечательно, что 100—24=76. Второе такое число, обладающее такими свойствами это 25. Третье число это 99.

Также заметим, что 74 и 76 это четвёртая близнецов (первая пара (24,26), вторая пара (49,51), третья (73, 77)).

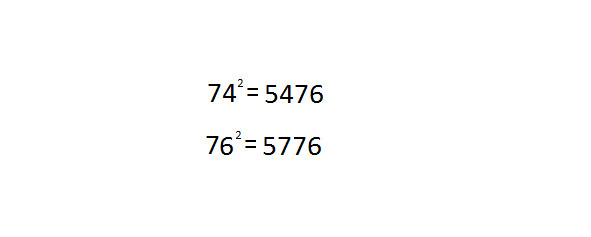
Близнецы 74 и 76

Рассмотрим число 74 и его квадрат.

74²=5476

Для написания этого квадрата используются четыре цифры, которые идут подряд 4, 5, 6, 7. И они записываются таким образом. Сначала пишем зеркальное число от 74 это 47. Потом к числу 47 слева и справа пишем оставшиеся числа в порядке возрастания – это 5 и 6. В результате получится 5476.

Число 76 единственное число имеющее задний код. Этот задний код равен истинному коду и равно числу 19. У остальных чисел от 11 до 99 задний код (возможно само число как-то напоминает о наличии такого кода), если есть, то он не равен истинному коду.

76²=5776

76—19=57

76—19=57 (19 истинный код, который равен заднему)

В этом квадрате зная последние две цифры квадрата 76. А это 76 и вычитая код 19, получим первые две цифры квадрата.

77

По этому числу смотри главу выше 73 И 77‒ТРЕТЬЯ ПАРА БЛИЗНЕЦОВ.

78 расколотый квадрат

Я его так назвал, потому что

78²=6084

Как будто цифра 7 как топор раскалывает цифру 8, она становится 08, и возводится в квадрат 8²=64. Цифры числа 64 становятся по бокам от 08, получается число 6084.

Также можно заметить

78+6+0=84

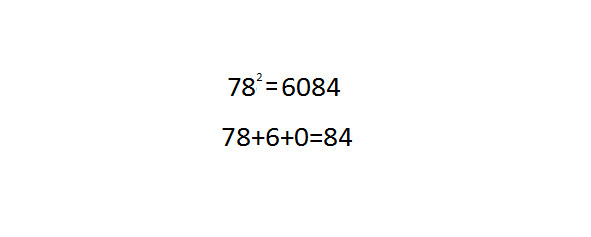
Квадрат 78

Методом поиска квадрата по коду

Первый код (100—78=22²=484) равен 4, вторые две цифры квадрата 84

код 22—4=18

Первые две цифры квадрата 78—18=60.

Итак, 78²=6084.

79

Я его не запоминаю, а считаю назад от квадрата 80²=6400

79²=6400-80-79=6241

У этого числа есть задний код 21=100—79. Задний код легко считается по числу 79 (задний код не равен истинному, но легко запоминается). Вычислив последние цифры квадрата 41, можно прибавив к ним 21 получить первые две цифры квадрата 41+21=62.

81

81²=6561

Можно считать от квадрата 80²=6400

81²=6400+80+81=6561

82

82²=6724

Данный квадрат интересен тем, что

82²=80²+ (100—82) ²=80²+18²=6400+324=6724. Ни у каких других квадратов такого совпадения автор не заметил. Это связано с тем, что совпало (82—50) *200=80².

83‒число-зеркало

Само число 83, как будто цифра 8, состоит из двух 3.

83²=6889

Число 83 может отражаться от зеркала (горизонтали) и переходить в себя и квадрат 6889 может отражаться относительно горизонтали и переходить в себя. Число 6889 необходимо читать сзади и переворачивать одновременно цифры.

Квадрат 83

Очень красивый и запоминающийся квадрат.

84 и 16 дружат с 14

Рассмотрим два квадрата чисел

16²=256

84²=7056

Оба числа (84 и 16) имеют код 14.

Квадрат числа 84 я запоминаю с помощью запоминалки:

«Увидел 84 отними двойной код 14 два раза».

84—14=70 (получаем первую пару квадрата 7056)

70—14=56 (получаем вторую пару квадрата 7056)

86—90 числа на лестнице

Эти числа подробно описаны в главе КВАДРАТЫ ЧИСЕЛ ОТ 86 ДО 90.

88 – золотое число

88²=7744,

Если посмотреть на квадрат числа 88,

Квадрат 88

то увидим красивый повтор цифр. Телефонные номера оканчивающиеся на повторные числа приняты называть золотыми. По аналогии с этим назовем и число 88, и его квадрат золотыми.