Книга: Код. Тайный язык информатики
Назад: Глава 14 Обратная связь и триггеры
Дальше: Глава 16 Сборка памяти
Глава 15
Байты и шестнадцатеричные числа
Две усовершенствованные счетные машины, описанные в предыдущей главе, хорошо иллюстрируют концепцию потоков данных. Восьмибитные значения перемещаются по цепи от одного компонента к другому. Эти значения подаются на входы сумматоров, защелок и селекторов, а также появляются на выходах этих устройств. Кроме того, 8-битные значения задаются с помощью переключателей и отображаются рядом лампочек. Таким образом, поток данных в этих схемах имеет ширину восемь бит. Но почему? Почему не шесть, не семь, не девять и не десять?
Можно было бы ответить, что основой наших усовершенствованных счетных машин является исходный сумматор из главы 12, работающий с 8-битными значениями. Однако нет никаких особых причин конструировать эту машину именно так. Просто при ее создании мы сочли эту величину удобной. Как бы то ни было, признаю, что схитрил, поскольку с самого начала знал (возможно, и вы тоже), что восемь бит данных соответствуют одному байту.
Слово «байт» (byte) возникло в компании IBM примерно в 1956 году. Оно произошло от слова bite («кусок»), но его было решено писать через букву y, чтобы не путать со словом bit («бит»). В течение некоторого времени слово «байт» обозначало просто число битов в конкретном потоке данных. Однако в середине 1960-х, в связи с разработкой семейства компьютеров System/360 в компании IBM, это слово стало обозначать группу из восьми бит.
Как 8-разрядное число, байт может принимать значения в диапазоне от 00000000 до 11111111. Эти значения могут описывать положительные целые числа от 0 до 255, а при использовании дополнения до двойки для представления отрицательных чисел они могут отображать как положительные, так и отрицательные целые числа в диапазоне от −128 до 127. Кроме того, конкретный байт может просто представлять одну из 28, или 256, разных вещей.
Число 8 оказалось весьма удобной величиной. Компания IBM отдала предпочтение 8-битным байтам в связи с простотой хранения чисел в формате BCD (о котором я расскажу в главе 23). Однако, как мы увидим далее, байт идеально подходит для хранения текста, поскольку большую часть языков мира (за исключением идеограмм, использующихся в китайском, японском и корейском) можно представить менее чем 256 символами. Кроме того, байт идеально подходит для представления оттенков серого на черно-белых фотографиях, поскольку человеческий глаз различает примерно 256 оттенков этого цвета. А там, где не хватает одного байта (например, для представления вышеупомянутых идеограмм китайского, японского и корейского языков), как правило, можно использовать два байта, которые позволяют выразить 216, или 65 536, различных элементов.
Половина байта, то есть четыре бита, иногда называется тетрадой, однако это слово употребляется гораздо реже, чем «байт».
Поскольку байты часто используются при описании работы компьютеров, нам требуется как можно более лаконичный способ записи их значения. Например, запись числа, состоящего из восьми двоичных цифр 10110110, безусловно, является корректной, но едва ли лаконичной.
Разумеется, мы всегда можем обращаться к байтам, используя их десятичные эквиваленты, но это потребует преобразования двоичного числа в десятичное, что хоть и несложно, но весьма обременительно. В главе 8 я продемонстрировал один довольно простой подход. Поскольку каждая двоичная цифра соответствует степени 2, мы можем просто записать цифры двоичного числа, а под ними — степени 2, после чего перемножить числа в каждом столбце и сложить результаты. Далее представлен процесс преобразования числа 10110110.
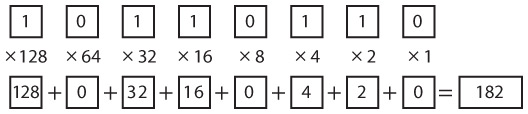
Процесс преобразования десятичного числа в двоичное менее удобен и предполагает деление десятичного числа на убывающие степени двойки. Частное от каждого деления — двоичная цифра, а остаток делится на следующую в порядке убывания степень двойки. Вот как десятичное число 182 преобразуется в двоичное.
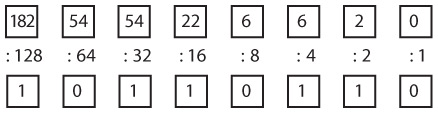
В главе 8 эта техника описана подробно. Тем не менее для преобразования двоичных чисел в десятичные и обратно обычно требуется бумага, карандаш и практика.
Мы уже узнали о восьмеричной системе счисления — системе счисления с основанием 8, где используются только цифры 0, 1, 2, 3, 4, 5, 6 и 7. Преобразовать восьмеричное число в двоичное легко. Все, что нужно, — это запомнить 3-битный эквивалент каждой восьмеричной цифры.
Двоичное число
Восьмеричное число
000
0
001
1
010
2
011
3
100
4
101
5
110
6
111
7
Если у вас есть двоичное число (например, 10110110), начинайте преобразование с правого края. Каждая группа из трех бит соответствует восьмеричной цифре.
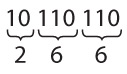
Таким образом, байт 10110110 можно выразить в виде восьмеричного числа 266. Это выражение, безусловно, является более лаконичным, значит, восьмеричная система действительно подходит для представления байтов. Однако у нее есть небольшой недостаток.
В двоичной системе байты выражаются значениями в диапазоне от 00000000 до 11111111, в восьмеричной — значениями в диапазоне от 000 до 377. Как было показано в предыдущем примере, средней и крайней справа восьмеричным цифрам соответствуют группы из трех бит, однако крайней слева восьмеричной цифре соответствуют только два бита. Это означает, что восьмеричное представление 16-разрядного числа не совпадает с восьмеричными представлениями двух байтов, составляющих это 16-разрядное число.
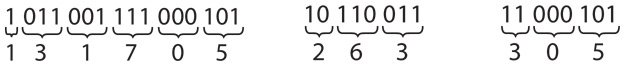
Чтобы согласовать представления многобайтных значений с представлениями отдельных байтов, нужна система, в которой каждый байт делится на равное количество битов. Следовательно, нам требуется разделить каждый байт на четыре значения по два бита каждое (система счисления с основанием 4) или на два значения по четыре бита каждое (система счисления с основанием 16).
Систему счисления с основанием 16 мы еще не рассматривали, и на то есть причины. Система счисления с основанием 16 называется шестнадцатеричной, — даже название труднопроизносимо. В десятичной системе счисления считаем так:
0 1 2 3 4 5 6 7 8 9 10 11 12 …
В восьмеричной системе, как вы помните, не используются цифры 8 и 9:
0 1 2 3 4 5 6 7 10 11 12 …
В системе с основанием 4 не требуются цифры 4, 5, 6 и 7:
0 1 2 3 10 11 12 …
Наконец, в двоичной системе достаточно только 0 и 1:
0 1 10 11 100 …
Однако шестнадцатеричная система отличается тем, что в ней используется больше цифр, чем в десятичной. В шестнадцатеричной системе подсчет происходит примерно так:
0 1 2 3 4 5 6 7 8 9 ? ? ? ? ? ? 10 11 12 …
В данном случае 10 соответствует числу 16ДЕСЯТЬ. Вопросительные знаки говорят о том, что нам нужны еще шесть символов для представления шестнадцатеричных чисел. Что это за символы? Откуда их брать? Что ж, поскольку они не достались нам в наследство, подобно другим традиционным числовым символам, мы можем придумать их самостоятельно, например такие.

В отличие от символов, используемых для обозначения большинства чисел, у этих обозначений есть преимущество: они легко запоминаются и отождествляются с теми величинами, которые представляют. Существует так называемая десятигаллонная ковбойская шляпа, мяч для американского футбола (11 игроков в команде), дюжина пончиков (12 штук), черная кошка (с которой ассоциируется несчастливое число 13), полная луна (появляется на небе через 14 дней после новолуния) и кинжал (напоминающий об убийстве Юлия Цезаря в 15-й день марта). Каждый байт можно выразить в виде двух шестнадцатеричных цифр. Другими словами, шестнадцатеричная цифра эквивалентна четырем битам, или одной тетраде. В следующей таблице показаны соответствия двоичных, шестнадцатеричных и десятичных чисел.
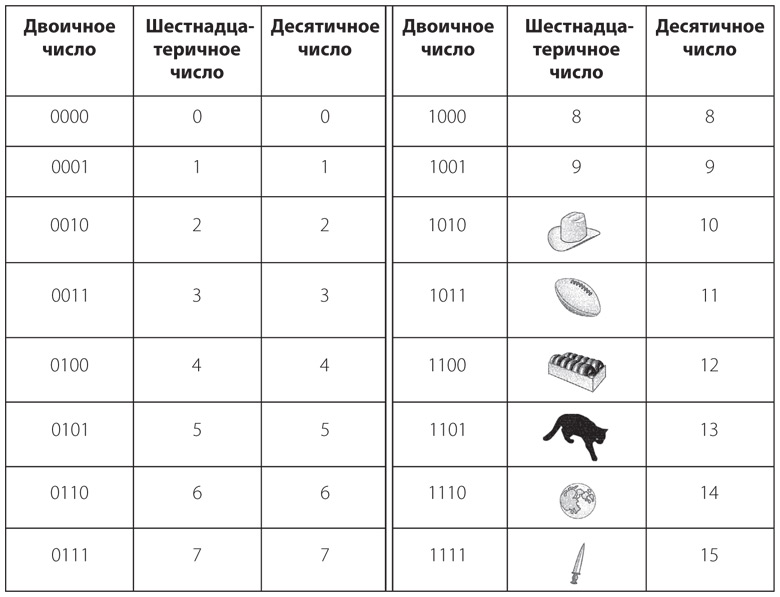
Вот как можно представить двоичное число 10110110 в шестнадцатеричной системе.
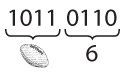
И не важно, имеем ли мы дело с многобайтными числами.
Один байт всегда представляется парой шестнадцатеричных цифр.
К сожалению (а может быть, к счастью), мы не собираемся использовать футбольные мячи и пончики для записи шестнадцатеричных чисел, хотя они, безусловно, могли бы сгодиться для этой цели. Вместо них в шестнадцатеричной системе применяются обозначения, приводящие многих в замешательство. Дело в том, что шесть недостающих шестнадцатеричных цифр представляют шестью первыми буквами латинского алфавита:
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 …
В следующей таблице показано реальное соответствие между двоичными, шестнадцатеричными и десятичными числами.
Двоичное число
Шестнадцатеричное число
Десятичное число
0000
0
0
0001
1
1
0010
2
2
0011
3
3
0100
4
4
0101
5
5
0110
6
6
0111
7
7
1000
8
8
1001
9
9
1010
A
10
1011
B
11
1100
C
12
1101
D
13
1110
E
14
1111
F
15
Таким образом, двоичное число 10110110 можно представить шестнадцатеричным числом B6, не рисуя футбольный мяч. Как вы помните, в предыдущих главах я указывал основание системы счисления с помощью нижнего индекса, например: 10110110ДВА — для двоичной системы; 2312ЧЕТЫРЕ — для четвертичной; 266ВОСЕМЬ — для восьмеричной; 182ДЕСЯТЬ — для десятичной.
По аналогии мы можем использовать обозначение B6ШЕСТНАДЦАТЬ для шестнадцатеричной системы.
Однако такое выражение чересчур громоздко. К счастью, для шестнадцатеричных чисел существуют и другие, более краткие, обозначения. Вы можете записать такое число следующим образом:
B6HEX.
В этой книге я буду использовать распространенный способ представления шестнадцатеричных чисел, предполагающий добавление к числу строчной латинской буквы h:
B6h.
В шестнадцатеричном числе положение каждой цифры соответствует степени числа 16.
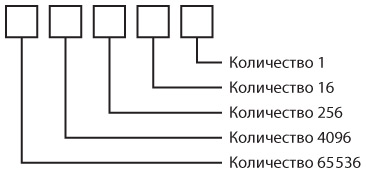
Шестнадцатеричное число 9A48Ch можно представить так:
9A48Ch = 9 × 10000h +
A × 1000h +
4 × 100h +
8 × 10h +
C × 1h.
Это выражение можно записать, используя степени числа 16:
9A48Ch = 9 × 164 +
A × 163 +
4 × 162 +
8 × 161 +
C × 160.
Или десятичные эквиваленты этих степеней:
9A48Ch = 9 × 65 536 +
A × 4096 +
4 × 256 +
8 × 16 +
C × 1.
Обратите внимание на отсутствие двусмысленности при записи отдельных цифр числа (9, А, 4, 8 и C) без нижнего индекса, обозначающего основание системы счисления. Девять — это 9, будь то десятичная или шестнадцатеричная система счисления. С другой стороны, А очевидно представляет шестнадцатеричный эквивалент десятичного числа 10.
По сути, преобразование всех цифр в десятичные числа позволяет выполнить расчет итогового значения:
9A48Ch = 9 × 65 536 +
10 × 4096 +
4 × 256 +
8 × 16 +
12 × 1.
В итоге получается число 631 948. Таким образом шестнадцатеричные числа преобразуются в десятичные.
Шаблон для преобразования любого четырехзначного шестнадцатеричного числа в десятичное выглядит следующим образом.
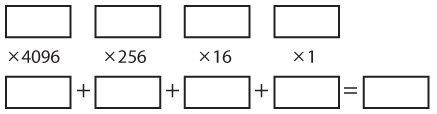
В качестве примера преобразуем число 79ACh. Имейте в виду, что шестнадцатеричные цифры A и C эквивалентны десятичным числам 10 и 12.

Преобразование десятичных чисел в шестнадцатеричные обычно предполагает выполнение операций деления. Число меньшее или равное 255 можно представить одним байтом, состоящим из двух шестнадцатеричных цифр. Чтобы вычислить эти две цифры, нужно разделить число на 16, в результате чего получится частное и остаток. Вернемся к примеру с десятичным числом 182. Разделив 182 на 16, получим 11 (что соответствует цифре B в шестнадцатеричной системе) и 6 в остатке. Так, шестнадцатеричным эквивалентом десятичного числа 182 является B6h. Если десятичное число, которое вы хотите преобразовать, меньше 65 536, то шестнадцатеричный эквивалент будет состоять не более чем из четырех цифр. Шаблон для преобразования такого числа в шестнадцатеричное следующий.
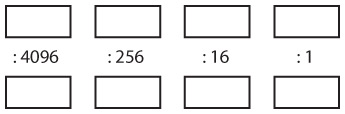
Сначала поместите десятичное число в верхний левый прямоугольник. Это наше первое делимое. Разделим число на 4096 (первый делитель). Частное впишем в прямоугольник, расположенный под делимым, а остаток — в прямоугольник справа от делимого. Этот остаток — новое делимое, которое мы разделим на 256. Вот как число 31 148 преобразуется в шестнадцатеричный формат.
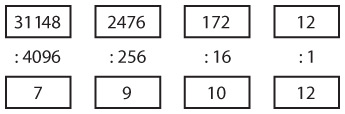
Десятичные числа 10 и 12 соответствуют шестнадцатеричным цифрам A и C, поэтому результат равен 79ACh.
Одна из проблем этой техники заключается в том, что для деления вы, вероятно, решите использовать калькулятор, а калькуляторы не показывают остаток от деления. Если вы разделите 31 148 на 4096 на калькуляторе, то получите 7,6044921875. Чтобы рассчитать остаток, нужно умножить 4096 на 7 (получится 28 672) и вычесть это значение из 31 148. Или умножить 4096 на 0,6044921875 — дробную часть результата от деления. (Правда, некоторые калькуляторы предусматривают функцию преобразования десятичных чисел в шестнадцатеричные и обратно.)
Другой способ преобразования десятичных чисел от 0 до 65 535 в шестнадцатеричные предполагает разделение числа на два байта путем его деления на 256. Затем каждый байт делится на 16. Шаблон для этого следующий.
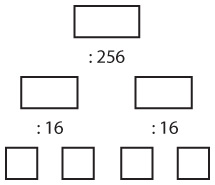
Начнем сверху. После каждой операции деления частное помещается в прямоугольник, расположенный слева от делителя, а остаток — в прямоугольник справа. Например, число 51 966 преобразуется таким образом.
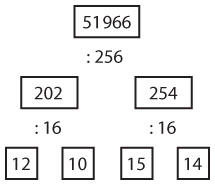
Шестнадцатеричными эквивалентами чисел 12, 10, 15 и 14 являются буквы С, А, F и Е, поэтому результат скорее напоминает слово, чем число.
Далее представлена таблица сложения для шестнадцатеричной системы счисления.
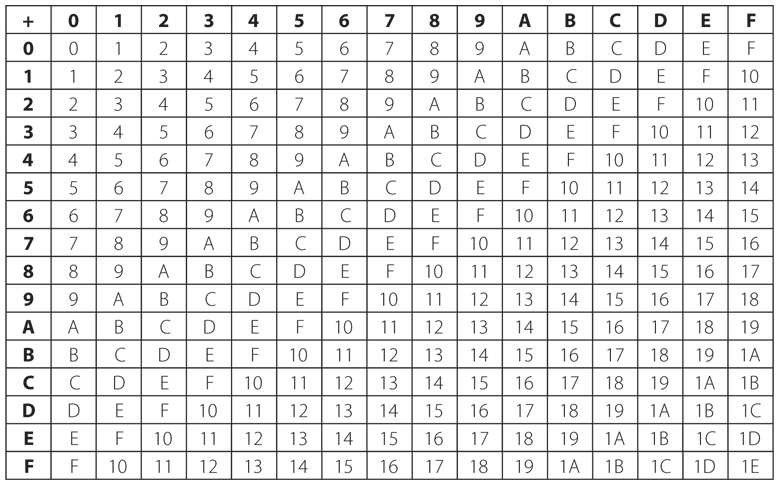
Используя эту таблицу и обычные правила сложения в столбик, можно складывать шестнадцатеричные числа.

В главе 13 я упоминал, что для представления отрицательных чисел можно применять дополнение до двойки. Если вы имеете дело с 8-битными двоичными числами со знаком, то отрицательные числа начинаются с 1. В шестнадцатеричной системе счисления двузначные числа со знаком отрицательные, если они начинаются с цифр 8, 9, A, B, C, D, E или F, поскольку их двоичные эквиваленты начинаются с 1. Например, число 99h может соответствовать либо десятичному числу 153 (если вы знаете, что имеете дело с однобайтными числами без знака), либо десятичному числу –103 (если вы знаете, что это число со знаком).
Кроме того, байт 99h может соответствовать и десятичному числу 99. Это интересно, но, похоже, противоречит всему, о чем мы говорили до сих пор. В главе 23 объясню, как это работает, а теперь остановимся на памяти.
Назад: Глава 14 Обратная связь и триггеры
Дальше: Глава 16 Сборка памяти

