Волны вещества

Как истолковать тот факт, что в спектрах элементов оказываются лишь определенные характерные длины волн?

В физике часто случалось, что существенный успех был достигнут проведением последовательной аналогии между несвязанными по виду явлениями. В этой книге мы часто видели, как идеи, созданные и развитые в одной ветви науки, были впоследствии успешно применены в другой.

Развитие механистических взглядов и теории поля дает много примеров этого рода. Связывание разрешенных проблем с проблемами неразрешенными, внушая новые идеи, может пролить новый свет на наши трудности. Легко найти поверхностную аналогию, которая в действительности ничего не выражает. Но вскрыть некоторые общие существенные черты, скрытые под поверхностью внешних различий, создать на этой базе новую удачную теорию, это важная созидательная работа. Развитие так называемой волновой механики, которое началось с работ де Бройля и Шредингера около пятнадцати лет тому назад, является типичным примером достижений прогрессирующей теории, полученной путем глубоких и удачных аналогий.

Наш исходный пункт – это классический пример, ничего общего не имеющий с современной физикой. Возьмем в руки конец очень длинной гибкой резиновой трубки или пружины и будем двигать его ритмично вверх и вниз так, чтобы конец колебался. Тогда, как мы видели из многих других примеров, колебанием создается волна, распространяющаяся по трубке с определенной скоростью (рис. 72). Если мы представим себе бесконечно длинную трубку, то группы волн, однажды отправленные, будут следовать в своем бесконечном путешествии без интерференции.

Рис. 72.

Возьмем теперь другой пример. Оба конца той же самой трубки закреплены. Если угодно, можно использовать скрипичную струну. Что происходит теперь, когда на одном конце резиновой трубки или струны создается волна? Волна, как и в предыдущем случае, начнет свое путешествие, но она скоро отразится от другого конца трубки. Теперь мы имеем две волны: одну, созданную колебанием, и другую, созданную отражением; они движутся в противоположных направлениях и интерферируют друг с другом. Нетрудно было бы проследить интерференцию обеих волн и определить характер волны, образующейся из их сложения; она называется стоячей волной. Оба слова, «стоячая» и «волна», кажутся противоречащими друг другу; тем не менее их комбинация оправдывается результатом наложения обеих волн.

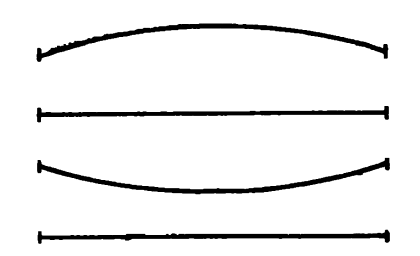
Рис. 73.

Простейшим примером стоячей волны является движение струны с двумя закрепленными концами, вверх и вниз, как показано на рисунке 73. Это движение есть результат того, что одна волна накладывается на другую, когда обе они проходят в различных направлениях. Характерная черта этого движения состоит в том, что в покое остаются только две конечные точки. Они называются узлами. Волна, так сказать, устанавливается между двумя узлами, все точки струны одновременно достигают максимума и минимума своих отклонений.

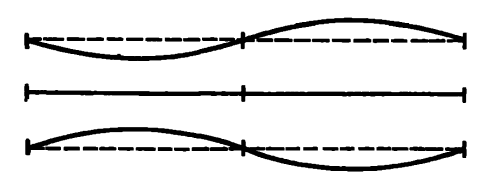
Рис. 74.

Рис. 75.

Но это только простейший вид стоячих волн. Существуют и другие. Например, стоячая волна может иметь и три узла – по одному на каждом конце и один в середине. В этом случае в покое всегда остаются три точки. Из рисунка 74 сразу же видно, что здесь длина волны вдвое меньше длины волны в примере с двумя узлами. Аналогично стоячие волны могут иметь четыре (рис. 75), пять и более узлов. В каждом случае длина волны будет зависеть от числа узлов. Это число может быть только целым и может изменяться только скачками. Предложение вроде «число узлов в стоячей волне равно 3,576» есть чистая бессмыслица. Таким образом, длина волны может изменяться только разрывно (дискретно). Здесь, в этой классической проблеме, мы узнаем знакомые черты квантовой теории. Стоячая волна, созданная скрипачом, фактически еще более сложна, будучи смесью очень многих волн с двумя, тремя, четырьмя, пятью и более узлами, а стало быть, смесью различных длин волн. Физика может разложить такую смесь на простые стоячие волны, из которых она составлена. Или, употребляя нашу прежнюю терминологию, мы можем сказать, что колеблющаяся струна имеет свой спектр, так же как и элемент, испускающий излучение. И так же, как и в случае спектра элемента, здесь разрешены лишь известные длины волн, все же другие запрещены.

Таким образом, мы открыли некоторое подобие между колебанием струны и атомом, испускающим излучение. Странно, как может иметь место эта аналогия, но сделаем дальнейшее заключение из нее и попробуем продолжить сравнение, раз уж мы начали его.

Атом каждого элемента состоит из элементарных частиц: из тяжелых, составляющих ядро, и из легких – электронов. Такая система частиц ведет себя подобно маленькому акустическому инструменту, в котором производятся стоячие волны.

Однако стоячая волна является результатом интерференции двух или более движущихся волн. Если в нашей аналогии есть некоторая доля правды, то распространяющейся волне должна соответствовать еще более простая структура, чем структура атома. Что же имеет наиболее простую структуру? В нашем вещественном мире ничто не может быть более простым, чем электрон, элементарная частица, на которую не действуют никакие силы, т. е. электрон, покоящийся или находящийся в прямолинейном и равномерном движении. Мы могли бы прибавить новое звено в цепи нашей аналогии: движущийся прямолинейно и равномерно электрон – волны определенной длины. Это была новая и смелая идея де Бройля.

Раньше было показано, что имеются как явления, в которых свет обнаруживает свой волновой характер, так и явления, в которых свет обнаруживает свой корпускулярный характер. Уже привыкнув к мысли, что свет есть волна, мы, к своему удивлению, обнаружили, что в некоторых случаях, например в фотоэлектрическом эффекте, свет ведет себя, как ливень фотонов. Для электронов мы имеем теперь как раз обратное положение. Мы приучили себя к мысли, что электроны – это частицы, элементарные кванты электричества и вещества. Были найдены их заряд и масса. Но если в идее де Бройля есть какая-либо правда, то должны быть такие явления, в которых вещество обнаруживает свой волновой характер. Этот вывод, полученный благодаря тому, что мы следовали акустической аналогии, кажется вначале странным и непонятным. Как может движущаяся корпускула иметь что-то общее с волной? Но такого рода трудности мы встречали в физике не раз. Те же проблемы мы встречали и в области световых явлений.

Спектральные линии. (Сфотографировано А. Шенстоном.)

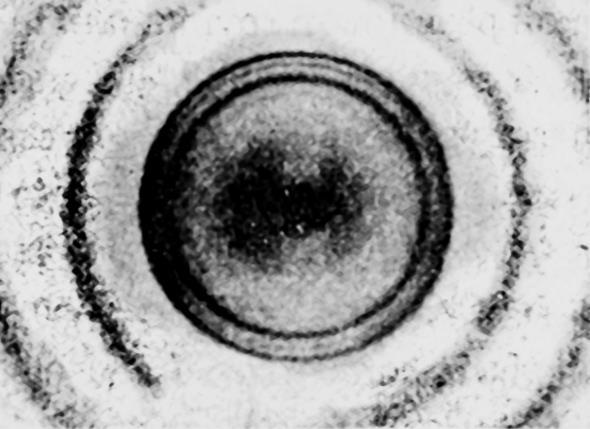
Дифракция рентгеновских лучей. (Сфотографировано Ластовьевским и Грегор.)

Дифракция электронных волн. (Сфотографировано Лориа и Клингер.)

В создании физической теории существенную роль играют фундаментальные идеи. Физические книги полны сложных математических формул. Но началом каждой физической теории являются мысли и идеи, а не формулы. Идеи должны позднее принять математическую форму количественной теории, сделать возможным сравнение с экспериментом. Это можно объяснить на примере той проблемы, с которой мы теперь имеем дело. Главная догадка состоит в том, что равномерно движущийся электрон будет вести себя в некоторых явлениях аналогично волне. Предположим, что электрон или ливень электронов – при условии, что все они имеют одинаковую скорость, – движется равномерно. Масса, заряд и скорость каждого индивидуального электрона известны. Если мы хотим каким-нибудь образом связать понятие волны с равномерно движущимся электроном или электронами, то мы должны поставить следующий вопрос: а что такое длина волны? Это вопрос количественный, и, чтобы получить на него ответ, следует построить более или менее количественную теорию. Правда, это оказалось простым делом. Математическая простота работы де Бройля, дающей ответ на этот вопрос, чрезвычайно удивительна. В то время, когда была написана его работа, математическая техника других физических теорий была относительно очень утонченна и сложна. Математические операции в задаче, касающейся волн вещества, чрезвычайно просты и элементарны, но ее фундаментальные идеи простираются глубоко и далеко.

Раньше, в случае световых волн и фотонов, было показано, что каждое положение, сформулированное на волновом языке, можно перевести на язык фотонов или световых корпускул. То же самое справедливо и для электронных волн. Корпускулярный язык для равномерно движущихся электронов уже известен. Но каждое положение, выраженное корпускулярным языком, можно перевести на волновой язык, как это и было в случае фотонов. Две руководящие идеи привели к формулировке правил перевода. Одна идея – это аналогия между световыми волнами и электронными, или между фотонами и электронами. Мы применяем один и тот же метод перевода как для вещества, так и для света. Другую идею дает специальная теория относительности. Законы природы должны быть инвариантными относительно Лоренцевых преобразований, а не классических. Обе эти идеи приводят к определению длины волны, соответствующей движущемуся электрону. Из теории следует, что электрон, движущийся, скажем, со скоростью 16 000 километров в секунду, имеет длину волны, которую легко можно подсчитать и которая, оказывается, лежит в той же области, что и длина волны рентгеновских лучей. Отсюда мы заключаем далее, что если можно обнаружить волновой характер вещества, то это можно сделать экспериментально таким же путем, каким обнаруживаются волновые свойства рентгеновских лучей.

Вообразим пучок электронов, движущихся равномерно с заданной скоростью, или, если употреблять волновую терминологию, однородную электронную волну и предположим, что она падает на очень тонкий кристалл, играющий роль дифракционной решетки. Расстояния между дифрагирующими элементами в кристалле настолько малы, что они могут создать дифракцию рентгеновских лучей. Можно ожидать аналогичный эффект и для электронных волн, имеющих длину волны того же порядка. Фотографическая пластина должна зарегистрировать эту дифракцию электронных волн, проходящих через тонкий слой кристалла. Эксперимент и в самом деле обнаруживает явление дифракции электронных волн, что, несомненно, является большим достижением теории. Подобие между дифракцией электронных волн и дифракцией рентгеновских лучей особенно заметно из сравнения фотографий (см. фото на стр. 296).

Мы знаем, что такая картина позволяет нам определить длину волны рентгеновских лучей. Это остается в силе и для электронных волн. Дифракционная картина дает длину волны вещества, а полное количественное согласие теории и эксперимента блестяще подтверждает правильность наших рассуждений.

Эти результаты расширили и углубили наши прежние трудности. Это можно уяснить с помощью примера, аналогично примеру, использованному для световой волны. Электронный снаряд при очень малом отверстии будет отклоняться подобно световой волне. На фотографической пластинке обнаруживаются светлые и темные кольца. Есть некоторая надежда объяснить эти явления взаимодействием между электроном и краем отверстия, хотя такое объяснение не кажется очень многообещающим. Но что происходит в случае двух отверстий? Вместо колец появляются полосы. Почему же присутствие второго отверстия полностью изменяет эффект? Электрон неделим и может, казалось бы, пройти лишь через одно из двух отверстий. Как мог электрон, проходя через отверстие, знать, что на некотором расстоянии находится другое отверстие?

Раньше мы спрашивали: что такое свет? Является ли он ливнем корпускул или волной? Теперь мы спрашиваем: что такое вещество, что такое электрон? Частица ли он или волна? Электрон ведет себя подобно частице, когда он движется во внешнем электрическом или магнитном поле. Он ведет себя подобно волне, когда дифрагирует, проходя сквозь кристалл. С элементарным квантом вещества мы прошли через те же трудности, которые мы встретили, изучая кванты света.

Одним из наиболее фундаментальных вопросов, поставленных современными успехами науки, является вопрос о том, как согласовать два противоречивых взгляда на вещество и волну. Это одна из тех фундаментальных трудностей, которые, раз уж они сформулированы, должны привести, хотя и длинным путем, к прогрессу науки. Физика старалась разрешить эту проблему. Будущее покажет, является ли решение, подсказанное современной физикой, окончательным или же временным.