«За» и «против» смешанных стратегий

Из всех тем в теории игр равновесие Нэша в смешанных стратегиях, наверное, вызывает наибольшие разногласия. Сторонники смешанных стратегий подчеркивают, что многие игры, например «Камень, ножницы, бумага» или «Валютная спекуляция», не имеют равновесия Нэша в чистых стратегиях, но в них наблюдается очень интересное равновесие Нэша в смешанных стратегиях. Они также утверждают, что даже в таких играх, как «Кто первый струсит» или «Игра навылет», в которых есть равновесие Нэша в чистых стратегиях, это равновесие зачастую является полностью интуитивным, так как оно выявляет неуверенность игроков.

Тем не менее оппоненты смешанных стратегий заявляют, что случайный выбор не является разумным человеческим поведением. Неужели люди принимают решения наугад? И в связи с тем, что при равновесии участники индифферентны, что мотивирует их выбирать как раз те вероятности, которые подталкивают других игроков к индифферентности?

Одним из защитников смешанных стратегий был американо-венгерский экономист Янош Харсаньи (1920–2000), который ввел понятие «очищение». В 1994 году он разделил Нобелевскую премию по экономике с Джоном Нэшем и немецким экономистом Рейнхардом Зельтеном (род. в 1930 г.).

Янош Харсаньи утверждал, что даже если игроки выбирают чистые стратегии, если присутствует даже малейшее сомнение в выигрышах друг друга, со стороны будет казаться, что они делают случайные выборы.

Знаменитое «очищение» Яноша Харсаньи доказывает, что если игроки почти, но не полностью уверены в выигрышах других участников, то отдельному игроку может показаться, что вероятность выбора другим игроком определенной линии поведения точно равна той вероятности, с которой мы имеем дело в равновесиях Нэша в смешанных стратегиях без неуверенности о чужих выигрышах.

Это значит, что равновесие Нэша в смешанных стратегиях относительно, даже если вы не верите, что людям свойственно принимать решения наугад.

«Уклонение от уплаты налогов»

Одним из примеров равновесия Нэша в смешанных стратегиях являются игроки, которые случайным образом выбирают свои возможные действия. Еще одним примером можно назвать некоторую неуверенность о выигрышах других игроков. Игра под названием «Уклонение от уплаты налогов», в которой взаимодействуют налогоплательщики и налоговая служба, может служить третьим примером.

Представьте ситуацию: женщина, владелица предприятия, должна заполнить налоговую декларацию. Для простоты допустим, что у нее есть два варианта: действовать согласно букве закона или уклоняться от уплаты налогов. Предположим, что с нравственной точки зрения уклонение от уплаты налогов нормально.

Налоговая служба, естественно, может поймать «уклониста», но аудит – это дорогостоящая процедура. Однако в аудите нет нужды, если налогоплательщик не уклоняется от уплаты налогов.

В этой игре нет равновесия Нэша в чистых стратегиях.

Налогоплательщик, несомненно, будет действовать в рамках закона, если точно знает, что его будут проверять. Тут не может быть равновесия Нэша: если налогоплательщик точно будет уплачивать налоги, государству нет нужды проводить аудит.

Налогоплательщик, несомненно, будет избегать уплаты налогов, если уверен, что аудит проводить не будут. Очевидно, что эта ситуация также неравновесна: если налогоплательщик уклоняется, то налоговой службе лучше провести аудит.

Единственное равновесие в этой ситуации – в смешанных стратегиях: налогоплательщики делают случайный выбор между законной деятельностью и уклонением, а налоговая служба наугад выбирает, стоит проводить аудит или нет.

Если в игру «Уклонение от уплаты налогов» играют многие граждане, то значительной альтернативной интерпретацией равновесия Нэша в смешанных стратегиях будет то, что каждый отдельный гражданин выбирает чистую стратегию: он либо «подчиняется закону», либо «уклоняется». Однако равновесие Нэша в смешанных стратегиях формирует вероятность, которая образует часть граждан, выбирающих чистую стратегию «подчиняться закону», и часть граждан, выбирающих чистую стратегию «уклоняться». Налоговому инспектору известно соотношение уклонистов и законопослушных налогоплательщиков, однако он не знает, кто из граждан к какой группе относится.

Повторяющееся взаимодействие

В 1883 году французский экономист Жозеф Луи Франсуа Бертран (1822–1900) изучал ценовую конкуренцию между несколькими фирмами, продававшими одну и ту же продукцию. Те стимулы, с которыми сталкиваются эти фирмы, схожи со стимулами заключенных в «Дилемме заключенных».

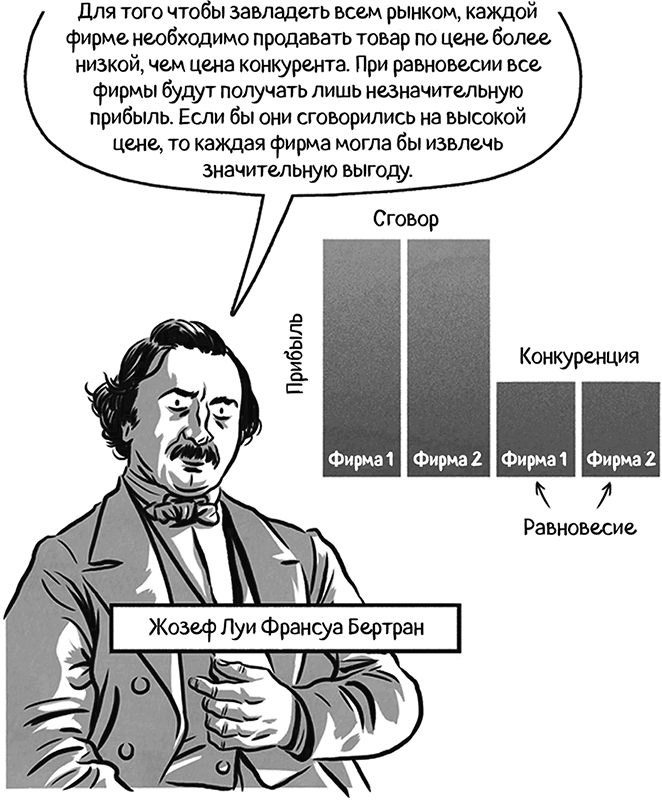
Бертран предсказал, что в равновесии фирмы будут продавать товар по более низкой цене, чем соперник, что похоже на исход {признание, признание} в «Дилемме заключенных». Несмотря на это предсказание, на рынках с небольшим количеством компаний часто можно заметить цены, основанные на сговоре. Большинство западных демократий обладают так называемым «антитрестовским» законодательством для предотвращения подобного сговора (кооперации нескольких фирм) и содействия конкуренции.

Чтобы понять, как игроки сговариваются в ситуациях вроде «Дилеммы заключенных», нам необходимо уйти от однократных игр (в которых участники играют один раз и затем игра кончается) и начать размышлять о более реалистичных сценариях повторяющегося взаимодействия, при котором участники играют в одну игру снова и снова.

Заметили бы мы равновесную кооперацию в «Дилемме заключенных», если бы игроки снова и снова взаимодействовали?

Представьте, что оба игрока знают, что они будут играть в «Дилемму заключенных» не один раз, а два. Чтобы найти равновесие в игре с повторяющимся взаимодействием, нам сначала необходимо предсказать равновесие, которое сформируется в последнем туре. А затем мы размышляли бы о том, каким будет равновесие в первом туре. Такая схема размышления называется обратной индукцией.