Игра «Кто первый струсит»

Равновесие Нэша в смешанных стратегиях может интуитивно казаться более выгодным в ситуациях, когда не существует равновесия Нэша в чистых стратегиях, потому что игроки решают вести себя непредсказуемо. Равновесие Нэша в смешанных стратегиях также интересно исследовать в положениях с множеством равновесий Нэша в чистых стратегиях, при которых каждый игрок предпочитает отличный от чужого равновесный исход.

Классическим примером этого является игра «Кто первый струсит»: два подростка едут в автомобилях навстречу друг другу. Они хотят проверить себя на смелость и определить, кто сможет дольше ехать в прямом направлении. Здесь имеется равновесие Нэша в чистых стратегиях, при котором один подросток продолжает ехать прямо, а другой сворачивает в сторону, а также есть другое равновесие, при котором они меняются ролями. Естественно, для каждого юноши предпочтителен исход, при котором он оказывается смельчаком, а другой – трусом.

Игра «Кто первый струсит» интересна оттого, что, если ни один из водителей не свернет, аварии будет не миновать. Тем не менее авария не является возможным равновесным исходом, если мы рассматриваем лишь равновесие Нэша в чистых стратегиях. Очевидно, если один водитель продолжает ехать по прямой, наилучшим ответом другого будет свернуть в сторону и избежать столкновения.

Чтобы передать увлекательность этой игры, нам необходимо рассмотреть равновесие Нэша в смешанных стратегиях, когда оба игрока наугад выбирают свою линию поведения. В равновесии Нэша в смешанных стратегиях лобовое столкновение – один из возможных исходов.

«Игра навылет»

«Игра навылет» – это пример применения «Кто первый струсит» в экономике. Эта игра наглядно иллюстрирует, как можно найти равновесные вероятности в равновесии Нэша в смешанных стратегиях.

В Смолвилле два продуктовых магазина: Kalemart и Radish. Недавно население этого города сильно уменьшилось. Теперь Смолвилль слишком мал, чтобы оба магазина могли продолжить успешно работать. Тем не менее один магазин сможет вести выгодную торговлю, только если второй закроется. Соответственно, каждый владелец предпочел бы наслаждаться продуктовой монополией в Смолвилле, пока другой покидает рынок.

Эта матрица демонстрирует, какими будут прибыль и убытки Kalemart и Radish при каждом возможном исходе. Если и Kalemart (К), и Radish (R) продолжат работать в городе, то оба магазина понесут убытки (К – 20, R – 50). Эти условные цифры используются для примерной демонстрации более реальных сумм, типа 20 000 фунтов стерлингов и 50 000 фунтов стерлингов. Если оба магазина закроются, то оба не получат никакой прибыли.

Если Kalemart продолжит работать, а Radish закроется, то Kalemart получит выигрыш в размере 80 (К:80), а выигрыш Radish составит 0 (R:0). Если Radish останется в Смолвилле и получит монополию, то он получит выигрыш в размере 100 (R:100), а выигрыш Kalemart будет равен 0 (К:0).

Неудивительно, что компании конфликтуют из-за их положения в Смолвилле, ведь каждая предпочла бы быть единственной в городе. Равновесие Нэша в смешанных стратегиях отражает этот конфликт. Ни один из магазинов не желает сдаваться, точно так же как ни один из подростков не хотел проиграть спор в «Кто первый струсит». И точно так же как в «Кто первый струсит», где любой юноша имел возможность показать свою смелость, в «Игре навылет» каждый магазин продолжает работать с некоторой вероятностью, но без абсолютной уверенности.

Чтобы решить вопрос вероятностей в равновесии Нэша в смешанных стратегиях, необходимо понять, что управление магазина будет принимать случайное решение, только если оно индифферентно к последующей судьбе этого магазина. А индифферентным управление магазина может быть, только если ожидаемая прибыль от работы равна ожидаемой прибыли от прекращения работы.

Если ожидаемая прибыль от одного действия выше, чем от другого, то управление магазина предпочло бы первое действие, и этот выбор был бы сделан с уверенностью. В равновесии случайный выбор и, соответственно, неуверенность в действиях имеют место, только если управление магазина индифферентно, то есть если ожидаемая прибыль от обоих действий равна.

Если Radish «вылетит», его ожидаемая прибыль составит 0 вне зависимости от действий Kalemart:

С другой стороны, если Radish продолжит работать, его ожидаемая прибыль будет зависеть от вероятности того, что Kalemart останется в Смолвилле. Пусть k будет означать вероятность работы Kalemart.

Если k = 0, то нет никакой вероятности, что Kalemart продолжит работу. А если k = ½, то существует 50 %-ная вероятность, что Kalemart будет работать. Если k = 1, то Kalemart точно продолжает работу в Смолвилле. (1 – k) означает вероятность прекращения работы Kalemart.

Если Radish продолжит работать, он понесет убытки, равные –50, при условии, что Kalemart также продолжает работать, что произойдет с вероятностью k. Radish получит 100, если Kalemart «вылетит», что произойдет с вероятностью (1 – k). Таким образом, для Radish:

«Рэдишу» безразлично, продолжать работу или закрываться, только если его ожидаемая прибыль от этих альтернатив равна:

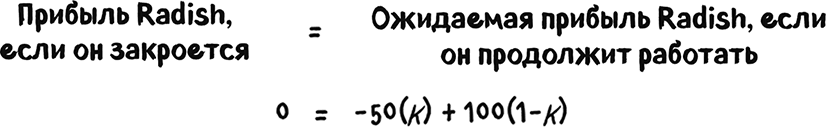
Чтобы найти равновесную вероятность того, что Kalemart продолжит работать, разрешим эту задачу относительно k и получим, что k= ⅔.

Равновесная вероятность того, что Radish продолжит работать, равно ⅘. Это можно рассчитать, пытаясь найти такую вероятность, с которой Kalemart будет безразлично – работать или закрываться.

Если Kalemart продолжает работать, он понесет убытки в размере –20, при условии, что Radish работает, что произойдет с вероятностью ⅘. Kalemart получит прибыль в размере 80, если Radish «вылетит», что произойдет с вероятностью ⅕. Для Kalemart в равновесной ситуации ожидаемая прибыль от прекращения работы (равная нулю) равна ожидаемой прибыли от работы.

В равновесной ситуации Kalemart продолжил бы работу с вероятностью ⅔, а Radish остался бы с вероятностью ⅘, поэтому мы можем рассчитать вероятность каждого возможного исхода.

Вероятность того, что оба магазина закроются, равна 1/15, то есть мы умножаем вероятность того, что Kalemart закроется, на вероятность прекращения работы Radish: (1/3)*(1/5)=1/15.

Вероятность того, что оба магазина продолжат работу, равна 8/15, то есть мы умножаем вероятность того, что Kalemart продолжит работать, на вероятность работы Radish: (2/3)*(4/5)=8/15. В этом случае оба магазина несут убытки. Этот исход похож на один из возможных исходов в «Кто первый струсит», где оба подростка демонстрируют свою смелость и погибают в аварии.

Вероятность того, что Kalemart в конце концов останется единственным магазином в городе, или того, что Radish создаст продуктовую монополию, можно рассчитать этим же способом.

Также возможно смоделировать другую версию «Игры навылет», в которой оба игрока продолжают работать, у них есть возможность закрыть магазин попозже. В этом случае их конфликт продлится еще дольше, а их убытки будут расти. Это явление известно под названием война на истощение. Этот термин был заимствован из военного лексикона. В подобных играх могут происходить затяжные, изматывающие конфликты, даже если выигрыш на самом деле совсем незначителен по сравнению со всеми потерями и убытками.