Книга: Восемь правил эффективности
Назад: Глава 2
Дальше: Часть VII ИННОВАЦИИ Брокеры идей, продуктивное отчаяние и «Холодное сердце»
Глава 3
В конце 1990-х годов профессор когнитивистики из Массачусетского технологического института по имени Джошуа Тененбаум приступил к масштабным исследованиям: ученый хотел знать, каким образом обыкновенные люди делают повседневные прогнозы. Каждый день мы сталкиваемся с десятками вопросов, ответить на которые невозможно без той или иной степени прогнозирования. Допустим, нам нужно прикинуть, как долго продлится собрание, или выбрать маршрут с минимальным количеством пробок, или решить, куда поехать отдыхать всей семьей: на океан или в «Диснейленд». Размышляя о подобном, мы делаем прогнозы, приписывая вероятности различным исходам. Возможно, мы этого не осознаем, но мы мыслим сквозь призму вероятностей. Как наш мозг это делает?
Специальностью Тененбаума была вычислительная когнитивистика – в частности, сходства в процессах обработки информации, свойственных компьютеру и человеку. По сути, компьютер представляет собой детерминированный автомат. Он, конечно, может спрогнозировать, что предпочтет ваша семья (пляж или «Диснейленд»), но только при одном условии: если вы дадите ему четкую формулу для сравнения достоинств пляжных забав и парков развлечений. Человек, напротив, может принять решение даже в том случае, если он никогда раньше не ездил ни на океан, ни в Волшебное Королевство. Основываясь на предыдущем опыте, наш мозг, скорее всего, сделает примерно такой вывод: раз дети вечно ноют «на лоне природы» и обожают смотреть мультфильмы, все получат больше удовольствия от встречи с Микки и Гуфи.
«Каким же образом наш мозг извлекает столь многое из столь малого? – пишет Тененбаум в статье, опубликованной в журнале „Science“ в 2011 году. – Любой родитель знает, и ученые это подтвердили, что типичные двухлетние дети понимают, как правильно употреблять новое слово, например „лошадь“ или „расческа“, увидев всего несколько примеров». Для двухлетнего ребенка лошадь и щетка для волос имеют много общего. На картинках у обеих длинное тело с серией прямых линий, торчащих наружу – в одном случае это ноги, во втором – щетинки. И те, и другие бывают разных цветов. И все же, несмотря на то, что ребенок, возможно, видел только одну фотографию лошади и пользовался только одной расческой, он может быстро понять разницу между этими словами.
Компьютер, напротив, нуждается в подробных инструкциях, когда следует употреблять «лошадь», а когда «расческа». Ему требуется особая программа, в которой будет четко оговорено, что четыре ноги увеличивают шансы на лошадиность, а сто щетинок повышают вероятность расчески. Ребенок производит такие расчеты раньше, чем строит предложения. «С точки зрения оперирования сенсорной информацией это подвиг, – писал Тененбаум. – Как ребенок улавливает границы этих подмножеств, увидев только один или несколько примеров?»
Другими словами, почему мы так хорошо умеем прогнозировать определенные типы событий – и, таким образом, принимать оптимальные решения, – если мы практически ничего не знаем о всех потенциальных обстоятельствах?
Чтобы ответить на этот вопрос, Тененбаум и его коллега Томас Гриффитс провели любопытный эксперимент. Они прочесывали интернет, собирая данные по различным категориям предсказуемых событий, – например, сколько денег соберет фильм в прокате, какова продолжительность жизни среднего человека, сколько времени печется пирог. Интерес к такого рода вопросам объяснялся просто: если для каждого из них построить свой график, то он будет иметь строго определенный вид. Кассовые сборы, например, обычно подчиняются базовому правилу: каждый год выпускают несколько блокбастеров, которые приносят огромную прибыль, и множество фильмов, которые оказываются убыточными.
В математике это называется «степенным распределением». Если доходы от всех кинофильмов, выпущенных в том или ином году, представить на одном графике, то он будет выглядеть так:
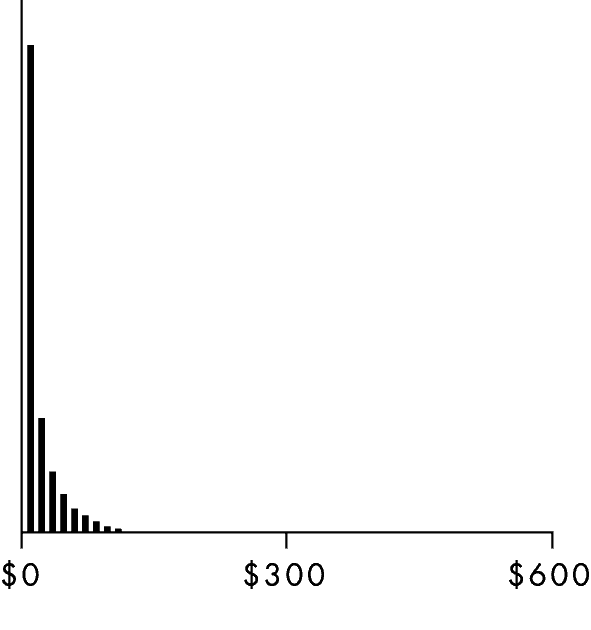
Сборы в прокате
Графики других типов событий выглядят иначе. Возьмем продолжительность жизни. Шансы умереть достаточно высоки в момент рождения – некоторые младенцы погибают, едва появившись на свет, – но если ребенок благополучно прожил первый год, то, скорее всего, он проживет еще несколько десятков лет. После 40 лет шансы умереть начинают повышаться. После 50 лет вероятность смерти резко возрастает с каждым годом, достигая максимума примерно в 82 года. Это и есть средний возраст смерти.
Продолжительность жизни придерживается нормальной, или гауссовой, кривой распределения. График выглядит так:
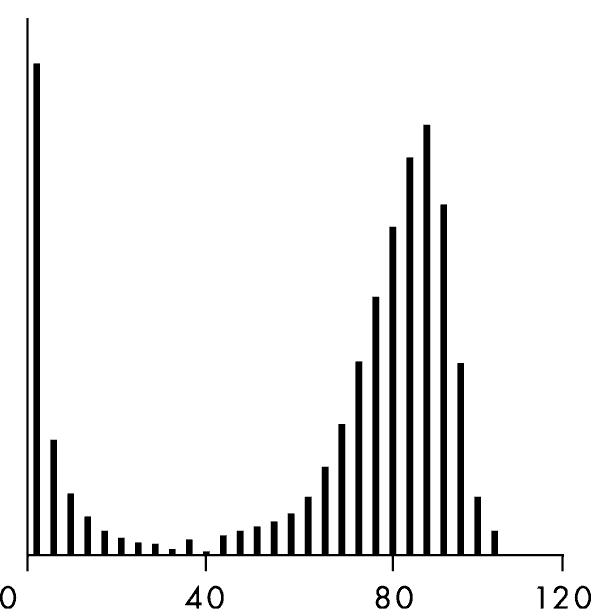
Продолжительность жизни
Большинство людей интуитивно понимают: для прогнозирования различных видов событий нужны разные виды рассуждений. Мы знаем, что кассовые сборы и продолжительность жизни требуют разных типов оценок, даже если нам ничего не известно о медицинской статистике или тенденциях в индустрии развлечений. Тененбаум и Гриффитс хотели выяснить, откуда берутся эти интуитивные знания. Поэтому они выбрали события с четкими закономерностями: от кассовых сборов и продолжительности жизни до средней длины стихотворений, продолжительности карьеры конгрессмена (которая придерживается распределения Эрланга) и времени пребывания пирога в духовке (которое лишено четко выраженных закономерностей).
Затем они попросили сотни студентов предсказать будущее на основании одного фрагмента данных:
Вы читаете о фильме, который собрал на сегодняшний день 60 миллионов долларов. Сколько он соберет в итоге?
Вы встречаете человека, которому 39 лет. Как долго он или она будет жить?
Пирог печется уже 14 минут. Сколько времени он должен оставаться в духовке?
Вы встречаете американца, который является членом конгресса уже 11 лет. Сколько лет он прослужит в конгрессе в общей сложности?
Никакой дополнительной информацией студенты не располагали. Им ничего не рассказали ни о степенном распределении, ни о кривых Эрланга. Их просто попросили сделать прогноз, основанный на одном фрагменте данных без каких-либо подсказок касательно типов вероятностей.
И все же прогнозы участников оказались поразительно точны. Они знали, что фильм, который собрал 60 миллионов, – это блокбастер, который, скорее всего, соберет еще 30 миллионов. Интуиция подсказывала им, что человек, которому стукнул четвертый десяток, вероятно, проживет еще лет 50. Они догадывались, что конгрессмен, который находился у власти в течение 11 лет, наверняка прослужит еще лет шесть или около того: несмотря на то, что длительный срок пребывания в должности дает свои преимущества, даже видные законодатели могут пострадать от новых политических веяний.
В ответ на заданные вопросы лишь немногие из участников сумели описать логику, которой они пользовались при прогнозировании. Они просто давали те ответы, которые казались правильными. В среднем их прогнозы зачастую отличались от правильного ответа менее чем на 10 %. На самом деле, когда Тененбаум и Гриффитс графически представили все предсказания студентов по каждому вопросу, полученные кривые распределения почти идеально соответствовали реальным закономерностям, которые обнаружили профессоры в данных из интернета.
Кроме того, каждый студент интуитивно понимал, что различные виды предсказаний требовали различных видов рассуждений. Это было очень важно. Они понимали – хотя и не обязательно осознавали почему, – что продолжительность жизни имеет форму нормальной кривой, тогда как кассовые сборы, как правило, подчиняются степенному закону.
Некоторые исследователи называют эту способность интуитивно улавливать закономерности «байесовским мышлением» или «байесовской психологией». Дело в том, что для подобных прогнозов компьютер использует ту или иную разновидность правила Байеса – математическую формулу, которая обычно требует анализа тысяч моделей одновременно и сравнения миллионов результатов. В основе правила Байеса лежит следующий принцип: даже при наличии очень малого количества данных прогнозирование будущего возможно. В этом случае нам придется скорректировать наши предположения с учетом наблюдений за окружающим миром. Допустим, ваш брат говорит, что идет ужинать с другом. Поскольку большинство друзей вашего брата мужского пола, вы можете предположить, что он собирается встретиться с мужчиной с вероятностью 60 %. Теперь вообразим, что ваш брат говорит, что этот друг – коллега по работе. В этом случае вы, скорее всего, измените свой прогноз, ибо знаете, что большинство коллег вашего брата женского пола. Правило Байеса позволяет вычислить точную вероятность того, что ваш брат будет ужинать с женщиной или мужчиной, на основании всего одного или двух фрагментов данных и ваших предположений. Чем большим количеством информации вы располагаете – его друга зовут Пэт, он или она любит приключенческие фильмы и модные журналы, – тем точнее вы сможете вычислить вероятности.
Люди делают подобные расчеты, практически не задумываясь, и, как правило, оказываются на удивление точны. Большинство из нас никогда не видели актуарных таблиц продолжительности жизни, но опыт подсказывает нам, что малыши умирают сравнительно редко, а 90-летние старики часто. Большинство из нас не обращают внимание на статистику кассовых сборов, однако мы знаем, что каждый год выпускают несколько фильмов, которые смотрят все, и кучу фильмов, которые исчезают из кинотеатров в течение одной-двух недель. Таким образом, мы делаем предположения о продолжительности жизни и кассовых сборах, основываясь на собственном опыте. Чем больше похорон и кинотеатров мы посетим, тем точнее будут наши догадки. Пусть мы этого и не осознаем, но люди – настоящие асы в байесовском прогнозировании.
Впрочем, иногда и мы совершаем ошибки. Когда Тененбаум и Гриффитс попросили участников предсказать, как долго будет царствовать египетский фараон, если он уже управляет страной 11 лет, большинство студентов сочли, что фараоны ничем не отличаются от других царственных особ – например европейских королей. Из книг по истории и телепередач мы знаем, что некоторые члены королевских семей умирают рано. Однако если король или королева доживает до среднего возраста, то, он или она, как правило, остается на престоле, пока не поседеет. Участникам эксперимента Тененбаума показалось логичным, что у фараонов дела обстоят точно так же. Они предложили ряд догадок, основная масса которых приходилась на 23 года царствования.
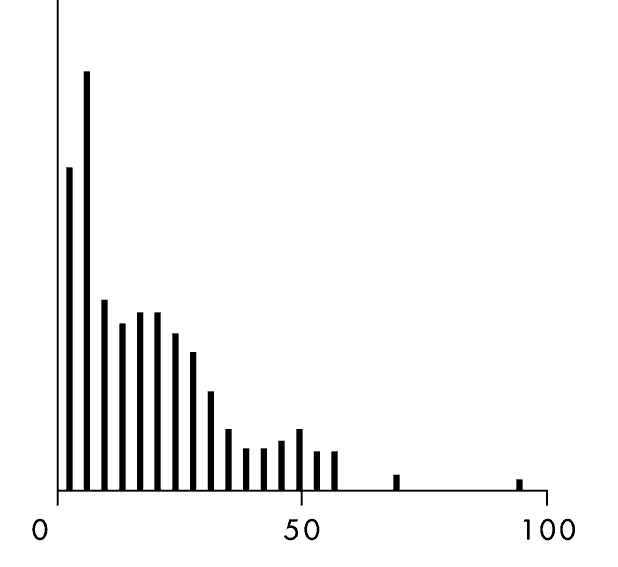
Догадки относительно продолжительности царствования фараона
Эта догадка была бы совершенно верной, если бы речь шла о британском короле, но для египетского фараона она не годилась: 4000 лет назад продолжительность жизни была гораздо короче. Если фараон доживал до 35 лет, его считали чуть ли не стариком! Таким образом, правильный ответ заключается в следующем: фараон, который провел на престоле 11 лет, скорее всего, будет править еще лет 12, а потом умрет от болезни или какой-либо другой распространенной причины смерти в Древнем Египте:
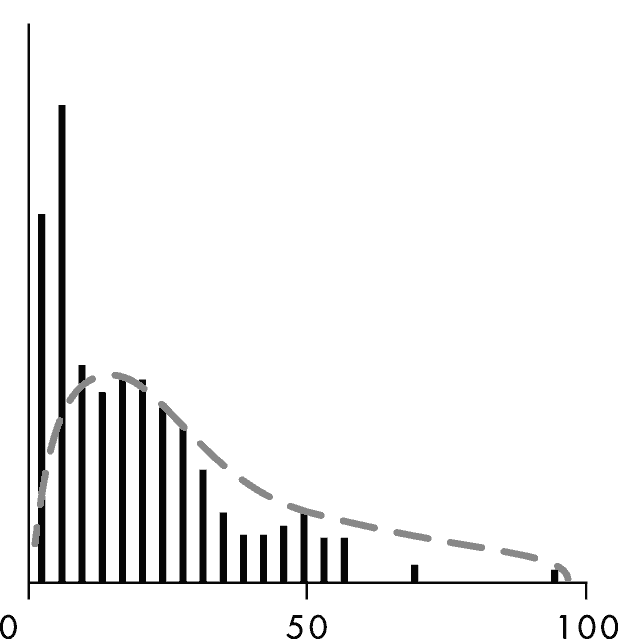
Реальная продолжительность царствования фараона
Студенты рассуждали правильно. Интуиция их не подвела: срок царствования фараона действительно подчиняется распределению Эрланга. Ошибочным оказалось исходное предположение – так называемая априорная вероятность, или «базовая оценка». Поскольку студенты исходили из заведомо неверного представления о продолжительности жизни фараонов, неверными были и их дальнейшие прогнозы.
«Наша способность делать прогнозы на основании минимальной информации и корректировать их с учетом данных из жизни – просто невероятна, – сказал мне Тененбаум. – Но это работает только тогда, когда верна исходная формула».
Как же получить верную «исходную формулу»? Ответ прост: убедиться в полноте своего опыта. Наши предположения базируются на том, с чем мы столкнулись в жизни, но в основе нашего опыта лежит необъективная выборка. В частности, мы склонны запоминать успехи и забывать о неудачах. Многие из нас, например, узнают о мире бизнеса из газет и журналов. Мы чаще ходим в шумные рестораны и смотрим популярные фильмы. Проблема в том, что такой опыт предполагает знакомство преимущественно с одной – успешной – стороной той или иной сферы. Газеты и журналы, как правило, печатают гораздо больше репортажей о молодых компаниях, приобретенных за один миллиард долларов, чем о сотнях аналогичных компаний, которые обанкротились. Мы едва ли обратим внимание на пустой ресторанчик, который находится по дороге в нашу любимую, вечно переполненную пиццерию. Все это заставляет нас предсказывать благополучный исход слишком часто, ибо мы опираемся на опыт и предположения, в которых чересчур велика доля успеха. Промахи-то мы игнорируем.
Многие успешные люди, напротив, тратят огромное количество времени на поиск информации о неудачах. Они специально выискивают статьи о компаниях-банкротах. Они приглашают на обед коллег, которые не получили повышения, и подробно расспрашивают их, что пошло не так. На ежегодных обзорных совещаниях они ждут не только похвалы, но и критики. Они тщательно анализируют выписки по кредитным картам в надежде выяснить, почему, собственно, они не накопили столько, сколько рассчитывали. Возвращаясь домой после работы, они обдумывают совершенные оплошности и не забывают мелкие ошибки. Они спрашивают себя, почему данный конкретный разговор прошел не так, как они хотели, и мысленно прокручивают прошедшее совещание – возможно, им следовало быть более краткими? Все мы от природы склонны быть оптимистами, игнорировать собственные ошибки и забывать незначительные промахи друг друга. Однако любой хороший прогноз опирается на реалистичные предположения, а те, в свою очередь, основываются на нашем опыте. Если мы обращаем внимание только на хорошие новости, мы заведомо ставим себя в невыгодное положение.
«Хорошие предприниматели четко осознают риски, которыми чреваты беседы исключительно с успешными людьми, – утверждает Дон Мур, профессор из Калифорнийского университета в Беркли, специалист по психологии предпринимательства, который принимал участие в проекте „Здравое суждение“. – Они стремятся как можно больше времени проводить в кругу людей, которые жалуются на свои неудачи, – людей, которых большинство из нас, как правило, избегают».
По существу, в этом и заключается один из главных секретов принятия оптимальных решений. В основе хорошего выбора лежит прогнозирование будущего. Точное прогнозирование требует учета как можно большего количества как побед, так и разочарований. Чтобы понять, сколько соберет тот или иной фильм в прокате, нам придется посидеть не только в полных, но и в пустых залах, чтобы точно оценить продолжительность жизни – провести время в кругу детей и стариков, а чтобы развить деловую хватку – побеседовать как с преуспевающими, так и со слабыми руководителями.
Конечно, это трудно, ведь на успех смотреть приятнее. Обычно мы избегаем задавать грубые вопросы коллегам, которых только что уволили, и не решаемся расспрашивать друзей, что именно привело их к разводу. И тем не менее уточнение базовой оценки требует общения не только с состоявшимися людьми, но и с теми, чьи надежды не оправдались.
В общем, когда в следующий раз ваш друг прозевает продвижение по службе, спросите его, как так получилось. Если сорвется сделка, позвоните другой стороне и выясните, что конкретно вы сделали не так. Если у вас выдался плохой день или вы накричали на супруга, не говорите, что завтра все будет иначе, – заставьте себя действительно разобраться в том, что произошло.
В следующий раз используйте полученные знания для прогнозирования будущего. Ни одному человеку не дано знать наверняка, как все обернется в итоге. Но чем больше вы будете представлять потенциальные варианты развития событий, чем точнее научитесь определять, какие предположения верны, а какие надуманны, тем выше будут ваши шансы принять лучшее решение.
Энни многое знает о байесовском мышлении с аспирантуры и постоянно использует его в покере. «Когда я играю против человека, которого никогда не встречала прежде, первое, что я делаю, – я думаю о базовых оценках, – сказала она. – Тем, кто никогда не изучал правило Байеса, может показаться, что я предвзята. Если я играю, скажем, с 40-летним бизнесменом, я предположу, что его беспокоит только одна вещь – похвастаться друзьям, что он играл против профи. Поскольку на самом деле он не очень-то и стремится выиграть, он будет много рисковать. Если напротив меня сидит 22-летний парень в покерной футболке, я предположу, что он учился играть онлайн, а значит, будет действовать сдержанно и осмотрительно».
«Разница между предвзятостью и байесовским мышлением, – продолжала Энни, – заключается в том, что по ходу игры я стараюсь уточнить свои предположения. Если я вижу, что 40-летний бизнесмен превосходно блефует, это может означать, что передо мной профессионал, который надеется, что все его недооценят. С другой стороны, если 22-летний парень будет блефовать каждую раздачу, я, вероятно, сочту, что он – просто богатенький мальчик, который не понимает, что делает. Я трачу много времени на корректировку своих предположений, ведь если они ошибочны, моя базовая оценка никуда не годится».
После выбывания Говарда за столом остаются только два игрока: Энни и Фил Хельмут. Хельмут – живая легенда покер-румов, телевизионная знаменитость по прозвищу The Poker Brat. «Я – Моцарт покера, – сказал он мне. – Я могу читать своих противников лучше, чем кто-либо из игроков, может быть, лучше всех в мире. Это белая магия, инстинкт».
Энни сидит на одном конце стола, Хельмут на другом. «Я отлично представляла, какой видел меня Фил в тот момент, – позже призналась Энни. – Однажды Фил сказал мне, что невысокого мнения о моей креативности. Он сказал, что я больше везучая, чем умная, и боюсь блефовать, когда это действительно важно».
Для Энни это проблема. Она хочет, чтобы Фил думал, будто она блефует. Единственный способ заманить его в игру по-крупному – убедить, что она блефует, когда на самом деле это не так. Чтобы выиграть турнир, Энни должна заставить Фила изменить свои предположения о ней.
У Фила другой план. Он считает, что он сильный игрок. Он считает, что видит Энни насквозь. «У меня есть способность учиться очень, очень быстро, – сказал он мне. – Зная, что делают другие игроки, я могу контролировать стол». Это не хвастовство. Хельмут выиграл 14 чемпионатов по покеру.
У Энни и Фила примерно равное количество фишек. Следующий час они разыгрывают одну комбинацию за другой, но ни один не получает явного преимущества. Фил продолжает тонко подкалывать Энни, пытаясь сбить ее с толку, разозлить, обидеть – все что угодно, лишь бы вывести из равновесия.
– Я бы предпочел играть с вашим братом, – говорит он.
– Все в порядке, – отвечает Энни. – Я в финале, и это главное.
Энни блефует четыре раза. «Я хотела, чтобы он достиг той точки, когда он скажет: „К черту! Она блефует раздачу за раздачей, я должен дать отпор“», – объяснила Энни. Но Фил по-прежнему спокоен. Он не горячится.
Наконец Энни получает комбинацию, которую она так ждала. Дилер дает ей короля и девятку. Фил получает короля и семерку. В центре стола лежат общие карты: король, шестерка, девятка и валет.
Фил знает, что у него пара королей. Но он не знает, что у Энни две пары – короли и девятки. Ни он, ни она не видят карты друг друга.
В ответ на электронное письмо, призванное исключить фактические ошибки, Джонсон писал: «Идея в том, чтобы думать о подмножестве релевантных данных».
Энни поднимает ставку – 120 тысяч долларов. Фил, думая, что его рука – два короля – самая сильная, отвечает. Тогда Энни ставит все свои фишки, и в банке оказывается 970 тысяч долларов.

Теперь очередь Фила.
Он что-то бормочет себе под нос.
– Это невероятно, – говорит он. – На самом деле невероятно. Она, скорее всего, даже не знает, насколько я силен. Я даже не уверен, что она в полной мере осознает силу руки.
Фил встает.
– Не знаю, – произносит он, расхаживая вокруг стола. – Не знаю, у меня дурное предчувствие.
Фил сбрасывает карты.
Он переворачивает своих королей, показывая Энни, что у него была старшая пара. И тут Энни наносит удар: она случайно переворачивает одну из своих карт и показывает Филу пару девяток. О паре королей он ничего не знает.
«Я хотела заставить его изменить свои предположения обо мне, – позже сказала Энни. – Я хотела заставить его думать, будто я блефовала с парой девяток».
– Ничего себе! И ты поставила все с какой-то девяткой? – говорит Фил Энни. – Это так безрассудно, особенно если играешь против кого-то вроде меня. Возможно, я поторопился.
Игроки готовы к следующей раздаче. Фишки Энни – 1 460 000 долларов; фишки Фила – 540 тысяч долларов. Дилер сдает карты. У Энни король и десятка. У Фила десятка и восьмерка. Первые общие карты – 2, 10 и 7.
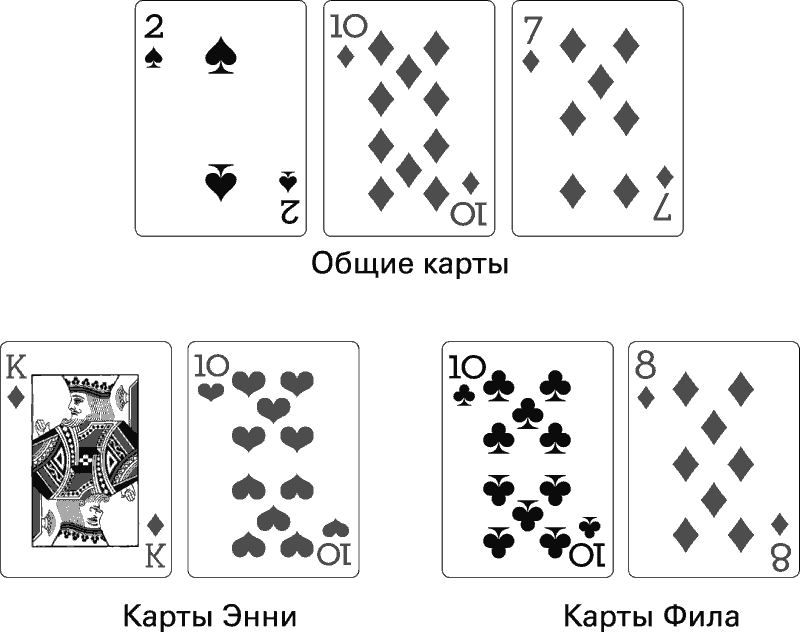
У Фила две десятки и восьмерка. Это хорошая комбинация. У Энни тоже две десятки и король, что немного лучше.
Фил кладет в банк 45 тысяч долларов. Энни поднимает ставку до 200 тысяч. Это агрессивный шаг. Но Фил начинает верить, что Энни играет безрассудно. Он думает, что видит закономерность, которую отнюдь не ожидал: она блефует, и блефует, и блефует. Базовая оценка Фила постепенно меняется.
Фил смотрит на стопку фишек на столе. Может быть, его предположение, что Энни слишком боится, чтобы блефовать в критические моменты, ошибочно? Может быть, Энни блефует прямо сейчас? Может быть, она наконец перегнула палку?
– Ставлю все, – говорит Фил, толкая свои фишки на середину стола.
– Отвечаю, – заявляет Энни.
Игроки открывают карты.
– Дерьмо, – ругается Фил, видя, что у них обоих по две десятки. Но если вторая карта Фила – восьмерка, то у Энни – король.
Дилер кладет на стол семерку, которая не дает преимущества ни одному из игроков.

Энни стоит, прижимая руки к щекам. Фил тоже вскакивает.
– Дайте мне восьмерку, – шепчет он. Это единственная карта, которая может его спасти. Дилер открывает последнюю общую карту. Это тройка.
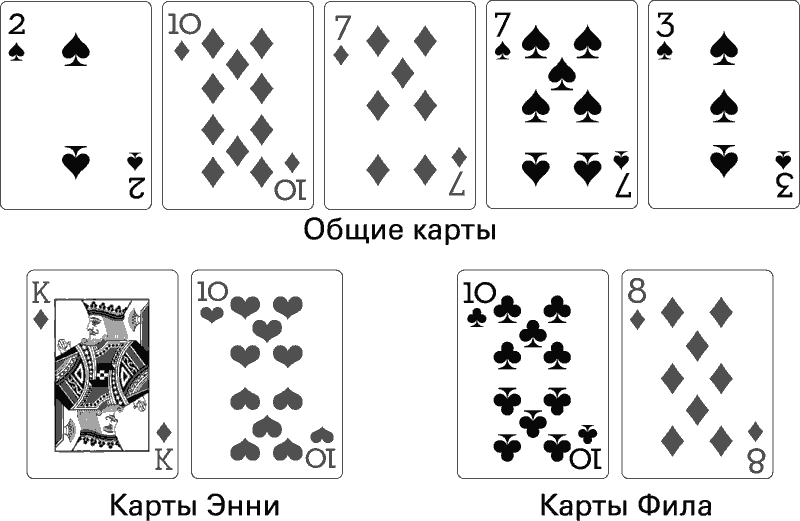
Энни выигрывает два миллиона долларов. Фил выбывает из турнира. Игра окончена. Энни – чемпион.
Позже она скажет, что победа в этом турнире изменила ее жизнь. Фактически она стала самой знаменитой женщиной, которая когда-либо играла в покер. В 2010 году она выиграла престижный турнир «National Heads-Up Poker Championship». Сегодня она занимает первое место по прибыли в Мировой серии покера. В общей сложности Энни выиграла более четырех миллионов долларов. Она больше не беспокоится об ипотеке. Ее не мучают приступы паники. В 2009 году она появилась в шоу «Celebrity Apprentice». Перед началом съемок она нервничала, но не сильно. Срывов больше не было. Последнее время она мало играет на турнирах. Большую часть времени Энни читает лекции. Эти лекции посвящены вероятностному мышлению, неопределенности и роли байесовского подхода в принятии оптимальных решений в повседневной жизни.
«В покере многое зависит от удачи, – сказала мне Энни. – Как и в жизни. Никогда не знаешь, чем все закончится. Когда на втором курсе я легла в психиатрическую больницу, я и представить не могла, что в конечном итоге стану профессиональным игроком в покер. Вы точно не знаете, к чему все идет, но с этим нужно смириться. Так я избавилась от тревоги. Все, что мы можем сделать, – это научиться принимать наилучшие решения здесь и сейчас и надеяться, что со временем шансы окажутся в нашу пользу».
Как же научиться принимать хорошие решения? Отчасти путем тренировки вероятностного мышления. Для этого мы должны представить различные варианты развития событий – иными словами, удерживать в сознании несколько противоречивых сценариев одновременно – после чего проанализировать широкий спектр успешных начинаний и неудач. Интуиция подскажет нам, какие прогнозы сбудутся скорее всего.
Развить такого рода интуицию можно различными способами: изучая статистику, играя в покер, размышляя над потенциальными подводными камнями и факторами успеха, помогая собственным детям справиться со своими страхами – изложить их на бумажке и терпеливо подсчитать вероятность того, что все эти «ужасные события» действительно произойдут. Существует множество способов развить байесовский инстинкт. Некоторые из них на удивление просты – достаточно взглянуть на свои прошлые решения и спросить себя: почему я был так уверен, что все будет именно так? Почему я оказался не прав?
Какой бы метод мы ни избрали, цель всегда одна: представить будущее как множество возможностей, а не один заранее определенный исход; установить, что известно, а что нет, найти вариант, который предполагает наилучшие шансы. Предсказать будущее нереально. Никто не может предсказать завтра с абсолютной уверенностью. Поэтому некоторые люди избегают каких-либо прогнозов вообще: их жажда уверенности слишком сильна, а страх сомнения невыносим.
Если бы Энни осталась в университете, пригодилось бы ей все это? «Безусловно, – сказала она. – Допустим, вы выбираете работу. Прикидываете, можете ли позволить себе съездить в отпуск. Решаете, сколько вам нужно отложить на пенсию. Все это – прогнозы». Здесь действуют те же самые основные правила. Чтобы принять лучшее решение, необходимо представить различные варианты будущего, а затем спросить себя, какие из этих вариантов кажутся наиболее вероятными и почему. Во всяком случае, так поступают люди, которые умеют делать правильный выбор.
Любой человек может научиться принимать оптимальные решения. Мы все можем приучить себя замечать прогнозы, которые делаем каждый день. Конечно, никто не застрахован от ошибки. И все-таки, потренировавшись, мы можем научиться влиять на вероятность того, что наше предсказание сбудется.

