В 2011 году Управление директора Национальной разведки обратилось к нескольким университетам с просьбой принять участие в некоем проекте «с целью существенного повышения надежности, точности и своевременности прогнозов разведки». Получив соответствующий грант, каждый факультет должен был набрать команду специалистов по международным делам, после чего попросить этих специалистов сделать ряд прогнозов о будущем. Исследователям предстояло определить, кто дал наиболее точные прогнозы, а главное – как они это сделали. Выводы, надеялось правительство, помогут аналитикам ЦРУ лучше выполнять свою работу.

Большинство университетов, принявших участие в программе, выбрали стандартный подход. Они обратились к профессорам, аспирантам, исследователям в сфере международной политики, а также к другим ученым и задали этим специалистам вопросы, на которые никто не знал ответов, – возобновит ли Северная Корея переговоры по вооружениям к концу года, получит ли партия «Гражданская платформа» большинство мест на парламентских выборах в Польше и тому подобное. Изучение различных подходов, думали все, подкинет ЦРУ свежие идеи.

Два университета, однако, избрали другую тактику. Группа психологов, статистиков и политологов из Пенсильванского и Калифорнийского университетов в Беркли использовали правительственные деньги иначе. Ученые решили выяснить, можно ли научить прогнозированию обывателей. Данное исследование получило название «Проект „Здравое суждение“» («Good Judgment Project»). Вместо того чтобы нанимать специалистов, ученые обратились к тысячам обычных людей – юристам, домохозяйкам, студентам, любителям читать газеты, фактически ко всем, кто имел высшее образование, – и организовали интернет-классы по прогнозированию, в рамках которых желающих обучали разным способам думать о будущем. По окончании тренинга участники должны были ответить на те же вопросы касательно внешней политики, что и эксперты.

В течение двух лет исследователи проводили тренинги и собирали данные. Помимо отслеживания результатов, особый интерес представляли изменения производительности в зависимости от типа обучения. В конце концов был опубликован следующий вывод: даже краткий тренинг в области исследовательских и статистических методов – обучение различным способам думать о будущем – повышал точность предсказаний. При этом наиболее эффективным способом развить способность к прогнозированию оказался определенный вид урока – а именно, обучение вероятностному рассуждению.

На занятиях по вероятностному рассуждению участников учили думать о будущем не как о том, что должно произойти, а как о серии возможностей, которые могут произойти. Их учили представлять будущее в виде массива потенциальных исходов разной вероятности. «Большинство людей крайне небрежно подходят к вопросу о будущем, – сказал Лайл Ангер, профессор информатики из Пенсильванского университета, который помогал наблюдать за ходом проекта „Здравое суждение“. – Они часто говорят что-то типа: „Вероятно, в следующем году мы поедем отдыхать на Гавайи“. Ну? И что это значит? Они в этом уверены на 51 процент? Или на 90 процентов? А ведь это важно, если вы покупаете билеты, не подлежащие возврату». Цель вероятностного обучения – научить людей преобразовывать интуицию в статистические вероятности.

В рамках одного из упражнений, например, участники должны были проанализировать вопрос: «Будет ли президент Франции Саркози переизбран в 2012 году?»

Чтобы предсказать шансы на переизбрание Николя Саркози, требовалось рассмотреть минимум три переменных. Первая переменная – это срок пребывания в должности. Предыдущие выборы во Франции показали, что действующий президент – например президент Саркози – в среднем может рассчитывать на получение 67 % голосов. Следовательно, на основании этих данных вероятность того, что Саркози останется на своем посту, составляла 67 %.

Но были и другие переменные, которые следовало учесть. В последнее время Саркози не пользовался популярностью среди французских избирателей. Социологи подсчитали, что из-за низких рейтингов шансы на переизбрание Саркози на самом деле составляют 25 %. Иными словами, вероятность того, что Саркози уже не будет президентом, равнялась 75 %. Кроме того, французская экономика на тот момент находилась в весьма плачевном состоянии. Со своей стороны, экономисты полагали, что Саркози наберет только 45 % голосов.

Итого, от участников требовалось рассмотреть три потенциальных будущих: Саркози мог получить 67 %, 25 % или 45 % голосов. В первом случае он выиграет выборы легко, во втором проиграет с большим отрывом, а в третьем проиграет с минимальным отрывом. Как же сочетать эти противоречивые результаты в одном прогнозе? «Нужно усреднить оценки, сделанные на основании данных предыдущих выборов, рейтингов одобрения и темпов экономического роста, – говорили на тренинге. – В отсутствие веских оснований считать одну переменную важнее другой, считайте их равновесными. Используя этот подход, мы получаем [(67 % + 25 % + 45 %) / 3] = 46 %. То есть шансы на переизбрание Николя Саркози составляют 46 %».

Девять месяцев спустя Саркози набрал 48,4 % голосов и уступил пост президента Франсуа Олланду.

Это самый базовый вид вероятностного мышления – упрощенный пример, который учит основной идее: противоречивые варианты развития событий можно объединить в единый прогноз. Специалисты, как правило, представляют различные исходы в виде вероятностных кривых – графиков, показывающих распределение потенциальных вариантов. Так, отвечая на вопрос «сколько мест получит партия Саркози во французском парламенте», эксперт может описать возможные результаты в виде кривой, которая отражает связь между количеством мест в парламенте и шансами Саркози остаться президентом:

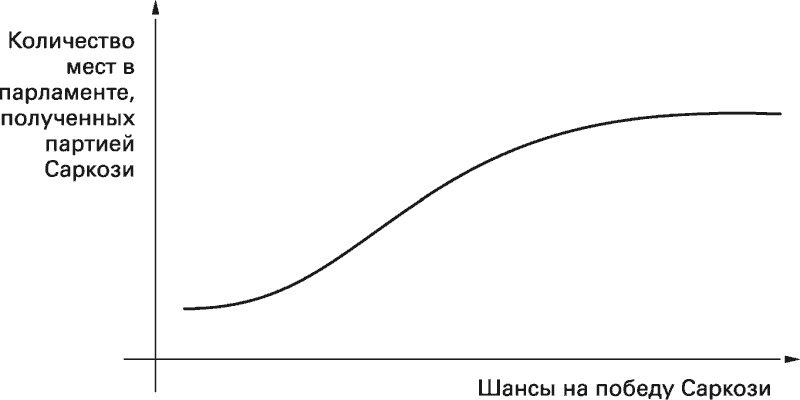
В действительности, когда Саркози проиграл выборы, его партия, Union pour un mouvement populaire, или UMP, получила лишь 194 места – то есть значительно меньше, чем на предыдущих выборах.

Учебные модули проекта «Здравое суждение» включали разнообразные методы объединения вероятностей и сравнения альтернативных вариантов будущего. Впрочем, на протяжении всего курса обучения участникам без конца повторяли одну и ту же основную идею. Будущее – это не что-то одно. Скорее, это множество вариантов, которые часто противоречат друг другу, пока один из них не сбудется. Все варианты можно объединить и предсказать, какой из них наиболее вероятен.

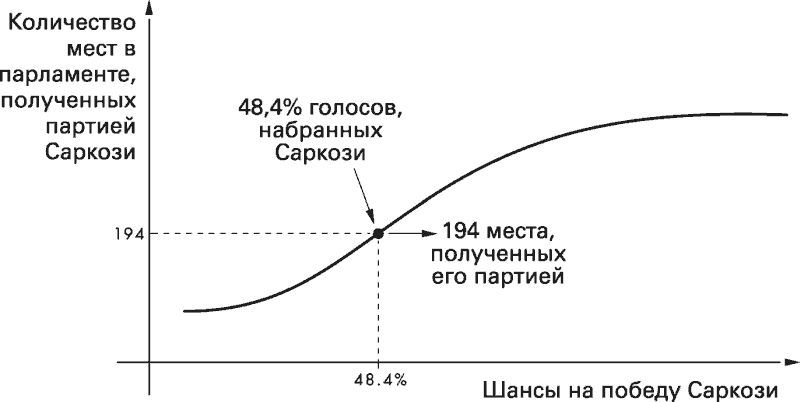
Это и есть вероятностное мышление – способность удерживать в уме несколько противоречивых возможностей и оценивать их относительную вероятность. «Мы не привыкли думать о нескольких будущих, – сказала Барбара Меллерс, руководитель проекта „Здравое суждение“. – Мы живем только в одной реальности, а потому представление о будущем, как о многочисленных возможностях, может вызвать дискомфорт, ибо в этом случае мы вынуждены думать о разных вещах, в том числе и тех, которые, как мы надеемся, не сбудутся никогда».

Как сообщают исследователи, обучение вероятностному мышлению привело к 50-процентному повышению точности прогнозов. «Команды, прошедшие курс обучения, показали наилучшие результаты, – отметил сторонний наблюдатель. – Главным образом, их учили преобразовывать интуитивные догадки в вероятности. Каждый день команда проводила онлайн-обсуждения и корректировала свои предположения… Грандиозные теории, скажем, о природе современного Китая были совершенно бесполезны. Способность рассмотреть узкий вопрос с различных позиций и быстро скорректировать степень вероятности того или иного исхода – вот что было самое главное».

Мышление сквозь призму вероятностей требует от нас способности усомниться в собственных предположениях и умения мириться с неопределенностью. Чтобы научиться лучше предсказывать будущее – другими словами, принимать оптимальные решения, – мы должны отличать наши надежды от фактической вероятности того или иного события. К сожалению, это не всегда одно и то же.

«Если вы на сто процентов уверены, что в данный конкретный момент любите свою подругу – это, конечно, прекрасно. Но если вы планируете сделать ей предложение, разве вы не захотите узнать, каковы шансы остаться с ней в браке в течение следующих тридцати лет? – говорит Дон Мур, профессор школы бизнеса Хасс в Беркли. – Разумеется, я не могу сказать точно, сохраните ли вы влечение друг к другу через тридцать лет. Зато я могу рассчитать вероятность, что вы будете по-прежнему любить друг друга, а также привести статистические данные о влиянии рождения детей на отношения между супругами. Получив эти сведения, вы проанализируете вероятности с учетом личного опыта и собственных представлений о том, что произойдет скорее всего. Это поможет вам спрогнозировать будущее чуточку точнее».

«С точки зрения перспективы, – продолжает Мур, – такие прогнозы весьма ценны: несмотря на то, что вы на сто процентов уверены, что любите эту женщину сейчас, вероятностный подход к будущему заставит вас задуматься о вещах, которые пока не столь очевидны, но в дальнейшем очень важны. Вероятностное мышление вынуждает вас быть честным с самим собой – в том числе признаться, что кое в чем вы не уверены».

Когда Энни увлеклась покером всерьез, брат объяснил ей, что отличает победителей от всех остальных. Неудачники, сказал Говард, всегда ищут определенности. Победители охотно признают, что они не знают то-то и то-то. В самом деле, если вы знаете, что именно вы не знаете, – это огромное преимущество, которое можно использовать против других игроков. Когда Энни звонила Говарду и жаловалась, что проиграла, что ей не повезло, что карты выпали плохие, брат неизменно повторял одно и то же: перестань ныть.

«А тебе не приходило в голову, что ты и есть тот идиот, который жаждет определенности?» – спрашивал он.

В техасском холдеме – разновидности покера, в который играла Энни, – каждый игрок получает две закрытые карты, после чего на середину стола сдают пять общих карт. Победителем становится тот, кто составит наилучшую комбинацию из своих и общих карт.

Когда Говард только учился играть, сказал он Энни, его противниками были маклеры с Уолл-стрит, чемпионы мира по бриджу и прочие отборные фанаты математики. За одну ночь из рук в руки перетекали десятки тысяч долларов. Обычно компания засиживалась до рассвета, а потом шла завтракать. За завтраком разбирали сыгранные комбинации. В конечном итоге Говард пришел к выводу, что самая сложная часть покера – вовсе не математика. Потренировавшись, любой может научиться запоминать шансы или рассчитывать возможность забрать банк. Нет, самое сложное – это научиться делать выбор, основываясь на вероятностях.

Допустим, вы играете в техасский холдем. У вас на руках червовая дама и червовая девятка. Дилер кладет на стол четыре общие карты.

Предстоит открыть еще одну карту. Если последняя карта окажется червой, у вас получится флеш или пять черв. Это сильная комбинация. Быстрый мысленный расчет говорит следующее: поскольку в колоде 52 карты и 4 червы уже открыты, значит, остается 9 черв и 37 не-черв. Иными словами, есть 9 карт, которые дадут флеш, и 37 карт, которые не дадут флеш. Шансы на получение флеша, таким образом, составляют 9 к 37, то есть примерно 20 %.

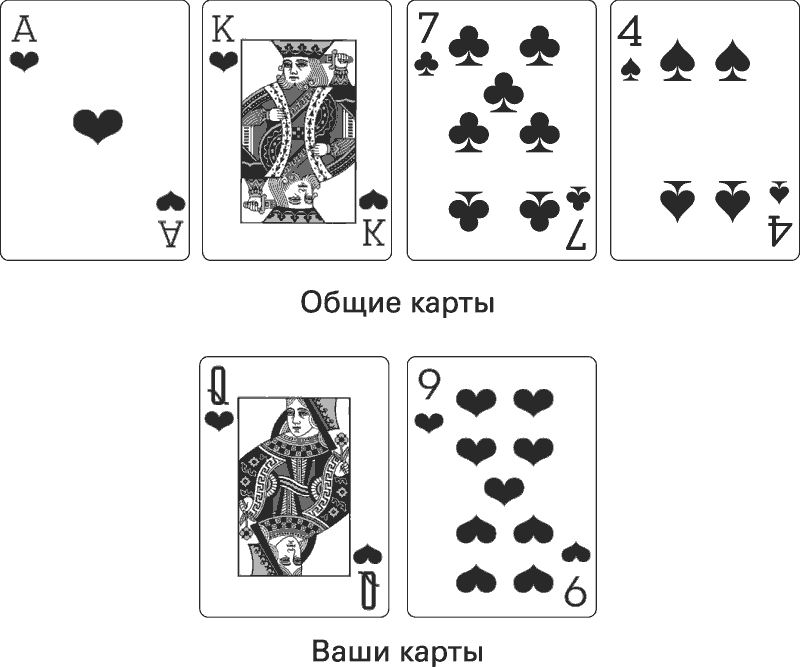
Иначе говоря, вероятность того, что вы не соберете флеш и можете потерять деньги, равна 80 %. Начинающий игрок, скорее всего, сбросит карты. Это потому, что новичок ориентируется на определенность: шансы на флеш в данном случае относительно невелики. Вместо того чтобы ставить деньги на маловероятный исход, он предпочтет выйти из игры.

Эксперт видит эту игру по-другому. «Опытный игрок в покер не думает об определенности, – сказал брат Энни. – Он хочет знать, что ему известно, а что нет».

Допустим, эксперт получает даму и девятку червей и надеется на флеш. Если его оппонент ставит 10 долларов, в результате чего общий банк доходит до 100 долларов, он приступает к вычислению второго набора вероятностей. Чтобы остаться в игре – и посмотреть, окажется ли последняя карта червой, – эксперт должен всего-навсего ответить на последнюю ставку. Если он поставит 10 долларов и соберет флеш, то выиграет 100 долларов. «Шансы банка» составляют 10 к 1: в случае выигрыша он получит 10 долларов за каждый доллар, которые поставит сейчас.

Теперь опытный игрок может сравнить шансы, представив эту же руку сто раз. Он не знает, выиграет он или проиграет именно эту руку, но он знает, что, если он сыграет ее сто раз, то, в среднем, выиграет 20 раз. Каждая победа принесет ему 100 долларов. Итого, получается 20 раз по 100 долларов, или 2000 долларов.

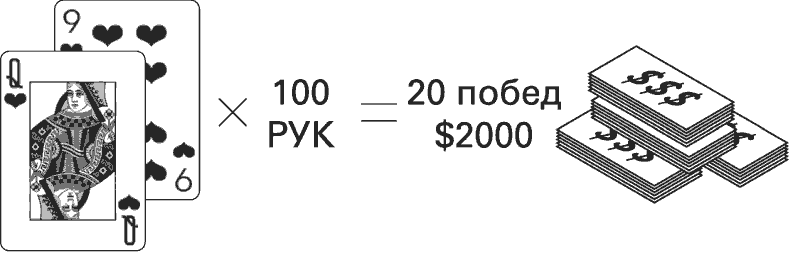
Еще опытный игрок знает, что сыграть 100 рук будет стоить ему всего 1000 долларов (потому что каждый раз он ставит всего 10 долларов). Таким образом, даже если он проиграет 80 раздач, то все равно положит в карман 1000 долларов (что соответствует выигрышу в размере 2000 долларов за вычетом 1000 долларов, необходимых для участия в игре).

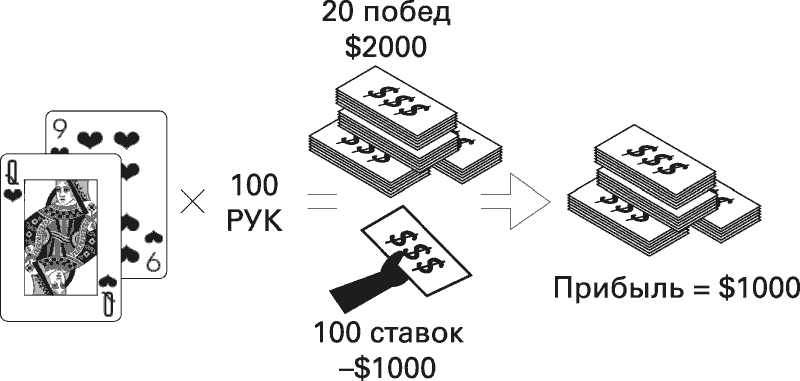
Понятно? Если нет – ничего страшного. Суть в том, что вероятностное мышление подсказывает эксперту, как быть дальше. Он понимает, что многое предсказать не в силах. Но если он сыграет эту же руку 100 раз, то наверняка станет на 1000 долларов богаче. Поэтому опытный игрок делает ставку и остается в игре. С вероятностной точки зрения ставка со временем окупится. Неопределенность исхода именно этой руки не имеет значения. Что важно – так это шансы, которые в долгосрочной перспективе принесут победу.

«Большинство игроков зациклены на определенности, и это оказывает значимое влияние на их выбор, – сказал Энни ее брат. – Быть великим игроком означает принимать неопределенность. Пока неопределенность тебя не беспокоит, шансы будут работать на тебя».

Итак, Грег Реймер выбывает. Брат Энни, Говард, играет на этом турнире чемпионов рядом с сестрой. За последние двадцать лет Говард зарекомендовал себя в качестве одного из лучших игроков в мире. У него два браслета Мировой серии покера и миллионные выигрыши. В начале турнира Энни и Говарду повезло: пока им нечасто доводилось напрямую соперничать за крупный банк. Теперь же, семь часов спустя, количество игроков сократилось, и им неизбежно придется играть друг против друга.

Первым выбыл Грег, которого погубило обыкновенное невезение. Дойл Брансон, 71-летний девятикратный чемпион, вышел из игры из-за рискованной попытки удвоить свои фишки. Фил Айви, который выиграл свой первый турнир Мировой серии покера в 24 года, был выбит Энни, положившей туза и даму против его туза и восьмерки. Они играют уже 12 часов; куча фишек Энни выросла, потом уменьшилась, затем снова выросла. Сейчас за столом сидят только Энни, Говард и мужчина по имени Фил Хельмут. «Тренировочный» обмен фишками длится уже 90 минут – пока они только присматриваются друг к другу. И тут Энни получает пару шестерок.

Она начинает прикидывать, что она знает и чего не знает. Она знает, что у нее сильные карты. Она знает, что если сыграет эту руку 100 раз, то останется в плюсе. «Иногда, когда я учу людей играть в покер, я говорю им, что бывают ситуации, когда нужно сначала сделать ставку, и только потом смотреть свои карты, – сказала мне Энни. – Если шансы банка в вашу пользу, вы всегда должны делать ставку. Просто примите это за правило».

Говард, ее брат, похоже, доволен своей комбинацией, потому что он кладет в банк все свои фишки, 310 тысяч долларов. Фил Хельмут сбрасывает карты. Ставка за Энни.

– Принимаю, – говорит она.

Оба открывают карты. У Энни две шестерки.

У Говарда две семерки.

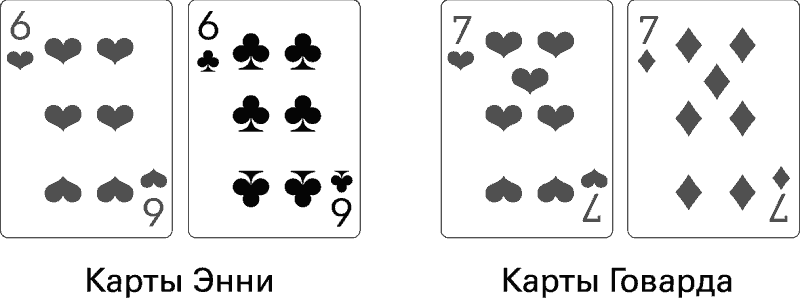
– Хорошая рука, – говорит Энни.

Шансы на победу Говарда составляют 82 %. Если Говард выиграет, он заберет более 500 тысяч долларов и станет чип-лидером. С вероятностной точки зрения оба сыграли совершенно верно. «Энни сделала правильный выбор, – позже сказал мне Говард. – Она просчитала шансы и не ошиблась».

Дилер открывает первые три общие карты.

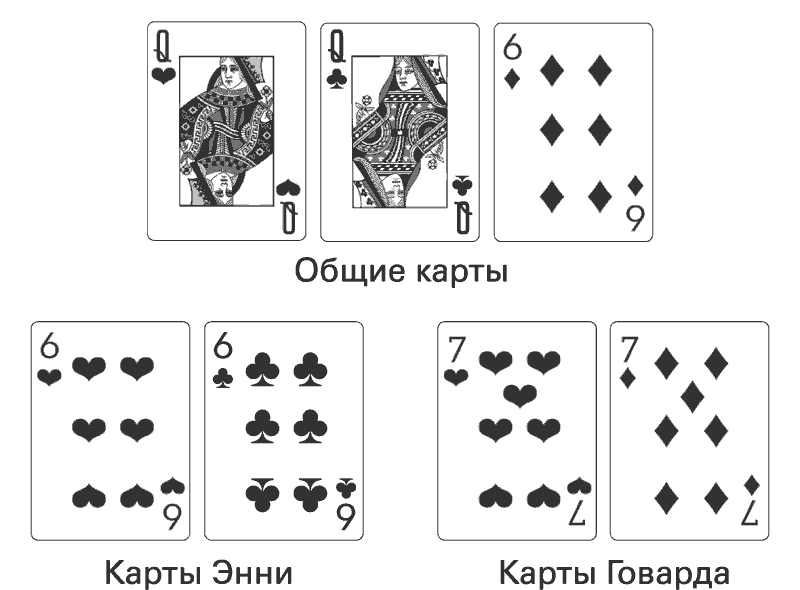
– О боже! – восклицает Энни и закрывает лицо руками. – О боже!

Шестерка и две дамы в числе общих карты дают Энни фул-хаус. Если Энни и Говард сыграют эту руку 100 раз, Говард, скорее всего, выиграет 82 раза. Но не сейчас. Дилер кладет на стол две оставшиеся карты.

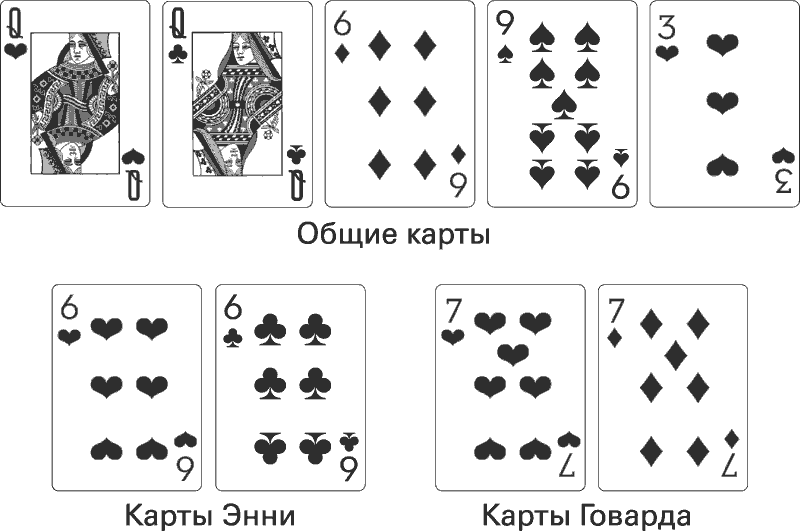
Говард выбывает из игры.

Энни вскакивает со стула и обнимает брата.

– Мне очень жаль, Говард, – шепчет она и, всхлипывая, выбегает из студии.

– Все нормально, – говорит Говард, найдя ее в холле. – Просто побей Фила.

«Вы должны научиться жить с этим, – позже сказал мне Говард. – Я только что прошел через это с собственным сыном. Он подал заявления в несколько колледжей и страшно нервничал. В итоге мы составили список из двенадцати школ, разделив их на три группы. В школы из первой группы он попадал наверняка, из второй группы – 50 на 50, а из третьей группы – с большой натяжкой. Потом мы сели и начали рассчитывать вероятности».

Проанализировав статистику, которую эти школы публиковали в интернете, Говард и его сын рассчитали вероятность попадания в каждый из колледжей. Затем они сложили все вероятности вместе. Это была довольно простая математика, доступная даже магистру английского языка, при условии, конечно, что он умеет пользоваться Гуглом. Они выяснили, что шанс попадания по меньшей мере в одну школу равнялся 99,5 %, а шанс попадания в хорошую школу превышал 50 %. К сожалению, вероятность того, что сын Говарда попадет в одну из престижных школ, которые ему так понравились, оказалась весьма невелика. «Это было печально, но, посмотрев на цифры, он немного успокоился, – сказал Говард. – Возможно, он не попадет туда, куда хочет, но уж куда-нибудь его точно возьмут».

«Вероятности ближе всего к предсказаниям, – пояснил Говард. – Нужны силы, чтобы жить с мыслью о том, что может произойти».