Глава 5
Почему важна гибкость, а не скорость
Ошибочные идеи, несовершенные методы преподавания и ложные установки ограничивают возможности обучения. Однако теперь мы вооружены данными научных исследований и располагаем большим выбором диаметрально противоположных и доказанных образовательных методик, которые раскрепощают процесс обучения и раскрывают потенциал человека. Выше мы обсудили два пагубных мифа: 1) возможности мозга изначально заданы и неизменны; 2) трудности в обучении свидетельствуют о слабости ученика. Отбрасывая эти ложные идеи, люди претерпевают глубокую трансформацию.
В этой главе мы рассмотрим еще один деструктивный миф — идею о том, что для успешного изучения математики или другого предмета необходимо быстро соображать, — и разберем его альтернативу. Оставляя в стороне теорию о том, что важна одна лишь скорость, и рассматривая обучение как среду для глубокого и гибкого мышления, мы начинаем по-новому воспринимать мир. Как мы обсуждали в , гибкое сознание и способность мыслить творчески присущи новаторам и становятся доступными и нам, когда мы смотрим на известное под другим углом.
Ключевой навык обучения № 5
Скорость мышления не является мерой способностей.
Оптимальное обучение возможно, если подходить к теориям и к жизни в целом гибко и творчески.
Математика более, чем другие предметы, пострадала от идеи, что для достижения успеха нужна быстрая реакция. Частично это следствие порочной школьной практики, например проверки знаний на время, которую часто проводят даже с пятилетними детьми. Родители также практикуют занятия по математике с ограничением по времени, используя, к примеру, дидактические карточки. Из-за этого у многих людей математика ассоциируется со скоростью и они думают, что если не могут быстро оперировать цифрами, то им не преуспеть в этой дисциплине. Своей аудитории я показываю рабочие таблицы, подобные этой (рис. 5.1).

Рис. 5.1. Таблица умножения на 12
Часто такие задания вызывают волну недовольства, хотя некоторым (а их меньшинство) нравятся тесты. Теперь мы знаем, что у многих детей младшего возраста тесты на время формируют негативный опыт при изучении математики. Новые исследования возможностей мозга помогают понять процессы, благодаря которым это происходит.
Влияние стресса и тревоги
Нейробиолог Сиан Байлок изучала мозг людей, работавших в стрессовой обстановке. Она показала, что, когда мы нервничаем или работаем в состоянии стресса, кратковременная память блокируется и мы не можем получить доступ к математическим фактам, которые нам известны. Особенно подвержены риску учащиеся с хорошо развитой кратковременной памятью. Выполняя тесты на время, они испытывают тревогу, что блокирует их кратковременную память и не позволяет прорешать задания. Развивается тревога, а следом за ней запускается сценарий деструктивных установок.
Вам, вероятно, знакомо состояние стресса, затрудняющее работу мозга? Вам когда-нибудь приходилось производить математические расчеты под давлением, когда вы чувствовали, будто в голове пусто? Когда детям младшего возраста предлагают тесты на время, многие начинают нервничать, кратковременная память блокируется — и они не могут выполнить элементарные действия. Если дети понимают, что не справляются с заданием, состояние тревоги только усиливается.
Я много лет преподавала в Стэнфордском университете, и каждый год значительная часть моих студентов испытывала подобную тревогу и страх. Я всегда расспрашивала тех, кто получил подобную психологическую травму, когда и что именно с ними произошло. Почти все опрошенные отвечали одинаково: вспоминали математические тесты на время во втором или третьем классе. Они испытывали беспокойство и, в отличие от других, не справлялись с заданиями, что заставляло их думать (и это неудивительно), будто математика требует скорости и оперативности. В итоге интерес к этой дисциплине они утрачивали.
Преподаватель Джоди Кампинелли рассказала, как в детстве ее изматывала необходимость решать тесты на время, ведь делала она это с трудом. В конце второго класса девочке сообщили, что ей, возможно, придется остаться на второй год, потому что она не справилась с ними. Первая часть истории ужасает, но это еще не все. Джоди сказали, что с ней будет заниматься сам директор школы, которого она называла «мучителем». Вдобавок родители заставляли ее вечерами сидеть на кухне и решать тесты на время; рядом ставили таймер, который громко тикал, пока она лихорадочно пыталась справиться с вычислениями.
Я холодею при мысли о второкласснице, испытывавшей такой стресс. Девочке внушили, что результаты тестов по математике характеризуют ее умственные способности и ценность как личности, после чего сообщили, что она не справилась с заданием. Пытаясь уложиться в отведенное на решение время (а это ей удавалось редко), она нервничала, торопилась — и делала ошибки. Мать же говорила, что ничего страшного не произошло, поскольку тоже не была сильна в математике. И я не удивлена, что Джоди до сих пор вздрагивает от страха при звуке кухонного таймера.
Во втором классе Джоди слышала много негативных высказываний в свой адрес. Например, мать подтверждала отсутствие у дочери способностей к математике — и, разумеется, делала это из самых лучших побуждений. Проведенное Сиан Байлок исследование выявило любопытные закономерности, свидетельствующие о пагубности подобных высказываний. В другом исследовании Сиан вместе с коллегами выяснила, что школьные успехи детей можно спрогнозировать, исходя из количества негативного опыта в математике, о котором вспоминают их родители. В данном случае помехой служит не объем математических знаний родителей, а исключительно их тревожность. Причем родительский негативный опыт в математике отрицательно влиял на учащихся только в том случае, если они помогали детям выполнять домашние задания. Очевидно, что если родители, пережившие такой опыт, не решают задачи вместе со своими детьми, то эта тревога не передается школьникам. В противном случае, вероятно, родители донесут до детей, что математика — это трудно или что у них нет способностей, или, что еще хуже, усадят их на кухне решать задачи с таймером.
Байлок и коллеги также установили, что по объему негативного опыта в математике, который переживают женщины — учительницы начальных классов, можно предугадать успеваемость их учеников, но только девочек, а не мальчиков. Полагаю, такой результат объясняется тем, что преподавательницы делятся своими ощущениями по поводу математики, используя фразы, звучащие как само собой разумеющееся: «В школе у меня не было способностей к математике», а также «Давайте просто пробежимся по этим заданиям и перейдем к чтению». На девочек это влияет намного сильнее, чем на мальчиков, поскольку они идентифицируют себя с учителями своего пола. Оба исследования показывают: отношение к математике со стороны родителей и учителей может снизить успеваемость учащихся, что еще раз подчеркивает взаимосвязь наших убеждений и достижений.
К счастью, за время учебы в школе Джоди получила и положительный опыт. Она поняла, какое разрушительное влияние имеет упор на скорость, и теперь, работая учителем математики в средних и старших классах, считает, что важно именно медленное и глубокое размышление. Со временем Джоди осознала, что глубину ее знаний нельзя измерить кухонным таймером и что скорость не имеет ни малейшего значения.
Скорость с точки зрения нейробиологии
Итак, мы выяснили, что ученики теряют интерес к математическому и научному мышлению из-за того, что не могут выдавать решения быстро и в состоянии стресса. Ирония здесь состоит в том, что математика не тот предмет, где требуется скорость. Некоторые выдающиеся математики-теоретики весьма неспешно выполняют действия с цифрами и другие математические операции. Они мыслят не быстро, а медленно и глубоко.
Некоторые величайшие математики мира, в том числе получившие Филдсовскую премию, например Лоран Шварц и Мариам Мирзахани, открыто говорили о том, насколько медленно они думают обо всем, что касается математики. После получения Филдсовской премии Шварц написал автобиографию о своих школьных годах, где рассказал, что в школе чувствовал себя глупым, потому что был одним из самых медленно думающих учеников. Вот что он говорит.
Я всегда сомневался в своих интеллектуальных способностях и сообразительным себя не считал. Правда в том, что я был и остаюсь достаточно медлительным. Чтобы ухватить суть чего-либо, мне необходимо время, поскольку я всегда стремлюсь понять все до конца. К окончанию одиннадцатого класса я втайне считал себя довольно глупым. Это меня долго беспокоило.
Я все такой же медлительный… В конце одиннадцатого класса я оценил ситуацию и пришел к выводу, что скорость нельзя считать точным показателем интеллекта: важно глубоко понимать суть вещей и их взаимосвязь друг с другом. В этом и состоит интеллект. И не имеет значения, быстро ты соображаешь или медленно.
Во время учебы в школе я соображала быстро, к большому неудовольствию моей учительницы в десятом классе. Каждый день она начинала занятия с того, что писала на доске примерно 80 вопросов. В это время я развлекалась тем, что находила решение с той же скоростью, с которой она писала. Когда учительница клала мел и оборачивалась к классу, я уже заканчивала работу и отдавала ей тетрадь с решениями. Ей не нравились такие темпы, и однажды она сказала, будто я делаю это, чтобы позлить ее (в этой фразе есть над чем задуматься). Она проверяла мою работу в надежде, что там есть ошибки, но я не помню ни одной. Если бы я могла перенестись в те времена со знанием, которым обладаю сейчас, то обратила бы внимание своей учительницы на то, что так быстро находила ответы на вопросы только потому, что они не требовали глубоких или сложных размышлений. Но, скорее всего, это не сошло бы мне с рук.
Быстро расправляясь с задачами по математике, я действовала в соответствии с мифом о том, что скорость — это главное. Неудивительно, что в нашей архаичной системе школьного образования миллионы учеников убеждены в том, что ценится именно быстрое выполнение заданий. Спустя много лет я научилась искать решение разными способами. Теперь я рассматриваю математические задачи не с точки зрения быстроты решения, а как повод для глубокого и творческого размышления. Эта перемена была мне во благо. Сегодня я извлекаю больше пользы не только из размышлений над математическими задачами, но и из чтения научной или технической литературы или работы в данных областях. Смена подхода очень помогла мне и подпитала мое желание помочь другим в том, чтобы развенчать этот вездесущий миф и прийти к пониманию, креативному осмыслению и установлению логических взаимосвязей.
Врач Норман Дойдж считает, что когда люди что-либо быстро осваивают, то предположительно укрепляют уже существующие нейронные связи. Он характеризует их известной английской поговоркой «Легко пришло — легко ушло», ведь эти связи можно ослабить или разрушить. Смотрите, что происходит, когда мы готовимся к тестам и повторяем уже пройденное. Мы загружаем себя информацией, через пару дней воспроизводим ее, но испытание длится недолго — и мы быстро забываем выученное. Более устойчивые изменения в мозге происходят при образовании новых структур, а именно при физическом росте нейронных связей и синапсов. Этот процесс всегда небыстрый.
Дойдж ссылается на исследование людей, изучающих азбуку Брайля. Ученые отметили, что в этом случае мозг сразу начинает быстро развиваться, однако более медленное, глубокое и устойчивое развитие занимает гораздо больше времени. Обучение длилось месяцами.
Если по ощущениям ваш разум похож на решето и вы не в состоянии что-то удержать в памяти, Дойдж рекомендует продолжать попытки — более глубокое понимание придет позже. Он считает, что «тугодумы», кажущиеся слишком медлительными, могут усваивать что-либо лучше «торопыг», которые учатся галопом по Европам и не обязательно сохраняют полученные знания без постоянного повторения.
Когда одни ученики постигают премудрости науки медленно, а другие быстро, то учителя часто делают вывод, что у них разный потенциал. В действительности у таких учеников задействованы разные виды активности мозга, причем более важной считается медленная и глубокая. В школах США есть тенденция высоко оценивать быстрое, но поверхностное обучение, результаты которого можно проконтролировать с помощью тестов. Если руководствоваться таким методом оценки, то успеваемость выше у тех, кто быстрее запоминает информацию. Но при этом исследование показывает, что те, кто сталкивается с большим количеством трудностей и обучается медленнее, в долгосрочной перспективе достигают наилучших результатов.
Быстрое обучение вредно еще и тем, что более медлительные ученики сравнивают себя с более успешными. Обычно это проявляется в ощущении неспособности решать поставленные задачи. В школах и колледжах США учащиеся обычно ставят на себе крест, видя, что другие работают быстрее. Нэнси Кушер, заведующая кафедрой математики в школе, работающей по программе некоммерческого частного образовательного фонда «Международный бакалавриат», описывает типичный случай: ученица махнула на себя рукой, видя, что другие осваивают математику быстрее. Начав учиться у Нэнси, Милли заявила, что ненавидит математику, и назвала себя тупицей. Вот записка, которую она написала Нэнси.
Я смотрела на детей, сидевших рядом, которые справлялись с заданием намного быстрее меня. Когда я только-только приступала к решению, они уже заканчивали. Я всегда сравнивала себя с ними и думала: «У меня никогда так не получится».
Милли не одинока в своих переживаниях, и теперь мы знаем, что именно они заставляют мозг хуже работать. Нэнси решила изменить вектор развития Милли и сделала это очень бережно и целенаправленно. Она попросила девочку сосредоточиться на себе, не сравнивать себя с другими и добиться цели: за ближайшие несколько недель разобраться в чем-то одном. Милли сказала, что хотела бы наконец понять, что такое целые числа.
«Отлично, — ответила Нэнси. — Давай договоримся: мы на время отложим все занятия в рамках нашей программы и будем заниматься только целыми числами. И работать станем вместе».
Для начала Нэнси показала Милли ряд визуальных образов, ассоциирующихся с целыми числами, — числовые оси, шкалы термометров и фотографии сумочек Prada. В течение года она находила для Милли и других учеников способы работать более творчески. К концу учебного года Милли очень изменилась и по окончании учебы написала Нэнси письмо.
Уважаемая мисс Кушер, я хочу поблагодарить вас за то, что вы прекрасный учитель. Я не просто считаю вас замечательным человеком — вы еще и по-настоящему отличный учитель. Сперва я сочла ваши видеоролики о людях, которые не могли решать математические задачи, неправдоподобными. Думала, что только я не справляюсь с математикой. До меня не доходило, что с такими мыслями я никогда не смогу хоть немного продвинуться в этом направлении. Вы научили меня не только самому предмету и способам решения математических задач, но и тому, как в целом воспринимать жизнь.
Я творческий человек, математика никогда не была моим коньком. Когда вы стали говорить с нами образами и объяснять, почему мы делаем это, — вместо того чтобы просто показать, как это сделать, — я начала что-то понимать. А если я что-то поняла, то не останавливаюсь на достигнутом. Вы очень помогли мне разобраться во всем этом.
Прошел почти год, и я чувствую, что сильно выросла. Я вообще не думала, что смогу столь многому научиться. Вы всегда говорили: «Милли, просто попробуй», а я думала: «Конечно, попробовать можно, но у меня никогда не получится». Как же я ошибалась! Вы были уверены, что я смогу, и это весь год помогало мне справляться с трудностями. Поэтому говорю вам спасибо!
В письме упомянут важный момент, проясняющий суть вопроса: Нэнси верила в свою ученицу и продолжала подбадривать ее. Не менее важны и другие слова Милли: «Когда вы стали говорить с нами образами и объяснять, почему мы делаем это, — вместо того чтобы просто показать, как это сделать, — я начала что-то понимать. А если я что-то поняла, то не останавливаюсь на достигнутом». Тут Милли уловила суть обучения, о чем мы говорили в предыдущей главе: недостаточно давать ученикам положительную обратную связь — необходимо обеспечить понимание предмета и предоставить возможность успешно справляться с задачами.
Это возвращает нас к многоплановому подходу, когда процесс обучения открытый и творческий, а визуальные представления задач помогают ученикам взглянуть на математические факты под другим углом и справиться с освоением материала. Такой подход куда более эффективен, чем запоминание и зубрежка, на которые ориентировались в прошлом. Но все же во многих областях мы продолжаем поощрять навыки запоминания, хотя известно, что ученики с хорошей памятью не обладают большим потенциалом в отношении математики. Они осваивают предмет, часто совершенно не понимая методов, предложенных учителями. Я встречала многих успешных в математике студентов (даже тех, для кого математика — профилирующий предмет) в лучших университетах, которые сокрушались, что в действительности не поняли ни одной своей работы, написанной за эти годы. Когда механическое заучивание ценится больше, чем глубина понимания, это вредит людям, мыслящим медленно и глубоко, поскольку они теряют интерес к нему. Но это не приносит пользы и тем, кто способен хорошо запоминать, — им бы помог подход к знаниям, дающий глубокое понимание предмета.
Когда Нэнси составила пособия для визуального решения математических задач и объяснила ученикам, почему мы это делаем, а не как это сделать, то Милли впервые справилась с заданием и, сделав это однажды, продолжала двигаться дальше. В результате постепенно избавилась от ложного представления о том, что никогда не сможет успевать по математике.
Нэнси старалась работать так, чтобы все ученики в ее классе и других классах школы приобрели положительный опыт в изучении математики. Среди ее учеников были и те, кто поставил на себе крест, и она делала все возможное, чтобы изменить их представление о себе. Нэнси дала Милли домашнее задание, которое помогло девочке посмотреть на математику с другой стороны. Во время школьных тестов она сидела рядом с Милли и показывала ей, как можно найти решение с помощью визуальных инструментов. До того как девочка попала в класс к Нэнси, по математике ей ставили только D и F. По итогам учебного года Милли получила оценку B. Но более важным оказалось то, что она начала понимать материал и больше не считала себя неспособной к математике.
Нэнси проработала со всеми учителями идеи, которые легли в основу и этой книги, и книги «Математическое мышление», и моих онлайн-уроков. Размышляя о произошедших в школе переменах, она написала:
Я не думала, что когда-нибудь мне повезет увидеть группу учителей, настолько увлеченных работой с детьми и преподаванием математики. И мне не терпится увидеть перемены в их учениках. Это касается не только моего класса или какого-то одного ученика, но и других детей, а также многих учителей, которым пошли на пользу перемены, повлиявшие на их повседневную жизнь.
Удивительная история о том, как благодаря усилиям учителя изменилась не только сама Милли, но и ее взгляды и подход к жизни, выявляет способы, с помощью которых ученики могут преодолеть ограничения и снять их. Чтобы лучше понять эту теорию, мы намерены глубже погрузиться в изучение математики. В помощь нам будут результаты захватывающего исследования, которые вне зависимости от изучаемого предмета содержат важные выводы для учителей и учащихся, а также для родителей и руководителей. Данное исследование позволяет понять принцип работы человеческого мозга и роль гибкости мышления.
Гибкое мышление
Профессора британского Уорикского университета Эдди Грей и Дэвид Толл работали с учениками в возрасте от 7 до 13 лет. Учителя отнесли их к числу слабых, середнячков и сильных. Исследователи давали ученикам арифметические задачи, показывали визуальные решения, а затем анализировали, какими способами школьники получили результат. Так, в примере 7 + 19 числа были представлены визуально (см. рис. 5.2).
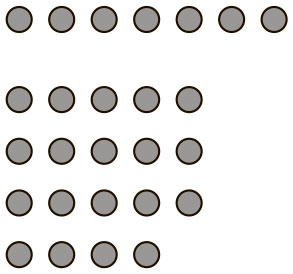
Рис. 5.2. Визуальное представление сложения двух чисел — 7 и 19.
Ученые обнаружили, что разница между сильными и слабыми учениками состояла не в том, что первые знали больше. Сильные школьники решали задачи с помощью так называемого чувства числа — их работа носила гибкий и концептуальный характер. Исследователи выделили два метода подсчета: в рамках метода «считаем всё» дети просто считали, сколько в первом множестве, сколько во втором и потом складывали первое со вторым; метод «продолжение счета» используется, когда заданы два числа (например, 15 и 4). В этом случае сложение осваивается так: сначала дети считают до 15, а затем продолжают счет — 16–17–18–19. Изучая метод продолжения, ученики усваивают понятие суммы. Речь не о методе сложения, а о самой идее. Знание математических фактов проявлялось тогда, когда испытуемые помнили их, а чувство числа — в случаях, когда они гибко оперировали числами, например решали задачу на сложение 7 + 19, упрощая ее и вычисляя сумму 6 + 20. Ниже приведены методы, которыми пользовались сильные и слабые ученики.
Сильные ученики:
30% — знание математических фактов;
9% — метод продолжения счета;
61% — чувство числа.
Слабые ученики:
6% — знание математических фактов;
72% — метод продолжения счета;
22% — метод «считаем всё»;
0% — чувство числа.
Результаты оказались впечатляющими. Сильные ученики мыслили гибко; у 61% из них проявилось чувство числа. Слабые вообще не обращались к чувству числа. Они применяли другие методики счета, например продолжение счета или обратный счет (начиная с какого-то одного числа и считая в обратном порядке), причем придерживались формальных схем даже в тех случаях, когда это не имело смысла. Исследователи высказали важное соображение: слабые ученики, не отличавшиеся гибкостью мышления, изучали другую математику, более сложную. Это проиллюстрировали с помощью задачи на вычитание: 16–13.
Слабые ученики решали ее с помощью обратного счета, то есть выбирали более трудный путь (попробуйте-ка начать с 16 и отсчитать 13 чисел в обратном порядке); при этом вероятность ошибки довольно высока. Сильные ученики действовали гибко, вычитая 3 из 6 и 10 из 10, получали ответ 3. Подобная гибкость в обращении с числами предельно важна, но если учеников обучают слепо заучивать математические факты и применять математические методы без понимания их сути, то они автоматически обращаются к тому, что вызубрили, и никогда не разовьют способность концептуально размышлять о числах и гибко взаимодействовать с ними.
Часто с отстающими учениками начальной школы занимаются дополнительно и отдельно от других, особенно если у них проблемы со счетом, — подход под названием «тренировать и готовить» сами ученики метко переименовали в «тренировать и убивать». Это последнее, что им нужно. Такие ученики не успевают по математике из-за неправильного подхода к обучению, думая, что им необходимо опираться на запоминание. Даже в тех случаях, когда чувство числа принесло бы им больше пользы, они продолжают применять методы счета, основанные на заучивании. Вместо того чтобы заниматься зубрежкой, им необходимо научиться гибко и творчески обращаться с числами. Они должны подходить к числам по-другому — концептуально.
Концептуальное обучение
Что это значит — подходить к числам концептуально? Многим читателям, кому внушали, что нужно запоминать математические методы и факты, это может показаться чужеродной идеей. Грей и Толл разграничили концепции и методы (рис. 5.3).
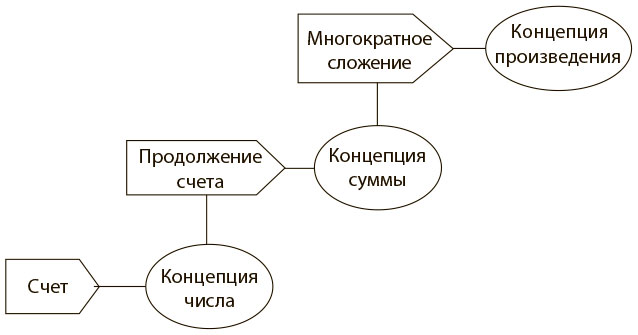
Рис. 5.3. Математические методы и концепции
Мы изучаем такие методы, как счет, чтобы сформировать концепцию числа — представление о нем. Мы осваиваем метод продолжения счета, чтобы воспринять концепцию суммы, а усвоив метод многократного сложения, мы поймем концепцию произведения.
Математика — концептуальный предмет, но многие ученики не видят ее в таком ракурсе. Математика для них — это набор правил или методов, которые нужно запомнить. Как мы уже обсуждали, такой подход становится в итоге серьезной проблемой, и некоторые исследования мозга проливают свет на причины, по которым это происходит.
Когда вы изучаете область, о которой ничего не знаете, она занимает много места в вашем мозге: ведь вам нужно напряженно размышлять, как это работает и как разные концепции соотносятся друг с другом. Но математические понятия, которые вы изучили ранее и хорошо знаете (например, сложение), занимают в мозге небольшое пространство. Вы можете использовать эти знания, даже не задумываясь. Процесс сжатия происходит потому, что головной мозг — крайне сложный орган, контролирующий много разных процессов, и в один момент он может сосредоточиться только на нескольких несжатых концепциях. Те же, которые вы хорошо знаете, сжимаются и архивируются. Уильям Тёрстон, выдающийся математик, получивший Филдсовскую премию, так описывает процесс сжатия.
Математика поразительно легко поддается сжатию: вы можете долго и напряженно трудиться, шаг за шагом прорабатывая один процесс или идею с нескольких точек зрения. Но как только вы по-настоящему поймете нечто и сможете увидеть это как единое целое, скорее всего, произойдет очень сильное ментальное сжатие. Вы можете отправить эту информацию в архив, а при необходимости быстро и полностью восстановить и использовать ее всего лишь за один шаг в рамках другого ментального процесса. Озарение, которым сопровождается такое сжатие, — одна из истинных радостей.
Многие ученики не считают, что математика дарит подлинную радость, — отчасти потому, что в их мозге сжатия не происходит. Мозг способен сжимать только концепции, но не правила и методы. Следовательно, у учеников, которые не мыслят концептуально, а воспринимают математику как список правил, подлежащих запоминанию, сжатия не происходит и их мозг не может упорядочивать концепции и архивировать их, а пытается хранить длинные списки методов и правил. Вместо сжатых концепций их знания больше напоминают лестницу, состоящую из нагромождения заученных методов и, как им кажется, ведущую наверх. Именно поэтому важно воспитать концептуальный подход к математике — основу математического мышления.
Когда я рассказываю учителям и родителям об этом исследовании, они задают вопрос: «Как сделать так, чтобы мои ученики воспринимали информацию концептуально?» Существует много способов научить детей размышлять на концептуальном уровне. Во-первых, важно донести до них причины, почему работают те или иные методы, а не просто предлагать заучивать их. В предыдущей главе мы говорили о том, насколько важно задавать ученикам вопросы об их видении той или иной идеи и убеждать их в том, что это действительно способствует ее концептуальному пониманию.
Еще один концептуальный подход к преподаванию и изучению математики, названный «Беседы о числах», был задуман преподавателями Рут Паркер и Кэти Ричардсон и разработан Кэти Хамфриз и Шерри Пэрриш. Метод состоит в обсуждении чисел и позволяет ученикам младших и средних классов развивать чувство числа и понимать гибкую и концептуальную природу математики. В ходе обсуждений ученикам предлагают совершить вычисления в уме, не используя бумагу и ручку. Затем учителя собирают информацию о том, какие методы счета использовали ученики.
Обучая других проводить беседы о числах, я, помимо прочего, рекомендую применять визуальные решения, чтобы активировать разные нейронные связи в мозге. Чтобы понять это, попробуйте вычислить в уме, сколько будет 18 × 5, до того как вы прочитаете или подсмотрите пути решения.
На рис. 5.4 приведены шесть разных способов вычисления 18 × 5 (на самом деле их больше) с визуальными решениями.
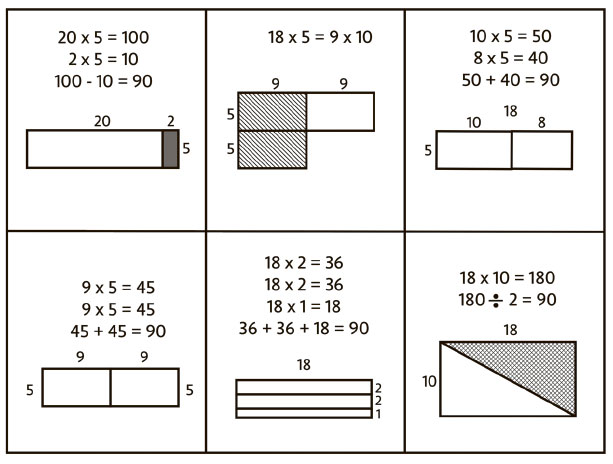
Рис. 5.4. Шесть визуальных решений задачи на умножение
Можно обозначить все проблемы с числами и решать их по-разному, разбивая числа на суммы или произведения и приводя к более «удобным» для счета числам, например 20, 10, 5 или 100. Это упрощает вычисления и способствует гибкости в обращении с числами, лежащей в основе чувства числа. Ученики любят рассказывать о своих стратегиях; как правило, они увлеченно и с интересом анализируют разные методы, используемые при решении задач. Они осваивают ментальную математику, у них появляется возможность запомнить факты, а также формируется концептуальное понимание чисел и арифметических свойств, что крайне важно для успешного изучения алгебры и других разделов математики.
Когда я продемонстрировала разные подходы к решению одной задачи, многие были удивлены и испытали чувство освобождения.
Однажды меня пригласили на встречу с удивительным человеком — профессором Стэнфордского университета Себастьяном Труном и его командой в Udacity, занимающейся дистанционным образованием. Трун руководил разработкой беспилотных автомобилей и был одним из первых создателей открытых онлайн-курсов (Massive Open Online Courses, MOOCs). В настоящее время он разрабатывает летающие автомобили. Я взяла у него интервью для своего первого онлайн-курса, адресованного учителям, чтобы распространить его идеи о математике и преподавании.
Себастьян пригласил меня в Udacity пообщаться с его командой. Тогда мы и познакомились. В тот день я сидела в многолюдной комнате вместе с инженерами. Те, кто втиснулся в небольшое помещение, сидели вокруг стола, остальные расположились на полу вдоль стен. Себастьян представил меня собравшимся и тут же начал забрасывать вопросами о правильных подходах к изучению математики. А я спросила присутствующих, не хотят ли они все вместе решить математическую задачу. Они охотно согласились. Я попросила их найти произведение 18 × 5, затем собрала методы счета, разыграв мини-версию бесед о числах. В тот день для решения примера было использовано шесть разных методов, и я нарисовала их на столе, вокруг которого мы сидели. Вся группа была настолько поражена, что некоторые поспешили на улицу и стали предлагать прохожим посчитать, сколько будет 18 × 5. Впоследствии они записали небольшой онлайн-курс по решению этого примера и изготовили футболки с надписью «18 × 5», которые носили в Udacity.
Я поделилась этим подходом с другим потрясающим лидером в IT-области Люком Бартелетом, который возглавлял разработку игр SimCity и одновременно занимал должность исполнительного директора Wolfram Alpha, сайта с данными, вычисляемыми онлайн. Он также был воодушевлен примером и начал предлагать каждому решить его.
Конечно, 18 × 5 не единственная задача, которую можно решить множеством способов. Однако самые разные люди, прекрасные математики, испытали чувство освобождения, осознав, что существует множество методов решения задачи.
Почему люди так удивляются многоплановому творческому подходу к математике? Одна женщина, которой продемонстрировали решение примера 18 × 5, была потрясена. Она сказала: «Не то чтобы я не знала, что все это можно проделывать с числами, но я скорее думала, что так нельзя».
Учитель из Англии связал свой опыт с «Беседами о числах». Он попробовал вести подобные дискуссии среди своих лучших учеников и начал с задачи 18 × 5. Школьники охотно предлагали разные способы решения, обсуждение получилось живым и интересным. Затем он задал тот же вопрос группе неуспевающих — ответом было молчание. Ученики могли вычислить результат с помощью известного им алгоритма, но других подходов к решению не знали. Учитель предложил подумать о том, как можно решить эту задачу по-другому, например найти произведение 20 × 5. Класс очень удивился: «Но, сэр, мы думали, что так делать нельзя». Сильные ученики усвоили гибкий подход к числам, а слабые не смогли, полагая, что так обращаться с числами непозволительно.
Этот случай свидетельствует об ущербе, нанесенном математическому образованию: люди думают, что гибко обращаться с числами нельзя, а математика состоит из следования правилам и схемам. Неудивительно, что очень многие теряют интерес к предмету. Я часто отмечала эту проблему. Она типична для всех учеников и представителей всех национальностей, но, похоже, особенно характерна для неуспевающих, как следует из приведенного примера и исследования Грея и Толла.
Исключительно эффективный математический навык — упрощать. Когда мы ищем решение сложной задачи, используя меньшие числа, то присущие ей закономерности часто становятся более понятными и осязаемыми. К примеру, рассмотрим изящное доказательство, известное как доказательство Гаусса. Это одна из прекрасных математических закономерностей, которые полезно знать каждому учителю или родителю независимо от того, увлекаются их дети математикой или нет.
Карл Гаусс был немецким математиком, жившим в XIX веке. Я не знаю, насколько правдива часто упоминаемая история про его детские годы, но она замечательная! Когда Карл учился в начальной школе, преподаватель понял, что ему необходимо давать сложные задачи, и, чтобы занять его на долгое время, попросил сосчитать сумму чисел от 1 до 100. Но маленький Карл заметил одну любопытную закономерность и понял, что необязательно складывать все числа, ведь сумма пар чисел, равноудаленных от концов, одинакова: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101 … 50 + 51 = 101 и так далее, и что таких пар ровно 50. Результат был получен мгновенно: 50 × 101 = 5050 (рис. 5.5).
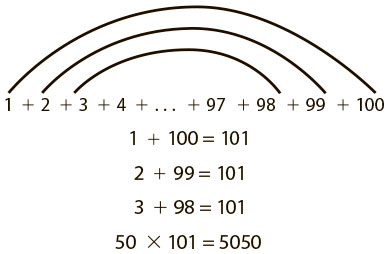
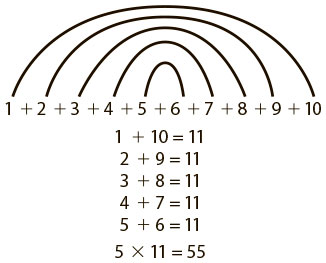
Рис. 5.5. Способ вычисления суммы целых чисел от 1 до 100, примененный Карлом Гауссом, и пример с вычислением суммы целых чисел от 1 до 10
Чтобы понять закономерности в доказательстве Гаусса, полезно рассмотреть пример с меньшим количеством чисел — от 1 до 10. Так мы поймем, почему сложение пары, где одно число на единицу больше, а другое на единицу меньше чисел в предыдущей паре, дает в сумме одно и то же число. Если вам захочется испытать себя и не упустить возможность для развития мозга, рекомендую подумать, как метод Гаусса работает на примере последовательности, состоящей из нечетного количества целых чисел.
Рассмотрение примера с последовательностью чисел от 1 до 10 — по сути, математическая операция, но когда я объясняла это ученикам, то столкнулась с сопротивлением слабых школьников. Их учили, что математика состоит из набора правил, которым нужно четко следовать. Им совершенно чужда мысль о том, что можно не отвечать на поставленный вопрос, а задать другой, изменить первоначальную задачу; они считают, что тем самым нарушат выученные правила.
Мне кажется, в жизни крайне важно научиться играть с числами и рассматривать математику как предмет, к которому стоит относиться открыто и многопланово. Я говорю это не ради красного словца, а потому что знаю: когда люди иначе рассматривают математику, они так же по-другому видят и собственный потенциал, а это меняет их жизнь и дает возможность пережить опыт, который нельзя получить иным образом. Такое восприятие позволяет им не только преуспеть в математике и STEM-дисциплинах в школе и за ее пределами; оно развивает умение разбираться в количественных показателях, помогает освоить профессии, связанные с финансами, статистикой и другими сферами жизни, немыслимыми без математики.
Если учителя преподают математику как открытый и концептуальный предмет, освоение которого не завязано на временных рамках, это невероятно раскрепощает мышление. Нина Судник, учительница четвертого класса из Огайо, рассказала об одном ученике, испытавшем чувство освобождения после того, как он нашел концептуальное решение математической задачи. Молодую женщину очень удивляло то, как мало знали ее ученики, хотя они изучали математику уже пятый год. Она попыталась понять причины и в конце концов нашла одну из моих предыдущих книг — «При чем тут математика?» (What’s Math Got to Do with It?), которая произвела на нее большое впечатление.
Я читала эту книгу, и если бы я показала ее вам, вы бы увидели, что почти каждое предложение было подчеркнуто. Мой мозг взрывался от разных идей — впрочем, они всегда меня одолевали, только выразить их я не могла. Я не понимала, почему эти ученики испытывают такие трудности.
После летних каникул Нина вернулась в школу и изменила методы преподавания. В конце первого года 64% ее учеников знали предмет на базовом уровне. На следующий год эта цифра увеличилась до 99%.
Нина также пересмотрела принципы ежедневной и еженедельной проверки успеваемости. Теперь она не возвращала ученикам тесты с плюсами и минусами, что служило им фиксированным сигналом об их достижениях, а писала комментарии к работам, указывая на то, что учащиеся поняли, а что только начинают усваивать. Получив свои работы в первый раз, они искали плюсы и минусы, но ни одного не нашли. Нина объяснила, что теперь она рассматривает результаты тестов как показатель того, в какой точке находится ученик на воображаемой шкале понимания предмета.
Кроме того, Нина давала ученикам математические задачи, требующие гибкого и концептуального подхода. Одну из таких задач она взяла из нашего курса «Неделя вдохновляющей математики» (Week of Inspirational Math), где собраны открытые и творческие задачи, которые мы каждый год публикуем на ресурсе Youcubed. Это нерешенная задача из истории математики, которая называется гипотезой Коллатца. Мы представили ее следующим образом.
- Возьмите любое целое число больше нуля.
- Если число четное, поделите его на 2 (уменьшите вдвое).
- Если число нечетное, умножьте его на 3 и прибавьте 1.
- Продолжайте данные операции с полученными числами, пока последовательность не закончится.
- Выберите другое число и создайте аналогичную последовательность. Как вы думаете, что произойдет?
До сих пор никому не удалось найти последовательность чисел, которая не заканчивается числом 1, и никто не смог доказать, почему это так. Данная задача также известна как последовательность чисел-градин, поскольку полученные числа образуют график, похожий на траекторию движения градин в атмосфере, — вверх и снова вниз (рис. 5.6).
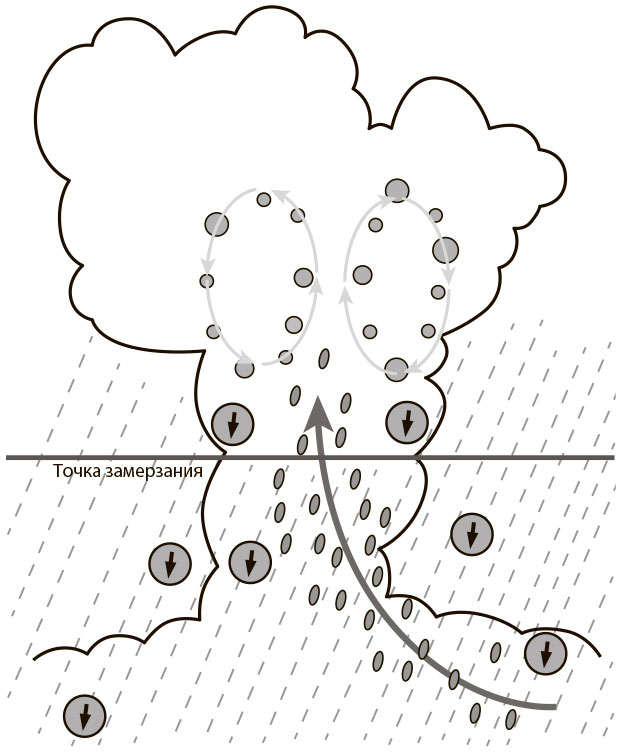
Рис. 5.6. Формирование града
Несмотря на то что данную проблему никто не смог решить, мы посчитали, что она подходит для третьеклассников и учеников постарше. Многие учителя задавали ее своим ученикам, побуждая их быть первыми, кто найдет последовательность, которая не заканчивается единицей, — безусловно, ученикам это нравилось.
Ветер выталкивает капли дождя выше точки замерзания, где они начинают вращаться, замерзают и увеличиваются в размерах, пока не станут достаточно тяжелыми и не начнут выпадать на землю в виде града.

Рис. 5.7. Визуальное отображение числовых закономерностей
Рис. 5.8. Количество шагов, за которое последовательность приходит к единице
Одна из учениц Нины, Джоди, в течение года по состоянию здоровья часто пропускала занятия и не могла выполнять домашнюю работу. Она никогда не любила математику, но была очарована задачей о числах-градинах. Однажды Нина заметила, что карманы Джоди, вышедшей на прогулку, набиты небольшими листками бумаги. Несколько недель карманы все увеличивались, пока листки не начали выпадать.
Наконец Нина спросила у нее, что это такое. Джоди запустила руку в карман и вручила Нине листки с каракулями, где она пыталась изобразить разные графики последовательностей. Неделями девочка старательно работала над гипотезой Коллатца, проверяя одну последовательность за другой. Нина задумалась и поделилась своими мыслями со мной.
Джо, она знает эту последовательность и чертовски этим гордится. Я сказала ей: «Мне неважно, будешь ли ты весь год выполнять домашние задания. (Усмехается.) Просто продолжай работать над последовательностью чисел-градин».
Многие ребята говорили: «Ничего себе! Каждый раз, когда мы доходим до 16, последовательность повторяется». Я им: «Правда?»
Джоди чувствовала, что достигла успеха, — возможно, первый раз за все время изучения математики, так что спасибо тебе за это.
То, насколько вредит нашей системе образования упор на запоминание в ущерб концептуальному обучению, было прямо показано в недавнем тесте, проведенном командой Международной программы по оценке образовательных достижений учащихся (Programme for International Student Assessment, PISA). Данную программу курирует Организация экономического сотрудничества и развития (Organisation for Economic Co-operation and Development, OECD), расположенная в Париже. Программа представляет собой тест на проверку грамотности и умение применять полученные знания на практике; он проводится по всему миру каждые три года среди подростков 15 лет. Команда PISA пригласила меня в Париж, чтобы помочь им провести тест.
Как только я расположилась за столом в их офисе, мне сразу задали вопрос: «Что у американцев не так с числом π?» Они имели в виду тот факт, что американские ученики отвратительно справлялись со всеми задачами, связанными с числом π (отношение длины окружности к ее диаметру, иррациональное число, которое начинается с 3,14), — их показатели были чуть ли не худшими в мире. На этот вопрос у меня был ответ.
Переехав из Великобритании в США, я отмечала кое-что любопытное в изучении числа π. В США детей учат запоминать как можно больше цифр после запятой. Число π обычно сокращается до 3,14, но после запятой эта последовательность уходит в бесконечность. Это наводит американских школьников на мысль, будто число π «длится целую вечность», что заслоняет его реальное значение как отношение длины окружности к ее диаметру. На самом деле выраженное этим числом соотношение — динамичное и захватывающее, потому что размер окружности не имеет значения, а отношение длины окружности к ее диаметру всегда одинаковое.
Не так давно я попросила учителей задать ученикам вопрос, что означает число π, и посмотреть, что будет. Конечно же, все назвали его очень длинным, но никто не упомянул про отношение длины окружности к ее диаметру. Неудивительно, что в ходе теста PISA ученики плохо справлялись со всеми задачами, где фигурировала окружность. Нет ничего плохого в том, чтобы поиграть с числом π и позволить ученикам запоминать цифры после запятой (или съесть π-рожок, что тоже неплохо). Но все подобные действия необходимо сопровождать более глубоким изучением окружности и отношения ее длины к диаметру.
В 2012 году команда PISA исследовала не только успеваемость учеников, но и их подход к учебе. В дополнение к математическим задачам исследователи выдали школьникам анкету, где те должны были описать, как они учатся. Полученные ответы разделили на три категории. Подход, основанный на запоминании, использовали те ученики, которые старались заучивать наизусть все, что им давали. При реляционном подходе ученики пытались соотнести новые идеи с уже известными им. И наконец, подход, основанный на самодисциплине, предполагал, что ученики сами оценивали то, что знали, и осваивали то, что им нужно.
В любой стране самыми отстающими были ученики, усваивающие новое через зазубривание, а страны, где таких учеников было много, — и США в их числе — в целом имели самые низкие показатели. Например, французские и японские школьники, которые совмещали реляционный подход и самодисциплину, более чем на год опережали тех, кто налегал на зубрежку. Исследование показало, что это не приводит к высоким результатам, в отличие от размышлений о концепциях и их взаимосвязях.
Как показывает этот тест, преподавание математики в США находится в кризисе. Математика — прекрасный предмет, полный логических взаимосвязей, ее следует изучать концептуально и творчески. Однако в школах, где математику рассматривают как набор правил для запоминания, и ценятся те, кто может быстро выдать все, что успел запомнить; мыслящие медленно и глубоко дети теряют интерес к предмету. Даже сильные ученики многое недополучают от уроков математики.
Людям, иначе воспринимающим знания, открываются двери в другой мир. Они узнают о концепциях, в сжатом виде хранящихся в глубинах мозга, и закладывают прочную основу для понимания предмета. Они способны превратить математическое мышление в один из своих навыков и использовать его не только на уроках математики, но и на всех других занятиях. В нынешней школьной системе лишь немногие сильные ученики умеют мыслить гибко — именно они становятся первооткрывателями в самых разных областях.
Марк Петри и Нина Судник, о которых упоминалось выше, были хорошими учителями еще до знакомства с идеями, изложенными в этой книге, в их классах было много сильных учеников. Однако теперь, когда они подходят к математике концептуально и творчески и учат тому, как важно мыслить глубоко, процент успевающих в их классах существенно вырос.
Как сказал Боб Мозес, один из наиболее влиятельных лидеров движения за гражданские права в 1960-х годах, развивать понимание математики — одно из прав гражданина. Математика открывает двери и в учебные заведения, и в жизнь.
Многие убеждены, что высокого профессионализма и понимания предмета можно достичь с помощью большего интеллектуального багажа, и считают, что учеба сводится к накоплению знаний. Но исследования свидетельствуют о том, что успешные люди используют гибкое мышление. В действительности же творческое и гибкое мышление — весьма полезный и ценный инструмент в работе — подавляется большим количеством знаний. Вот почему, когда задача требует творческого решения, предполагающего понимание закономерностей и обнаружение неожиданных логических связей, хорошо подготовленные специалисты часто терпят фиаско — в отличие от людей со стороны, сумевших найти иной подход.
Адам Грант в книге «Оригиналы. Как нонконформисты двигают мир вперед» утверждает, что долгое время мы выделяли учеников, действующих по правилам и хорошо запоминающих материал. Он отмечает, что в США учащиеся, которых часто считают вундеркиндами, — а именно те, кто «уже в два года умеют читать, в четыре года играют Баха, в шесть овладевают дифференциальными уравнениями, а к восьми годам бегло говорят на семи языках», — редко меняют мир. Наиболее влиятельные люди, биографии которых изучают школьники, в детстве редко считались одаренными или гениями. Напротив, лучшие ученики в школе часто «находят своим исключительным способностям самое обычное применение, хорошо справляются со своей работой, не ставя под сомнение существующий порядок вещей и не нарушая всеобщее спокойствие». Грант делает вывод: «Хотя мы привыкли думать, что Земля вращается именно благодаря добросовестным труженикам, на самом деле мы вместе с ними бежим, словно белка в колесе, не продвигаясь вперед. Вундеркиндам мешает их нацеленность на успех». Те гении, кто действительно меняют мир, мыслят гибко, выбирают скорее нестандартные подходы и не ограничены шаблонами.
Многие люди осознают ценность гибкого и творческого мышления, но не связывают его с математикой: они рассматривают ее лишь как область, где нужно следовать выученным правилам и соответствовать требованиям. Но когда мы соединяем математику с креативностью, гибкостью и мышлением роста, происходит чудесное освобождение. Каждому стоит пережить подобный опыт — после него редко кто оглядывается назад.
Преимущества глубокого и гибкого мышления распространяются на все сферы жизни. Мы не знаем, какие проблемы людям придется решать в будущем, — скорее всего, мы даже приблизительно не можем себе их представить. Маловероятно, что заполнение мозга информацией, которую мы можем быстро воспроизвести, поможет их решению. Гораздо полезнее приучать себя мыслить глубоко, гибко и творчески. Новаторы, чей мозг тщательно исследовали, обладали более гибким, чем у обычных людей, мышлением. Они научились решать проблемы разными способами и не полагаться только на память. Скорость и неизменные методы решения работают до определенного предела. Необходимо бросить вызов идеям о преимуществах скорости и запоминания в сфере образования и других областях и сосредоточиться на гибком и творческом обучении. Это поможет нам высвободить потенциальные возможности для обучения — как у самих себя, так и у других.

