Глава 4
Коннективность мозга
Очень важно идти по жизни, руководствуясь мышлением роста, с пониманием, что по ту сторону проблемы нас ждет успех и нет ничего недостижимого. Люди постепенно осознают ценность такого мышления. Однако есть один фактор жизни без границ, пока плохо изученный, но крайне важный для сохранения открытыми всех жизненных путей. Речь идет о новом, динамичном способе взаимодействия с новыми идеями как в области научного знания, с которой вы соприкасаетесь в процессе обучения, так и в других жизненных ситуациях.
Ключевой навык обучения № 4
Нейронные связи и процесс обучения оптимизируются при многоплановом подходе к новым идеям.
Мы уделили много внимания мышлению и неизменной вере в себя, но когда вопрос касается обучения, одного лишь призыва к студентам развивать мышление роста уже недостаточно для снятия противоречивых установок, существующих в нашей культуре. Кэрол Дуэк полагает, что информацию о смене одного типа мышления на другой необходимо сопровождать иным подходом к преподаванию, который поощряет учиться по-новому. Она уверяет, что не спит ночами, когда слышит, как студентам велят усердно заниматься — ведь успех придет по итогам упорного труда, но при этом не предлагают инструментов для более эффективной учебы. По словам Кэрол, «усилия — это ключ к успеваемости, но он не единственный. Учащиеся должны пытаться применять разные стратегии и, заходя в тупик, искать помощи у других».
Известный психолог, лектор и независимый исследователь в области образования Альфи Кон критикует людей, ратующих за смену типа мышления. По его мнению, нечестно призывать студентов меняться и работать упорнее, не меняя при этом систему. Я с ним полностью согласна и за долгие годы уяснила одну важную вещь: чтобы развить мышление роста, учителя тоже должны использовать в преподавании установку на рост, создавать среду, поощряющую поиск разных путей для решения задачи и разных способов для обучения, чтобы ученики увидели в этом потенциал для собственного развития. А если материал преподносится в виде фиксированного набора вопросов с одним правильным ответом и единственным способом его получения, мышление невозможно переориентировать на рост.
Как же учителям, родителям и руководителям определить методы, расширяющие и поддерживающие позитивный посыл относительно роста и обучения? Решение — в многоплановом подходе к обучению и преподаванию. Этот подход — результат последних достижений нейробиологии, к которым пришли ученые из Стэнфорда и других университетов, а также множества экспериментов, проведенных среди учеников средних и старших классов.
В Стэнфорде я сотрудничала с нейробиологами, в частности с группой исследователей под руководством Вино Менона с медицинского факультета. Ланг Чен, нейробиолог из лаборатории Менона, регулярно выступает на канале Youcubed. Стэнфордские ученые изучают активность нейронных сетей, фокусируясь на способах работы мозга — например, при решении математических задач. Ученые обнаружили, что даже при решении простого арифметического примера задействуются пять участков мозга, два из которых — нейронные пути зрительной коры. По дорсальному зрительному пути передается визуальная информация о количестве объектов (рис. 4.1).
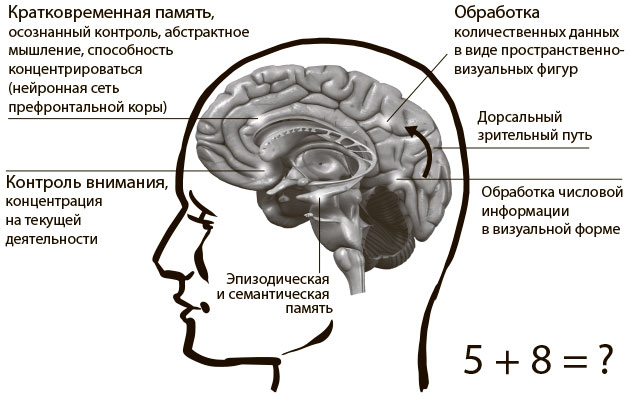
Рис. 4.1. Нейронная сеть для освоения ментальной математики
Вместе с другими нейробиологами они обнаружили, что связность разных участков мозга ускоряет процесс обучения и улучшает результаты. В 2013 году Парк Джун Ку и Элизабет Брэннон рассказали об исследовании, в ходе которого обнаружили, что при работе с символами (в частности, с числами) и с визуальной и пространственной информацией в мозге задействуются разные отделы. Также они выяснили, что эффективность обучения возрастает, если два этих участка взаимодействуют друг с другом. Мы можем воспринимать математические концепты как через числа, так и через слова, визуальные образы, модели, алгоритмы, таблицы и графики, через движение и касание, а также другие формы. Если мы применяем два или более способов усвоения материала, то тем самым максимизируем эффект обучения и участки мозга, отвечающие за каждый из этих способов, «общаются» между собой. Об этих открытиях вплоть до недавнего времени было мало известно, их результаты практически не применялись в преподавании.
Ученые, занимающиеся взаимодействием разных участков мозга, для анализа использовали математические примеры, но их выводы можно экстраполировать на все области знания. Обучение новому требует активации нескольких нейронных путей — например отвечающих за внимание, память, размышление, коммуникацию, визуализацию. Подходя к новому знанию многопланово, мы стимулируем все эти пути, укрепляем мозг и делаем процесс обучения максимально эффективным.
Удивительные факты о пальцах
Новые подробности о том, как мозг обрабатывает математические данные, порой удивительны. Так, в рамках одного исследования удалось доказать значение пальцев для усвоения математики. Илария Бертелетти и Джеймс Бут проанализировали отдельный участок мозга — соматосенсорную систему, отвечающую за обработку информации от рецепторов, расположенных в том числе на пальцах. Ученые обнаружили, что когда подросткам 8–13 лет дают сложные задачи на вычитание, соматосенсорная система активизируется, даже если школьники не задействуют пальцы. Примечательно, что у нас в голове возникает образ пальцев, даже когда мы не используем их при вычислениях. Этот участок мозга, согласно тому же исследованию, в значительной степени вовлечен и в решение более сложных примеров, включающих большие числа и подразумевающих несколько операций.
Нейробиологи установили связь моторики с математическим мышлением, особо выделив значимость «пальцевого восприятия». Проверить его можно следующим образом. Спрячьте одну ладонь под книгу или под стол и попросите кого-нибудь дотронуться до кончиков ваших пальцев. Люди с хорошим восприятием легко определят, какого именно пальца коснулись. Более сложный тест предполагает прикосновение в двух разных точках — на кончике пальца и второй фаланге. Вот несколько интересных фактов.
- Уровень пальцевого восприятия у студентов колледжей позволяет спрогнозировать результаты тестов на счет.
- Пальцевое восприятие в первом классе надежно предсказывает успеваемость по математике во втором классе.
- Долговременные наблюдения подтвердили, что высокой успеваемостью по математике музыканты, по всей видимости, обязаны хорошо развитому пальцевому восприятию.
Нейробиологи установили, насколько важно для маленьких детей развивать мелкую моторику: эта способность выполнять мелкие и точные движения проявляется при счете на пальцах. Однако многие учителя категорически против обучения счету таким способом, а сами учащиеся часто считают его ребячеством. Я пыталась изменить эту практику, рассказывая о достижениях нейробиологов в СМИ, соцсетях и журналах. Кроме того, я участвую в деятельности междисциплинарной группы нейробиологов, инженеров и педагогов, работающей над созданием небольших роботов, развивающих восприимчивость пальцев у маленьких детей. Новые открытия указывают на необходимость иного подхода к преподаванию — более физически ориентированного, многопланового и креативного, нежели те, что использовались раньше и применяются сейчас.
А как же новаторы?
В процессе исследования способов, с помощью которых люди приходят к высоким результатам, ученые выявили новые интересные данные о взаимодействии разных участков мозга. Некоторые выдающиеся таланты, в частности Моцарт, Кюри и Эйнштейн, часто считаются гениями по умолчанию. Андерс Эрикссон, Дэниел Койл и другие психологи показали, что великие достижения этих удивительных людей — следствие упорного, многолетнего, самоотверженного труда.
Андерс Эрикссон исходит из предположения, будто Моцарт родился с особым даром, что впоследствии якобы способствовало созданию гениальных произведений, и анализирует его деятельность в раннем возрасте. Андерс отмечает, что Моцарт, по словам современников, обладал идеальным слухом. Это классический пример врожденного дара, поскольку идеальный слух в норме встречается у одного из 10 тысяч человек. Однако внимательное изучение биографии Моцарта показывает, что он активно выполнял упражнения для развития идеального слуха уже с трех лет.
Японский психолог Аяко Сакакибара обнародовал результаты исследования, в ходе которого 24 учащихся тренировали идеальный слух. Для определения аккордов дети, услышав звуки, брали разноцветные флажки и делали это до тех пор, пока не смогли правильно назвать каждый аккорд. В ходе эксперимента каждый участник развил идеальный слух. Это хороший пример того, что качество, воспринимаемое многими как дар, на самом деле развивается в ходе особого метода обучения, который задействует множество нейронных путей, в данном случае соединивших звуки и визуальные образы.
Альберт Эйнштейн, человек, которого, возможно, чаще всего называют гением, исключительно эффективно использовал ошибки для обучения. Вот несколько моих любимых цитат.
- Человек, который никогда не совершал ошибок, никогда не пробовал ничего нового.
- Все это так не потому, что я такой умный. Это все из-за того, что я долго не сдаюсь при решении задачи.
- У меня нет особого таланта. Я просто страсть как любопытен.
- В центре проблемы лежит возможность.
По этим и другим цитатам Эйнштейна очевидно, что он обладал мышлением роста, хотя такого концепта при его жизни еще не существовало. Эйнштейн говорил о принятии трудностей, длительной работе над сложными задачами, любопытстве, совершении ошибок и отказе от таких фиксированных понятий, как талант и одаренность. Он также визуализировал идеи и часто говорил, что мыслит всегда визуально, а потом с трудом преобразует свои зрительные образы в слова и символы.
Эйнштейн оказал масштабное воздействие на науку, и неудивительно, что его считают гением. У него не было инструментов и технологий, которыми мы располагаем сегодня, но одной силой мысли он предсказал, что черные дыры, вращаясь рядом друг с другом, создают гравитационную «рябь» (складки) в искривленном пространстве-времени. Потребовались 100 лет и, как писали в National Geographic, «огромная вычислительная мощность», чтобы доказать его правоту. И при всех своих выдающихся достижениях Эйнштейн всегда подчеркивал, что это итог упорной тяжелой работы и визуального подхода к знанию, а не следствие дара или особого таланта. Эйнштейн использовал принцип безграничности в обучении и жизни, и это помогло ему во всех областях.
В недавней статье в журнале National Geographic «Что делает гения?» рассказывается об изучении мозга Эйнштейна, изображения которого содержатся на 46 микрослайдах и хранятся в музее в Филадельфии. Исследователи пытались обнаружить какие-либо особенности. Многие посетители разглядывают мозг Эйнштейна и не видят в нем ничего примечательного. Группа ученых во главе со Скоттом Барри Кауфманом из Института воображения (Imagination Institute) выбрала другой подход, изучая мозг живых людей, развивших невероятные способности. Главным отличием мозга новаторов оказалось наличие большего количества активных связей между разными участками мозга, большего количества связей между полушариями и, соответственно, большей гибкости мышления по сравнению с обычными людьми. Высокая коннективность — отличительная черта мозга новаторов — не считается врожденным свойством, она развивается в процессе обучения.
Как развивать коннективность мозга
На уроках математики школьникам часто выдают листы с набором практически одинаковых примеров, которые надо решить. Когда это происходит, они упускают возможность укрепить нейронные связи. Значительно полезнее выбрать три-четыре примера и решить их разными способами. Так, любую математическую задачу можно свести к следующим вопросам.
- Можете ли вы решить этот пример с помощью чисел?
- Можете ли вы решить пример визуально, закодировав каждое число своим цветом?
- Можете ли вы написать рассказ с этой задачей?
- Можете ли вы отобразить идею по-другому — через набросок, дудл, физический объект, форму или движение?
Один из способов развития многопланового подхода — использование «бриллиантовой бумаги», по определению режиссера канала Youcubed, моей коллеги и подруги Кэти Уильямс. Идея состоит в том, чтобы сложить лист бумаги следующим образом (рис. 4.2).
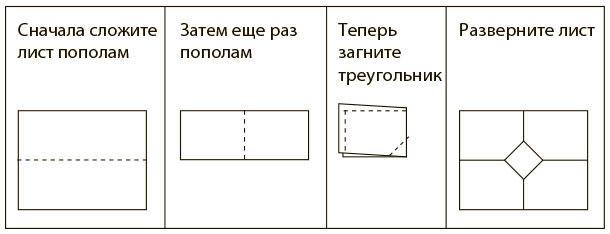
Рис. 4.2. Метод «бриллиантовой бумаги» в рамках многопланового подхода к обучению
Мы призываем учителей помещать пример в центр листа, а чистые четыре четверти использовать для демонстрации разных способов решения (исходя из типа мышления). Так, вместо решения задач на деление по списку (верхняя часть листа) мы предлагаем использовать «бриллиантовый лист» для одного примера 50 ÷ 8 (см. рис. 4.3).
От такого*
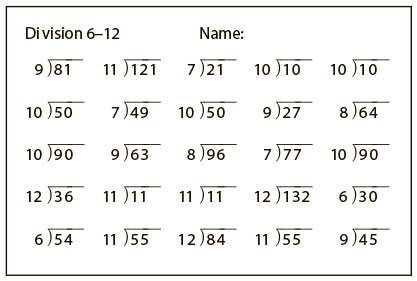
К такому
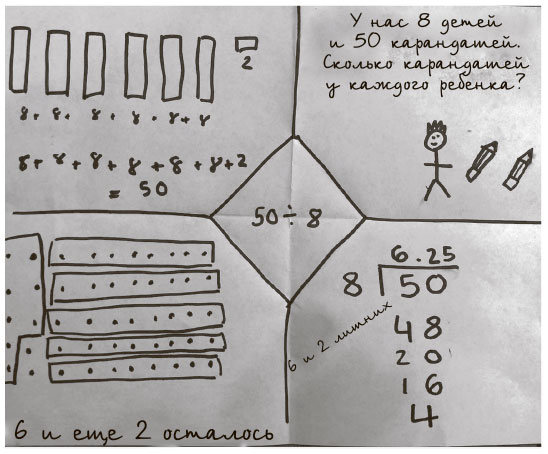
Рис. 4.3. Пример использования «бриллиантового листа» для решения задачи разными способами
* В российских школах детей учат делению в столбик, разбивая вычисления с многозначными числами на несколько шагов (справа). Американские школьники учатся такому же способу деления, однако записывают эти операции иначе (слева). Прим. ред.
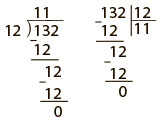
Решение задачи разными способами важно в любой области знаний. На уроках литературы школьники проходят «Ромео и Джульетту», анализируя разные сюжетные линии. Можно также выбрать одну тему (скажем, тему семьи) и рассмотреть ее с нескольких сторон: подобрать соответствующее видео с музыкой, снять собственное видео, нарисовать комикс, сделать презентацию в PowerPoint или изготовить скульптуру. Мультимодальное мышление создает возможность для формирования и укрепления новых связей в мозге. Согласно наблюдениям нейробиологов, гибкий адаптивный мозг — следствие синхронной работы нескольких его участков. Взаимодействие между ними происходит тогда, когда мы приходим к знанию различными тропами, представляем концепции в разных формах и видах.
Многоплановый подход можно использовать для преподавания любых предметов, что увеличит вовлеченность и повысит успеваемость. Во многих дисциплинах, прежде всего гуманитарных, уже оценили многоаспектную разработку темы, когда учащимся предлагают давать собственные интерпретации прочитанных текстов и применяют групповые дискуссии, дебаты и ролевые игры. Разумеется, количество измерений можно увеличить, но в любом случае подход к преподаванию этих дисциплин сегодня уже не столь узок. По моему опыту, изменения требуются прежде всего в математике, естественных науках и преподавании языков. Многоплановый подход к содержанию урока — идеальный метод обучения любой дисциплине.
Недавно я познакомилась с преподавателем-новатором, обучающим иностранному языку. Он ставит учащихся в круг и предлагает им представить себя знаменитостями, говорящими на том или ином языке. Когда ученика похлопывают по плечу, он рассказывает об ощущениях своего персонажа в данный момент. Такая простая и креативная идея моментально выводит урок за пределы чтения и перевода слов и фраз. Учащиеся привыкают выражать и интерпретировать мысли другого человека.
Мне никогда не понять узкого подхода к преподаванию естественных наук — в виде перечня правил и фактов. Это прямой путь привить отвращение к предмету, хотя в его основе лежат открытие, эксперимент, многопричинность и многофакторность. Мы должны вовлечь учащихся в чудо, каким является физика, равно как и в чудо математики. Это значительно важнее заучивания законов термодинамики, которые всегда можно подсмотреть в учебнике или интернете.
Один из самых удачных подходов к изучению естественных наук демонстрирует Джон Лоуз, книгу которого — «Дневник художника-натуралиста» — я очень люблю. На первый взгляд, это книга о природе, но Лоуз рассказывает о самых разных принципах научного знания и, что самое главное, использует несколько методов исследования своих объектов. Его идеи по изучению природы можно перенести на самые разные научные области. Он предлагает исследовать события, собирая данные, обнаруживая закономерности, исключения и изменения; фиксируя происходящее, рисуя карты, строя графики и диаграммы. Затем Джон демонстрирует несколько способов глубокого анализа данных, включая создание текстов, построение диаграмм, запись звуков, составление списков, подсчет и измерения, использование инструментов для обработки данных, а также комплектуя «набор любознайки», включающий лупу, компас и бинокль.
Лоуз исповедует многоплановый подход к изучению естественных наук, что подразумевает знакомство с основными теориями и концепциями через разные типы источников — данные, закономерности, карты, тексты и диаграммы. Когда ученик постигает предмет в разных форматах, у него возникают новые нейронные пути, которые позволяют разным, прежде изолированным участкам мозга взаимодействовать между собой, создавая тот тип связей, который исследователи обнаруживают в мозге новаторов.
Работая с учителями, я часто получаю очень теплые отклики на призыв сделать преподавание многоплановым. Но вслед за этим следует вопрос: «Как же мы сможем так преподавать, если нам в обязательном порядке необходимо пройти с учениками все темы в рекомендованных учебниках?» Многие педагоги работают с определенной (жестко регламентированной) учебной литературой, авторы которой не имеют ни малейшего представления о ценности многопланового обучения.
Когда мне задают этот вопрос, я предлагаю выбрать из списка примеров/заданий три-четыре лучших и затем вовлечь учеников в иную работу — так, как описано выше. Это под силу любому педагогу — в любом классе, с учениками любого уровня, при изучении любого предмета — и не требует дополнительных затрат. Когда учителя преподносят материал в рамках многопланового подхода, они сами чувствуют вдохновение и начинают более креативно воспринимать свой предмет и способы его преподавания. Это, в свою очередь, порождает радость и ощущение успеха, особенно когда педагоги видят вовлеченность учеников.
Обе мои дочери ходили в начальную школу в Пало-Альто. Домашних заданий было немного, и это мне нравилось, поскольку я знаю, что их польза невелика (если она вообще есть), а занятия дома часто наносят вред самочувствию детей. По математике обычно надо было решить головоломки или кен-кены (японские математические загадки), но иногда девочки приносили домой страницу рабочей тетради с практически одинаковыми примерами. Это задание часто доводило их до слез. Я никогда не понимала, почему учителя полагают, будто уставшие дети будут по вечерам сидеть над монотонным, скучным материалом. Если я устаю, то прекращаю работу, а моих детей заставляют ее делать!
Я всегда стараюсь поддерживать учителей моих дочерей, потому что знаю: преподавание — одна из самых сложных и ответственных профессий, а педагоги — почти всегда прекрасные и заботливые люди. Однако однажды вечером я все-таки решила вмешаться. Моя младшая дочь, которой было почти девять, пришла домой со списком из 40 примеров. Она села за стол и уставилась на него потухшим взглядом. Я испугалась, что подобное задание отвратит дочку от математики, поэтому попросила ее решить только первые пять из них. Затем на том же листе написала педагогу записку.
Я попросила свою дочь решить первые пять примеров и увидела, что она поняла материал. Я позволила ей не выполнять остальные задания, потому что не хочу, чтобы она решила, будто только из этого и состоит математика.
Когда я цитирую эту записку другим учителям, они обычно смеются, вероятно, чувствуя облегчение при мысли, что это не они оказались на месте учителя моей дочери. Хорошая новость — именно в данном случае мы добились позитивного результата. Я поговорила со школьным преподавателем о нейробиологии и разнообразии подходов. Теперь вместо длинных списков заданий она дает ученикам четыре примера и предлагает решить их разными способами — с помощью чисел, рассказав историю и визуально.
Избавление от длинных перечней однотипных задач стало для дочери настоящим освобождением. Она больше не рыдала над домашней работой, с радостью сочиняла истории и рисовала картинки. В процессе выполнения заданий у нее активизировались и взаимодействовали разные участки мозга, и дочь в итоге получила возможность глубже усвоить материал.
Разнообразие подходов в работе с материалом не только повышает коннективность мозга, но и добавляет новое измерение жизни. Большинство учеников воспринимают математику как набор чисел и правил, а английский язык — как набор книг и слов. Подходя к изучению математики, литературы или физики как к возможности для творчества, пытаясь взглянуть на одни и те же вопросы с разных сторон, мы стимулируем рост мозга и нейронных связей. Когда благодаря педагогам учебный материал становится многоплановым, а списки однотипных задач, тексты из учебников или уравнения сменяются визуализацией, моделями, историями, видео, музыкой и рисунками, то обычный школьный класс превращается в место, откуда изгнана рутина и где приветствуется творчество в самых разных проявлениях.
Мне нравится иллюстрировать многоплановый подход к материалу картинкой из семи точек. Я говорю ученикам, что покажу ее на очень короткое время и попрошу ответить, сколько точек нарисовано, причем считать надо не по одной, а попробовать мыслить блоками. Затем выясняю, как именно они их группировали. Вот эти семь точек (рис. 4.4).

Рис. 4.4. Упражнение на запоминание: сколько существует вариантов, чтобы сгруппировать семь точек?
Недавно я дала это упражнение ученицам средней школы — они обнаружили 24 способа группировки! Девочки хотели еще пофантазировать, но подходило время обеда и урок пришлось завершить. Вот их 24 способа представления семи точек (рис. 4.5).
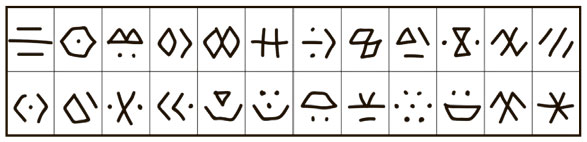
Рис. 4.5. Визуальное представление семи точек 24 разными способами
Я прошу учащихся выполнять это задание отчасти для того, чтобы проиллюстрировать креативность математики — даже на уровне семи точек! Но это упражнение одновременно развивает участок мозга, отвечающий за интуитивное чувство числа (ANS). Оно позволяет оценить размер группы однотипных предметов на глаз. Как выяснилось, по степени развитости ANS можно точно спрогнозировать успеваемость по математике.
Мы показываем ученикам сцену из фильма «Убить пересмешника», схему строения клетки или рассказываем о каком-нибудь событии, современном или историческом, и спрашиваем: «Что вы видите? Какие выводы вы можете сделать?» Это активизирует визуальное мышление и мультиплицирует количество идей, рождающихся у учеников, что всегда следует поощрять и приветствовать.
Когда педагоги учат многоплановому подходу и используют его
Калифорнийская долина — менее известный район Калифорнии по сравнению с городами на севере (Сан-Франциско) и юге (Лос-Анджелес). Когда я впервые поехала из Стэнфорда в Туларе, что примерно в 200 милях от университета и более чем в 100 милях от побережья, то знала, что в Калифорнийской долине пейзаж резко поменяется: вместо шоссе с домами и магазинами по обеим сторонам — кукурузные поля, тянущиеся на несколько миль.
Это аграрный регион с высокими потребностями и низкими результатами. Чиновники департамента образования округа Туларе ощущают, что региону не хватает условий для профессионального развития учителей. Недавно ко мне в Стэнфорд приезжала Шела Фельдстайн, методист округа по математике. У нее возникла идея собрать всех учителей пятых классов из нескольких районов и записать на мой онлайн-курс «Как преподавать математику». Проходить курс предлагалось группами, которые в оплачиваемое время вместе вырабатывали бы способы оптимизации школьного образования.
В течение года произошло много замечательных событий, что нашло отражение в научных публикациях, но больше всего меня порадовало, как изменился подход к преподаванию математики у самих учителей. До этого пятые классы считались классами с самой низкой успеваемостью — менее 8% учащихся достигали базового уровня овладения предметом (proficiency). В интервью по окончании учебного года педагоги признавались, что ранее испытывали страх во время уроков по математике и стремились завершить их как можно быстрее. Однако рассказ о типах мышления, росте мозга, многоплановом подходе к задачам понравился им настолько, что они до семи вечера обсуждали визуальный подход к решению задач. Один из преподавателей пятых классов по имени Джим добавил, как упражнение со складыванием бумаги помогло его ученикам лучше понять принцип возведения в степень. И это доставило ему огромную радость.
Они начали складывать треугольники из квадратного листа бумаги. И тут осознали, что такое степень числа: когда они складывают лист один раз, получаются два треугольника, а когда дважды, то уже четыре. Затем они обнаружили, что каждое складывание — по сути, возведение в квадрат. А потом сами стали выявлять закономерности. Мы оперировали числом 10 и показателем степени 10. Я наблюдал, как они связывают одно с другим, и это произвело на меня неизгладимое впечатление.
В сложных математических задачах учителя пятых классов увидели возможность применить креативный подход, и их мышление изменилось во многом благодаря знаниям нейробиологии, изложенным в предыдущих главах. До онлайн-курса у большинства педагогов мышление было фиксированным, они не ощущали смелости освоить и применить иные подходы. Теперь они смогли переосмыслить преподавание математики и других предметов. Одна учительница поразилась, насколько онлайн-курс изменил ее как личность.
Я думала, что для детей такой подход будет идеален. Но никогда не подозревала, что курс изменит меня. Это стало для меня самым большим откровением.
Иным сделалось мышление не только учителей. Когда они рассказали о мышлении роста своим ученикам, жизнь школьников также изменилась. В частности, поменялось их представление о собственном потенциале и перспективах. В изучении математики они теперь видели просто еще одну форму активности. Вот как рассказывает об этом школьный преподаватель.
Дети подбегали ко мне как заведенные: «О боже, он это вот так делает! А это ничего, что нам трудно? Нормально, что мы мыслим по-разному?»
Когда ученики задают подобные вопросы, становится очевидно, что они по-прежнему находятся во власти пагубных идей, сдерживающих их обучение. Допущение, что иное мышление или трудности не могут быть нормой, трагично само по себе, но еще более печально, что его разделяют миллионы учащихся, особенно в отношении математики. Когда у детей меняются представления о ценности проблем, когда они учатся смотреть на математику по-иному, их уверенность в себе возрастает, и это сразу же видят учителя, как отмечает в интервью Мигель:
Я только хочу сказать, что это [онлайн-курс] имело огромное значение. Увидеть, как дети начинают позитивно относиться к учебе, — значит полностью изменить мир. Я никогда не видел, чтобы они были так в себе уверены.
Учащиеся, перестроившие свое мышление и подход к обучению, принявшие трудности как норму и стремящиеся проанализировать задачи с разных сторон, получают весомые выгоды. Хотя тесты по математике — весьма однобокий инструмент оценки, тем не менее в конце учебного года те, кто учился у преподавателей, прошедших онлайн-курс, показали значительно более высокие результаты, чем ученики других классов. Самый большой прогресс наблюдался у девочек, language learners и детей из социально неблагополучных семей — именно среди тех, кто чаще не успевает по математике и другим предметам.
Одним из педагогов, прошедших онлайн-курс и затем использовавших новые знания, стала Джин Мэддокс. Весь год она не уставала рассказывать ученикам о возможностях постоянно расти и освоить все что угодно, призывала отбросить мысль об ограниченности собственного потенциала. Для Джин принципиально важную роль сыграли визуальные инструменты, они изменили ее собственный подход к математике и к преподаванию.
Когда все только начиналось, я действовала по одному алгоритму, потому что он был моей «страховочной сеткой». А теперь думаю так: «Отлично, как мне это нарисовать? Как представить визуально?» Я понимаю, почему алгоритм работает, теперь у меня в голове совершенно ясная картина. Особенно ярко это проявилось на теме дробей. Дети тут же сказали: «А, вот как это получается!» Они поняли, что любое математическое действие можно визуализировать, и тогда кто-то воскликнул: «О боже!» Да, те, кто раньше сводил математику к зубрежке фактов и правил, теперь испытывали восторг понимания: «О!»
Изменения, произошедшие с учителями, иллюстрируют двойную природу безграничного подхода — он меняет мышление и наши представления о себе, и отныне вы на любой материал и любую жизненную ситуацию будете смотреть многопланово.
Я предложила учителям пятых классов отказаться от вопросов, предполагающих ответ на автомате, и давать задачи, стимулирующие поиск неочевидных решений. Вот что сделала одна из педагогов.
Однажды я написала на доске: «Ответ — 17. Сколькими способами мы можем его получить?» Я думала, они начнут говорить 1 + 16, но дети предложили множество разных вариантов, при этом они от души веселились, что меня очень впечатлило.
Педагог рассказала в своем Twitter, что использовала ту же самую идею на уроке геометрии в старших классах. Написала ответ на доске и попросила учеников обосновать его, используя недавно пройденное. По ее словам, она была потрясена тем, какие разные креативные подходы использовали ученики, каким богатым материалом для последующего обсуждения это оказалось и какие возможности открылись для формирования нейронных связей в мозге.
Другая учительница пятых классов говорит, что теперь она просто показывает визуальное выражение математической идеи и спрашивает: «Что вы видите? А чего не видите? Что вы можете увидеть? Что могло бы стать продолжением?»
Все эти идеи совершенно не сложные, они строятся вокруг принципа разнообразия методов обучения. Они поощряют учащихся применять самые разные подходы, максимально далекие от традиционных. Учителя, меняющие свои методы, начинают легко оперировать материалом и ощущать свободу, которую дает такой подход к преподаванию: вместо того чтобы следовать за учебником, они экспериментируют и приглашают учеников экспериментировать вместе. Мы уже знаем, что многоплановый подход в обучении повышает коннективность мозга, способствует превращению подростков в успешных взрослых, которые, возможно, станут новаторами в своих областях.
Опыт подобных изменений имеется не только у учителей пятых классов из Калифорнийской долины. Холли Комптон до сих пор вспоминает, какой страх ее охватил, когда в первом классе ей нужно было прорешать целую страницу примеров с многозначными числами. Она, как и ее мать, сделала вывод, что у нее «не математический» мозг. За этим последовали годы фрустрации и походов к психологу. Отношения с математикой не задались из-за рабочей тетради, и в результате она решила, что математика не для нее.
К сожалению, математика быстрее любых других школьных предметов подрывает у учащихся веру в себя. Отчасти это происходит вследствие неправильных методов преподавания, что уже в первом классе вызывает такие сильные переживания, как у Холли. Но еще и из-за стереотипа, распространенного в нашем обществе: люди, успевающие по математике, действительно умны, а те, кому она дается с трудом, умом не блещут. На многих детей это действует деструктивно; среди таких оказалась и Холли. К сожалению, случай с Холли вряд ли является исключением. Вот как негативный опыт в математике повлиял на нее.
Он оказался поистине грандиозным. Всю свою жизнь я жила с клеймом неуверенности в себе.
К счастью, Холли усвоила новые представления о себе и своих способностях к обучению, что помогло ей освободиться от деструктивных установок. Решающим шагом стало понимание, что математические задачи можно решать разными способами. В этом и заключается значимость многопланового подхода к усвоению новых знаний. Холли признаётся в интервью:
Теперь математика стала для меня самым креативным предметом, потому что все можно «разобрать» на части, а потом сложить обратно и ты можешь целый час обсуждать, как сложить 13 и 12!
Холли заново выучила математику, и подтолкнули ее к этому ученики и их новое мышление. Когда дети начали решать задачи по-другому, она осознала, что математика совсем не тот предмет, каким она его воспринимала ранее. Она стала экспериментировать с примерами, и вскоре успеваемость всего класса выросла. После нескольких лет успешного преподавания Холли пригласили на должность куратора математического образования в округе — значимое достижение для человека, который раньше боялся математики. Теперь Холли отмечает, что ее метод преподавания призван развивать мышление роста, она дает сложные задачи, требующие многопланового подхода, и постоянно повторяет ученикам, что они преодолеют все трудности.
Помимо изменений в методиках преподавания, избавление от пагубных установок перестроило и формат коммуникации с людьми, еще раз подтвердив выгоду неодномерного подхода к жизненным ситуациям. Раньше Холли приходила на совещания в страхе, что она не знает того, что ей необходимо знать, и с уверенностью, что она должна быть экспертом в своей области. Сбросив оковы фиксированного мышления, она стала увереннее чувствовать себя на встречах и теперь чаще готова идти на риск:
Я не боюсь произносить подобные вещи. Я могу сказать другому педагогу: «Слушай, я застряла. Давай подумаем об этом вместе!»
Открытость новым вызовам и принятие неопределенности, вероятно, общая реакция на обретение свободы. Люди осознают, что бороться с трудностями — хорошо, это признак не слабости мозга, а его роста. В результате усиливается уверенность в себе, желание поделиться даже теми идеями, в правильности которых человек не до конца уверен. Одна из самых печальных системообразующих характеристик фиксированного мышления — страх оказаться неправым. Мозг человека буквально блокируется этим страхом. А подход, основанный на многоплановости, росте и борьбе с трудностями, освобождает. Холли призналась: «У меня появилось столько идей, потому что я позволила им родиться».
Важное преимущество многопланового подхода к работе и жизни в целом — уверенность, что если перед вами возникли препятствия, вы всегда найдете обходные пути. Многие взрослые, с которыми я беседовала, признавались, что они больше не останавливаются, сталкиваясь с вызовами и преградами, а ищут другую стратегию. Многоплановый подход к знанию показывает, что к результату можно прийти разными путями и одного единственно верного не существует, в любом случае есть несколько способов двигаться вперед.
Очень важно, что теперь идеи рождаются у Холли свободнее. Это одно из проявлений глубинных преобразований, происходящих с нами при освоении ключевых навыков обучения. В какой бы сфере вы ни работали, в образовании или в любой другой, понимание ограничений фиксированного мышления и возможностей для обучения и роста сделает вашу жизнь многограннее. Вырастет и уверенность в себе, и адаптивность, и удовлетворенность работой и отношениями с людьми.
Холли призналась, что ее взаимодействие с окружающими улучшилось, она перестала сомневаться в себе и впадать в депрессию. Удивительно, но это произошло после того, как она смогла по-новому взглянуть на математику и свои отношения с ней.
Для Холли ключевым фактором стало представление о математике как о дисциплине, к которой можно подойти с разных сторон, и осознание ценности разнообразных подходов. Открывая свой разум и начиная видеть безграничный потенциал — свой и других людей, вы вскоре обнаружите, что эффект будет сильнее, если осваивать материал с разных сторон. Многомерность — идеальное дополнение к мышлению роста. Вместе они дают гораздо более выраженный эффект.
Одним из факторов успеха нашего летнего лагеря, обеспечившего за смену в 18 дней прогресс, который соответствовал 2,7 года в школе, стал многоплановый подход. Когда год спустя мы опрашивали учащихся, кто-то из них рассказывал, что даже когда им задают прорешать целую страницу примеров, они забирают ее домой и решают вместе с родителями визуальными методами. Одна девочка с сожалением поведала, что уроки математики стали ей скучны, ведь учитель всегда требует решать задачи стандартно. Мне было печально слышать это, но я понимаю, что девочка уже знает о существовании разных типов мышления, а не одного-единственного — учительского, и, хотя ей не позволяют пользоваться собственными методами, не забывает об их значимости. Девочка была разочарована, но перспектива свободного мышления по-прежнему оставалась для нее реальной.
Часто ученики не знают, как подступиться к упражнениям, которые им задают. Это порождает негативные мысли как о себе, так и о своем обучении. Но когда те же задачи формулируются в доступной для всех форме, при этом выводят на новый уровень трудностей, каждый находит свои методы решения и достигает цели.
В лагере мы всегда использовали задания такого типа и поощряли разные способы рассуждения, разное видение задач, разные стратегии и методы. Мы приветствовали бурные дискуссии, в ходе которых ученики делились своим видением и решением, а мы обсуждали и сравнивали разные подходы. Благодаря этому занятия проходили эффективно, а у детей появлялась мотивация к изучению предмета. Мы обеспечивали им возможность подступиться к задаче, показывали, какими способами можно получить ответ. В этом и заключается союз мышления роста и многоплановости, которого так часто не хватает в классах, дома и в офисах.
Учащимся очень трудно освободить сознание и развивать безграничный разум, когда в школе им не дают ничего, кроме стандартных тестов и контрольных, а также постоянно напоминают о фиксированности мышления. Учителя, с которыми я беседовала, отличаются от большинства своих коллег, потому что понимают ценность снятия ограничений. Для достижения этой благородной цели они сочетают работу, стимулирующую рост мозга и мышление роста, с подходом к преподаванию и оценке, который способствует прогрессу и любознательности.
Я использую многоплановый подход в преподавании математики студентам. Мы проводим десять недель, рассматривая математические концепции визуально, иногда объектно, а также алгоритмически и с помощью чисел. Все это укрепляет нейронные связи в мозге. Вот анонимная оценка курса от одного из студентов.
Математика всегда существовала на бумаге, по крайней мере для меня. С началом этого курса задачи перешли в какое-то трехмерное пространство. Стены комнаты, обратная сторона бейджа, который вы попросили сделать, блокнот для гуманитарных предметов — эти квадраты и диаграммы заполнили ту часть мозга, которую я отводил для счета. Раньше всё было одномерным, имело одно решение. Теперь пространство, оставляемое для математики, расширилось экспоненциально.
Другие студенты также отмечали, что благодаря визуальному, креативному подходу к математике, знаниям из сферы нейробиологии, информации о типах мышления их мозг стал более пластичным и это преобразило их жизнь и позволило добиться успехов. Они смогли взять самые разные курсы в Стэнфорде.
Жизнь Марка Петри радикально изменилась после того, как он осознал преимущества борьбы с трудностями и разнообразных подходов к изучению материала. Марку уже за 60. В детстве он попал в аварию, в результате которой частично стал инвалидом. Его мать отказалась признать, что сын никогда не восстановится и его придется отдать в коррекционную школу, и сама занялась его лечением. Координацию она развивала, бросая сыну мешочки с фасолью, а он должен был ловить их. Когда Марк подрос, он стал учиться кататься на коньках. Постоянно падал и поднимался, падал и вставал вновь. Детские годы сформировали у него мышление роста: «Без этого, — говорит он, — я бы вообще ничего не добился». Когда Марк прочитал о преодолении трудностей в моей предыдущей книге, он тут же связал это с собственной жизнью и с тем, как такая борьба сформировала его личность.
Мышление роста сформировалось у Марка еще в детские годы, но именно благодаря вебинару на канале Youcubed он усвоил язык, на котором смог разговаривать с учениками восьмого класса. До посещения вебинара Марк преподавал по не самым вдохновляющим учебникам. После летнего вебинара он вернулся в школу в Санта-Ане и поменял методику.
Каждый понедельник он начинал урок с видео, героем которого был человек с мышлением роста. В день нашего интервью Марк показывал ролик о 15-летнем подростке, разработавшем тест на рак поджелудочной железы. Он находит эти видео в интернете, и все они демонстрируют тип мышления в действии. Каждую среду Марк представляет свой любимый «нет»-пример — математическую задачу с ошибками, которые учащиеся должны обнаружить сами. По пятницам ученики работают над математическими и художественными проектами. Помимо этого еженедельного плана занятий, Марк применяет многоплановый подход постоянно, призывая учеников рисовать комиксы для иллюстрации математических концепций либо визуально представлять математические модели, а потом спрашивает, что именно те видят. И на уроках математики, и на уроках по творчеству он показывает ученикам картины и рисунки, после чего также спрашивает, что они видят. Марк предлагает школьникам создавать коллажи из узоров и орнаментов, изучать работы великих мастеров, анализируя, к примеру, проявления симметрии в их произведениях.
Ранее лишь 6% учеников Марка осваивали математику на базовом уровне. После внедрения многопланового подхода этот показатель возрос до 70%. Марк много рассказывал об использовании разнообразных и прекрасных методов преподавания математики — через искусство, кино и другие креативные способы. Я спросила у него, пользовался ли он при этом учебником. Марк объяснил, что ему удавалось добиваться гораздо большего, если школьники изучали материал учебника не более 25–30 минут, а оставшееся от 55-минутного урока время посвящали другим проектам. Это решение кажется мне разумным.
Марк принял подход, основанный на мышлении роста, не только в преподавании математики, но и в жизни. Несколькими годами ранее, когда его сын был еще маленьким, у его жены обнаружили рак и ей пришлось перенести пять операций. Несмотря на хирургические вмешательства и полтора года химиотерапии, она продолжала вести адвокатскую практику. В то время Марку приходилось напрягать все силы, чтобы заботиться о жене, сыне и преподавать. По признанию самого Марка, он был «максимально позитивным, насколько это возможно». Сейчас его сын учится в колледже, а у жены наступила ремиссия, и по субботам они вместе пекут печенье для живущих в приютах. А жена к тому же вяжет головные уборы для женщин, проходящих химиотерапию. Марк пришел к тому типу мышления, который я наблюдаю у всех интервьюируемых, выбравших безграничный подход. Этот подход заключается в том, чтобы превращать негатив в позитив. Он упоминал о принципе, который в иудаизме называется «тиккун олам» — «исправление мира» — и также связан с мышлением роста. Марк рассуждает так: «Для меня это как задаваться вопросом: “Зачем я на этой планете? Зачем я здесь? Зачем я в этом классе? Должна быть какая-то причина”».
Позитивный подход к жизни, демонстрируемый даже в самых тяжелых ситуациях, очень вдохновляет. Изменения, внедренные Марком на занятиях, не только заметно повысили успеваемость учащихся, но и повлияли на его коллег-педагогов. Когда учителя шестых-седьмых классов увидели, каких успехов добился Марк в восьмом классе, они начали следовать некоторым его идеям и также заметили, как возросла успеваемость их учеников.
Использовать многоплановый подход может преподаватель любого предмета. В конце книги вы найдете ресурсы для визуального представления математики. Если учителя строят урок по-старому, дети могут освоить этот новаторский подход самостоятельно.
Я уже говорила о летней смене с 84 школьниками, приехавшими в кампус Стэнфорда. Когда на следующий год мы опросили тех же учеников, один мальчик сообщил, что он лучше понял концепцию объема, потому что теперь думает о кубиках объемом в 1 см3 как о кусочках сахара, с которыми мы работали в лагере. К сожалению, многие из этих учеников не получают возможности продолжить визуальную работу с математическими объектами в своей школе, но после этих 18 дней их взгляд на обучение изменился и они могут применить полученные знания не только для учебы, но и в жизни.
Педагог Лея Хэйворт рассказала в интервью об огромных изменениях, которые произошли с учащимися, когда вместо учебников с правилами и упражнениями она вручила им толстые чистые блокноты и предложила «поиграть» с концепциями, рисовать их и размышлять над ними. Предоставление учащимся пространства для творчества, где они могут думать, исследовать, пробовать, — идеальное дополнение к многоплановому подходу в изучении материала.
Несколько лет назад я провела недельный эксперимент в местной школе — серию визуальных и творческих уроков математики, доступ к которым мы предоставили на нашем канале Youcubed. Когда после урока я шла по коридору, меня догнала мама одной ученицы и спросила, что мы делали последние несколько дней на уроках математики. Ее дочь, всегда ненавидевшая этот предмет и неспособная его усвоить, поменяла мнение! Теперь она видела свое будущее в математике. Слышать это было очень приятно, ведь мне известно: когда дети меняют отношение к собственным возможностям и принимают новые подходы, их жизненный путь также меняется.
Три ключевых навыка обучения, связанных с мышлением роста и вызовами, критически важны для высвобождения личностного потенциала. Вне надлежащего контекста для креативного развития мозга эти тезисы могут быть восприняты как досадные и контрпродуктивные. Когда человек с мышлением роста сталкивается с ограничениями мира фиксированного мышления, он теряет часть своего потенциала к переменам. Решение, как мы теперь знаем, лежит в плоскости многопланового обучения — это ключевой навык № 4. Взгляд на тему, задачу или мир в целом с разных точек зрения побуждает нас учиться и расти. Мышление роста вкупе с возможностями многопланового обучения позволит учащимся любого возраста избавиться от страха, преодолеть препятствия и обрести уверенность в своих силах. Даже если мы работаем внутри жесткой фиксированной системы, не признающей многообразие подлинной ценностью, — будь то школа, ориентированная на результаты тестов, или работа, где от вас нужны только узкие специальные навыки, — использование многопланового подхода к решению возникающих проблем поддержит вас и укрепит все направления вашего обучения и все аспекты вашей жизни.

