«Типичный» и «средний»
На протяжении большей части XX века Германия сохраняла добрые, взаимовыгодные отношения со своими соседями.
Все, с теорией мы закончили. Ну и что тут важного, какая разница – степенным законом или нормальным описывается распределение случайной величины, спросят некоторые. И как вообще это можно применить в жизни?
Во-первых, если распределение элементов описывается степенным законом, значит между этими элементами есть взаимосвязь. Это важно. Каждый выстрел из нашей пушки не зависит от предыдущего и не влияет на последующий. Но поведение каждого участника в группе зависит от других участников. Решения о покупке или продаже акций на бирже определяются другими участниками торгов. Решение свести счеты с жизнью зависит от других самоубийц и влияет на последующих. Землетрясение, произошедшее сегодня за 5 тысяч километров, может вызвать землетрясение у вас дома через пару дней. Бабочка, взмахнувшая крыльями в Айове, может вызывать ураган в Индонезии.
Знание взаимозависимости между элементами в сложных системах помогает нам вывести два наиважнейших пункта:
1. Так как ни одна компьютерная программа никогда не сможет учесть поведение абсолютно всех элементов в сложных самоорганизующихся системах, то их поведение после преодоления точки бифуркации предсказать невозможно.
2. Вы, как один из элементов сложной самоорганизующейся системы, можете оказывать влияние на другие элементы. Даже если они расположены в тысячах километрах от вас. И даже через десятки и сотни лет ваше влияние все еще будет ощущаться.
Оба эти пункта мы рассмотрим в следующих главах.
И второй вывод, который можно сделать на основании факта взаимозависимости: в системах, которые описываются степенным законом, нельзя использовать категорию «типичный», там ее просто не существует. И это важнейшее свойство, а не малозначительная деталь. Отсутствие такой категории, как «типичность», затрудняет процессы прогнозирования, сравнения и оценки. А иногда делает и вовсе невозможными.
Давайте для контраста рассмотрим понятие «типичный» в системах, в которых нет взаимозависимости между элементами (правильнее их будет называть все же не системы, а совокупности, нагромождения и пр.). Например, типичный, то есть наиболее распространенный рост мужчины, примерно 1 метр 80 сантиметров. Теперь я могу сказать, что мой рост (примерно 1,78 м) не сильно отличается от среднего, это значит, что я почти типичный представитель мужского пола (с точки зрения роста). При этом мы твердо знаем, что 99,7 % всех мужчин будут попадать в диапазон 1,8 метра плюс-минус 3 сигмы. Рост одного из миллиона мужчин будет отличаться от среднего на 5 сигм. А вот мужчин ростом 1,8 метра плюс 10 сигм не существует. Последнее утверждение является истинным с вероятностью 100 %.
Знание среднего, то есть типичного, роста позволяет оценивать и проводить сравнение и, что немаловажно, прогнозировать. То есть вы, являясь представителем сильного пола, можете сравнить свой рост с типичным показателем, оценить, насколько вы выше или ниже среднего, сделать соответствующие выводы, весьма достоверные прогнозы и даже сформулировать рекомендации. Если ваш рост превышает средний показатель на 20 сантиметров, добро пожаловать в баскетбольную команду и будьте добры покинуть список претендентов в танковые войска. Если оценки вашего ребенка на 30 % ниже среднего (типичного) балла по школе, то вы уже знаете, чем стоит занять его ближайшим летом и во что эффективнее всего инвестировать свободные денежные средства.
Другими словами, категория «типичный» оказывает весьма эффективную помощь при прогнозировании и принятии решений. Она снижает степень неопределенности. А вот ее отсутствие усложняет эти процессы, а иногда и вовсе делает их невозможными.
Посудите сами, разве представленный выше график распределения городов в зависимости от количества проживающих в них жителей позволит вам ответить на вопрос, какой город является «типичным»? Тот, в котором проживает 10 миллионов населения? С одной стороны – да, ведь это крупные города. Но с другой стороны – нет, ведь таких городов очень мало, просто ничтожно мало на фоне общего количества маленьких городков. Или, может быть, «типичен» небольшой городок, в котором проживает до 100 тысяч населения? Ведь таких городков очень много! Много, это верно, но только количество жителей больно уж невелико, не тянет такой городок на «типичный». Обратите еще раз внимание на график нормального распределения независимых величин. На нем четко прослеживается тенденция тяготения всех значений к некоторому среднему, типичному. При степенном распределении (то есть при наличии взаимозависимости) такого тяготения к среднему нет и быть не может, потому что самого среднего не существует. Нет типичных объектов в подобных системах!
Здесь мы уходим в область прогнозирования. Если случайная величина (такая, как рост мужчины) описывается нормальным законом распределения, то мы можем с высокой долей вероятности определить, какой рост вон у того мужчины, что стоит перед нами в очереди в кассу. И мы точно знаем, что его рост не 3 метра и не 17 сантиметров, даже если мы его никогда прежде не видели и ничего про него не слышали.
А вот степенной закон не накладывает никаких ограничений на прогнозные значения. И это очень важное, я бы сказал, ключевое его отличие от нормального закона распределения.
Имея дело со сложной системой, описываемой степенным законом, мы не можем быть уверены, что никогда не встретим случайную величину, значительно выбивающуюся из тех, что наблюдали ранее. Другими словами, наш жизненный опыт не позволяет делать прогнозы в сложных системах. Это ключевая мысль этой главы. Сформулируем ее еще раз.
В сложных системах, описываемых степенным законом, мы не можем делать прогнозы на основании жизненного опыта!
Если самый крупный город, участвующий в нашей выборке, насчитывает 20 миллионов жителей, это не значит, что не бывает (и не может быть в будущем) городов с 30, 50 и даже 100 миллионами жителей. Если самый крупный за всю историю наблюдений обвал рынка ценных бумаг вызвал снижение фондового индекса в 10 раз, это не означает, что следующий обвал не приведет к снижению значения индекса в 15 или в 100 раз! Если за последние 20 лет в вашем городе с населением 10 000 человек не было зафиксировано ни одного случая самоубийства, это не означает, что в следующем году вы не прочитаете в газетах о 100 случаях (1 % населения), когда люди покончили с собой. Все, что нам нужно сделать, после того как мы стали свидетелями таких событий, это продлить нашу линию на графике до новых значений (с 20 миллионов жителей до 100, с десятикратного обвала фондового индекса до стократного и т. д.). Просто продлить, не удивляясь, не отсекая новые данные как чрезвычайно редкие и незначимые. Продлить и быть готовыми продлить еще раз через год, через тысячу лет или… завтра утром.
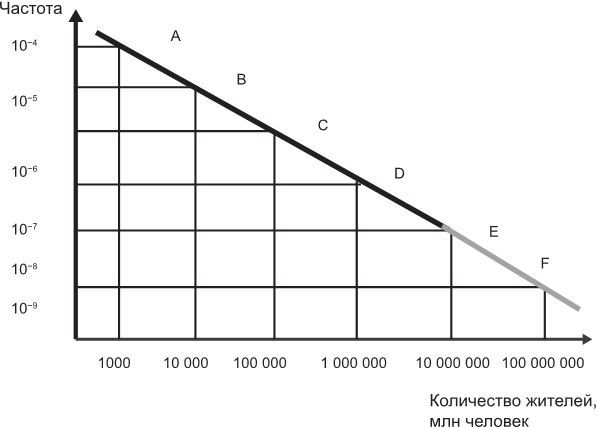
График (с продленной линией) распределения количества городов в зависимости от числа проживающих в них жителей
Да, такие события происходят крайне редко, раз в сто, тысячу, миллиард лет. Но их последствия носят катастрофический характер. Или как минимум существенно меняют нашу картину мира. И поэтому мы должны быть к ним готовы. Теперь чувствуете разницу между степенным и нормальным законом распределения?

