Отец Альберта Эйнштейна строил электростанции в Италии. Когда Альберт был ребенком, уравнениям Максвелла было всего несколько десятков лет от роду, но Италия уже входила в эпоху промышленной революции, и турбины с трансформаторами, которые строил отец Эйнштейна, основывались на этих уравнениях. Мощь новой физики была очевидна для всех.

Альберт был бунтарем. Родители оставили его в Германии для завершения школьного образования, однако он считал немецкую школьную систему слишком жесткой и военизированной; он не смог смириться со школьными порядками и бросил учебу. Вернувшись к родителям в Италию, в Павию, он проводил время в безделье. Затем он отправился учиться в Швейцарию, но не смог сразу поступить в Цюрихский политехникум, куда стремился. После университета он не смог получить исследовательскую позицию и, чтобы заработать на жизнь себе и своей гражданской жене, нанялся на работу в патентный офис в Берне.

Это было не самое завидное место для дипломированного физика, однако оно обеспечило Альберту время для размышлений и независимой работы. И он размышлял и работал. В конце концов, именно этим он занимался с самой ранней юности: вместо того чтобы учиться в школе, он читал «Начала» Евклида и «Критику чистого разума» Канта. Ведь невозможно попасть в новые места, следуя проложенным трассам.

В возрасте 25 лет Эйнштейн отправляет в Annalen der Physik три статьи. Каждая из них была как минимум достойна Нобелевской премии и даже большего. И каждая стала опорой для нашего понимания мира. Я уже рассказывал о первой из этих статей, в которой молодой Альберт вычислил размеры атомов и доказал спустя 23 столетия, что идеи Демокрита были верны – материя зерниста.

Вторая статья принесла Эйнштейну наибольшую славу – именно в ней он представил свою теорию относительности. Именно теории относительности и посвящена эта глава.

На самом деле существует две теории относительности. Конверт, отправленный в редакцию двадцатипятилетним Эйнштейном, содержал изложение первой из них – теории, которую сегодня мы называем специальной теорией относительности. Она дает важное уточнение структуры пространства и времени, которое я проиллюстрирую здесь, прежде чем переходить к другой, более важной, теории Эйнштейна – общей теории относительности.

Специальная теория относительности – это тонкая и концептуально сложная теория. Ее труднее усвоить, чем общую теорию относительности. Читателю не следует пугаться, если следующие несколько страниц покажутся ему не очень простыми для понимания. Эта теория впервые показывает, что в ньютоновской картине мира не просто чего-то не хватает, но она должна быть радикально изменена, причем таким образом, что станет полностью противоречить здравому смыслу. Это первый реальный шаг к пересмотру наших самых глубоких интуитивных представлений о мире.

Теории Ньютона и Максвелла противоречат друг другу в одном тонком моменте. Из уравнений Максвелла выводится величина скорости – скорости света. Однако ньютоновская механика несовместима с существованием фундаментальной скорости, поскольку в уравнения Ньютона входит ускорение, а не скорость. В ньютоновской физике скорость может быть только скоростью чего-то относительно чего-то другого. Галилей подчеркивал тот факт, что Земля движется относительно Солнца, даже если мы не воспринимаем это движение, поскольку то, что мы обычно называем скоростью, – это скорость относительно Земли. Именно это мы имеем в виду, говоря, что скорость – это относительная величина, то есть скорость объекта самого по себе не имеет смысла, единственная скорость, которая существует, – это скорость одного объекта относительно другого. Это то, что изучали студенты-физики в XIX веке, и то, что они изучают сегодня. Но если это так, то относительно чего определена скорость света, выводимая из уравнений Максвелла?

Одна из возможностей разрешения этого спорного вопроса состоит в том, что существует некая универсальная среда, по отношению к которой свет и движется со своей скоростью. Однако положения теории Максвелла выглядят независимыми от этой среды. Все экспериментальные попытки измерить скорость Земли по отношению к этой гипотетической среде, предпринимавшиеся в конце XIX века, закончились неудачей.

Эйнштейн утверждал, что на верный путь его навели не эксперименты, а только видимые противоречия между уравнениями Максвелла и механикой Ньютона. Он задался вопросом: можно ли каким-то образом совместить ключевые открытия Ньютона и Галилея с теорией Максвелла?

Занимаясь этим, Эйнштейн пришел к удивительному открытию. Чтобы понять его, подумайте обо всех прошлых, настоящих и будущих событиях (по отношению к тому моменту, когда вы читаете этот текст) и представьте их изображенными как на рис. 3.1.

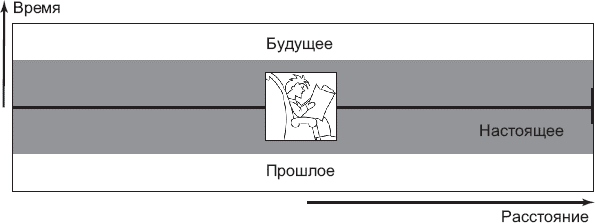
Рис. 3.1. Пространство и время до Эйнштейна

Итак, открытие Эйнштейна заключается в том, что эта схема некорректна. В действительности все устроено примерно так, как показано на рис. 3.2.

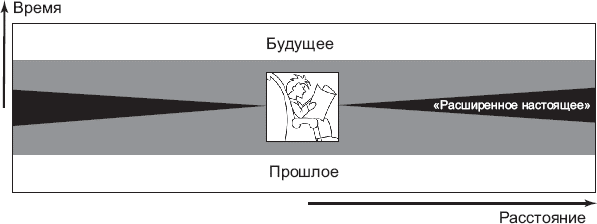
Рис. 3.2. Структура пространства-времени. Для каждого наблюдателя «расширенное настоящее» – это промежуточная зона между прошлым и будущим

Между прошлым и будущим для некоторого события (например, между прошлым и будущим для вас, там, где вы в данный конкретный момент находитесь) существует «промежуточная зона», или «расширенное настоящее», зона, которая не является ни прошлым, ни будущим. Это открытие сделано в рамках в специальной теории относительности.

Длительность этой промежуточной зоны, которая не находится ни в вашем прошлом, ни в вашем будущем, очень мала и зависит от того, где относительно вас происходит событие (см. рис. 3.2): чем больше расстояние от вас до события, тем больше длительность расширенного настоящего. На расстоянии нескольких метров от вашего носа, дорогой читатель, продолжительность того, что является для вас промежуточной зоной (ни прошлым, ни будущим), не превышает нескольких наносекунд – это почти ничто (в одной секунде столько же наносекунд, сколько секунд в 30 годах). Это намного меньше, чем вы способны заметить. На другой стороне океана длительность этой промежуточной зоны составляет тысячную долю секунды, что всё еще ниже порога нашего восприятия времени: минимальный отрезок времени, который мы способны ощутить, – порядка сотой доли секунды. Однако на Луне продолжительность расширенного настоящего составляет уже секунды, а на Марсе – около четверти часа. Таким образом, можно сказать, что на Марсе есть события, которые в данный конкретный момент уже случились, события, которым еще предстоит случиться, но есть также четверть часа, в течение которых происходят события, которые не принадлежат ни нашему прошлому, ни нашему будущему.

Они находятся где-то еще. Никогда прежде мы не догадывались о существовании этого «где-то еще», поскольку вблизи нас это «где-то еще» слишком скоротечно; мы недостаточно проворны, чтобы его заметить. Но оно существует, и оно реально.

Именно поэтому нельзя поддерживать непринужденную беседу между Землей и Марсом. Допустим, я нахожусь на Марсе, а вы здесь. Я задаю вам вопрос, а вы отвечаете сразу, как только услышите, что я сказал; ваш ответ приходит ко мне спустя четверть часа после того, как я задал вопрос. Эта четверть часа – время, которое не является ни прошлым, ни будущим по отношению к тому моменту, когда вы мне ответили. Принципиальный факт, касающийся устройства мира, понятый Эйнштейном, состоит в том, что эта четверть часа неустранима: нет способа ее сократить. Она вплетена в ткань событий пространства и времени: мы не можем укоротить ее точно так же, как не можем послать письмо в прошлое.

Это странно, но наш мир устроен именно так. Это так же странно, как тот факт, что в Сиднее люди живут «вверх ногами»: странно, но правда. Мы привыкли к этому факту, который теперь кажется нормальным и разумным. Это структура пространства и времени, и она именно такова.

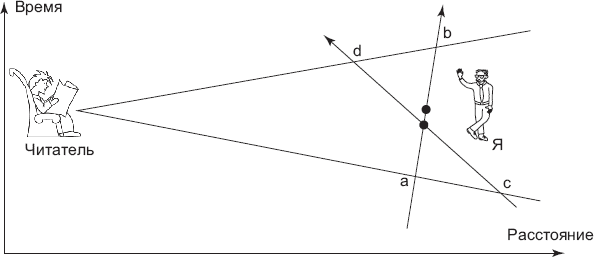
Рис. 3.3. Относительность одновременности

Из сказанного следует, что бессмысленно говорить о событии на Марсе, что оно происходит «прямо сейчас», просто потому, что никакого «прямо сейчас» не существует (рис. 3.3.).

Если выражаться более строго, то Эйнштейн понял, что не существует «абсолютной одновременности»: во Вселенной нет такого множества событий, которые происходят «сейчас». Совокупность всех событий во Вселенной нельзя описать как последовательность моментальных «сейчас» – настоящих, следующих одно за другим; она имеет более сложную структуру, показанную на рис. 3.2. Мы видим там то, что в физике называют пространством-временем – это набор всех прошлых и будущих событий, но также и тех, которые «ни в прошлом, ни в будущем»; последние не образуют единого мгновения: у них самих есть длительность.

Для галактики Андромеды длительность этого расширенного настоящего по отношению к нам составляет два миллиона лет. Все, что происходит в течение этих двух миллионов лет, не является ни прошлым, ни будущим по отношению к нам. Если бы дружественная высокоразвитая цивилизация в Андромеде решила отправить к нам с визитом эскадру звездолетов, то не было бы смысла спрашивать, эскадра «сейчас» уже вылетела или еще нет. Единственный осмысленный вопрос: когда мы получим первый сигнал от этой эскадры? Начиная с этого момента, но не ранее, отправление эскадры оказывается в нашем прошлом.

Открытие такой структуры пространства-времени, сделанное молодым Эйнштейном в 1905 году, имело серьезные последствия. Тот факт, что пространство и время тесно связаны между собой, как показано на рис. 3.2, потребовал тонкой реструктуризации ньютоновской механики, которую Эйнштейн быстро осуществил в 1905 и 1906 годах. Первый результат этой реструктуризации состоит в том, что пространство и время сплавляются в единую концепцию пространства-времени, а электрическое и магнитное поля аналогичным образом сплавляются в единую сущность, которую сегодня мы называем электромагнитным полем. Сложные уравнения, записанные Максвеллом для двух полей, значительно упрощаются, когда переформулируются на этом новом языке.

Есть еще один вывод этой теории, который влечет за собой очень серьезные последствия. В новой механике концепции энергии и массы объединяются и сплавляются воедино, подобно тому как объединились время и пространство, электрическое и магнитное поля. До 1905 года незыблемыми считались два общих принципа – сохранения массы и сохранения энергии. Первый из них был всесторонне проверен химиками: масса никогда не меняется в химических реакциях. Второй – сохранение энергии – непосредственно вытекал из уравнений Ньютона и рассматривался как один из самых бесспорных законов. Однако Эйнштейн понимает, что энергия и масса – это две грани одной сущности, подобно тому как электрическое и магнитное поля – это две стороны одного и того же поля, а пространство и время – две грани одной сущности, пространства-времени. Это означает, что масса сама по себе не сохраняется и энергия – как ее воспринимали в то время – тоже не является независимо сохраняющейся величиной. Они могут превращаться друг в друга: существует только один закон сохранения, а не два. Сохраняется сумма массы и энергии, но не каждая из них по отдельности. Должны существовать процессы, которые преобразуют энергию в массу, а массу – в энергию.

Несложный расчет показал Эйнштейну, как много энергии получается при преобразовании одного грамма массы. Результат выражается знаменитой формулой E = mc². Поскольку скорость света c – это очень большая величина, а c² – еще большая, энергия, получаемая из одного грамма массы, колоссальна. Это энергия миллионов одномоментно взорвавшихся бомб: ее достаточно, чтобы месяцами освещать город и питать промышленность страны или, напротив, чтобы в одну секунду уничтожить сотни тысяч человеческих жизней в таком городе, как Хиросима.

Теоретические рассуждения молодого Эйнштейна перенесли человечество в новую эру – эру ядерной энергии, новых возможностей и новых опасностей. Сегодня благодаря интеллекту этого молодого бунтаря, не выносившего жестких правил, мы получили средства, способные обеспечить светом жилища 10 миллиардов людей, которые вскоре будут населять нашу планету, средства для космических путешествий к другим звездам, а также средства, позволяющие уничтожить друг друга и разрушить планету. Все зависит от нашего выбора: каких лидеров мы призовем принимать для нас решения.

Сегодня структура пространства-времени, предложенная Эйнштейном, хорошо понята и многократно проверена в лабораториях, она считается надежно установленной. Время и пространство – не такие, какими они представлялись со времен Ньютона. Пространство не существует независимо от времени. В расширенном пространстве (рис. 3.2) нет какого-то выделенного среза, который с бо́льшим основанием, чем другие, можно было бы назвать «пространство сейчас». Наше интуитивное представление о настоящем как о единстве всех событий, происходящих «сейчас» во Вселенной, – это результат нашей слепоты, нашей неспособности воспринимать малые временные интервалы. Это необоснованная экстраполяция нашего ограниченного опыта.

Представление о настоящем, подобно представлению о плоской Земле, является иллюзией. Мы представляли себе Землю плоской в силу ограниченности наших чувств, поскольку мы не могли видеть намного дальше своего носа. Если бы мы жили на астероиде диаметром несколько километров, как планета Маленького Принца, мы легко представили бы себе, что находимся на сфере. Если бы наш мозг и наши органы чувств давали нам более точное восприятие и мы легко воспринимали бы наносекундные отрезки времени, нам никогда бы не пришло в голову, что «настоящее» простирается повсюду. Мы бы свободно воспринимали существование промежуточной зоны между прошлым и будущим. Мы бы хорошо понимали, что слова «здесь и сейчас» имеют смысл, но слово «сейчас», обозначающее события, «происходящие в данный момент» по всей Вселенной, не имеет смысла. Оно подобно вопросу о том, находится наша Галактика «выше или ниже» галактики в Андромеде, не имеет смысла, поскольку понятия «выше» и «ниже» наделены смыслом только на поверхности Земли, а не в космосе. Во Вселенной нет «верха» и «низа». И аналогичным образом два события в ней далеко не всегда связаны отношениями «до» или «после». Получившуюся в результате структуру из сплетенных между собой пространства и времени, как это изображено на рис. 3.2 и 3.3, физики называют пространством-временем (рис. 3.4).

Когда журнал Annalen der Physik опубликовал статью Эйнштейна, внезапно прояснившую все эти вопросы, это произвело грандиозное впечатление на физическое сообщество. Явные противоречия между уравнениями Максвелла и ньютоновской физикой были хорошо известны, но никто не знал, как их разрешить. Эйнштейновское решение, поразительное и чрезвычайно элегантное, стало для всех неожиданностью. Рассказывают, как в тускло освещенных старых залах Краковского университета строгий профессор физики, оторвавшись от своих занятий, потрясал эйнштейновской статьей и кричал: «Родился новый Архимед!»

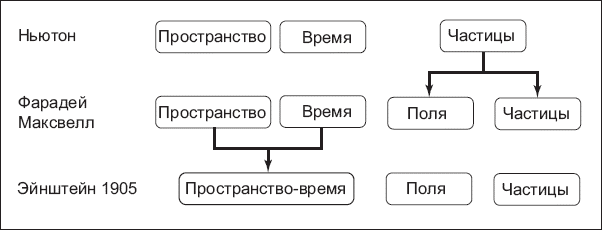
Рис. 3.4. Из чего состоит мир?

Но, несмотря на бурную реакцию, спровоцированную прорывом, который совершил Эйнштейн в 1905 году, мы еще не добрались до его подлинного шедевра. Триумфом Эйнштейна стала его вторая теория относительности – общая теория относительности, опубликованная десятью годами позднее, когда ему было тридцать пять.

Теория «общей относительности» – это самая красивая теория, порожденная физикой, и первый столп квантовой гравитации. Она является стержневой темой для всей этой книги. Именно здесь начинается подлинная магия физики XX века.

После публикации специальной теории относительности Эйнштейн становится знаменитым физиком и получает приглашения на работу от множества университетов. Но его продолжает кое-что беспокоить: специальная теория относительности не согласуется с тем, что известно о гравитации. Он понимает это в ходе написания обзора своей теории и задумывается, не следует ли пересмотреть общепризнанную теорию всемирного тяготения, созданную отцом физики Ньютоном, чтобы добиться совместимости с его теорией относительности?

Источник проблемы понять нетрудно. Ньютон хотел объяснить, почему предметы падают, а планеты вращаются по орбитам. Он придумал «силу», которая притягивает все тела друг к другу, – силу гравитации. Но каким образом этой силе удается воздействовать на удаленные предметы, когда между ними ничего нет, было непонятно. Сам Ньютон, как мы видели, подозревал, что в этой идее силы, действующей между далекими телами без соприкосновения, чего-то не хватает и что для притяжения Луны Землей между ними должно быть нечто, передающее эту силу. Два столетия спустя Фарадей нашел решение, правда, не для силы гравитации, а для электрических и магнитных сил – поле. Электрические и магнитные силы «переносятся» электрическими и магнитными полями.

На этой стадии любому рациональному человеку было очевидно, что сила гравитации тоже должна иметь свои фарадеевы линии. Также по аналогии было очевидно, что сила притяжения между Солнцем и Землей или между Землей и падающим предметом должна быть приписана полю – в данном случае гравитационному полю. Ответ на вопрос о том, что переносит силу, найденный Фарадеем и Максвеллом, очевидно, должен применяться не только к электричеству, но также и к гравитации. Должно существовать гравитационное поле, а уравнения, аналогичные максвелловским, должны описывать, как движутся фарадеевы гравитационные линии. В первые годы XX века все это было ясно любому достаточно последовательному человеку; иначе говоря, это было ясно только Альберту Эйнштейну.

Эйнштейн, которого с юности восхищало электромагнитное поле, толкавшее роторы на электростанциях его отца, начал задумываться о гравитационном поле и искать уравнения, которые могли бы его описать. Он полностью погрузился в эту проблему. На то, чтобы решить ее, ушло десять лет. Десять лет упорных исследований, попыток, ошибок, недоразумений, блестящих идей, неверных допущений, статей с некорректными уравнениями, новых ошибок, стресса. Наконец, в 1915 году он отправил в печать статью, содержащую исчерпывающее решение, которое он назвал общей теорией относительности, – свой шедевр. Лев Ландау, самый блестящий физик-теоретик Советского Союза, называл ее «самой красивой из всех существующих физических теорий».

Нетрудно понять, почему эта теория столь красива. Вместо простого изобретения математической формы для гравитационного поля и поиска искусственных уравнений для него Эйнштейн обращается к другому нерешенному вопросу, лежащему в самой глубине ньютоновской теории, и объединяет две проблемы.

Ньютон вернулся к демокритовской идее, согласно которой тела движутся в пространстве. Это пространство должно быть большим пустым вместилищем, «жесткой коробкой» для Вселенной, колоссальной сценой, на которой объекты движутся по прямым линиям, пока силы не вынудят их отклониться. Но из чего состоит само это пространство, которое содержит мир? Что есть пространство?

Идея пространства кажется нам естественной, но исключительно благодаря знакомству с ньютоновской физикой. Если задуматься, то пустое пространство не является частью нашего опыта. От Аристотеля до Декарта, то есть на протяжении двух тысячелетий, демокритовская идея пространства как особой сущности, отличной от вещей, вовсе не казалась разумной. И для Аристотеля, и для Декарта вещи имеют протяженность: протяженность – это свойство вещей, но протяженность не существует без чего-то протяженного. Я могу вылить воду из стакана, но тогда его заполнит воздух. Доводилось ли вам видеть по-настоящему пустой стакан?

Если между двумя вещами находится ничто, значит, заключает Аристотель, там нет ничего. Каким образом там может быть одновременно и нечто (пространство), и ничто? Что есть пустое пространство, внутри которого движутся частицы? Это нечто или ничто? Если это ничто, то оно не существует, и мы можем без него обойтись. Если это нечто, то может ли быть так, что его единственное свойство – ничего не делать?

С античных времен идея пустого пространства, находящегося на полпути между вещью и невещью, беспокоила философов. Сам Демокрит, сделавший пустое пространство основой своего мира, где движутся атомы, тоже, конечно, был далек от полной ясности по этому вопросу. Он писал, что пустое пространство – это нечто «между бытием и небытием»: «Демокрит… считал первоначалами полное и пустое, называя одно “существующим”, а другое “несуществующим”», – пишет Симпликий. Атомы – это существующее. Пространство – «несуществующее», которое, тем не менее, существует. Трудно высказаться более неопределенно.

Ньютон, реанимировавший демокритовскую идею пространства, пытался исправить положение, утверждая, что пространство – это сенсориум Бога. Никто никогда не понимал, что подразумевал Ньютон под «сенсориумом Бога», – возможно, и сам Ньютон тоже. И конечно, Эйнштейн, считавший идею Бога (с сенсориумом или без него) полезной лишь в качестве шутливого риторического приема, находил ньютоновское объяснение природы пространства крайне неубедительным.

Ньютон прикладывал значительные усилия к тому, чтобы преодолеть сопротивление ученых и философов реанимируемой им демокритовской концепции пространства, но поначалу никто не хотел воспринимать его всерьез. Лишь поразительная эффективность его уравнений, с помощью которых, как оказалось, всегда можно делать корректные предсказания, положила конец глухому недовольству. Тем не менее сомнения в правдоподобности ньютоновского представления о пространстве остались, и Эйнштейн, который читал труды философов, хорошо об этом знал. Концептуальные трудности ньютоновской идеи пространства подчеркивал Эрнст Мах, философ, влияние которого Эйнштейн открыто признавал, – тот самый Мах, который не верил в существование атомов. (Между прочим, это хороший пример того, как один и тот же человек может проявлять близорукость в одном отношении и прозорливость в другом.)

Таким образом, Эйнштейн взялся не за одну, а сразу за две проблемы. Первая: как описывать гравитационное поле? Вторая: что такое ньютоновское пространство?

И тут Эйнштейну пришла в голову гениальная идея – это был один из величайших взлетов мысли в истории: а что, если гравитационное поле в действительности и есть загадочное ньютоновское пространство? Что, если ньютоновское пространство не что иное, как гравитационное поле? Эта чрезвычайно простая, красивая, блестящая идея и составляет суть общей теории относительности.

Состав мира – это не пространство + частицы + электромагнитное поле + гравитационное поле. Состав мира – это просто частицы + поля и ничего больше; нет необходимости добавлять пространство в качестве отдельного ингредиента. Ньютоновское пространство – это гравитационное поле. Или наоборот (что не меняет смысла): гравитационное поле – это пространство (рис. 3.5).

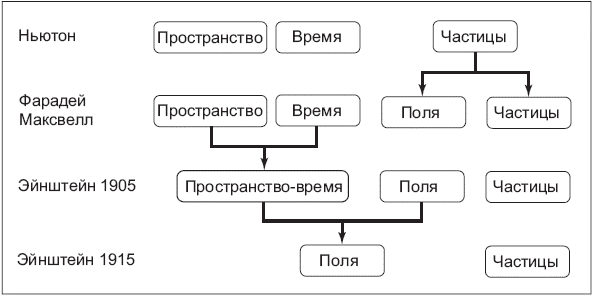
Рис. 3.5. Из чего состоит мир?

Но в отличие от ньютоновского пространства, плоского и неподвижного, гравитационное поле, в силу того что оно является полем, есть нечто движущееся и колеблющееся в соответствии со своими уравнениями подобно максвелловскому полю и фарадеевым линиям.

Картина мира радикально упрощается. Пространство больше не отличается от материи. Это одна из материальных составляющих мира подобно электромагнитному полю. Это реальная сущность, которая колеблется, флуктуирует, гнется и мнется.

Рис. 3.6. Земля обращается вокруг Солнца, потому что пространство-время вокруг Солнца искривлено, она подобна горошине, которая кружится в воронке

Мы больше не привязаны к невидимым жестким подмосткам – мы погружены в тело гигантского гибкого моллюска (метафора Эйнштейна). Солнце искривляет пространство вокруг себя, а Земля не обращается вокруг него под влиянием таинственной действующей на расстоянии силы, а движется прямо по покатому пространству. Она подобна горошине, которая кружится в воронке: нет никакой загадочный силы, создаваемой центром воронки, просто кривизна стенок заставляет горошину двигаться по окружности. Планеты обращаются вокруг Солнца, а вещи падают, поскольку пространство вокруг них искривлено (рис. 3.6).

Если быть немного точнее, то искривляется не пространство, а пространство-время – то самое пространство-время, которое, как десятью годами ранее показал сам Эйнштейн, представляет собой единую структуру, а не последовательность мгновений.

Такова идея. Единственной задачей Эйнштейна было найти уравнения, которые придадут ей прочность. Как описать это искривляющееся пространство-время? И здесь Эйнштейну повезло: проблема уже была решена математиками.

Величайший математик XIX столетия Карл Фридрих Гаусс, которого называли королем математиков, разработал метод математического описания искривленных поверхностей – холмистых ландшафтов вроде тех, что изображены на рис. 3.7.

Рис. 3.7. Искривленная (двумерная) поверхность

Затем он попросил одного своего талантливого студента обобщить этот подход на искривленные пространства в трех и более измерениях. Этот студент, Бернхард Риман, подготовил обширную диссертацию, которая казалась совершенно бесполезной.

Полученный Риманом результат заключался в том, что свойства искривленного пространства (или пространства-времени) любой размерности описываются определенным математическим объектом, который мы сегодня называем римановской кривизной и обозначаем буквой R. Если представить себе равнинный, холмистый и горный ландшафты, то кривизна R поверхности равна нулю на равнинах, которые являются плоскими («без кривизны»), и отлична от нуля на холмах и в долинах; она достигает максимума на острых горных пиках, то есть там, где поверхность дальше всего от плоской, сильнее всего искривлена. С помощью римановской теории можно описывать форму кривых поверхностей в трех или четырех измерениях.

С огромным трудом, обращаясь за помощью к друзьям, лучше разбирающимся в математике, Эйнштейн освоил теорию Римана и записал уравнение, в котором кривизна R пропорциональна энергии материи. В словесной форме это уравнение можно выразить так: пространство-время сильнее искривляется там, где находится материя. И всё. Это уравнение аналогично уравнениям Максвелла, но применительно к гравитации, а не к электричеству. Оно занимает полстроки, и ничего больше не требуется. Образное представление об искривленном пространстве выражается в этом уравнении.

Внутри этого уравнения заключена целая текучая вселенная. В нем магическая сила теории раскрывается в фантасмагорическом ряду предсказаний, напоминающих бредовые видения сумасшедшего, которые, однако, оказываются истиной. Вплоть до самого начала 1980-х годов почти никто не принимал всерьез большую часть этих фантастических предсказаний. И все же, одно за другим, они подтверждались на опыте. Рассмотрим некоторые из них.

Для начала Эйнштейн вычисляет влияние массы, такой как Солнце, на кривизну окружающего пространства, а затем влияние этой кривизны на движение планет. Он находит, что движение планет соответствует предсказаниям уравнений Кеплера и Ньютона, но не совсем точно: вблизи Солнца влияние кривизны пространства сильнее, чем действие ньютоновской силы. Эйнштейн рассчитывает движение Меркурия, ближайшей к Солнцу планеты, для которой расхождение между его теорией и теорией Ньютона должно быть наибольшим, и находит различие: ближайшая к Солнцу точка орбиты Меркурия смещается каждый год на 0,43 секунды дуги больше, чем предсказывает теория Ньютона. Это очень маленькое различие, но астрономы могли его измерить, и результат сравнения предсказаний с астрономическими наблюдениями был однозначен: Меркурий движется по траектории, предсказанной Эйнштейном, а не Ньютоном. Меркурий, быстроногий посланец богов в крылатых сандалиях, следует за Эйнштейном, а не за Ньютоном.

Таким образом, уравнение Эйнштейна описывает, как искривляется пространство в непосредственной близости от звезды. Из-за этой кривизны свет отклоняется от своей траектории. Эйнштейн предсказывает, что Солнце вызывает искривление проходящего рядом с ним света. В 1919 году производится измерение; полученная величина отклонения света в точности соответствует предсказанию.

Однако искривляется не только пространство, но также и время. Эйнштейн предсказывает, что на Земле время течет быстрее на большей высоте и медленнее – на меньшей. Производится измерение, которое подтверждает этот факт. Сегодня во многих лабораториях есть чрезвычайно точные часы, и этот странный эффект может быть измерен даже для разницы высот всего в несколько сантиметров. Поместите одни часы на пол, а другие на стол, и те, что на полу, покажут, что прошло меньше времени, чем на столе. Почему? Потому что время не универсально и однозначно, оно способно растягиваться и сжиматься под влиянием близко расположенных масс. Земля, как и любая масса, искривляет пространство-время, замедляя течение времени в окружающем ее пространстве. Два близнеца, один из которых живет на уровне моря, а другой в горах, при встрече обнаружат, что один из них старше другого, хотя и совсем ненамного (рис. 3.8).

Рис. 3.8. Двое близнецов провели жизнь в разных местах: один на уровне моря, а другой – в горах. Когда они встретились, тот, кто жил в горах, оказался старше. Так проявляется гравитационное растяжение времени

Этот эффект дает интересное объяснение падению предметов. Если нарисовать на карте мира маршрут, по которому самолет летит из Рима в Нью-Йорк, он не будет выглядеть прямым: самолет описывает дугу, отклоняясь к северу. Почему? Поскольку поверхность Земли искривлена, путь, отклоняющийся к северу, короче, чем проложенный вдоль параллели. Расстояние между меридианами тем меньше, чем севернее вы находитесь; поэтому для сокращения пути лучше отклониться к северу (рис. 3.9).

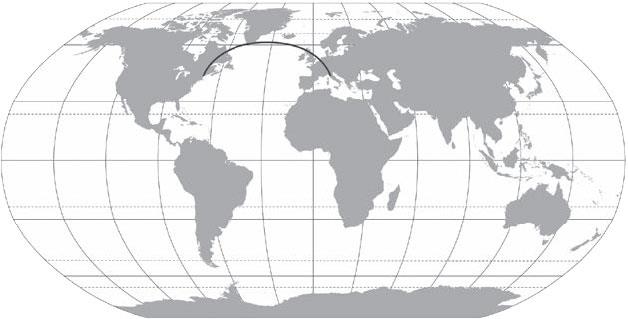
Рис. 3.9. Чем севернее вы находитесь, тем меньше расстояние между двумя меридианами

Так вот, верите вы в это или нет, но брошенный вверх мяч падает вниз по той же самой причине: он «выигрывает время», двигаясь вверх, поскольку время течет там с другой скоростью. В обоих случаях аэроплан и мяч следуют по прямым траекториям в искривленном пространстве (или пространстве-времени) (рис. 3.10).

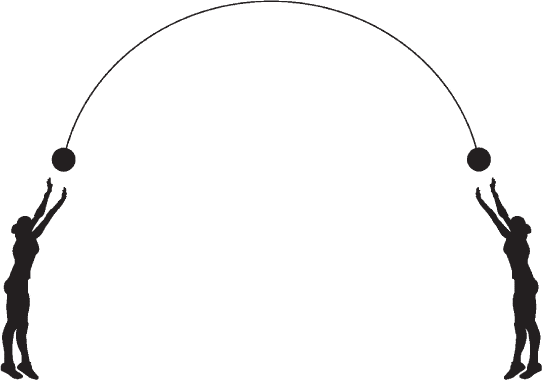
Рис. 3.10. Чем выше находится предмет, тем быстрее течет для него время

Однако предсказания теории идут гораздо дальше этих незначительных эффектов. Звезды горят столько времени, на сколько хватает им запасов водорода – их топлива, затем они умирают. Оставшееся вещество больше не поддерживается тепловым давлением и коллапсирует под собственным весом. Когда это происходит с достаточно большой звездой, вес оказывается так велик, что материя сжимается до колоссальной плотности, а пространство искривляется настолько сильно, что в нем образуется настоящая дыра. Черная дыра.

Когда я был студентом университета, черные дыры рассматривались как маловероятные следствия экзотической теории. Сегодня они наблюдаются сотнями и подробно изучаются астрономами. Одна из таких черных дыр с массой в миллион раз больше Солнечной системы расположена в центре нашей Галактики. Мы наблюдаем звезды, обращающиеся вокруг нее.

Некоторые из них, проходя слишком близко, разрушаются ее страшной гравитацией.

Далее, теория предсказывает, что пространство покрыто рябью подобно поверхности моря и что волны этой ряби подобны электромагнитным волнам, которые сделали возможным телевидение. Эффекты, связанные с этими гравитационными волнами, можно наблюдать в небе на двойных звездах: они испускают такие волны, теряя энергию и медленно падая друг на друга. Гравитационные волны, порожденные двумя падающими друг на друга черными дырами, непосредственно наблюдались с помощью антенны, установленной на земле в конце 2015 года. Об этом объявили в начале 2016 года, и мир вновь был ошеломлен. Еще раз безумное, казалось бы, предсказание теории Эйнштейна оказалось безупречно точным.

И это еще не всё: теория говорит, что Вселенная расширяется и возникла в космическом взрыве 14 миллиардов лет назад – об этом я вскоре расскажу подробнее.

Этот богатый и сложный набор явлений: отклонение лучей света, модификация ньютоновской силы, замедление часов, черные дыры, гравитационные волны, расширение Вселенной, Большой взрыв – вытекает из понимания того, что пространство – это не скучное неподвижное вместилище; оно обладает собственной динамикой и собственной физикой подобно материи и другим полям, которые в нем содержатся. Сам Демокрит непременно обрадовался бы, узнай он, что его идею пространства ждет такое впечатляющее будущее. Да, он называл его несуществующим, но то, что он считал существующим (δέν), было материей; и он писал, что это его «несуществующее», пустота, тем не менее «имеет некоторую природу (ϕύσιν) и самостоятельное бытие». Насколько же он был прав!

Без понятия поля, введенного Фарадеем, без впечатляющей силы математики, без геометрии Гаусса и Римана эта «некоторая собственная физика» так и оставалась бы непроясненной. Вооружившись новыми концептуальными средствами и математикой, Эйнштейн записал уравнения, которые описывают демокритовскую пустоту, и обнаружил, что ее «некоторая собственная физика» – это красочный и удивительный мир, где вселенные взрываются, пространство коллапсирует в бездонные дыры, время замедляется вблизи планет, а неограниченно расширяющееся межзвездное пространство волнуется и колышется, как поверхность моря…

Всё это звучит как история, рассказанная безумцем, как пустые слова, которые ничего не значат. И всё же это – взгляд на реальность. Или лучше сказать, проблеск реальности, чуть менее смазанный, чем наш мутный и банальный повседневный ее образ. Реальность, которая кажется сделанной из той же ткани, что наши сны, но которая, тем не менее, более реальна, чем наши туманные фантазии.

И всё это – результат одной элементарной догадки о том, что пространство-время и гравитационное поле есть одно и то же, и одного простого уравнения, которое я обязан здесь воспроизвести, хотя большинство моих читателей, конечно, не сможет его расшифровать. Тем не менее я делаю это в надежде на то, что читатели смогут уловить отблеск его великолепной простоты:

В 1915 году изображение было еще проще, поскольку не было члена +Λg_ab, который Эйнштейн добавил двумя годами позже (и который я объясняю далее). R_ab зависит от римановской кривизны и вместе с 1/2g_ab представляет кривизну пространства-времени; T_ab означает энергию материи; G – та же константа, что и у Ньютона: постоянная, определяющая силу гравитационного взаимодействия.

Вот и всё. Идея и уравнение.

Прежде чем продолжить говорить о физике, я хотел бы сделать несколько замечаний о математике. Эйнштейн не был великим математиком. Он сам признавал, что испытывает трудности с математикой. В 1943 году он так ответил на вопрос девятилетней девочки по имени Барбара, которая написала ему о своих трудностях с этим предметом: «Не беспокойся о трудностях, возникающих с математикой, я могу тебя заверить, что мои собственные проблемы [с ней] еще серьезнее!» Это кажется шуткой, но Эйнштейн не шутил. С математикой ему требовалась помощь и разъяснения терпеливых однокурсников и друзей, таких как Марсель Гроссман. Феноменальной была именно его интуиция как физика.

В тот год, когда Эйнштейн завершал создание своей теории, он обнаружил, что соперничает с Давидом Гильбертом, одним из величайших математиков всех времен. По приглашению Гильберта Эйнштейн прочел лекцию в Гёттингене. Гильберт мгновенно понял, что Эйнштейн находится на пороге большого открытия, ухватил основную идею и попытался обойти Эйнштейна, чтобы первым записать правильные уравнения новой теории, над которой Эйнштейн работал достаточно медленно. Финишный рывок двух гигантов мысли был захватывающим состязанием, и на завершающей стадии счет шел буквально на дни. Эйнштейн в этот период выступал с публичными лекциями в Берлине почти каждую неделю и каждый раз представлял новое уравнение, волнуясь, как бы Гильберт не получил решение раньше. Но каждый раз уравнение оказывалось неверным. Пока, наконец, Эйнштейн не нашел правильное уравнение, лишь чисто символически опередив Гильберта. Но все же именно он выиграл эту гонку.

Гильберт как джентльмен никогда не ставил под вопрос победу Эйнштейна, хотя сам работал тогда над очень похожими уравнениями. Ему принадлежит мягкое и красивое высказывание, которое очень точно характеризует сложные отношение Эйнштейна с математикой и, возможно, сложные отношения между физикой и математикой в целом. Необходимым для построения теории относительности разделом математики была геометрия четырехмерного пространства, и Гильберт писал:

Почему? Потому что Эйнштейн обладал уникальной способностью представлять себе, как устроен мир, «видеть» его мысленным взором. Уравнения приходили к нему позже; они были языком, с помощью которого он переносил свои образы в реальность. Для Эйнштейна общая теория относительности не набор уравнений, это мысленный образ мира, с большим трудом переведенный на язык уравнений.

Главная идея теории состоит в том, что пространство-время искривляется. Если бы пространство-время имело только два измерения и мы жили бы на некоем подобии плоскости, то было бы нетрудно представить себе, что означают слова «физическое пространство искривляется». Это означало бы, что физическое пространство, в котором мы живем, не такое, как плоский стол, а напоминает поверхность с горами и долинами. Но мир, в котором мы обитаем, имеет не два измерения, а три. На самом деле даже четыре, если учитывать время. Представить себе искривленное пространство в четырех измерениях намного труднее, поскольку наше обыденное восприятие не создает у нас интуитивного ощущения объемлющего пространства, внутри которого искривляется пространство-время. Однако воображение Эйнштейна не испытывало трудности с интуитивным восприятием космического моллюска, в тело которого все мы погружены и который может сжиматься, растягиваться и перекручиваться, порождая пространство вокруг нас. Именно благодаря ясности этого образа Эйнштейн смог первым сформулировать свою теорию.

В самом конце между Гильбертом и Эйнштейном возникло некоторое напряжение. За несколько дней до того, как Эйнштейн опубликовал свое правильное уравнение, Гильберт отправил в журнал статью, в которой показывал, как близко он подошел к тому же решению. По сей день историки науки испытывают сомнения, оценивая соотношение вкладов этих двух гигантов. В какой-то момент их отношения охладились, Эйнштейн боялся, что Гильберт, который был старше и опытнее, станет приписывать себе основные заслуги в создании теории. Однако Гильберт никогда не говорил, что первым открыл общую теорию относительности, и в научном мире, где часто (даже слишком часто) возникают губительные споры о приоритете, эти двое дают поистине замечательный пример мудрости, очищающей научное поле от ненужного напряжения.

Эйнштейн пишет Гильберту замечательное письмо, в котором выражает глубокие чувства по поводу совместно пройденного пути:

Спустя два года после публикации своих уравнений Эйнштейн решает использовать их для описания пространства всей Вселенной, рассматриваемой в крупном масштабе. И здесь появляется еще одна из его замечательных идей.

Тысячи лет человек задавался вопросом: бесконечна Вселенная или у нее есть предел? Обе гипотезы влекут за собой серьезные проблемы. Бесконечность Вселенной, похоже, не выдерживает следующего рассуждения: если она бесконечна, значит, где-то должен существовать, например, читатель, абсолютно такой же, как вы, который читает эту же самую книгу (бесконечность поистине огромна, и не существует такого числа комбинаций атомов, чтобы заполнить ее объектами, всегда отличающимися друг от друга). Фактически должен существовать не один такой читатель, а бесконечное множество… Но если у Вселенной есть предел, то что же представляет собой ее граница? Как можно придать смысл границе, по другую сторону которой ничего нет? Еще в VI веке философ-пифагореец Архит Тарентский писал:

Кажется, что эти две абсурдные альтернативы – абсурд бесконечного пространства и абсурд Вселенной с фиксированной границей – не оставляет места для разумного выбора между ними.

Однако Эйнштейн находит третий путь: Вселенная может быть конечной и в то же время не иметь границы. Каким образом? Точно так же, как поверхность Земли не бесконечна, но не имеет границы, где бы она «кончалась». Подобное естественным образом происходит с искривленными вещами: поверхность Земли искривлена. И в общей теории относительности трехмерное пространство, конечно, может быть искривленным. Следовательно, наша Вселенная может быть конечной, но безграничной.

Если я буду все время идти по прямой линии на поверхности Земли, я не буду бесконечно удаляться, а в конце концов вернусь в ту точку, откуда вышел. Наша Вселенная может быть устроена подобным же образом: если я сяду на звездолет и буду все время лететь в одном направлении, я облечу Вселенную и в конце концов вернусь обратно на Землю. Трехмерное пространство такого типа – конечное, но безграничное – называется 3-сферой.

Для понимания геометрии 3-сферы обратимся к обычной сфере – поверхности мяча или Земли. Для изображения поверхности Земли на плоскости можно нарисовать два круга, как это обычно делают в случае карты мира (рис. 3.11).

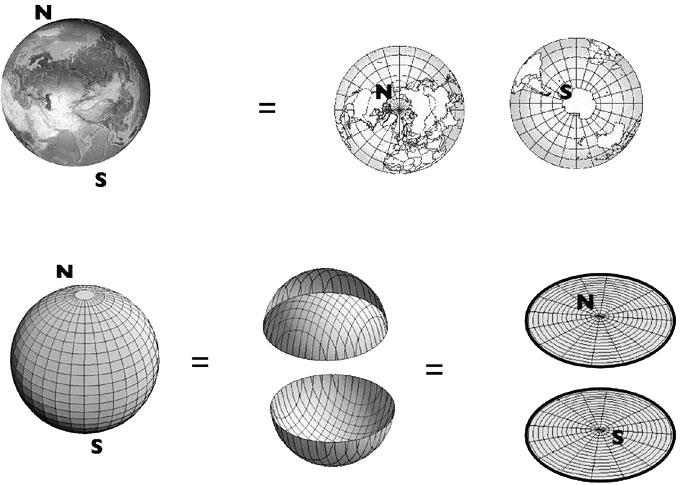
Рис. 3.11. Сферу можно изобразить в виде двух кругов, которые в действительности гладко соединяются друг с другом вдоль своих краев

Обратите внимание, что житель Южного полушария в некотором смысле окружен Северным полушарием, поскольку, в каком бы направлении ни покинул он свое полушарие, в результате он всегда попадет в другое. Но верно и обратное: каждое из полушарий окружает другое и окружено другим. Аналогичным образом можно представить себе и 3-сферу, но она рассматривается и в дополнительном измерении: два шара соединены друг с другом по всем своим границам (рис. 3.12).

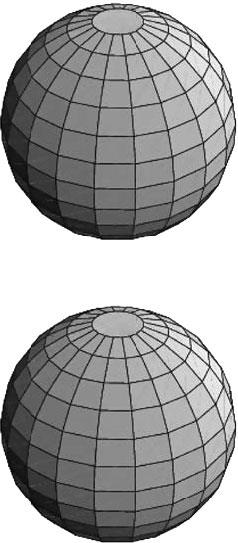
Рис. 3.12. 3-сферу можно представить в виде двух шаров, соединенных друг с другом

Покидая один шар, мы вступаем в другой, точно так же как, покидая один круг карты мира, мы попадаем в другой. Каждый из шаров окружает другой и окружен им. Идея Эйнштейна состоит в том, что пространство может быть 3-сферой – иметь конечный объем (равный сумме объемов двух шаров), но не иметь границ. В своей работе 1917 года Эйнштейн предложил 3-сферу в качестве решения проблемы границы Вселенной. С этой статьи начинается современная космология, изучение всей видимой Вселенной, рассматриваемой в самом крупном масштабе. Она порождает открытие расширения Вселенной, теорию Большого взрыва, проблему рождения Вселенной и еще много чего другого. Я подробнее расскажу обо всем этом в главе 8.

Есть еще одно замечание, которое я бы хотел сделать относительно эйнштейновской 3-сферы. Может показаться невероятным, но эта идея уже была предложена другим гением из совершенно иной культурной вселенной – великим итальянским поэтом Данте Алигьери. В «Рае», третьей части своей главной поэмы «Божественная комедия», Данте рисует величественный образ средневекового мира, уподобленный миру Аристотеля, со сферической Землей в центре, окруженной небесными сферами (рис. 3.13).

В сопровождении своей сияющей возлюбленной Беатриче, Данте в ходе фантастического мысленного путешествия поднимается по этим сферам до самой внешней сферы. Достигнув ее, он созерцает под собой мир с его вращающимися небесами и Землей далеко внизу в самом центре. Но затем он смотрит вверх – и что же он видит? Он видит светящуюся точку, окруженную огромными сферами ангелов, иными словами – другую колоссальную сферу, которая, по его словам, «окружает и в то же время окружена» сферой нашей Вселенной! Здесь в строках XXVII песни «Рая» он пишет: “Questa altre parte dell’Universo d’un cerchio lui comprende si come questo li altri”, а затем в XXX песни повторяет о последней точке: “parendo inchiuso da quell ch’elli inchiude”. Точка света и сфера ангелов окружают Вселенную, и в тоже время они окружены Вселенной! Это точное описание 3-сферы!

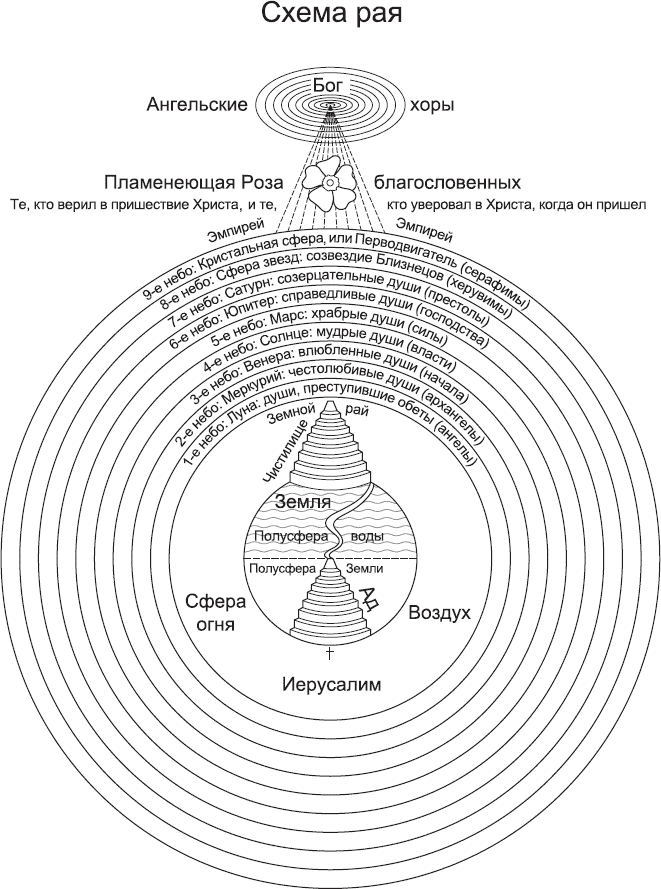
Рис. 3.13. Традиционное представление Вселенной Данте

Американский математик Марк Петерсон в 1979 году первым заметил, что «Рай» описывает Вселенную как 3-сферу. В целом исследователи творчества Данте не очень хорошо знакомы с 3-сферами. Однако любой современный физик или математик легко распознает 3-сферу в дантовском описании Вселенной.

Каким образом Данте могла прийти в голову идея, звучащая столь современно? Я думаю, это в первую очередь отражение глубочайшего интеллекта великого итальянского поэта. Именно его ум делает «Божественную комедию» такой восхитительной. Но также это связано с тем, что Данте писал задолго до того, как Ньютон убедил всех, что бесконечное пространство космоса имеет плоскую евклидову геометрию. Данте был свободен от ограничений, наложенных на нашу интуицию в результате ньютонианского обучения.

Научная культура Данте основывалась главным образом на поучениях его наставника Брунетто Латини, от которого до нас дошел небольшой очаровательный трактат «Li tresor», своего рода энциклопедия средневекового знания, написанная на дивной смеси старофранцузского и итальянского. В «Li tresor» Брунетто подробно объясняет, почему Земля является круглой.

Но он делает это странным для современного читателя способом – в категориях «внутренней», а не «внешней» геометрии. То есть он не пишет, что Земля похожа на апельсин, не говорит, как она выглядит, если смотреть на неё извне, а объясняет ее форму так: «Два рыцаря, которые достаточно далеко проскачут в противоположных направлениях, встретятся на противоположной стороне». И так: «Если бы не мешали моря, человек, начавший идти в одну сторону, вернулся бы в ту же точку Земли, откуда вышел». Иными словами, он использует внутреннюю, а не внешнюю точку зрения – с позиции того, кто идет по Земле, а не того, кто смотрит на нее со стороны. На первый взгляд, это может показаться бессмысленным, усложненным способом объяснения того, что Земля является шаром. Почему Брунетто просто не говорит, что Земля похожа на апельсин? Но с другой стороны, если мы скажем, что муравей ползет по апельсину, то в какой-то момент он окажется в перевернутом положении и должен будет удерживаться крошечными присосками на ногах, чтобы не упасть. Однако путешественник, идущий по Земле, никогда не оказывается в перевернутом положении и не нуждается в присосках на ногах. Так что описание Брунетто на самом деле не такое уж странное.

Теперь задумайтесь над этим. Некто узнал от своего учителя, что форма поверхности нашей планеты такова, что, двигаясь все время по прямой линии, мы возвращаемся в точку, откуда вышли. Вероятно, не так уж трудно сделать следующий очевидный вывод и осознать, что форма всей Вселенной такова, что, двигаясь все время по прямой линии, мы вернемся в ту же точку, из которой отправились: 3-сфера – это пространство, в котором «два крылатых рыцаря, способных лететь в противоположных направлениях, встретятся на противоположной стороне». Выражаясь более формально, описание геометрии Земли, предложенное Брунетто Латини в «Li tresor», дано в терминах внутренней геометрии (рассматриваемой изнутри), а не внешней (рассматриваемой снаружи), и это как раз такое описание, которое подходит для обобщения понятия сферы с двух измерений на три. Лучший способ описания 3-сферы – это не пытаться «увидеть ее снаружи», а описывать то, что происходит, когда вы движетесь внутри нее.

Метод, разработанный Гауссом для описания кривых поверхностей и обобщенный Риманом для описания искривления пространства в трех и более измерениях, в основе своей следует пути Брунетто Латини. Идея, можно сказать, состоит в том, чтобы описывать кривизну пространства не как «видимую со стороны», говоря, как оно искривляется во внешнем пространстве, а в тех понятиях, которые может воспринимать наблюдатель, находящийся внутри этого пространства и способный двигаться, всегда оставаясь в нем самом. Например, обычная сфера, как заметил Брунетто, – это такая поверхность, где все «прямые» линии возвращаются к исходной точке, пройдя одно и то же расстояние (длину экватора). 3-сфера – это трехмерное пространство, обладающее таким же свойством.

Эйнштейновское пространство-время искривлено не в том смысле, что оно изогнуто «во внешнем пространстве». Оно искривлено в том смысле, что его внутренняя геометрия, то есть сеть расстояний между его точками, которые можно измерять, оставаясь внутри него, не соответствует геометрии плоского пространства. Это пространство, где неверна теорема Пифагора точно так же, как она неверна на поверхности Земли.

Существует важный для понимания дальнейшего изложения способ убедиться в кривизне пространства изнутри него, не пытаясь взглянуть на него извне. Представьте себе, что вы находитесь на Северном полюсе и идете на юг, пока не достигнете экватора. При этом вы несете с собой стрелку, которая показывает вперед. Дойдя до экватора, вы поворачиваете налево, не меняя направление стрелки. Она по-прежнему показывает на юг, который теперь находится для вас справа. Пройдите немного на восток вдоль экватора, а затем поверните обратно на север, опять не меняя направление стрелки, которая теперь будет показывать назад. Когда вы вернетесь на Северный полюс, ваш маршрут замкнется, образовав петлю, но стрелка уже не будет показывать в том же направлении, что и при старте (рис. 3.14). Угол, на который повернулась стрелка при обходе петли, служит мерой кривизны.

Я еще вернусь к данному методу измерения кривизны с помощью петель в пространстве. Это будут петли, которые дали название теории петлевой квантовой гравитации.

Данте покидает Флоренцию в 1301 году, когда завершается изготовление мозаики купола Флорентийского баптистерия. Мозаика, изображавшая ад (работы Коппо ди Марковальдо, учителя Чимабуэ), вероятно, устрашавшая средневековых людей, часто упоминается как источник вдохновения Данте (рис. 3.15).

Я посетил баптистерий вскоре после начала работы над этой книгой в компании Эммануэлы Минней, которая убедила меня ее написать. Войдя в баптистерий и посмотрев вверх, я увидел сияющую точку света (свет исходит от фонаря на вершине купола), окруженную девятью ангельскими чинами с названиями, подписанными в следующем порядке: ангелы, архангелы, начала, власти, силы, господства, престолы, херувимы, серафимы. Это в точности соответствует структуре второй сферы рая. Вообразите себя муравьем на полу баптистерия, способным ползти в любую сторону; независимо от того, в каком направлении карабкаться по стене, вы достигнете потолка в одной и той же точке света, окруженной ангелами: точка света и ее ангелы одновременно окружают и окружены всем остальным убранством баптистерия (рис. 3.16).

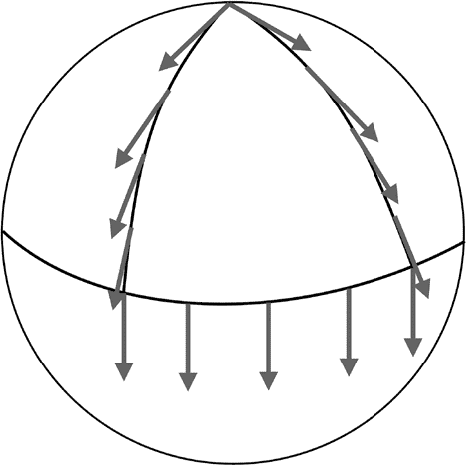
Рис. 3.14. Стрелка, сохраняющая параллельность самой себе при переносе вдоль замкнутого маршрута (петли), в искривленном пространстве возвращается к точке отправления повернутой

Рис. 3.15. Мозаика, изображающая ад, работы Коппо ди Марковальдо во Флорентийском баптистерии

Как и все жители Флоренции конца XIII века, Данте должен был быть преисполнен благоговейного трепета перед баптистерием, грандиозным архитектурным сооружением, возведенным его городом. Я думаю, что он мог вдохновляться баптистерием в своем видении космоса, причем не только «Адом» Коппо ди Марковальдо, но и всей архитектурой. «Рай» воспроизводит структуру баптистерия с замечательной точностью, включая девять кругов ангелов и точку света, только переносит ее из двух измерений в три. Описав сферическую Вселенную Аристотеля, Брунетто уже отмечает, что за ней лежит территория божественного, а средневековая иконография уже изображала рай как Бога, окруженного сферами ангелов. В конечном счете, Данте не более чем собрал все эти существовавшие фрагменты в согласованное архитектурное целое, следуя впечатляющей архитектуре баптистерия, и разрешил древнюю проблему границ Вселенной. Сделав это, Данте на шесть столетий опередил эйнштейновскую 3-сферу.

Рис. 3.16. Интерьер баптистерия

Я не знаю, сталкивался ли молодой Эйнштейн с «Раем» во время своих интеллектуальных странствий по Италии и оказало ли живое воображение итальянского поэта прямое влияние на его догадку о том, что Вселенная может быть одновременно конечной и безграничной. Но, независимо от возможности такого влияния, я считаю, что этот пример демонстрирует, как великая наука и великая поэзия способны давать нестандартный взгляд на вещи и даже приводить к одним и тем же догадкам. В нашей культуре наука и поэзия по какому-то недоразумению разделены, а ведь они обе открывают нам глаза на сложность и красоту мира.

Дантовская 3-сфера – это лишь образ из фантазии. Эйнштейновская 3-сфера имеет математическую форму и вытекает из уравнений теории. Влияние этих идей различно. Данте глубоко затрагивает источники наших эмоций. Эйнштейн открывает путь к нерешенным загадкам нашей Вселенной. Но каждый из них являет собой пример самого красивого и значительного полета человеческой мысли.

Но вернемся в 1917 год, когда Эйнштейн пытается включить представление о 3-сфере в свои уравнения. Здесь он сталкивается с проблемой. Он убежден, что Вселенная статична и неизменна, но его уравнения говорят, что это невозможно. Нетрудно понять почему. Все притягивается, а значит, для конечной Вселенной единственный способ избежать коллапса – расширяться. Точно так же, как единственный способ для футбольного мяча избежать падения на землю – получить удар, направленный вверх. Он либо летит вверх, либо падает вниз – он не может оставаться неподвижным, зависнув в воздухе.

Однако Эйнштейн не верит в то, что говорят ему собственные уравнения. Он даже допускает нелепую физическую ошибку (не понимает, что предложенное им решение является неустойчивым), лишь бы избежать принятия того, что предсказывает его теория: Вселенная либо сжимается, либо расширяется. Он модифицирует свои уравнения, пытаясь избежать вывода о расширении Вселенной. Именно с этой целью он добавляет в приведенное выше уравнение член Λg_ab. Но это новая ошибка: сам добавленный член корректен, но он не меняет того факта, что уравнение предсказывает расширение Вселенной. При всей смелости гению Эйнштейна не хватает храбрости поверить в собственные уравнения.

Спустя несколько лет Эйнштейн вынужден сдаться: верна его теория, а не его сомнения относительно нее. Астрономы обнаруживают, что все галактики действительно удаляются от нас – Вселенная расширяется, в точности как предсказывают уравнения. Около 14 миллиардов лет назад Вселенная была сконцентрирована в одной безумно горячей точке. Из нее Вселенная расширилась в колоссальном космическом взрыве. И здесь слово «космический» употреблено не риторически, а в буквальном смысле – это взрыв самого космоса, Большой взрыв.

Сегодня мы знаем, что расширение Вселенной – реальность. Убедительное подтверждение сценария, предсказанного уравнениями Эйнштейна, было получено в 1964 году, когда двое американских радиоастрономов, Арно Пензиас и Роберт Уилсон, случайно открыли излучение, заполняющее Вселенную; это излучение оказалось остатком того самого невероятного жара, который царил в молодой Вселенной. И снова теория оказалась верна в своих самых удивительных предсказаниях.

С тех пор как мы обнаружили, что Земля круглая и вертится, как безумный волчок, мы поняли, что реальность не такая, какой она окажется: всякий раз, когда мы схватываем новый ее аспект, мы испытываем глубокое эмоциональное переживание. Еще одна пелена спадает с наших глаз. Но шаг, сделанный Эйнштейном, беспрецедентен: пространство-время – это поле; мир состоит из полей и частиц; пространство и время – это не что-то иное, отличное от всей остальной природы, а просто одно из полей среди других (рис. 3.17).

Рис. 3.17. Эйнштейновский мир: частицы и поля, которые движутся по другим полям

В 1953 году ученик начальной школы пишет Альберту Эйнштейну: «Наш класс изучает Вселенную. Меня очень интересует пространство. Я хотел бы поблагодарить Вас за все, что Вы сделали, чтобы мы могли его понять».

Я полностью разделяю эти чувства.