Внимательный читатель заметит, что в предыдущих главах мало внимания уделялось времени. А ведь еще Эйнштейн более столетия назад показал, что нельзя разделять время и пространство, напротив, о них следует думать совместно, как о едином целом – пространстве-времени. Настал момент разобраться с этим и вернуть время в нашу картину мира.

Исследования по квантовой гравитации годами были сосредоточены на пространственных уравнениях, пока у ученых не хватило смелости взяться за время. За последние 15 лет стал формироваться способ понимания времени, который я постараюсь объяснить.

Пространство как аморфное вместилище вещей исчезает из физики с появлением квантовой гравитации. Вещи (кванты) не населяют пространство, но располагаются друг по отношению к другу, а пространство – это ткань их соседских отношений. И по аналогии с отказом от идеи пространства как пассивного вместилища мы должны отбросить идею времени как пассивного потока, вдоль которого развертывается реальность. Так же как исчезает идея пространственного континуума, содержащего вещи, должна исчезнуть и идея текущего континуума времени, в котором происходят все явления.

В некотором смысле в фундаментальной теории пространства больше не существует; кванты гравитационного поля не находятся в пространстве. В том же смысле в фундаментальной теории больше не существует времени: кванты гравитации не эволюционируют во времени. Время – это просто счетчик их взаимодействий. Как свидетельствует уравнение Уилера – Девитта, фундаментальные уравнения более не содержат временно́й переменной. Время, подобно пространству, появляется из квантового гравитационного поля.

Отчасти это уже есть в классической общей теории относительности, где время представляется проявлением гравитационного поля. Но пока мы пренебрегаем квантовой теорией, все еще можно думать о пространстве-времени довольно привычным образом – как о полотне, на котором разворачивается история всей остальной реальности, даже если это полотно динамичное и подвижное. В момент, когда мы принимаем в расчет квантовую механику, мы понимаем, что время тоже должно демонстрировать вероятностную неопределенность, зернистость и реляционность, которые присущи всей остальное реальности. Это делает время существенно отличным от всего, что мы подразумевали под этим словом прежде.

Это второе концептуальное следствие теории квантовой гравитации еще радикальнее, чем исчезновение пространства.

Попробуем в нем разобраться.

То, что природа времени отличается от общепринятых представлений, которые есть у всех нас, стало ясно уже более столетия назад. Специальная и общая теории относительности сделали это очевидным. Сегодня неадекватность нашего обыденного представления о времени можно легко продемонстрировать в лаборатории.

Рассмотрим, например, первое следствие общей теории относительности, описанное в главе 3. Возьмем двое часов, убедимся, что они показывают в точности одинаковое время, положим одни из них на пол, а другие – на стол. Подождем полчаса и снова поместим их рядом. Будут ли они по-прежнему показывать одно и то же время?

Как говорилось в главе 3, ответ будет отрицательный. Обычные наручные часы или те, что встроены в мобильный телефон, не обладают необходимой точностью, чтобы проверить этот факт. Однако в физических лабораториях по всему миру есть часы, имеющие точность, которая позволяет продемонстрировать возникающее расхождение: часы, оставленные на полу, идут медленнее, чем такие же часы, расположенные выше.

Почему? Потому что время не течет одинаково повсюду в мире. В некоторых местах его поток быстрее, в других – медленнее. Чем ближе к Земле, где гравитация сильнее, тем медленнее течет время. Помните близнецов из главы 3, чей возраст стал различаться в результате того, что один жил у моря, а другой в горах? Этот эффект ничтожен – выигрыш во времени, полученный за всю жизнь приморским жителем в сравнении с горцем, составляет доли секунды, – однако столь малая величина не меняет того факта, что это реальное различие. Время ведет себя не так, как мы привыкли себе представлять.

Мы не должны думать о времени так, словно где-то существуют великие космические часы, которые отмеряют жизнь Вселенной. Уже более 100 лет мы знаем, что о времени следует думать как о локальном явлении: каждый объект во Вселенной имеет свое собственное время, темп которого определяется локальным гравитационным полем.

Но даже это представление о локальном времени перестает работать, когда мы принимаем в расчет квантовую природу гравитационного поля. Квантовые события в планковском масштабе больше не упорядочены ходом времени. Время, в некотором смысле, перестает существовать.

Что означают слова о том, что времени не существует?

Прежде всего, отсутствие временно́й переменной в фундаментальных уравнениях не означает, что всё становится неподвижным и что перестают происходить какие-либо изменения. Напротив, это означает, что изменения вездесущи. Вот только элементарные процессы не могут быть упорядочены вдоль привычной последовательности мгновений. В предельно малых масштабах, соответствующих квантам пространства, танец природы не подчиняется ритму, задаваемому одной дирижерской палочкой для всего оркестра: каждый процесс танцует независимо от соседей, следуя своему собственному ритму. Течение времени – это внутреннее свойство мира, оно рождается самим миром из отношений между квантовыми событиями, которые и есть мир и которые сами порождают свое собственное время.

Фактически несуществование времени не означает ничего особенно сложного. Давайте попробуем это понять.

Время входит в большинство уравнений классической физики. Это переменная, обозначаемая буквой t. Уравнения говорят нам, как вещи меняются во времени. Если мы знаем, что случилось в прошлом, они позволяют нам предсказать будущее. Точнее, мы измеряем некоторые величины, например положение A объекта, угол B отклонения маятника, температуру C объекта, а физические уравнения говорят, как эти величины будут меняться во времени. Они предсказывают функции A (t), B (t), C (t) и т. д., которые описывают изменения этих величин с течением времени t.

Галилей был первым, кто понял, что движение объектов на земле может описываться уравнениями как функции времени A (t), B (t), C (t), и первым записал формулы для этих уравнений в явном виде. Например, первый закон земной физики, найденный Галилеем, описывал падение предмета, иначе говоря, показывал, как его высота x меняется с ходом времени t.

Для открытия и проверки этого закона Галилею потребовались два типа измерений. Он измерял высоту x предмета и время t. Поэтому ему был нужен инструмент для измерения времени – часы.

Во времена Галилея не было точных часов. Сам Галилей еще в молодости нашел способ изготовления точных хронометров. Он обнаружил, что колебания маятника всегда имеют одинаковую длительность (независимо от амплитуды). Поэтому можно измерять время, просто считая качание маятника. Эта идея кажется такой очевидной, но только Галилей обратил на нее внимание, до него она никому не приходила в голову. Так нередко бывает в науке.

Но на самом деле всё не так однозначно.

Согласно легенде, эта идея озарила Галерея в величественном Пизанском соборе, где он наблюдал за медленными покачиваниями гигантской люстры со свечами. (Легенда не соответствует действительности, поскольку люстра впервые закачалась там через много лет после смерти Галилея, но история всё равно хороша. И не исключено, что в те времена в соборе висело что-то другое.) Ученый наблюдал за этими колебаниями во время религиозной службы, которой он, очевидно, не был особенно поглощен, и замерял длительность каждого качания люстры, подсчитывая удары собственного пульса. С нарастающим волнением он обнаружил, что число ударов одинаково для каждого качания – оно не менялось, когда люстра замедлялась и раскачивалась с ничтожной амплитудой. Все колебания имели одинаковую длительность.

Эта история звучит замечательно, но если задуматься, она вызывает недоумение, и это недоумение ведет нас к самой сути проблемы времени. Откуда Галилей знал, что удары его собственного пульса происходят через равные отрезки времени?

Вскоре после Галилея доктора стали измерять пульс своих пациентов, используя часы, которые, в конечном счете, представляли собой не что иное, как маятник. Получается, что мы использовали пульс, чтобы удостовериться в регулярности качаний маятника, а затем с помощью маятника проверяли постоянство пульса. Не кажется ли вам, что здесь имеет место какой-то порочный круг? Что бы это значило?

В действительности мы никогда не измеряем время само по себе, мы всегда измеряем физические величины A, B, C… (колебания, пульс и множество других вещей) и сравниваем одну величину с другой, то есть, иными словами, мы измеряем функции A(B), B(C), C(A) и т. д. Мы можем подсчитать, сколько ударов пульса в каждом колебании, сколько колебаний приходится на каждое тиканье секундомера, сколько тиканий секундомера между ударами башенных часов…

Суть в том, что нам удобно представлять себе, что существует величина t – «истинное время», – которая лежит в основе всякого движения, даже если ее нельзя измерить непосредственно. Мы записываем уравнения для физических переменных относительно этой ненаблюдаемой величины t – уравнения, которые говорят нам, как вещи меняются с изменением t: например, сколько времени занимает каждое колебание и сколько длится удар пульса. Отсюда мы можем вывести, как величины меняются друг по отношению к другу – сколько ударов пульса приходится на одно колебание – и сравниваем эти предсказания с тем, что наблюдаем в мире. Если эти предсказания оказываются корректными, мы верим в то, что наша сложная схема верна, и в частности в полезность переменной времени t, даже если ее нельзя непосредственно измерить.

Иными словами, существование переменной времени – это удобное допущение, а не результат наблюдений.

Первым, кто всё это понял, был Ньютон: он догадался, что это эффективный подход, прояснил и развил данную схему. Ньютон открыто пишет в своей книге, что нельзя измерить истинное время t, но если предположить, что оно существует, то получается эффективная конструкция для описания природы.

Прояснив этот момент, мы можем вернуться к квантовой гравитации и к смыслу утверждения о том, что «времени не существует». Это попросту означает, что ньютоновская схема перестает работать, когда мы имеем дело с очень маленькими вещами. Она была хороша, но только для больших вещей.

Если мы хотим добиться глубокого понимания мира, если хотим понять, как он функционирует в менее знакомых нам ситуациях, в которых становится существенной квантовая гравитация, нам придется отказаться от этой схемы. Представление о времени t, которое течет само по себе и по отношению к которому эволюционируют вещи, перестает быть полезным. Мир не описывается уравнениями эволюции во времени t. Мы должны просто перечислить переменные A, B, C, …, которые мы действительно наблюдаем, и записать уравнения, выражающие отношения между этими переменными и ничем больше: то есть уравнения для отношений A (B), B (C), C (A)…, которые мы наблюдаем, а не для функций A (t), B (t), C (t)…, которые мы не наблюдаем.

В примере с пульсом и люстрой у нас вместо происходящих во времени пульса и качаний люстры будут только уравнения, которые описывают, как две соответствующие им величины меняются друг по отношению к другу, то есть уравнение, которое прямо говорит нам, сколько ударов пульса приходится на одно качание люстры без упоминания t.

«Физика без времени» – это физика, в которой мы говорим только о пульсе и люстре, не упоминая о времени.

Это простое изменение, но с концептуальной точки зрения – это огромный скачок. Мы должны научиться думать о мире не как о чем-то изменяющемся во времени, но неким иным способом. Вещи меняются только по отношению друг к другу. На фундаментальном уровне времени не существует. Наше обыденное чувство течения времени есть лишь приближение, которое верно для наших макроскопических масштабов. Оно возникает в силу того, что мы воспринимаем мир в очень загрубленном, крупнозернистом виде.

Таким образом, мир, описываемый этой теорией, очень далек от того, что нам привычно. Больше не существует пространства, которое вмещает мир, и не существует времени, в течение которого происходят события. Есть элементарные процессы, в которых кванты пространства и материи непрерывно взаимодействуют друг с другом. Эту картину мира можно сравнить с чистым и спокойным альпийским озером, которое состоит из мириад быстро танцующих крошечных молекул воды. Иллюзия, будто мы окружены непрерывным пространством и временем, есть результат рассматривания издали плотного роя элементарных процессов.

Как эти общие идеи применяются к квантовой гравитации? Как описывать изменения без использования идеи пространства как контейнера и времени, вдоль которого скользит мир?

Рассмотрим процесс, например, столкновения двух бильярдных шаров на столе, обтянутом зеленым сукном. Пусть красным шаром бьют по желтому; он приближается, ударяется, и два шара разлетаются в разных направлениях. Этот процесс, как и все процессы, происходит в конечной области пространства (скажем, на столе шириной около двух метров) и длится конечное время (допустим, три секунды). Чтобы обсуждать этот процесс в контексте квантовой гравитации, необходимо включить пространство и время в сам этот процесс (рис. 7.1).

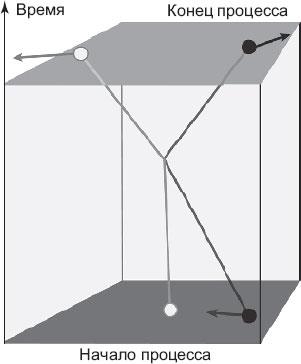
Рис. 7.1. Область пространства, в которой черный шар ударяет покоящийся белый шар, заставляя его двигаться, и отскакивает. Коробка – это область пространства-времени. Внутри нее нарисованы траектории шаров

Иными словами, мы должны описывать не только два шара, но также все, что находится вокруг них: стол и любые другие материальные объекты, а также пространство, в которое они погружены в течение времени, которое прошло между начальным ударом и концом процесса. Пространство и время – это гравитационное поле, эйнштейновский «моллюск»: мы также включаем в процесс гравитационное поле, то есть кусок этого моллюска. Все погружено внутрь этого огромного эйнштейновского моллюска. Теперь представьте, что вы отрезаете от него небольшой, конечный кусочек наподобие суши, который включает столкновение и то, что его окружает.

В результате мы получаем пространственно-временную коробку (как на рис. 7.1) – конечную порцию пространства-времени объемом несколько кубометров в пространстве и несколько секунд во времени. Этот процесс не происходит во времени. Эта коробка не находится в пространстве-времени, она включает в себя пространство-время. Это не процесс во времени – в том же смысле, в каком зерна пространства не находятся в пространстве. Течение времени – это лишь мера самого процесса, так же как кванты гравитации не находятся в пространстве, а сами представляют собой пространство.

Ключ к пониманию того, как работает квантовая гравитация, лежит в рассмотрении не только физического процесса, заданного двумя шарами, но и целостного процесса, заданного всей коробкой, со всем, что в ней содержится, включая гравитационное поле.

Теперь вернемся к первоначальный догадке Гейзенберга: квантовая механика говорит нам не о том, что происходит во время протекания процесса, но о вероятности, которая связывает различные начальные и конечные состояния этого процесса. В нашем случае начальные и конечные состояния задаются всем, что происходит на границе пространственно-временной коробки.

Уравнения петлевой квантовой гравитации дают нам вероятность, связанную с заданной возможной границей коробки, – вероятность того, что шары покинут коробку в той или иной конкретной конфигурации, если они вошли в нее в определенной начальной конфигурации.

Как вычисляется эта вероятность? Вспомним фейнмановскую сумму по путям, которую я описывал, когда рассказывал о квантовой механике. Вероятности в квантовой гравитации вычисляются таким же способом – путем рассмотрения всех возможных «траекторий», имеющих те же граничные условия. Поскольку мы включаем в рассмотрение динамику пространства-времени, это означает рассмотрение всех возможных пространств-времён, имеющих такую же границу, как у нашей коробки.

Квантовая механика предполагает, что между начальной границей, через которую два шара входят в коробку, и конечной границей, где они выходят, нет ни определенного пространства-времени, ни определенных траекторий шаров. Имеется только квантовое «облако», в котором сосуществуют все возможные пространства-времена и все возможные траектории. Вероятность увидеть шары выходящими одним или другим способом можно рассчитать, суммируя по всем возможным пространствам-временам.

Если квантовое пространство имеет структуру спиновой сети, то какую структуру будет иметь пространство-время? На что похожи упомянутые пространства-времена, которые должны учитываться в расчетах?

Это должны быть истории спиновой сети. Представьте, что вы берете граф спиновой сети и двигаете его: каждый узел паутины прочертит линию, подобно шарам на рис. 7.1, а каждое ребро графа, двигаясь, рисует поверхность (например, движущийся отрезок рисует прямоугольник). Но есть и кое-что еще: узел может разделиться на два или более узла, так же как частица может распасться на две или более частицы. И наоборот, два или более узла могут объединиться в один. Таким образом, эволюционирующий граф порождает рисунок, подобный тому, что представлен на рис. 7.2.

Изображение, представленное справа на рис. 7.2, – это спиновая пена. Пена – потому что она состоит из поверхностей, которые встречаются вдоль линий, которые, в свою очередь, встречаются в вершинах, что напоминает пену из мыльных пузырей (рис. 7.3). Это спиновая пена – поскольку поверхности этой пены несут спины аналогично ребрам графа, эволюцию которых они описывают.

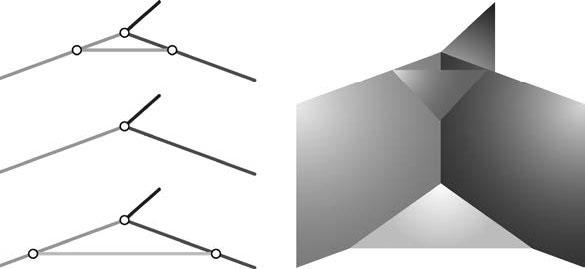
Рис. 7.2. Эволюционирующая спиновая сеть: три узла объединяются в один, а затем вновь разделяются. Справа – спиновая пена, представляющая этот процесс

Рис. 7.3. Пена из мыльных пузырей

Для расчета вероятности процесса надо просуммировать по всем возможным спиновым пенам внутри коробки, имеющим такую же границу, как в рассматриваемом процессе. Граница спиновой пены – это спиновая сеть с находящейся в ней материей.

Уравнения петлевой теории гравитации выражают вероятность процесса через суммы по спиновым пенам в заданных границах. На этом пути, в принципе, возможно вычислить вероятность любого физического события.

Рис. 7.4. Вершина спиновой пены. С разрешения Грэга Игана

На первый взгляд этот способ выполнения расчетов в квантовой гравитации, основанный на спиновой пене, кажется очень сильно отличающимся от обычных способов, которыми делаются вычисления в теоретической физике. Нет заданного пространства, нет заданного времени, а спиновая пена кажется объектом, чрезвычайно далеким от, скажем, частиц Стандартной модели. Однако в действительности есть очень сильное сходство между расчетами на основе спиновой пены и теми, что используются в Стандартной модели. Фактически здесь даже более чем сходство: техника спиновой пены – это на самом деле красивое объединение двух основных методов вычислений, используемых в контексте Стандартной модели – фейнмановских диаграмм и решетчатого приближения.

Фейнмановские диаграммы используются, например, для расчета процессов, в которых доминируют электромагнитные и слабые силы. Фейнмановская диаграмма представляет последовательность элементарных взаимодействий между частицами. На рис. 7.5 приведен пример, представляющий взаимодействия двух частиц или двух квантов поля. От левой частицы отделяются две другие частицы, одна из них, в свою очередь, распадается на две частицы, которые затем вновь объединяются и сливаются с правой частицей. Эта диаграмма изображает историю квантов в полях.

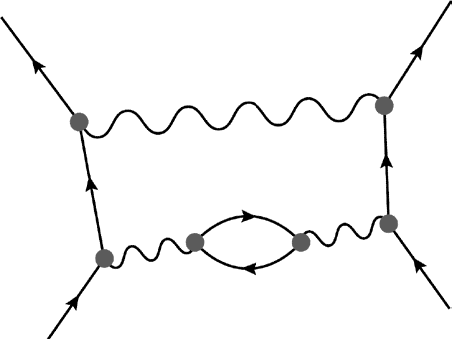
Рис. 7.5. Фейнмановская диаграмма

Решетчатое приближение используется, когда взаимодействие сильное и картина на уровне частиц становится неэффективной для описания физических процессов, например при расчете сильного взаимодействия между кварками внутри атомного ядра. Решетчатая техника строится на аппроксимации непрерывного физического пространства с помощью решетки, или сетки, как на рис. 7.6. Эта сетка рассматривается не как точное описание пространства, но лишь как приближение наподобие того, что используют инженеры, когда рассчитывают упругость моста, аппроксимируя свойства бетонных конструкций по методу конечных элементов. Эти два метода выполнения вычислений – фейнмановские диаграммы и решетка – самые эффективные техники в квантовой теории поля.

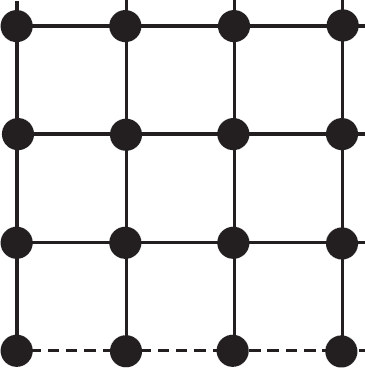
Рис 7.6. Сетка, аппроксимирующая физическое пространство-время

В квантовой гравитации происходит нечто очень красивое: эти два метода выполнения вычислений становятся одним и тем же. Пространственно-временная пена, изображенная на рис. 7.2 и используемая для расчета физических процессов в квантовой гравитации, может быть интерпретирована и как фейнмановская диаграмма, и как вычисление на решетке. Таким образом, эти две техники вычислений, используемые в Стандартной модели, оказываются частными случаями единой техники – суммирования по спиновой пене квантовой гравитации.

Ранее я уже представлял уравнения Эйнштейна. И вновь я не могу противиться искушению привести здесь полную систему уравнений петлевой теории, несмотря на то что читатель, очевидно, не сможет их расшифровать, если только не предпримет глубокое погружение в математику. Кто-то однажды сказал, что теория не заслуживает доверия, если ее уравнения нельзя записать на футболке. На рис. 7.7 представлена такая футболка с петлевой квантовой гравитацией.

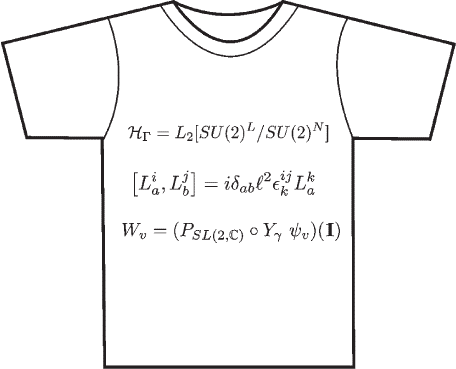
Рис. 7.7. Уравнения петлевой квантовой гравитации на футболке

Эти уравнения – математическая форма изложения картины мира, которую я описывал в последних двух главах. Мы вовсе не уверены в правильности этих уравнений, но, по моему мнению, это лучшая из имеющихся на сегодня формулировок квантовой гравитации.

Пространство – это спиновая сеть, узлы которой представляют его элементарные зерна, а ребра описывают их отношения близости. Пространство-время порождается процессами, в которых эти спиновые сети превращаются друг в друга, и эти процессы описываются суммами по спиновым сетям. Спиновая пена представляет историю спиновой сети, то есть зернистого пространства-времени, в котором узлы графа объединяются и разделяются.

Эти микроскопические роящиеся кванты, которые порождают пространство и время, лежат в основе окружающей нас безмятежной макроскопической реальности. Каждый кубический сантиметр пространства и каждая проходящая секунда есть порождение этой танцующий пены крошечных квантов.

Пространство как сцена исчезло, время исчезло, классические частицы исчезли, как и классические поля. Так из чего же состоит мир?

Ответ теперь прост: частицы – это кванты квантовых полей; свет образован квантами поля; пространство – это не более чем поле, которое также состоит из квантов; время появляется из процессов в тех же полях. Другими словами, мир целиком состоит из квантовых полей (рис. 7.8).

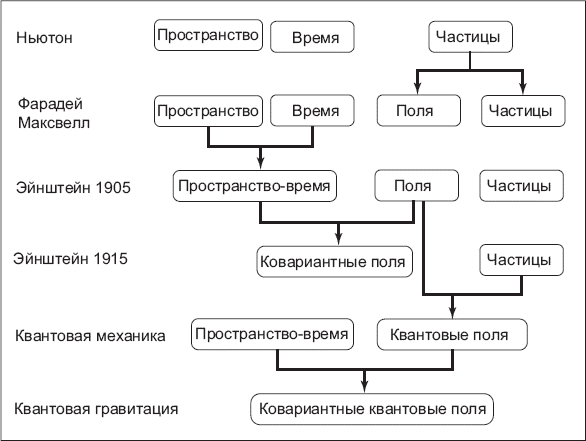
Рис. 7.8. Из чего состоит мир? Из одного-единственного ингредиента – ковариантных квантовых полей

Эти поля не живут в пространстве-времени; они, так сказать, просто живут: одно поверх другого – поля на полях. Пространство и время, которые мы воспринимаем в крупных масштабах, это наш размытый и приблизительный образ одного из этих квантовых полей – гравитационного поля.

Поля, которые живут сами по себе, не нуждаясь в пространстве-времени в качестве субстрата или опоры, и которые способны сами порождать пространство-время, называются ковариантными квантовыми полями. Сущность, составляющая наш мир, радикально упростилась за последние годы. Мир, частицы, свет, энергия, пространство и время – все это есть не что иное, как проявление одного-единственного типа сущностей – ковариантных квантовых полей.

Ковариантные квантовые поля стали сегодня лучшим описанием того, что мы можем назвать апейроном (ἄπειρον) – первичной субстанцией, из которой образовано все остальное. Это понятие выдвинул человек, который, вероятно, может быть назван первым ученым и первым философом, – Анаксимандр.

Граница между искривленным и непрерывным пространством эйнштейновской общей теории относительности и дискретными квантами квантовой механики, помещенными в плоское однородное пространство, исчезает. Кажущегося противоречия больше нет. Между континуумом пространства-времени и квантами пространства отношения такие же, как между электромагнитными волнами и фотонами. Волны дают приближенное крупномасштабное представление о фотонах. Фотоны – это способ, которым взаимодействуют волны. Непрерывные пространство и время – это крупномасштабный образ динамичных квантов гравитации. Кванты гравитации – это способ, которым взаимодействуют пространство и время. Одна и та же математика согласованно описывает квантовое гравитационное поле и другие квантовые поля.

Концептуальная цена, уплаченная за это, – отказ от традиционных идей пространства и времени в качестве общих структур, в рамки которых помещается мир. Пространство и время – это приближения, которые возникают лишь в крупных масштабах. Кант, по-видимому, был прав, утверждая, что субъект знания и его объект неразделимы, но он определенно ошибался, когда рассматривал ньютоновские пространство и время как априорные формы знания, неотъемлемые составляющие грамматики, необходимой для понимания мира. Эта грамматика изменилась и продолжает изменяться с ростом нашего знания.

Общая теория относительности и квантовая механика в конечном счете не настолько несовместимы, как это кажется. При тщательном рассмотрении они пожимают руки и замечательно вступают в диалог. Пространственные отношения, которые составляют суть эйнштейновского искривленного пространства, это ровно те же взаимодействия, которые составляют суть отношений между системами в квантовой механике. Две теории становятся совместимыми и объединяются подобно двум сторонам одной монеты, как только мы понимаем, что пространство и время – это проявления квантового поля и что квантовые поля могут существовать, даже не будучи помещенными во внешнее пространство.

Эта утонченная картина фундаментальной структуры физического мира и есть предлагаемый сегодня квантовой гравитацией новый взгляд на реальность.

Главное преимущество, которое дает эта физика, состоит, как мы увидим в следующей главе, в исчезновении бесконечностей. Бесконечно малого больше не существует. Бесконечности, портящие жизнь в квантовой теории поля, предпосылкой которых служит представление о непрерывном пространстве, теперь исчезают, поскольку они порождаются именно этим физически некорректным допущением о непрерывности пространства. Сингулярности, в которых уравнения Эйнштейна теряют смысл, когда гравитационное поле становится слишком сильным, тоже исчезают: они возникают лишь в результате пренебрежения квантованием поля. Шаг за шагом фрагменты пазла встают на свои места. В последней части книги я остановлюсь на некоторых физических следствиях этой теории.

Может показаться странным и трудным думать о дискретных элементарных сущностях вне пространства и времени, отношения которых, однако, составляют суть пространства и времени. Но представьте, насколько странно должны были звучать слова Анаксимандра, когда он утверждал, что под нашими ногами находится такое же небо, как то, что мы видим у себя над головой. Или слова Аристарха, который пытался измерить расстояние от Земли до Луны и Солнца и обнаружил, что они находятся чрезвычайно далеко, а значит, представляют собой не небольшие шары, а гигантские, и Солнце многократно превосходит размерами Землю. Или выводы Хаббла, когда он понял, что маленькие туманные облачка не звездном небе – это колоссальные скопления далеких звезд…

В течение столетий мир вокруг нас постоянно изменялся и расширялся. Теперь мы видим дальше, понимаем его лучше и поражаемся тому, как он трансформируется в зависимости от ограничений, наложенных на наше восприятие. Его описание, которое нам удается построить, становится все более изощренным, но одновременно более простым.

Мы подобны маленьким слепым кротам под землей, которые почти ничего не знают о мире. Но мы продолжает его изучать…