В самой глубине нашего понимания физического мира скрывается парадокс. Общая теория относительности и квантовая механика, эти два сокровища, которые оставил нам XX век, оказались щедрым подарком, способствующим пониманию мира и созданию современных технологий. Первое способствовало развитию космологии, а также астрофизики, изучению гравитационных волн и черных дыр. Второе обеспечило нас основами атомной и ядерной физики, физики элементарных частиц и конденсированного состояния, а также развитием многих других направлений.

И все же между этими двумя теориями есть серьезная коллизия. Они не могут быть верны вместе, по крайней мере не в их современной форме, поскольку они выглядят противоречащими друг другу. Гравитационное поле описывается без учета квантовой механики, без учета того факта, что поля являются квантовыми, а квантовая механика формулируется без учета того факта, что пространство-время искривляется и описывается уравнением Эйнштейна.

Для студента, слушающего по утрам курс общей теории относительности, а после обеда – лекции по квантовой механике, было бы простительно прийти к выводу, что читающие их профессора – дураки или что они не общались друг с другом как минимум столетие. По утрам мир представляет собой искривленное пространство-время, где всё непрерывно, а после обеда мир становится плоским и в нем взаимодействуют дискретные кванты энергетических скачков.

Парадокс состоит в том, что обе эти теории работают просто замечательно.

Во всех экспериментах и проверках природа продолжает говорить «да, вы правы» как общей теории относительности, так и квантовой механике, несмотря на очевидно противоположные допущения, на которых строятся эти две теории. Очевидно, что-то от нас ускользает.

В большинстве ситуаций мы можем пренебречь либо квантовой механикой, либо теорией относительности (либо ими обеими). Луна слишком велика и нечувствительна к крошечной квантовой зернистости, так что, описывая движение, можно забыть о квантах. С другой стороны, атом слишком легок, чтобы в значительной степени искривлять пространство, и, описывая его, можно забыть о кривизне пространства. Однако есть ситуации, когда важны и кривизна пространства, и квантовая зернистость, и для них у нас еще нет общепризнанной и работоспособной физической теории.

Одним из примеров могут служить внутренние области черных дыр. Другой пример – то, что случилось со Вселенной во время Большого взрыва. Иными словами, мы не знаем, как время и пространство ведут себя на очень малых масштабах. Во всех этих случаях современные теории начинают сбоить и больше не дают нам ничего разумного: квантовая механика не может работать с кривизной пространства-времени, а общая теория относительности не может учитывать кванты. Это и есть проблема квантовой гравитации.

Проблема даже глубже. Эйнштейн понимал, что пространство и время – это проявления физического поля, а именно гравитационного. Бор, Гейзенберг и Дирак понимали, что физические поля имеют квантовый характер: они зернисты, вероятностны, проявляются во взаимодействиях. Отсюда следует, что пространство и время также должны быть квантовыми сущностями, наделенными этими странными свойствами.

Что же такое квантовое пространство? Что такое квантовое время? Мы называем это проблемой квантовой гравитации. Команда физиков-теоретиков, разбросанных по пяти континентам, упорно трудится над ее разрешением. Их цель – не только найти теорию, то есть набор уравнений, но и выработать согласованную картину мира, которая позволит избавиться от нынешней шизофренической ситуации с квантами и гравитацией.

Это не первый случай, когда в физике имеются две очень успешные, но взаимно противоречащие друг другу теории. В прошлом усилия по синтезу таких теорий вознаграждались огромными прорывами в нашем понимании мира. Ньютон открыл закон всемирного тяготения, объединив галилееву физику, описывающую поведение вещей на земле, с кеплеровой физикой небесных явлений. Максвелл и Фарадей нашли уравнения электромагнетизма, объединив то, что было известно об электричестве, с тем, что было известно о магнетизме. Эйнштейн построил специальную теорию относительности, чтобы разрешить очевидный конфликт между ньютоновской механикой и максвелловским электромагнетизмом, а затем общую теорию относительности, чтобы разрешить конфликт, возникший между ньютоновской механикой и его собственной специальной теорией относительности.

Поэтому физики-теоретики только радуются, когда обнаруживают конфликт подобного типа, ведь он открывает исключительные возможности. Вопрос стоит так: можем ли мы сконструировать концептуальный каркас, совместимый с тем, что мы узнали о мире из обеих теорий?

Для понимания того, что такое квантовое пространство и квантовое время, нам надо еще раз глубоко пересмотреть наш способ восприятия окружающей действительности. Нужно заново осмыслить основы наших представлений о мире подобно тому, как это сделал Анаксимандр, который понял, что Земля висит в пространстве и что понятий «верх» и «низ» в космосе не существует, или подобно Копернику, который понял, что мы движемся по небесам с огромной скоростью, или подобно Эйнштейну, который догадался, что пространство-время деформируется, как моллюск, а время по-разному течет в разных местах… Еще раз повторю: в поисках целостной картины мира, сохраняющей то, что мы узнали о нем прежде, наши представления о природе реальности должны измениться.

Первым, кто осознал, что для понимания квантовой гравитации нам придется изменить концептуальный каркас, был романтический и легендарный персонаж – Матвей Бронштейн, молодой советский физик, живший и трагически погибший в сталинскую эпоху.

Рис. 5.1. Матвей Бронштейн

Матвей был другом Льва Ландау, ученого, которому предстояло стать лучшим физиком-теоретиком Советского Союза. Коллеги, знавшие их обоих, говорят, что талант Матвея был еще более ярким, чем у Льва. В то время, когда Гейзенберг и Дирак создавали основы квантовой механики, Ландау ошибочно полагал, что с квантами поле становится плохо определенным: квантовые флуктуации помешают измерять значения компонент поля в точках (сколь угодно малых областях) пространства. Проницательный Бор немедленно увидел, что Ландау ошибается, глубоко исследовал вопрос и написал большую подробную статью, в которой показывал, что поля, такие как электрическое, остаются хорошо определенными при использовании квантовой механики. Ландау отступил.

Однако его друг Матвей был заинтригован, поскольку понимал, что интуиция Ландау хотя и подвела его, говорила о чем-то очень важном. Он повторил те же рассуждения, с помощью которых продемонстрировал, что квантовое электрическое поле хорошо определено в точке пространства, применив их к гравитационному полю, для которого Эйнштейн лишь несколькими годами ранее записал уравнение. И тут – сюрприз! – Ландау оказался прав. Если принимать в расчет кванты, то гравитационное поле в точке не является хорошо определенным.

Есть интуитивный способ понять, о чем речь. Допустим, мы хотим наблюдать очень-очень-очень маленькую область пространства. Для этого необходимо поместить в эту область нечто, чтобы пометить точку, которую мы хотим рассматривать. Скажем, мы помещаем туда частицу. Гейзенберг понял, что нельзя долго локализовать частицу в точке пространства. Она вскоре переместится. Чем меньше область, в которой мы пытаемся локализовать частицу, тем больше скорость, с которой она улетает. (Это принцип неопределенности Гейзенберга.) Если частица улетает с большой скоростью, то она обладает большой энергией. Теперь примем в расчет теорию Эйнштейна. Энергия искривляет пространство. Большая энергия означает, что пространство сильно искривляется. Очень большое количество энергии в очень маленькой области искривляет пространство настолько сильно, что оно схлопывается в черную дыру, подобно коллапсирующей звезде. Но если частица проваливается в черную дыру, ее больше нельзя увидеть. Я не могу использовать ее как точку отсчета для области пространства. Таким образом, я не могу измерить сколь угодно малую область пространства, поскольку если я попробую это сделать, область исчезнет внутри черной дыры.

Это рассуждение можно сделать более точным, если добавить немного математики. Общий вывод: из совместного применения квантовой механики и общей теории относительности вытекает, что существует предел для делимости пространства. Масштабы меньше некоторого значения нам недоступны. Если точнее, там ничего не существует.

Насколько мала эта минимальная область пространства? Подсчитать несложно: нужно вычислить минимальный размер частицы перед ее падением в собственную черную дыру, и делается это вполне очевидным способом. Минимальная длина составляет около

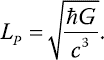
Под знаком квадратного корня располагаются три фундаментальные константы: ньютоновская постоянная тяготения G, обсуждавшаяся в главе 2, которая задает силу гравитации; скорость света c, введенная в главе 3 при рассмотрении теории относительности, которая открывает нам расширенное настоящее; и, наконец, постоянная Планка h, с которой мы познакомились в главе 4, определяющая масштаб квантовой зернистости. Присутствие этих трех констант подтверждает тот факт, что мы ищем нечто, связанное с гравитацией (G), теорией относительности (c) и квантовой механикой (h).

Расстояние L_P, определенное таким образом, называется планковской длиной. По справедливости следовало бы называть ее бронштейновской, но таков уж наш мир. Ее численное значение составляет примерно одну миллионную миллиардной миллиардной миллиардной доли сантиметра (10^–33 см). Так что она весьма мала.

Именно в таком экстремально малом масштабе проявляет себя квантовая гравитация. Чтобы получить представление, насколько мала обсуждаемая величина, представьте себе, что мы увеличили скорлупку грецкого ореха до размеров всей видимой Вселенной; но даже в таком масштабе планковская длина все еще не будет видна. Даже после такого колоссального увеличения она будет в миллион раз меньше ореха до увеличения. В этом масштабе пространство и время меняют свою природу. Они становятся чем-то совершенно иным – квантовыми пространством и временем, и понять, что это значит, довольно трудно.

Матвей Бронштейн понял все это в 1930-х годах и написал две короткие, но очень ясные статьи, в которых отмечал, что квантовая механика и общая теория относительности при совместном использовании несовместимы с нашим привычным представлением о пространстве как о бесконечно делимом континууме.

Вскоре, однако, возникла проблема. Матвей и Лев были искренними коммунистами. Они верили в революционное освобождение человечества, построение принципиально лучшего общества без несправедливости и без колоссального неравенства, которые, как мы видим, постоянно растут в мире. Они были твердыми последователями Ленина. Когда Сталин пришел к власти, это вызвало у них сначала растерянность, потом критическое отношение, затем враждебность. Они писали статьи, которые были умеренными, но открыто критичными… Это был не тот коммунизм, которого они хотели…

То были суровые времена. Ландау прошел через них; это было нелегко, но он выжил. Матвей же через год после того, как первым понял, что наши представления о пространстве и времени следует радикальным образом изменить, был арестован сталинскими спецслужбами и приговорен к смерти. Казнь состоялась в день вынесения приговора, 18 февраля 1938 года. Ему было всего 30 лет.

После безвременной кончины Матвея Бронштейна многие замечательные физики пытались разрешить загадку квантовой гравитации. Дирак посвятил этой проблеме последние годы своей жизни, открывая новые направления и вводя идеи и приемы, на которых строится значительная часть современных исследований в области квантовой гравитации. Именно благодаря этим приемам мы сегодня знаем, как описывать мир без времени, и в дальнейшем я об этом еще расскажу. Фейнман пытался адаптировать к общей теории относительности приемы, которые он разработал для электронов и протонов, но безуспешно: электроны и протоны – это кванты в пространстве, а квантовая гравитация – это нечто иное: недостаточно описать «гравитоны», движущиеся в пространстве, квантоваться должно само пространство.

Несколько Нобелевских премий были присуждены физикам, которым в ходе попыток распутать головоломку квантовой гравитации удалось почти по ошибке справиться с другими проблемами. Два голландских физика – Герард т’Хоофт и Мартинус Велтман – получили Нобелевскую премию в 1999 году за демонстрацию непротиворечивости теорий, которые используются сегодня для описания ядерных сил – части Стандартной модели, – но их исследовательская программа в действительности была нацелена на демонстрацию непротиворечивости теории квантовой гравитации. Их работа над теориями остальных сил была лишь подготовительным этапом. Этот «подготовительный этап» принес им Нобелевскую премию, но они не добились успеха в демонстрации непротиворечивости своей версии квантовой гравитации.

Если продолжить этот список, он станет похож на «доску почета» выдающихся физиков-теоретиков столетия. Или же перечень их неудач. Лишь постепенно, на протяжении десятилетий, идеи прояснялись, а тупиковые направления исследовались и закрывались; прояснялись технические приемы и общие идеи, начинали появляться результаты, выводимые один из другого. Чтобы только упомянуть здесь всех ученых, сделавших вклад в постепенное коллективное выстраивание этого направления науки, нам пришлось бы составить огромный список имен, в котором каждый добавил в общую работу свой камешек или булыжник.

Я бы хотел упомянуть только одного из них – того, кто много лет объединял различные направления этого коллективного исследования: замечательного, вечно молодого англичанина, философа и физика в одном лице – Криса Айшема. Именно читая его статью с обзором темы квантовой гравитации, я влюбился в эту проблему. Статья, по сути, объясняла, почему проблема столь сложна, как должны измениться наши представления о пространстве и времени, и давала четкий обзор всех путей, которые прослеживались на тот момент, с упоминанием достигнутых результатов и выявленных трудностей. Я был тогда студентом третьего курса, и возможность с нуля переосмыслить пространство и время привела меня в восхищение. Это восхищение с тех пор не ослабевало. И, как сказано в сонете Петрарки, «рана не проходит, когда теряет силу тетива».

Ученым, который внес наибольший вклад в квантовую гравитацию, был легендарный Джон Уилер, ставший связующим звеном для физики прошлого столетия. Ученик и коллега Нильса Бора в Копенгагене; коллега Эйнштейна после его переезда в Соединенные Штаты; учитель, среди учеников которого был, например, Ричард Фейнман… Уилер был сердцем физики XX века. Он был одарен ярким воображением. Именно он придумал и сделал популярным термин «черная дыра». Его имя связано с ранними широкими исследованиями – часто более интуитивными, нежели математическими, – вопроса о квантовом пространстве-времени. Восприняв урок Бронштейна о том, что квантовые свойства гравитационного поля влекут за собой изменения в представлениях о пространстве на малых масштабах, Уилер искал новые идеи, помогающие понять это квантовое пространство. Он представлял его облаком наложенных друг на друга геометрий, подобно тому как мы представляем квантовый электрон облаком его положений.

Рис. 5.2. Джон Уилер

Представьте, что вы смотрите на море с большой высоты: вы воспринимаете его огромную протяженность как плоский зеленоватый стол. Затем вы снижаетесь и смотрите на него с меньшего расстояния. Вы начинаете замечать огромные волны, гонимые ветром. Вы опускаетесь еще ниже и видите, что волны разбиваются, а поверхность моря покрыта беспорядочной пеной. Вот на что похоже пространство в представлении Уилера. В масштабах нашего восприятия, неимоверно превосходящих планковскую длину, пространство гладкое. Если же мы спустимся к планковскому масштабу, оно рвется и пенится.

Уилер искал способ описания пенящегося пространства, этой волны вероятности различных геометрий. В 1966 году его молодой коллега Брайс Девитт, живший в Каролине, нашел ключ к этой задаче. Уилер часто путешествовал и всюду, где мог, встречался с коллегами. Он попросил Брайса встретить его в аэропорту Рейли/Дюрхем в Северной Каролине, где ему предстояло несколько часов ждать пересадки. Приехав, Брайс показал ему уравнение для волновой функции пространства, полученное с использованием несложного математического приема. Уилер пришел в восторг. В этом разговоре родилось своего рода «уравнение для орбиталей» в общей теории относительности; уравнение, которое должно определять вероятность того или иного искривления пространства. Долгое время Девитт называл его уравнением Уилера, тогда как Уилер называл его уравнением Девитта. Теперь все называют его уравнением Уилера – Девитта.

Идея была очень удачной и легла в основание попыток построить полную теорию квантовой гравитации. Однако само это уравнение создает проблемы, причем серьезные. Прежде всего, с математической точки зрения уравнение действительно очень плохо определено. Если попытаться использовать его для вычислений, мы скоро получим бесконечные результаты, не имеющие смысла. Это требовалось исправить.

Вдобавок это уравнение трудно интерпретировать так, чтобы придать ему смысл. Среди его аспектов, приводящих в замешательство, можно назвать тот факт, что в уравнении не содержится переменной, обозначающей время. Как использовать его для расчетов эволюции чего-либо, происходящего во времени, если время в него вообще не входит? Уравнения динамики в физике всегда содержат переменную t, время. Что означает физическая теория без временно́й переменной? Годами исследователи будут биться над подобными вопросами, пытаясь различными способами пересмотреть уравнение, чтобы улучшить его определенность и понять, что оно означает.

Туман начал рассеиваться к концу 1980-х годов. Неожиданно появились некоторые решения уравнения Уилера – Девитта. В эти годы мне довелось встретиться в Сиракузском университете (штат Нью-Йорк) с индийским физиком Абэйем Аштекаром, а затем в Йельском университете с физиком Ли Смолином. Этот период запомнился мне интенсивными дискуссиями и жгучим интеллектуальным задором. Аштекар переписал уравнение Уилера – Девитта в более простой форме; Смолин совместно с Тедом Якобсоном из Мэрилендского университета в Вашингтоне был первым, кто нашел новые странные решения этого уравнения.

У этих решений была одна любопытная особенность: они зависели от замкнутых линий в пространстве. Замкнутая линия – это петля. Смолин и Якобсон смогли найти решение уравнения Уилера – Девитта для любой петли, то есть для любого замкнутого контура. Какое значение это имело? Первые работы в области, которая в дальнейшем стала называться петлевой квантовой гравитацией, появились из дискуссий, в ходе которых постепенно прояснялся смысл решений уравнения Уилера – Девитта. На этих решениях шаг за шагом стала воздвигаться целостная теория, унаследовавшая название «петлевая теория» от первых изученных решений.

Сегодня над этой теорией работают сотни исследователей, разбросанных по всему миру – от Китая до Аргентины, от Индонезии до США. То, что было постепенно выстроено, называется теперь петлевой теорией, или петлевой квантовой гравитацией, – ей посвящены следующие главы. Это не единственное направление, исследуемое в поисках квантовой теории гравитации, но я считаю его самым многообещающим.