12. Типичные регрессионные ошибки
Важное предупреждение

При проведении исследований, предполагающих выполнение регрессионного анализа, вы должны помнить одну очень важную вещь: постарайтесь никого не убить. Можете даже приклеить скотчем к монитору своего компьютера листочек с надписью: «Твои исследования не должны убивать людей». Дело в том, что подчас даже самые умные люди непреднамеренно нарушают это важное правило.

Начиная с 1990-х годов в системе здравоохранения возобладала концепция, согласно которой пожилые женщины должны принимать эстрогенные добавки, чтобы защититься от сердечно-сосудистых заболеваний, остеопороза и прочих недугов, связанных с менопаузой. К 2001 году эстрогенные добавки были предписаны примерно 15 миллионам женщин в надежде, что это снизит риск развития перечисленных заболеваний. На чем основывалась эта надежда? На проводившихся в то время исследованиях – с применением базовой методологии, описанной в предыдущей главе, – согласно которым прием эстрогенных добавок считался разумной медицинской стратегией. В частности, повторное исследование 122 000 женщин (так называемое Nurses’ Health Study) продемонстрировало наличие отрицательной зависимости между приемом эстрогенных добавок и сердечными приступами. Риск возникновения последних у женщин, принимающих эстроген, составлял примерно одну треть от соответствующего риска у женщин, которые его не принимали. Исследование проводилось, конечно, не парой подростков, использующих отцовский компьютер для просмотра порнофильмов и попутного решения уравнений регрессии, а Гарвардской медицинской школой и Гарвардской школой общественного здравоохранения.

Между тем, ученые и практикующие врачи выдвинули теорию, объясняющую, почему гормональные добавки могут быть полезны для здоровья женщин. В пожилом возрасте женские яичники вырабатывают меньше эстрогена, а поскольку он необходим женскому организму, то восполнение его дефицита в пожилом возрасте укрепляет здоровье женщины в долгосрочной перспективе. Отсюда и название метода: терапия путем замещения гормона. Некоторые исследователи рекомендовали эстрогенное стимулирование даже пожилым мужчинам.

А затем, после того как миллионам женщин была предписана заместительная гормонотерапия, эстроген подвергли более строгой форме научного исследования – клиническим испытаниям. Вместо того чтобы искать статистические взаимосвязи (которые могут выражать (или не выражать) реальную связь причины и следствия) в большой совокупности данных наподобие той, которая использовалась в ходе исследования Nurses’ Health Study, клинические испытания предусматривают проведение управляемого эксперимента. Одна выборка получает лечение (например, в виде терапии путем замещения гормона), а другая принимает плацебо. Клинические испытания показали, что у женщин, принимающих эстроген, более высокий уровень сердечно-сосудистых заболеваний, инсультов, образования тромбов, чаще диагностируется рак груди и наблюдаются прочие неблагоприятные для здоровья исходы. Эстрогенные добавки приносят определенную пользу, однако она полностью нивелируется дополнительными рисками. Начиная с 2002 года врачам было рекомендовано не назначать эстроген пожилым пациенткам. Остается только гадать, скольких женщин постигла преждевременная смерть, у скольких случился инсульт или развился рак груди из-за приема таблеток, которые якобы должны были укрепить их здоровье.

Вполне возможно, что их количество исчисляется десятками тысяч.

Регрессионный анализ – это своего рода водородная бомба в арсенале статистики. Каждый владелец персонального компьютера и большой совокупности данных может стать исследователем, не выходя из дома или не покидая стен офиса. В чем же причина проблем с регрессионным анализом? Таких причин очень много. Регрессионный анализ позволяет получить точные ответы на сложные вопросы, но они могут быть правильными или неправильными. В неумелых руках регрессионный анализ даст результаты, которые способны ввести в заблуждение или попросту оказаться неверными. И, как показывает пример с эстрогеном, даже в умелых руках этот мощный статистический инструмент может направить по ложному – и опасному! – пути. Задача настоящей главы – объяснить самые типичные «ошибки» регрессии. Слово «ошибки» я заключил в кавычки по той причине, что, как и в случае с другими видами статистического анализа, ловкие люди могут совершенно осознанно использовать их в неблаговидных целях.

Ниже перечислены семь самых типичных злоупотреблений этим замечательным инструментом.

Использование регресии для анализа нелинейной связи. Приходилось ли вам читать предостережение, которое обычно наносится на корпус фена для волос: «Не пользоваться во время мытья в ванне»? Читая эти слова, вы, наверное, думали: «Какой болван может до такого додуматься?» Ведь это электроприбор, им нельзя пользоваться в воде. Электроприборы для этого не предназначены. Если бы регрессионный анализ снабжался подобным предостережением, то оно должно было бы гласить: «Не пользоваться, когда между анализируемыми переменными существуют нелинейные зависимости». Запомните: коэффициент регрессии описывает степень наклона «линии наилучшего приближения» для рассматриваемых вами данных; непрямая линия будет характеризоваться разными степенями наклона в разных точках. Рассмотрим, например, следующую гипотетическую связь между числом уроков игры в гольф, которые я беру в течение месяца (объясняющая переменная), и моим средним результатом для восемнадцатилункового раунда за тот же месяц (зависимая переменная). Как нетрудно заметить из приведенной ниже диаграммы разброса данных, в этом случае отсутствует устойчивая линейная зависимость.

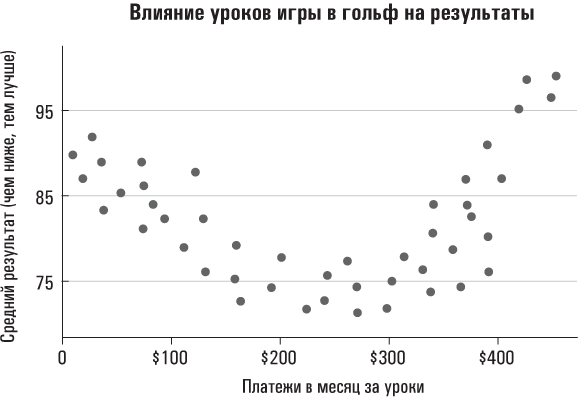
Итак, мы видим некую картину, которую невозможно описать с помощью одной прямой линии. Первые несколько уроков игры в гольф, похоже, привели к быстрому улучшению моих показателей (количество очков уменьшилось – в гольфе это считается положительным результатом). На этом отрезке времени наблюдается отрицательная зависимость между уроками и набранным мною количеством очков; наклон линии отрицательный. Чем больше уроков, тем меньше очков.

Но когда я начинаю тратить на уроки игры в гольф от 200 до 300 долларов в месяц, это, по-видимому, не оказывает на мои результаты вообще никакого влияния. На данном отрезке времени не наблюдается какой-либо четкой взаимосвязи между дополнительными уроками и моими результатами; наклон линии – нулевой.

Наконец наступает момент, когда уроки становятся контрпродуктивными. Если сумма, потраченная на уроки игры в гольф, достигает 300 долларов в месяц, дополнительные уроки ассоциируются с большим количеством набранных мною очков; на этом отрезке времени наблюдается положительный наклон линии. (Ниже в этой главе мы обсудим вероятность того, что плохие результаты игры в гольф могут стимулировать брать дополнительные уроки, а не наоборот.)

Самое важное здесь то, что с помощью единственного коэффициента регрессии мы не можем точно выразить зависимость между уроками и результатами. Наилучшей интерпретацией описанной выше картины будет то, что уроки игры в гольф характеризуются несколькими линейными связями с моими результатами. Вы можете видеть это, а пакет статистического программного обеспечения – нет. Если вы введете эти данные в уравнение регрессии, то компьютер выдаст вам единственный коэффициент. И он не будет точно отражать истинную взаимосвязь между интересующими нас переменными. Полученные результаты будут представлять собой статистический эквивалент использования фена для волос во время принятия ванны.

Регрессионный анализ предназначен для использования в случае линейной зависимости между переменными. В солидных учебниках по статистике указаны также другие базовые условия его применения. Как и при использовании любого другого инструмента, чем больше вы отклоняетесь от заранее оговоренных условий его применения, тем менее эффективным – и даже потенциально опасным – он становится.

Корреляция и причинно-следственные зависимости – не одно и то же. Регрессионный анализ может лишь продемонстрировать взаимосвязь между двумя переменными. Как я уже упоминал, с помощью только статистики невозможно доказать, что изменение одной переменной обусловило изменение другой переменной. Вообще говоря, неправильное уравнение регрессии может указать на существование внушительной и статистически значимой зависимости между двумя переменными, которые в действительности между собой никак не связаны. Допустим, мы планируем выявить потенциальные причины роста числа случаев аутизма в Соединенных Штатах за последние два десятилетия. Наша зависимая переменная – исход, который мы хотели бы объяснить, – могла бы служить показателем заболеваемости аутизмом, таким как количество диагностированных случаев на каждых 1000 детей определенного возраста. Если бы мы включили в качестве объясняющей переменной годовой доход на душу населения в Китае, то почти наверняка выявили бы положительную и статистически значимую зависимость между повышением доходов в Китае и ростом заболеваемости аутизмом в США за последние два десятилетия.

Чем это объясняется? Всего лишь тем, что оба показателя резко увеличились за указанный период. Между тем, я очень сомневаюсь, что наступление экономической рецессии в Китае приведет к снижению заболеваемости аутизмом в США. (Справедливости ради должен заметить, что если бы я наблюдал четкую связь между быстрым экономическим ростом в Китае и заболеваемостью аутизмом только в Китае, то я, возможно, приступил бы к поиску какого-либо фактора окружающей среды, связанного с экономическим ростом (например, загрязнение окружающей среды отходами промышленного производства), который мог бы объяснить подобную зависимость.)

Только что продемонстрированный мной род ложной зависимости между двумя переменными – лишь один пример более универсального явления, известного как фиктивные причинно-следственные связи. Существует несколько других вариантов, когда связь между A и B может быть неправильно интерпретирована.

Обратная причинно-следственная зависимость. Статистическая зависимость между A и B не доказывает, что A является причиной B. Вообще говоря, не исключено, что B – это причина A. Я указывал на такую вероятность ранее в примере с уроками игры в гольф. Допустим, что когда я построил сложную модель, чтобы объяснить свои результаты в гольфе, оказалось, что переменная, обозначающая количество уроков игры в гольф, демонстрирует четкую взаимосвязь с ухудшением моих показателей. Чем больше уроков я беру, тем хуже результаты! Одним из объяснений может быть то, что мне попался очень плохой тренер. Более правдоподобное объяснение: я обычно беру дополнительные уроки, когда начинаю плохо играть, то есть плохие результаты являются причиной увеличения количества уроков, а не наоборот. (Существует ряд простых методологических исправлений проблем такого рода. Например, я мог бы включить количество уроков игры в гольф в одном месяце в качестве объясняющей переменной для моих показателей в следующем месяце.)

Как указывалось выше в этой главе, причинно-следственные связи могут действовать в обоих направлениях. Допустим, согласно проводимому вами исследованию, штаты, которые тратят больше денег на школьное образование, демонстрируют более высокие темпы экономического роста, чем штаты, вкладывающие в школьное образование меньше денег. Наличие положительной и значимой зависимости между этими двумя переменными ничего нам не говорит о направлении этой зависимости. Инвестиции в программу школьного образования могут вызывать экономический рост. С другой стороны, штаты, демонстрирующие более высокие темпы экономического роста, могут себе позволить больше инвестировать в школьное образование; стало быть, сильная экономика может быть причиной увеличения расходов на образование. Другой вариант: дополнительные траты на школьное образование могут стимулировать экономический рост, что позволяет вкладывать больше средств в образование, то есть причинно-следственные связи могут носить двусторонний характер.

Следовательно, мы не должны использовать объясняющие переменные, зависящие от исхода, который мы пытаемся объяснить, – в противном случае результаты могут оказаться безнадежно запутанными. Например, было бы неуместно использовать коэффициент безработицы в уравнении регрессии, объясняющем рост ВВП, поскольку совершенно очевидно, что уровень безработицы зависит от темпов роста ВВП. Или, иначе говоря, результат регрессионного анализа, заключающийся в том, что снижение безработицы обусловит рост ВВП, представляется совершенно бессмысленным, потому что именно рост ВВП обычно приводит к снижению безработицы.

У нас должны быть все основания полагать, что наши объясняющие переменные влияют на зависимую переменную, а не наоборот.

Систематическая ошибка, вызванная пропущенной переменной. Увидев в газете броский заголовок: «Игроки в гольф чаще болеют сердечно-сосудистыми заболеваниями, раком и артритом!», не относитесь к нему серьезно. Я не был бы удивлен, если бы это было так. Я также подозреваю, что гольф полезен для здоровья, поскольку обеспечивает не только возможность социализации, но и умеренную физическую нагрузку. Как совместить оба утверждения? Очень просто! Любое исследование, измеряющее влияние игры в гольф на состояние здоровья человека, должно надлежащим образом контролировать возраст. Вообще говоря, гольфом в большей степени увлекаются люди старших возрастов – особенно пенсионеры. Любой анализ, не принимающий во внимание возраст как объясняющую переменную, упускает из виду тот факт, что гольфисты в среднем – более пожилые люди, чем те, кто в него не играет. Не гольф убивает людей, а старость. Так уж случается, что гольф предпочитают именно пожилые люди. Я полагаю, что при использовании возраста в регрессионном анализе в качестве управляющей переменной мы получим другой результат: для людей одного и того же возраста игра в гольф может стать профилактикой серьезных заболеваний. Это весьма существенная разница.

В данном примере возраст – важная «пропущенная переменная». Когда мы не учитываем его в уравнении регрессии, объясняющем развитие сердечно-сосудистых заболеваний или какие-то другие исходы, неблагоприятные для здоровья человека, переменная «увлечение игрой в гольф» исполняет две объясняющие роли, а не одну. Она говорит о влиянии игры в гольф на состояние сердечно-сосудистой системы и о влиянии старости на состояние сердечно-сосудистой системы. На языке статистики это будет звучать примерно так: переменная «увлечение игрой в гольф» подхватывает (учитывает) влияние возраста. Проблема заключается в том, что эти два влияния объединяются. В лучшем случае наши результаты оказываются весьма запутанными. В худшем мы приходим к ошибочному выводу, что гольф плохо сказывается на здоровье человека, хотя на самом деле вероятнее обратное утверждение.

Результаты регрессии будут вводить нас в заблуждение и страдать неточностью в случае отсутствия в уравнении регрессии какой-либо важной объясняющей переменной, особенно если другие переменные в этом уравнении «подхватывают» данный эффект. Допустим, мы пытаемся объяснить качество школ. Нам очень важно понять, что именно делает школы хорошими. Нашей зависимой переменной – численным показателем качества – будут, вероятнее всего, результаты экзаменов. Мы почти наверняка станем рассматривать расходы школы как одну объясняющую переменную в надежде найти численное выражение связи между расходами и результатами экзаменов. Можно ли утверждать, что школы, у которых больше расходы, добиваются лучших результатов? Если бы расходы школы были единственной объясняющей переменной, я не сомневаюсь, что нам удалось бы выявить четкую и статистически значимую зависимость между ними и итогами экзаменов. Однако такой вывод, а также вытекающее из него следствие, будто улучшить качество школ можно путем повышения расходов, глубоко ошибочны.

Здесь есть немало потенциально значимых пропущенных переменных, однако важнейшей из них будет уровень образования родителей. Высокообразованные семьи, как правило, проживают в престижных районах. А расположенные в этих районах школы обычно расходуют немалые средства. К тому же дети в таких семьях демонстрируют хорошие результаты на экзаменах (тогда как баллы детей из малоимущих семей гораздо хуже). Если у нас нет какого-либо показателя социально-экономического статуса учащихся, который можно было бы использовать в качестве управляющей переменной, то результаты нашей регрессии наверняка укажут на четкую положительную зависимость между расходами школы и итогами экзаменов, тогда как в действительности эти результаты могут быть функцией социально-экономического положения учащихся школы, а не суммы денег, израсходованных ею.

Я помню, как один из преподавателей нашего колледжа утверждал, что результаты школьных экзаменов высоко коррелированны с количеством автомобилей, которыми владеет семья. Этим он как бы намекал на несправедливость школьных тестов и невозможность использовать их итоги в качестве основного критерия при поступлении в колледж. Разумеется, система школьных экзаменов не лишена недостатков, но корреляция между их результатами и количеством автомобилей в семье вовсе не то, что тревожит меня больше всего. Меня мало волнует, что богачи могут устроить своих детей в колледж, купив еще три автомобиля. Количество автомобилей в семейном гараже является показателем дохода соответствующей семьи, уровня образования ее членов и прочих признаков их социально-экономического статуса. То обстоятельство, что дети из состоятельных семей сдают экзамены успешнее их менее зажиточных сверстников, не новость. (Как отмечалось ранее, средний балл сдачи стандартизированного теста по чтению у учащихся из семей, совокупный доход которых превышает 200 000 долларов, на 134 балла выше, чем средний результат сдачи такого же теста детьми из семей, совокупный доход которых не превышает 20 000 долларов.) Гораздо больше меня интересует вероятность улучшить результаты сдачи стандартизированного теста путем «натаскивания» ученика. Насколько ученик может их улучшить, воспользовавшись услугами частных репетиторов? Очевидно, у состоятельных семей гораздо больше возможностей нанять для своих детей хороших репетиторов. Любое улучшение результатов сдачи экзаменов учащимися, занимающимися с репетиторами (если, конечно, это не чистая случайность), говорит в пользу детей из состоятельных семей по сравнению с их менее зажиточными сверстниками, даже если способности тех и других совершенно одинаковы, – ведь ученики из малообеспеченных семей тоже могли бы улучшить свои результаты, если бы воспользовались услугами частных репетиторов (однако им это не по карману).

Сильно коррелированные объясняющие переменные (мультиколлинеарность). Если уравнение регрессии включает две объясняющие переменные (или даже больше), сильно коррелированные между собой, то анализ вполне может не выявить истинной зависимости между каждой из этих переменных и исходом, который мы пытаемся объяснить. Приведу соответствующий пример. Допустим, мы хотим измерить влияние противозаконного использования наркотиков на результаты сдачи экзаменов. В частности, мы располагаем данными о том, употребляли ли когда-либо участники нашего исследования кокаин и «баловались» ли когда-либо героином. (Будем исходить из того, что в нашем распоряжении есть и много других управляющих переменных.) Каково влияние употребления кокаина на результаты сдачи экзаменов (при условии неизменности всех остальных факторов, включая употребление героина)? А каково влияние употребления героина на итоги экзаменов (при условии неизменности всех остальных факторов, включая употребление кокаина)?

Вполне возможно, что коэффициенты по употреблению героина и кокаина не смогут ответить на интересующие нас вопросы. Методологическая проблема в данном случае заключается в том, что те, кто «баловался» героином, наверняка употребляли и кокаин. Если поместить в уравнение обе переменные, то число тех, кто употреблял один из этих наркотиков, но не употреблял другой, окажется очень незначительным. Это оставит нам довольно мизерное расхождение в данных, на основании которого мы могли бы вычислить их независимые влияния. Вспомните мысленный эксперимент, который мы провели в предыдущей главе, чтобы объяснить регрессионный анализ. Мы распределили выборку данных по разным комнатам, в которых каждое наблюдение идентично за исключением одной переменной, что позволяло затем вычленить влияние этой переменной, параллельно контролируя другие факторы, потенциально способные сказываться на интересующем нас исходе. В нашей выборке может быть 692 человека, которые употребляли и кокаин, и героин. Но у нас может быть и всего три человека, которые употребляли только кокаин, и два человека, употреблявших только героин. Любой вывод относительно независимого влияния лишь одного или другого наркотика будет основываться на этих крошечных выборках.

Вряд ли нам удастся получить достоверные коэффициенты регрессии по какой-либо из этих двух переменных (кокаин или героин); мы можем также проигнорировать более сильную и важную зависимость между результатами экзаменов и употреблением какого-то одного из этих наркотиков. Когда две объясняющие переменные сильно коррелированны между собой, исследователи обычно используют в уравнении регрессии какую-то одну из них; как вариант, они могут создать некую составную переменную, например «употреблял кокаин или героин». Если же исследователи хотят контролировать в целом социально-экономическое положение учащегося, они могут включить переменные «образование матери» и «образование отца», поскольку это обеспечивает важное указание на уровень образования соответствующей семьи в целом. Однако если цель регрессионного анализа – вычленить влияние либо образования отца, либо образования матери, то включение в уравнение обеих переменных скорее запутает вопрос, чем внесет в него ясность. Корреляция между уровнями образования мужа и жены столь высока, что мы не можем полагаться на то, что регрессионный анализ даст нам коэффициенты, которые позволят надлежащим образом вычленить влияние образования кого-либо из родителей (это так же трудно, как обособить влияние употребления кокаина от влияния употребления героина).

Экстраполяция за границы имеющихся данных. Регрессионный анализ, как и все формы статистического вывода, помогает нам лучше понять окружающий мир. Мы пытаемся выявить закономерности, которые будут общими и для более крупной совокупности. Однако наши результаты будут справедливы лишь для совокупности, подобной выборке, в отношении которой выполнялся анализ. В предыдущей главе я создал уравнение регрессии, позволяющее предсказывать вес, основываясь на ряде независимых переменных. Значение R² в моей окончательной модели равнялось 0,29; это означает, что оно дает возможность объяснить разброс веса для крупной выборки людей, если все они оказались взрослыми.

Итак, что же произойдет, если мы воспользуемся нашим уравнением регрессии для предсказания вероятного веса новорожденного младенца? Давайте проверим. При рождении рост моей дочери составлял 21 дюйм. Допустим, ее возраст в момент рождения равнялся нулю; у нее, конечно же, не было образования и она не занималась спортом. Она относилась к белой расе и была женского пола. Уравнение регрессии, основанное на данных America’s Changing Lives, предсказывает, что ее вес при рождении должен иметь отрицательную величину: ‒19,6 фунта. (В действительности она весила 8,5 фунта.)

Авторы одного из исследований, выполнявшихся по заказу британского правительства (мы упоминали о них в предыдущей главе), сделали совершенно четкий вывод: «Неспособность работника влиять на свою рабочую среду ассоциируется с повышенным риском развития заболеваний сердечно-сосудистой системы среди государственных служащих» (курсив мой).

Интеллектуальный анализ (слишком много переменных). Если игнорирование важных переменных представляет собой потенциальную проблему, то, может быть, ее возможным решением будет максимальное наращивание количества объясняющих переменных в уравнении регрессии? Отнюдь! Ваши результаты могут быть поставлены под угрозу, если вы включите в уравнение регрессии чересчур большое число переменных, особенно если речь идет о дополнительных объясняющих переменных без какого-либо теоретического обоснования такого решения. Например, не следует разрабатывать стратегию исследования, построенную на следующей предпосылке: поскольку нам неизвестно, что вызывает аутизм, нужно включить в уравнение регрессии как можно больше потенциальных объясняющих переменных, чтобы увидеть, что именно может оказаться статистически значимым; затем, возможно, мы сумеем получить кое-какие ответы. Если вы включите в уравнение регрессии достаточно большое число лишних переменных, то одна из них, по чистой случайности, обязательно достигнет порога статистической значимости. Еще одна опасность заключается в том, что лишние переменные порой не так-то легко распознать именно как лишние. Опытные исследователи могут всегда обосновать теоретически, постфактум, почему та или иная необычная переменная, которая в действительности совершенно бессмысленна, оказывается статистически значимой.

Чтобы доказать это, я нередко проделываю то же упражнение с подбрасыванием монетки, которое приводил при обсуждении вероятностей. В аудитории примерно из сорока студентов я предлагаю каждому подбросить монетку. Все, у кого выпадает решка, выводятся из игры; остальные продолжают подбрасывание. Во втором раунде те, у кого выпадает решка, снова выводятся из игры. Я продолжаю раунды до тех пор, пока у кого-то из студентов пять или шесть раз подряд не выпадет орел. Наверняка вам придут на память глупые вопросы, которые обычно задают в таких случаях: «В чем ваш секрет? Вы достаете этих орлов из рукава? Можете ли вы научить нас подбрасывать монетку так, чтобы каждый раз выпадал орел? Может быть, все дело в фирменной футболке Гарвардского университета, в которой вы пришли сегодня на лекцию?»

Разумеется, череда следующих друг за другом выпаданий орлов – чистая случайность: студенты, присутствовавшие в аудитории, были свидетелями происходящего. Однако полученный результат мог по-разному интерпретироваться в научном контексте. Вероятность пятикратного (подряд) выпадания орлов равняется 1/32, или 0,03. Это существенно ниже порога 0,05, который мы обычно используем, чтобы отвергнуть основную гипотезу. Наша нулевая гипотеза в данном случае заключается в том, что этот студент не обладает особым талантом подбрасывать монетку. Тем не менее удачная череда выпаданий орлов (которая обязательно произойдет по крайней мере у одного студента, если этот эксперимент будет проводиться с достаточно большим количеством участников) позволяет нам отклонить нулевую гипотезу и принять альтернативную гипотезу, утверждающую, что данный студент обладает особым талантом подбрасывать монетку так, чтобы каждый раз выпадал орел. После того как он достиг этого впечатляющего результата, мы можем подвергнуть его более детальному изучению в надежде выявить причины столь блестящих достижений: методика подбрасывания монетки, особая физическая подготовка, умение полностью сконцентрироваться на монетке, пока она вращается в воздухе, и т. п. Все это совершеннейшая чепуха!

Подобное явление способно расстроить даже безупречно организованное исследование. Считается, что нулевую гипотезу следует отвергнуть, когда мы наблюдаем нечто, что должно было бы произойти по чистой случайности не чаще, чем в 1 случае из 20, если бы наша основная гипотеза была верна. Разумеется, если мы проведем 20 исследований или включим в одно уравнение регрессии 20 лишних переменных, то в среднем получим один ложный статистически значимый результат. Журнал The New York Times блестяще выразил это противоречие, процитировав Ричарда Пето, медицинского статистика и эпидемиолога: «Эпидемиология так восхитительна и позволяет получить столь важные представления о жизни и смерти человека! Удручает лишь невероятное количество никому не нужных, бестолковых публикаций».

Даже к результатам клинических испытаний, которые обычно представляют собой статистические эксперименты и, следовательно, являются «золотым стандартом» медицинских исследований, следует относиться с изрядной долей скептицизма. В 2011 году газета The Wall Street Journal разместила на первой странице материал, который охарактеризовала как один из «грязных маленьких секретов» медицинских исследований: «Большинство результатов, в том числе и публикуемых в солидных научных периодических изданиях, рецензируемых коллегами авторов статей, невозможно воспроизвести повторно». (Речь идет о публикациях, предварительно проверяемых с точки зрения их методологической надежности другими экспертами в той же области; лишь после такой проверки материал отправляется в печать. Такие публикации принято считать заслуживающими особого доверия с научной точки зрения.) Одна из причин этого «грязного маленького секрета» – систематическая ошибка позитивной публикации, описанная в главе 7. Если исследователи и медицинские журналы склонны обращать внимание на позитивные результаты и игнорировать негативные, то они вполне могут опубликовать итоги исследования, свидетельствующие об эффективности некоего лекарства, и проигнорировать девятнадцать других исследований, доказывающих его бесполезность. Некоторые клинические испытания могут также основываться на небольших выборках (что бывает обусловлено объективными факторами, например редко встречающейся болезнью), что повышает вероятность того, что случайное отклонение в данных привлечет к себе больше внимания, чем оно того заслуживает. Самое главное – у исследователей может быть предубеждение (осознаваемое или нет), вызванное или непоколебимой уверенностью в чем-либо, или пониманием того, что позитивный результат будет способствовать их научной карьере. (Никто еще не разбогател и не стал знаменитым, доказав, что то или иное лекарство не излечивает от рака.)

В силу всех перечисленных причин количество экспертных исследований, результаты которых оказались ошибочными, очень велико. Джон Иоаннидис, греческий врач-эпидемиолог, проанализировал итоги сорока девяти исследований, опубликованных в трех солидных медицинских журналах. Каждое из них цитировалось в медицинской литературе не менее тысячи раз. Тем не менее примерно треть результатов впоследствии была опровергнута дальнейшими экспериментами. (Например, некоторые из исследований, проанализированных Иоаннидисом, доказывали эффективность упоминавшейся выше терапии путем замещения эстрогена.) По оценкам д-ра Иоаннидиса, выводы примерно половины опубликованных научных статей в конце концов оказываются ошибочными. Его исследование было опубликовано в Journal of the American Medical Association, одном из журналов, в которых печатались проанализированные им статьи. Из этого следует забавный парадокс: если исследование д-ра Иоаннидиса верно, то вполне вероятно, что его исследование ошибочно.

Регрессионный анализ по-прежнему остается потрясающим статистическим инструментом. (Похоже, мои эпитеты в его адрес заставляют относиться к нему как к «волшебному эликсиру», о котором я упоминал в предыдущей главе. Разумеется, мои слова не лишены некоторого преувеличения.) Он позволяет выявлять важные закономерности в крупных совокупностях данных, которые зачастую оказываются ключом к серьезным исследованиям в медицине и социальных науках. Статистика предоставляет нам объективные стандарты для оценивания этих закономерностей. Регрессионный анализ, при надлежащем использовании, – значимая составляющая научного метода. Считайте эту главу предупреждением, к которому обязательно нужно прислушаться.

Все конкретные предостережения, о которых шла речь в этой главе, можно свести к двум ключевым положениям. Во-первых, создание эффективного уравнения регрессии – то есть определение, какие переменные нужно проанализировать и что должно быть источником соответствующих данных, – важнее самих статистических вычислений. Этот процесс называется оцениванием адекватности уравнения или выбором правильного уравнения регрессии. Лучшие исследователи – те, кто может путем логических умозаключений решить, какие переменные включить в уравнение регрессии, какие проигнорировать и как следует интерпретировать конечные результаты.

Во-вторых, как и большинство других статистических выводов, регрессионный анализ выстраивает лишь некую версию, основанную на косвенных доказательствах. Зависимость между двумя переменными подобна отпечаткам пальцев, оставленным на месте преступления. Она указывает на преступника, но одних лишь отпечатков недостаточно, чтобы осудить человека. (К тому же они могут ему не принадлежать.) Любой регрессионный анализ нуждается в теоретическом обосновании. Почему в уравнение регрессии включены именно эти объясняющие переменные? Какие явления из других областей могут объяснить наблюдаемые результаты? Например, почему мы считаем, что красные туфли у экзаменуемых способствуют значительному улучшению результатов сдачи школьных экзаменов или что употребление попкорна помогает предотвратить рак простаты? Соответствующие результаты должны быть повторно воспроизводимыми или по крайней мере не должны противоречить итогам других исследований.

Даже волшебный эликсир может не оказать должного эффекта, если не пользоваться им так, как предписано.