11. Регрессионный анализ
Волшебный эликсир

Может ли стресс на работе стать причиной вашей смерти? Да, вполне. Существуют убедительные доказательства того, что суровые условия на работе могут привести к преждевременной смерти, особенно в результате развития сердечно-сосудистых заболеваний. Однако это не тот вид стресса, о котором вы, наверное, подумали. Главы компаний, которым буквально каждый день приходится принимать чрезвычайно сложные и ответственные решения, определяющие дальнейшую судьбу их бизнеса, рискуют значительно меньше, чем их секретарши, бесконечно отвечающие на телефонные звонки, параллельно выполняя множество других задач, предусмотренных должностной инструкцией. Как такое может быть? Оказывается, самый опасный вид стресса на работе обусловлен невозможностью человека в достаточной степени контролировать способы и условия выполнения поставленных задач. Ряд исследований, проводившихся (по заказу правительства) в отношении тысяч британских мелких чиновников, показал, что от них практически не зависит, чем именно им предстоит заниматься и как именно это выполнять, что и является причиной их высокой смертности по сравнению с чиновниками более высоких рангов, ответственных за принятие важных решений. Согласно результатам исследования, человека убивает не стресс, связанный с повышенной ответственностью, а стресс, вызванный необходимостью делать работу, не имея возможности решать, как и когда.

Но не пугайтесь, эта глава не о стрессе на работе, сердечно-сосудистых заболеваниях или государственных служащих Британии. Нас прежде всего интересует, как ученые приходят к подобным выводам. Очевидно, что это не результат рандомизированного эксперимента. Мы не можем произвольно поручать людям некую работу, заставляя их долгие годы ею заниматься, а затем выяснять, кто из них раньше умер. (Случайным образом поручая людям выполнение тех или иных задач, мы рискуем нанести огромный вред государственной службе Британии, не говоря уже об этической стороне дела.) Вместо этого исследователи собирали о тысячах государственных служащих Британии подробные повторные данные, анализ которых позволяет выявить определенные связи, например между невозможностью человека в достаточной степени контролировать способы и условия выполнения своей работы и развитием сердечно-сосудистых заболеваний.

Но такой связи мало для того, чтобы сделать вывод о вреде тех или иных видов работ для здоровья человека. Если мы просто замечаем, что мелкие государственные служащие в иерархии британской государственной службы страдают сердечно-сосудистыми заболеваниями чаще других, то полученные нами результаты будут искажаться действием ряда других факторов. Например, можно было бы ожидать, что уровень образования мелких чиновников окажется ниже, чем у чиновников более высоких рангов. Может также выясниться, что среди мелких государственных служащих больше курящих (не исключено, что это объясняется их неудовлетворенностью работой). Вполне вероятно, что у этих людей было трудное детство, и это сузило перспективы их будущего карьерного роста. Или их невысокий уровень доходов не позволяет им уделять должное внимание своему здоровью. И так далее. Дело в том, что любое сравнительное исследование – изменение состояния здоровья у большой группы британских работников или какой-то другой крупной группы населения – не позволяет нам сделать далекоидущие выводы. Возможно, что другие источники изменения полученных нами данных внесут искажения в интересующую нас связь. Можем ли мы быть уверены в том, что именно невозможность человека в достаточной степени контролировать содержание, способы и условия выполнения своей работы является подлинной причиной развития у него сердечно-сосудистых заболеваний? Или истинная причина – в сочетании действия ряда факторов, которые оказались общими для данной категории людей?

Статистический инструмент под названием регрессионный анализ помогает решить данную проблему. А если конкретнее, то регрессионный анализ позволяет нам измерить величину зависимости между какой-то переменной и интересующим нас исходом, зафиксировав действие всех прочих факторов. Другими словами, мы можем вычленить влияние одной переменной (например, занятие определенным родом деятельности), сохраняя на постоянном уровне действие других переменных. Регрессионный анализ использовался при проведении упоминавшегося нами исследования, которое проводилось по заказу британского правительства и имело своей целью оценить, как невозможность человека в достаточной степени контролировать содержание, способы и условия выполнения своей работы сказывается на состоянии здоровья людей, схожих во всех остальных отношениях, например курильщиков. (Рядовые работники действительно курят больше своих начальников; это объясняет относительно малую величину разброса в сердечно-сосудистых заболеваниях во всей иерархии британской государственной службы.)

Большинство исследований, о которых вам приходилось читать в прессе, основываются на регрессионном анализе. Когда ученые приходят к выводу, что у детей, посещавших детсад, чаще возникают проблемы с успеваемостью в начальной школе, чем у детей, которые воспитывались дома, это вовсе не означает, что они случайным образом сформировали выборку из нескольких тысяч детей, одну половину которых отправили в детсады, а другую оставили на попечении родителей. Это также не означает, что исследователи просто сравнили успеваемость в начальной школе детей, посещавших детсад, и детей, находившихся дома, не отдавая себе отчета в том, что эти две группы детей фундаментально разнятся между собой по ряду других показателей. В разных семьях принимаются разные решения относительно воспитания детей именно потому, что эти семьи – разные. В одних семьях детей воспитывают оба родителя, в других – только один. Есть семьи, где работают оба родителя, а есть – где только один. Какие-то семьи более состоятельны и образованны, какие-то менее. Все эти факторы так или иначе сказываются на принятии решений относительно воспитания детей и не могут не влиять на их успеваемость во время учебы в начальной школе. В случае надлежащего выполнения регрессионный анализ помогает оценить влияние воспитания, исключив из рассмотрения другие факторы воздействия на детей: семейный доход, структуру семьи, образование родителей и т. п.

В приведенном выше предложении есть два ключевых словосочетания. Первое: «в случае надлежащего выполнения». Сегодня при наличии соответствующих данных и доступа к персональному компьютеру даже шестилетний ребенок может воспользоваться какой-либо статистической программой для получения результатов регрессионного анализа, поскольку это не потребует практически никаких умственных усилий. Проблема не в выполнении регрессионного анализа как такового, главная трудность – определить, какие именно переменные следует рассматривать в этом анализе и как это лучше всего сделать. Регрессионный анализ подобен многим современным универсальным электромеханическим инструментам: им относительно легко пользоваться, но трудно это делать эффективно, не говоря уже о том, что при ненадлежащем использовании, то есть неумелом обращении, он оказывается потенциально опасен.

Второе важное словосочетание: «помогает оценить». Наше исследование воспитания детей не дает нам «правильного» ответа относительно зависимости между способом воспитания ребенка (в детсаду или дома) и его успеваемостью в начальной школе. Вместо этого оно оценивает величину этой связи у конкретной группы детей на определенном отрезке времени. Можем ли мы сделать выводы, применимые к более широкой совокупности? Да, но при этом нам придется иметь дело с такими же ограничениями и условиями, с какими мы сталкиваемся, делая любой другой статистический вывод. Во-первых, используемая нами выборка должна быть репрезентативной, то есть представлять всю интересующую нас совокупность. Исследование 2000 детей в Швеции не позволит нам прийти к сколь-нибудь значимым выводам относительно оптимальных методов дошкольного образования детей в сельскохозяйственных районах Мексики. И во-вторых, не следует забывать о существовании разброса между выборками. Если мы выполняем ряд исследований, касающихся детей и их воспитания, то их результаты будут несколько отличаться между собой, даже если используемые при этом методологии будут одинаковы и совершенно надежны.

Регрессионный анализ подобен проведению опросов общественного мнения. Обнадеживает то, что при применении крупной репрезентативной выборки и правильной методологии наблюдаемая взаимосвязь между данными выборки не должна существенно отличаться от истинной взаимосвязи для совокупности в целом. Если у 10 000 человек, занимающихся спортом не менее трех раз в неделю, уровень заболеваемости сердечно-сосудистой системы значительно ниже, чем у 10 000 человек, не занимающихся спортом (но не отличающихся от первых 10 000 человек во всех остальных отношениях), то весьма высока вероятность того, что мы будем наблюдать аналогичную связь между регулярными занятиями спортом и уровнем заболеваемости сердечно-сосудистой системы для более широкой совокупности. Именно поэтому мы выполняем исследования такого рода. (Задача ученых вовсе не в том, чтобы по завершении исследования упрекнуть тех, кто не занимается спортом и имеет проблемы с сердцем, что в свое время им не следовало игнорировать эти занятия.)

Плохо, однако, то, что мы не можем с полной уверенностью утверждать, что занятия спортом предотвращают возникновение сердечно-сосудистых заболеваний. Вместо этого мы отвергаем нулевую гипотезу о том, что занятия спортом никак не связаны с болезнями сердца. Отвергнуть ее нам позволяет достижение определенного статистического порога, выбранного еще до начала выполнения исследования. Если конкретнее, то авторы данного исследования должны были бы указать, что в случае, если занятия спортом никак не связаны с сердечно-сосудистыми заболеваниями, вероятность наблюдения столь заметной разницы в уровне заболеваемости сердечно-сосудистой системы между теми, кто регулярно занимается спортом, и теми, кто им не занимается, в этой крупной выборке должна быть менее 0,05 или ниже какого-то другого порога статистической значимости.

Давайте остановимся на мгновение и помашем нашим первым гигантским желтым флагом. Допустим, что в этом конкретном исследовании сравнивалась большая группа людей, регулярно играющих в сквош, с людьми из такой же по величине группы, которые вообще не занимаются спортом. Игра в сквош обеспечивает неплохую нагрузку на сердечно-сосудистую систему. Однако нам также известно, что игроки в сквош – достаточно состоятельные люди, чтобы быть членами клубов, располагающих хорошими сквош-кортами. Богатые люди могут себе позволить уделять должное внимание здоровью, что также способствует снижению заболеваемости их сердечно-сосудистой системы. Если выполненный нами анализ страдает небрежностями, то хорошее состояние здоровья можно объяснить игрой в сквош, хотя на самом деле оно объясняется высокими доходами, которые дают человеку возможность играть в сквош (в таком случае даже увлечение игрой в поло можно при желании связать с хорошим состоянием здоровья, если, конечно, закрыть глаза на то, что во время игры в поло большая часть физической работы выполняется лошадью).

Ничто не мешает нам также предположить, что причинно-следственные связи имеют противоположную направленность. Может быть, здоровое сердце является «причиной» того, что человек занимается спортом? Почему бы и нет! Те, кто не блещет здоровьем, – особенно люди с врожденными заболеваниями сердца, – не могут полноценно заниматься спортом, что вполне понятно. Вряд ли они в состоянии регулярно играть в сквош. Опять-таки, если выполненный нами анализ сделан небрежно или чрезмерно упрощен, утверждение о том, что занятия спортом способствуют улучшению здоровья, может лишь отражать то обстоятельство, что тем, кто им не блещет, бывает очень нелегко заниматься спортом. В этом случае игра в сквош никоим образом не улучшает состояние здоровья – а лишь отделяет здоровых от больных.

Существует так много потенциальных «регрессионных ловушек», что я решил посвятить их рассмотрению всю следующую главу. Пока же будем считать, что на нашем пути ни одна из них не встретится. Регрессионный анализ обладает замечательным свойством вычленять в каждом отдельном случае статистическую связь, которая представляет для нас интерес, например связь между невозможностью человека в достаточной степени контролировать содержание, способы и условия выполнения своей работы и развитием сердечно-сосудистых заболеваний, учитывая при этом другие факторы, которые могут внести в нее искажения.

Как действует данный механизм? Если нам известно, что мелкие государственные служащие Британии курят чаще, чем их начальники, то как нам определить, в какой мере плохое состояние их сердечно-сосудистой системы обусловлено спецификой работы, а в какой – этой пагубной привычкой? Оба фактора кажутся неразрывно связанными между собой.

Регрессионный анализ (выполненный надлежащим образом!) позволяет разделить эти факторы. Чтобы объяснить процесс на интуитивном уровне, мне придется начать с базовой идеи, лежащей в основе всех форм регрессионного анализа, от простейших статистических связей до сложных моделей, разработанных лауреатами Нобелевской премии. По своей сути регрессионный анализ стремится найти «наилучшее приближение» линейной зависимости между двумя переменными. Простой пример – зависимость между ростом и весом людей. Те, кто выше ростом, как правило, весят больше, хотя эта закономерность соблюдается не всегда. Если бы мы построили диаграмму разброса для роста и веса группы студентов-выпускников, то получили бы нечто наподобие того, что уже видели в главе 4.

Если бы вас попросили описать получившуюся картину, вы бы наверняка сказали что-то вроде: «Вес, по-видимому, увеличивается пропорционально росту». Такую догадку вряд ли можно назвать озарением. Регрессионный анализ позволяет нам пойти дальше и «провести линию», которая точнее всего отражает линейную зависимость между этими двумя переменными.

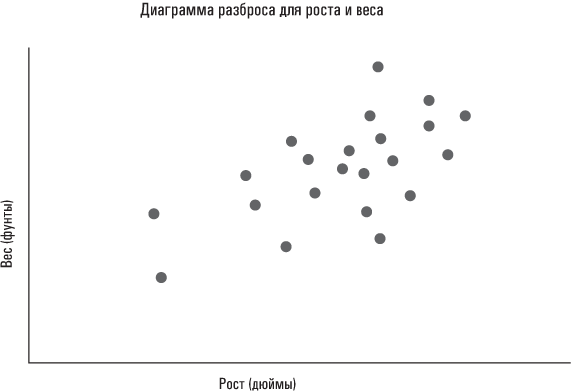
Можно провести множество линий, которые будут отражать соотношение между ростом и весом. Но как знать, какая из них это делает точнее всего? К тому же посредством какого критерия мы определяем эту линию? Регрессионный анализ обычно использует методологию под названием стандартный метод наименьших квадратов, МНК. Если читателя интересуют его технические подробности и он хочет узнать, почему МНК обеспечивает «наилучшее приближение», ему придется обратиться к более солидным учебникам по статистике. Ключевыми словами в названии МНК являются «наименьшие квадраты»: МНК определяет линию, минимизирующую сумму квадратов разностей. Это не настолько сложно, как может показаться на первый взгляд. Каждое наблюдение в нашей совокупности данных «рост/вес» характеризуется разностью, которая представляет собой его расстояние по вертикали от линии регрессии; это не относится к наблюдениям, расположенным непосредственно на линии: для них разность равняется нулю. (На представленной ниже диаграмме разброса разность отмечена для некоего гипотетического лица A.) На интуитивном уровне должно быть понятно, что чем больше сумма разностей в целом, тем худшее приближение обеспечивает данная линия. Единственное, что может быть непонятно в МНК на интуитивном уровне, это то, что в соответствующей формуле суммируются квадраты каждой разности (тем самым увеличивается весовой коэффициент, назначаемый наблюдениям, которые расположены особенно далеко от линии регрессии, то есть «отщепенцам»).

Обычный метод наименьших квадратов позволяет определить линию, которая минимизирует сумму квадратов разностей, как показано ниже.

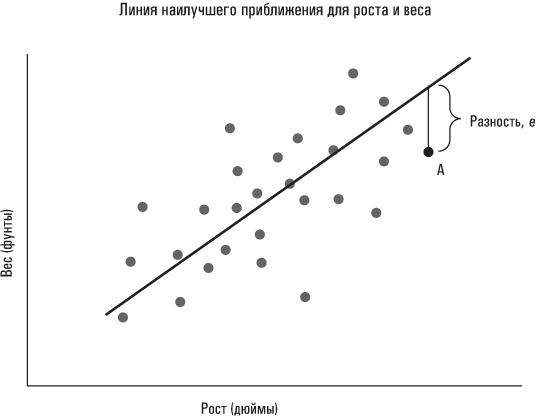
Если технические подробности вызывают у вас головную боль, можете не обращать на них внимания. Важно запомнить главное: стандартный метод наименьших квадратов позволяет получить наилучшее описание линейной зависимости между двумя переменными. В результате мы получаем не только линию как таковую, но и – как вы, наверное, помните из курса геометрии в средней школе – уравнение, описывающее ее. Оно известно как уравнение регрессии и имеет следующий вид: y = a + bx, где y – вес в фунтах, a – отрезок, отсекаемый этой линией на оси Y (то есть значение y, когда x = 0), b – коэффициент наклона линии, а x – рост в дюймах. Коэффициент наклона b найденной нами линии описывает «наилучшую» линейную зависимость между ростом и весом для соответствующей выборки, как определяется стандартным методом наименьших квадратов.

Линия регрессии, конечно, не описывает идеальным образом каждое наблюдение в соответствующей совокупности данных. Но как бы то ни было, это лучшее из возможных описаний зависимости между весом и ростом человека. Это также означает, что каждое наблюдение можно объяснить как Вес = a + b(Рост) + e, где e – «разность», представляющая собой отклонение веса для каждого человека, которое не объясняется его ростом. Наконец, это означает, что наше оптимальное предположение относительно веса какого-либо человека в рассматриваемой совокупности даных будет иметь такой вид: a + b(Рост). Несмотря на то что большинство наблюдений не лежат непосредственно на линии регрессии, ожидаемая величина разности все же равняется нулю, поскольку вероятность того, что вес любого человека в выборке окажется больше, чем прогнозирует уравнение регрессии, равна вероятности того, что его вес окажется меньше, чем прогнозирует уравнение регрессии.

Впрочем, довольно теоретического жаргона! Давайте посмотрим на реальные данные роста и веса из исследования Americans’ Changing Lives. Правда, вначале мне придется прояснить кое-какую базовую терминологию. Переменная, которая подлежит объяснению, – в нашем случае это вес – называется зависимой переменной, так как она зависит от других факторов. Переменные, используемые для объяснения зависимой переменной, называются объясняющими переменными, поскольку они объясняют интересующий нас результат. (Чтобы еще больше запутать мозги, объясняющие переменные иногда называют независимыми или управляющими переменными.) Начнем с использования роста, чтобы объяснить вес участников исследования Americans’ Changing Lives, а впоследствии добавим другие потенциальные объясняющие факторы. В исследовании Americans’ Changing Lives участвуют 3537 взрослых. В нашем случае это количество наблюдений, или n. (Иногда в научных статьях это обозначается так: n = 3537.) Когда мы выполняем простую регрессию по отношению к данным Americans’ Changing Lives, где вес – зависимая переменная, а рост – единственная объясняющая переменная, то получаем следующие результаты:

Вес = −135 + 4,5 × Рост в дюймах

a = −135. Это не что иное, как отрезок, отсекаемый линией регрессии на оси Y; никакого специального объяснения у этой величины нет. (Если интерпретировать ее буквально, то получается, что человек с нулевым ростом весил бы –135 фунтов [отрицательная величина]; очевидно, что это нонсенс с любой точки зрения.) Эту величину также называют константой, поскольку она является отправной точкой для вычисления веса всех наблюдений в исследовании.

b = 4,5. Наша оценка для b (4,5) называется коэффициентом регрессии или, на статистическом жаргоне, «коэффициентом по росту», поскольку такой коэффициент служит наилучшей оценкой зависимости между ростом и весом участников исследования Americans’ Changing Lives. У коэффициента регрессии имеется удобная интерпретация: увеличение на одну единицу независимой переменной (рост) ассоциируется с увеличением на 4,5 единицы зависимой переменной (вес). Для нашей выборки данных это означает, что увеличение роста на один дюйм сопряжено с увеличением веса на 4,5 фунта. Таким образом, если бы мы не располагали никакой другой информацией, то нашим оптимальным предположением относительно веса участника исследования Americans’ Changing Lives, рост которого составляет 5 футов и 10 дюймов (то есть 70 дюймов), было бы –135 + 4,5 × 70 = 180 фунтов.

Это наша победа, поскольку нам удалось получить численное выражение наилучшего приближения линейной зависимости между ростом и весом участников исследования Americans’ Changing Lives. Те же самые базовые инструменты можно использовать для исследования более сложных зависимостей и получения ответов на более социально значимые вопросы. При любом коэффициенте регрессии вас, по сути, будут интересовать три вещи: знак, величина и значимость.

Знак. Знак (положительный или отрицательный) при коэффициенте для независимой переменной указывает направление его связи с зависимой переменной (исход, который мы пытаемся объяснить). В рассматриваемом нами случае коэффициент по росту является положительным. Более высокие люди, как правило, имеют больший вес. Некоторые зависимости действуют в противоположном направлении. Скажем, можно ожидать, что связь между занятиями спортом и весом будет отрицательной. Если бы в исследовании Americans’ Changing Lives фигурировали, например, данные о «количестве миль, пробегаемых участником за один месяц», то я бы нисколько не сомневался, что коэффициент по «количеству пробегаемых миль» будет отрицательным: чем большее количество миль вы ежемесячно пробегаете, тем меньше ваш вес.

Величина. Насколько велика наблюдаемая нами зависимость между независимой и зависимой переменными? Можно ли считать ее величину существенной для нас? В рассматриваемом нами случае увеличение роста человека на дюйм ассоциируется с прибавкой веса на 4,5 фунта; в процентном выражении это значительная доля массы тела типичного человека. В объяснении того, почему одни люди весят больше, чем другие, рост, несомненно, является важным фактором. В других исследованиях мы можем обнаружить объясняющую переменную, которая оказывает статистически значимое влияние на интересующий нас исход (это означает, что наблюдаемый эффект вряд ли объясняется чистой случайностью), но оно порой бывает настолько малым, что может считаться несущественным, или незначимым. Например, допустим, что мы исследуем определяющие факторы дохода. Объясняющими переменными здесь могут быть образование, стаж работы и т. п. При использовании достаточно крупного набора данных ученые также могут прийти к выводу, что люди с более белыми зубами зарабатывают на 86 долларов в год больше, чем остальные работники, ceteris paribus. (Ceteris paribus по-латыни означает «при прочих равных условиях».) Положительный и статистически значимый коэффициент по переменной «белые зубы» предполагает, что те, кого мы сравниваем, в остальном (по уровню образования, рабочему стажу и т. п.) не различаются между собой. (Ниже я объясню, каким образом мы можем выполнить это условие.) Наш статистический анализ продемонстрировал, что более белые зубы ассоциируются с 86-долларовой прибавкой к годовому доходу и что этот эффект вряд ли объясняется чистой случайностью. Это означает, что 1) мы с достаточно высокой степенью уверенности отвергли основную (нулевую) гипотезу, гласящую, что наличие у человека белых зубов никак не связано с уровнем его годового дохода; и 2) если мы проанализируем другие выборки данных, то наверняка обнаружим аналогичную связь между хорошо выглядящими зубами и повышенным уровнем дохода.

Что же из этого следует? Мы выявили статистически значимый результат, хотя для нас он практически бесполезен. Начнем с того, что прибавка в 86 долларов к годовому доходу вряд ли существенно изменит уровень жизни человека. С экономической точки зрения она вряд ли оправдывает регулярное выполнение процедур по отбеливанию зубов, поскольку такие процедуры наверняка обойдутся гораздо дороже, поэтому нам не имеет смысла рекомендовать подобные инвестиции молодым работникам. И, несколько забегая вперед, я озаботился бы также рядом серьезных методологических проблем. Например, идеальный вид зубов может ассоциироваться с другими чертами характера человека, обусловливающими более высокий уровень его доходов: то есть дело не в зубах как таковых, а в том, что люди с высоким уровнем доходов, как правило, заботятся об их состоянии. Пока же для нас важно обратить внимание на степень (величину) наблюдаемой нами связи между объясняющей переменной и интересующим нас исходом.

Значимость. Является ли наблюдаемый нами результат заблуждением, обусловленным нерепрезентативной выборкой данных, или он отражает реально существующую связь, которая, скорее всего, будет присуща всей соответствующей совокупности? Это тот же самый фундаментальный вопрос, на который мы пытаемся ответить на протяжении нескольких последних глав. Можно ли ожидать в контексте роста и веса, что мы будем наблюдать аналогичную положительную ассоциацию в других выборках, которые являются репрезентативными по отношению к данной совокупности? Чтобы ответить на этот вопрос, используем уже знакомые вам базовые инструменты статистического вывода. Наш коэффициент регрессии основывается на наблюдаемой зависимости между ростом и весом для определенной выборки данных. Если бы мы тестировали более крупную выборку, то почти наверняка выявили бы несколько иную зависимость между ростом и весом и, следовательно, другой коэффициент регрессии. Зависимость между ростом и весом, наблюдаемая в данных, полученных британским правительством (напоминаю, что они касаются государственных служащих Британии), безусловно, будет отличаться от зависимости между ростом и весом для участников исследования Americans’ Changing Lives. Однако из центральной предельной теоремы следует, что среднее значение для большой, надлежащим образом сформированной выборки, как правило, не будет существенно отклоняться от среднего значения для генеральной совокупности. Аналогично мы можем предположить, что наблюдаемая зависимость между переменными, такими как рост и вес, тоже не будет значительно разниться от выборки к выборке, если, конечно, эти выборки будут достаточно крупными и надлежащим образом сформированными из одной и той же совокупности.

Вы должны понимать это на интуитивном уровне. Весьма маловероятно (хотя в принципе возможно), что, обнаружив зависимость между каждым дополнительным дюймом роста и дополнительными 4,5 фунта веса участников исследования Americans’ Changing Lives, мы в то же время не выявили бы никакой зависимости между ростом и весом в какой-то другой репрезентативной выборке, состоящей из 3000 взрослых американцев.

Это должно дать вам первый намек на то, как мы будем проверять, являются ли результаты нашей регрессии статистически значимыми. Для коэффициента регрессии, как и для опросов общественного мнения и других форм статистического вывода, мы можем вычислить стандартную ошибку, которая представляет собой показатель вероятного разброса, наблюдаемый нами в значениях этого коэффициента в случае, если бы мы выполнили регрессионный анализ по нескольким выборкам, сформированным из одной и той же совокупности. Если бы мы измерили рост и вес в какой-то другой выборке, состоящей из 3000 взрослых американцев, то последующий анализ мог бы показать, что каждый дополнительный дюйм роста ассоциируется с дополнительными 4,3 фунта веса. Если бы мы проделали те же самые действия в отношении еще одной выборки из 3000 взрослых американцев, то могли бы обнаружить, что каждый дополнительный дюйм роста связан с дополнительными 5,2 фунта веса. И здесь на помощь снова приходит нормальное распределение. При использовании больших выборок данных можно предположить, что полученные нами разные коэффициенты регрессии будут распределены по нормальному закону вблизи «истинной» зависимости между ростом и весом в совокупности взрослых американцев. В таком предположении мы можем вычислить стандартную ошибку для коэффициента регрессии, что позволит составить представление о том, насколько большой разброс коэффициентов регрессии следует ожидать от выборки к выборке. Я не буду здесь вдаваться в подробное объяснение формулы для вычисления стандартной ошибки, поскольку для этого пришлось бы прибегнуть к множеству математических выкладок и к тому же все базовые статистические пакеты программного обеспечения вычислят ее за вас.

Однако должен предупредить, что при использовании небольшой выборки данных – например группы из 20 взрослых американцев вместо группы из более чем 3000 участников исследования Americans’ Changing Lives – нормальное распределение на помощь нам уже не придет. В частности, если мы будем то и дело выполнять регрессионный анализ в отношении разных малых выборок, то уже не сможем исходить из того, что полученные нами разные коэффициенты регрессии будут распределены по нормальному закону вблизи «истинной» зависимости между ростом и весом в совокупности взрослых американцев. Вместо этого они будут распределены вблизи «истинной» зависимости между ростом и весом в совокупности взрослых американцев по закону, известному как t-распределение, или распределение Стьюдента. (Вообще говоря, t-распределение характеризуется большей степенью разброса, чем нормальное распределение, и, следовательно, имеет «более толстые хвосты».) Все прочее остается неизменным; любые базовые статистические пакеты программного обеспечения без проблем справятся с дополнительной сложностью, связанной с использованием t-распределений. Поэтому более подробное объяснение t-распределения приведено в к этой главе.

Пока же будем исходить из того, что имеем дело с большими выборками (и с нормальным распределением). Самое главное сейчас – понять, почему для нас так важна стандартная ошибка. Как и в случае с опросами общественного мнения и другими формами статистического вывода, мы ожидаем, что более половины наблюдаемых коэффициентов регрессии будут отстоять от истинного параметра совокупности на расстояние, не превышающее одной стандартной ошибки. Примерно 95 % коэффициентов регрессии будут отстоять от истинного параметра совокупности на расстояние, не превышающее двух стандартных ошибок. И так далее. Учитывая сказанное, можно считать, что мы почти у цели, так как теперь можем выполнить небольшую проверку гипотез. (А вы и в самом деле полагали, что с проверкой гипотез покончено?) Поскольку у нас уже есть коэффициент и стандартная ошибка, мы можем проверить основную гипотезу, которая заключается в том, что между объясняющей и зависимой переменной на самом деле никакой зависимости нет (а это, в свою очередь, означает, что истинная зависимость между ними в данной совокупности равна нулю).

В нашем простом примере с ростом и весом мы можем проверить, какова вероятность обнаружить, что в выборке Americans’ Changing Lives каждый дополнительный дюйм роста ассоциируется с 4,5 дополнительных фунта веса, если на самом деле во всей совокупности зависимость между ростом и весом отсутствует. Я вычислил соответствующую регрессию, воспользовавшись одним из распространенных статистических пакетов; стандартная ошибка по коэффициенту роста составила 0,13. Это означает, что в случае многократного выполнения такого анализа (скажем, с сотней разных выборок) можно было бы ожидать, что наш наблюдаемый коэффициент регрессии будет отстоять от истинного параметра совокупности на расстояние, не превышающее двух стандартных ошибок, примерно в 95 случаях из 100.

Следовательно, это позволяет нам выразить полученные результаты двумя разными, но взаимосвязанными между собой способами. Первый – это построить 95 %-ный доверительный интервал. Мы можем утверждать, что в 95 случаях из 100 доверительный интервал (который составляет 4,5 ± 0,26) будет включать истинный параметр совокупности. Это диапазон от 4,24 до 4,76. Любой из статистических пакетов также вычислит этот интервал. Второй – отвергнуть основную гипотезу об отсутствии зависимости между ростом и весом для совокупности в целом на 95 %-ном доверительном уровне, видя, что наш 95 %-ный доверительный интервал для истинной зависимости между ростом и весом не включает нуль. Этот результат можно также выразить как статистически значимый на уровне 0,05: существует лишь 5 %-ная вероятность того, что мы ошибочно отвергли основную гипотезу.

На самом деле наши результаты еще более убедительны, чем кажется на первый взгляд. Стандартная ошибка (0,13) очень мала по сравнению с величиной коэффициента (4,5). Практика показывает, что этот коэффициент можно считать статистически значимым, когда его величина по меньшей мере в два раза превышает величину стандартной ошибки. Любой из базовых статистических пакетов также вычисляет p-значение, которое в данном случае равняется 0,000; это означает, что если в действительности зависимости между ростом и весом в совокупности в целом нет, то вероятность получить столь необычный результат, какой нам удалось наблюдать, по сути, равна нулю. Не забывайте, что мы вовсе не доказали, что более рослые люди весят больше во всей совокупности, а лишь показали, что если бы это было не так, то наши результаты для выборки Americans’ Changing Lives были бы крайне маловероятными.

Базовый регрессионный анализ дает еще одну статистику, заслуживающую внимания, R², которая предсталяет собой показатель суммарной величины разброса, объясняемого уравнением регрессии. Нам известно, что в выборке Americans’ Changing Lives наблюдается широкий разброс веса. Многие члены выборки весят больше среднего веса для данной группы в целом; многие – меньше. Величина R² говорит нам, какая доля этого разброса вокруг среднего значения ассоциируется лишь с различиями в росте. В нашем случае эта доля составляет 0,25, или 25 %. Более значимым может быть то обстоятельство, что 75 % этого разброса в весе для нашей выборки остаются необъясненными. Есть очевидные факторы, помимо роста, которые могут нам помочь их объяснить. Ситуация становится интереснее.

В начале этой главы я объявил регрессионный анализ чудодейственным эликсиром для социальных исследований. До сих пор я использовал некий базовый статистический пакет и впечатляющие данные, чтобы продемонстрировать тот факт, что рослые люди, как правило, весят больше коротышек. Краткая прогулка по какому-нибудь супермаркету наверняка убедила бы вас в том же. Теперь пора оценить реальные возможности регрессионного анализа. Иными словами, пора пересаживаться с детского трехколесного велосипеда на велосипед для взрослых!

Как я уже говорил, регрессионный анализ позволяет распутывать сложные взаимосвязи, в которых многие факторы оказывают влияние на интересующий нас исход, например доход, или результаты экзамена, или развитие сердечно-сосудистых заболеваний. Когда мы включаем в уравнение регрессии несколько переменных, анализ дает оценку линейной зависимости между каждой объясняющей и зависимой переменной, оставляя при этом неизменными другие зависимые переменные (то есть «контролируя» их). Давайте на какое-то время сосредоточимся на весе. Мы выявили зависимость между ростом и весом, а также знаем о существовании других факторов (возраст, пол, режим питания, занятия спортом и т. п.), которые могут помочь объяснить вес. Посредством регрессионного анализа (часто называемого множественным регрессионным анализом, если в нем задействовано несколько объясняющих переменных, или многофакторным регрессионным анализом) можно вычислить некий коэффициент регрессии для каждой объясняющей переменной, задействованной в уравнении регрессии. Скажем, какова зависимость между возрастом и весом среди людей одного и того же пола и роста. Когда нам приходится иметь дело с несколькими объясняющими переменными, соответствующие данные уже невозможно отобразить на двумерной диаграмме. (Попытайтесь представить себе диаграмму, которая отображает вес, пол, рост и возраст каждого участника исследования Americans’ Changing Lives.) Тем не менее базовая методология остается той же, что и в примере с ростом и весом. При добавлении объясняющих переменных статистический пакет будет вычислять коэффициенты регрессии, которые минимизируют общую сумму квадратов разностей для соответствующего уравнения регрессии.

Пока ограничимся данными исследования Americans’ Changing Lives, а затем я вернусь и предложу интуитивно понятное объяснение того, как действует этот механизм. Мы можем начать с добавления в уравнение регрессии еще одной переменной, которая объясняет вес участников Americans’ Changing Lives, – «возраст». Когда мы вычислим уравнение регрессии, включающее рост и возраст в качестве объясняющих переменных, то получим вот что:

Вес = −145 + 4,6 × (Рост в дюймах) + 0,1 × (Возраст в годах)

Коэффициент возраста равняется 0,1. Это можно интерпретировать так: каждый дополнительный год к возрасту человека ассоциируется с 0,1 дополнительных фунта к весу человека при неизменном росте. Для любой группы людей одного и того же роста те, кто на десять лет старше, весят в среднем на один фунт больше. Как видим, влияние возраста на вес человека не так уж велико, но это соответствует тому, что мы обычно наблюдаем в реальной жизни. Данный коэффициент является значимым на уровне 0,05.

Возможно, вы заметили, что коэффициент для роста несколько увеличился. После того как мы включили в нашу регрессию возраст, у нас появилось уточненное понимание зависимости между ростом и весом. Среди людей одного возраста в выборке (иными словами, при фиксированном возрасте) каждый дополнительный дюйм роста ассоциируется с дополнительными 4,6 фунта веса.

Теперь давайте добавим еще одну переменную – пол. Тут есть один нюанс: пол может принимать лишь два значения (мужской и женский). Как вставить эти «М» и «Ж» в регрессию? Благодаря использованию так называемой двоичной, или фиктивной переменной. Вводим в нашей совокупности данных 1 для участников-женщин и 0 – для участников-мужчин. (Дорогие мужчины, пожалуйста, не обижайтесь!) При этом коэффициент пола можно интерпретировать как влияние на вес того обстоятельства, что данный участник является женщиной – при прочих равных условиях (ceteris paribus). Этот коэффициент составляет –4,8, что не должно вызывать у вас удивления. Это можно истолковать так: когда речь идет об участниках одного и того же роста и возраста, женщины обычно весят на 4,8 фунта меньше мужчин. Теперь вам уже должны быть в какой-то мере ясны богатые возможности множественного регрессионного анализа. Нам известно, что женщины обычно ниже мужчин, и наш коэффициент учитывает это обстоятельство, поскольку мы уже контролируем рост (мы его «зафиксировали»). В данном случае мы рассматриваем влияние пола – точнее говоря, женского пола. Новая регрессия принимает следующий вид:

Наша «наилучшая» оценка веса пятидесятитрехлетней женщины, рост которой равен 5 футов и 5 дюймов, такова: −118 + 4,3 × 65 + 0,12 × 53 − 4,8 = 163 фунта.

Наша «наилучшая» оценка веса тридцатипятилетнего мужчины, рост которого составляет 6 футов и 3 дюйма, такова: −118 + 4,3 × 75 + 0,12 × 35 = 209 фунтов. Мы опускаем последний член (−4,8) при вычислении результата регрессии, поскольку рассматриваемый нами человек не является женщиной.

Теперь давайте приступим к проверке более интересных и менее предсказуемых вещей. Что можно сказать по поводу образования? Как оно может влиять на вес? Я бы выдвинул гипотезу, что более образованные люди в большей степени заботятся о своем здоровье и, следовательно, весят меньше. Кроме того, мы еще не проверяли влияние занятий спортом; я полагаю, что при прочих равных условиях члены нашей выборки, регулярно занимающиеся спортом, весят меньше.

А что можно сказать по поводу бедности? Не сказываются ли низкие доходы части американцев на их весе? В исследовании Americans’ Changing Lives есть вопрос о том, получает ли его участник продовольственные талоны. (Продовольственные талоны в Соединенных Штатах выдаются только малоимущим гражданам.) Наконец, меня интересует расовая принадлежность человека. Нам известно, что люди разных рас в США имеют разный жизненный опыт именно вследствие своей расовой принадлежности. С той или иной расой в Соединенных Штатах ассоциируются определенные культурные факторы и места компактного проживания. Все эти факторы могут оказывать влияние на вес человека. Многие города Америки характеризуются высокой степенью расовой сегрегации: афроамериканцы чаще других американских граждан проживают в так называемых продовольственных пустынях, то есть территориях с ограниченным доступом к продовольственным магазинам, где продаются свежие фрукты, овощи и другая свежая продукция.

Регрессионный анализ можно использовать для обособления независимого влияния каждого из потенциальных объясняющих факторов, описанных выше. Например, мы можем вычленить связь между расовой принадлежностью и весом человека, сохраняя постоянными другие социально-экономические факторы, такие как уровень образования и бедность. Существует ли статистически достоверная связь между весом человека и его принадлежностью к негроидной расе, если речь идет о людях, окончивших среднюю школу и имеющих право на получение продовольственных талонов?

В данном случае уравнение регрессии окажется таким длинным, что было бы весьма проблематично привести его здесь полностью. Научные статьи обычно включают огромные таблицы, обобщающие результаты разных уравнений регрессии. В приложении к этой главе вы найдете таблицу с полными результатами этого уравнения регрессии. Между тем, я могу подсказать, что произойдет, если мы добавим в уравнение такие факторы, как уровень образования человека, его склонность к занятиям спортом, показатель бедности (исходя из которого определяется его право на получение продовольственных талонов) и расовая принадлежность.

Все наши исходные переменные (рост, возраст и пол) по-прежнему остаются значимыми. При добавлении объясняющих переменных несколько изменяются коэффициенты. Новые переменные являются статистически значимыми на уровне 0,05. Значение R² для этой регрессии повысилось с 0,25 до 0,29. (Вспомните: нулевая величина R² означает, что уравнение регрессии прогнозирует вес любого человека в данной выборке ничуть не лучше, чем среднее значение; если же R² равно 1, то наше уравнение регрессии идеально прогнозирует вес каждого человека в данной выборке.) Существенная доля разброса величин веса среди членов данной выборки остается необъясненной.

Как я и предполагал, зависимость между образованием и весом человека оказалась отрицательной. Среди участников исследования Americans’ Changing Lives каждый дополнительный год образования ассоциируется с −1,3 фунта веса.

Неудивительно, что физические упражнения также отрицательно связаны с весом человека. Исследование Americans’ Changing Lives включает индекс, который оценивает каждого участника исследования с точки зрения уровня его физической активности. Те, кто находится в нижнем квинтиле склонности к регулярным занятиям спортом, весят в среднем на 4,5 фунта больше, чем другие взрослые в этой выборке, ceteris paribus. И примерно на 9 фунтов больше, чем взрослые в верхнем квинтиле склонности к регулярным занятиям спортом.

Вес тех, кто получает продовольственные талоны (что служит показателем бедности в этой регрессии), больше, чем у других взрослых. Получатели продовольственных талонов весят в среднем на 5,6 фунта больше, чем другие участники исследования Americans’ Changing Lives, ceteris paribus.

Переменная расовой принадлежности представляет особый интерес. Даже если мы зафиксируем все остальные вышеперечисленные переменные, расовая принадлежность сыграет довольно важную роль в объяснении веса. Неиспаноязычные взрослые негроидной расы в выборке Americans’ Changing Lives весят в среднем примерно на 10 фунтов больше, чем другие взрослые в выборке. Десять фунтов – весьма существенная прибавка в весе как в абсолютном выражении, так и по сравнению с влиянием других объясняющих переменных в нашем уравнении регрессии. И это вовсе не какой-то случайный «выверт» данных. p-значение по фиктивной переменной для неиспаноязычных взрослых негроидной расы равняется 0,000, а 95 %-ный доверительный интервал охватывает величины веса от 7,7 фунта до 16,1 фунта.

Что же происходит? Честно говоря, не имею понятия. Могу лишь повторить замечание, сделанное мною выше в одной из сносок: я лишь экспериментирую с данными, чтобы проиллюстрировать принцип действия регрессионного анализа. Представленные здесь аналитические материалы призваны подтвердить результаты научного исследования значения дворового хоккея для НХЛ. (Шутка.) Если бы это был реальный исследовательский проект, то для подтверждения правильности его выводов понадобились бы недели и даже месяцы аналитической работы. Могу лишь сказать, что я продемонстрировал вам, почему множественный регрессионный анализ – лучший из имеющихся в нашем распоряжении инструмент для поиска существенных закономерностей в больших и сложных совокупностях данных. Мы начали со смехотворно банального упражнения: поиска численного выражения связи между ростом и весом, а затем перешли к рассмотрению вопросов, имеющих реальное социальное значение.

В этом ключе я могу предложить вам реальное исследование, в котором регрессионный анализ использовался для решения социально значимой проблемы – дискриминации по половому признаку на рабочем месте. Такую дискриминацию, как правило, трудно наблюдать непосредственно. Никто из работодателей не скажет вам напрямую, что тому или иному работнику платят меньше только по причине его расовой или половой принадлежности или что кого-то не приняли на работу по каким-либо дискриминационным соображениям (в результате чего этот человек, наверное, нашел другую работу, но с более низкой заработной платой). Однако на практике мы наблюдаем различия в зарплате по расовому или половому признаку, которые могут быть следствием дискриминации: белые зарабатывают больше, чем черные; мужчины – больше, чем женщины, и т. д. Методологическая проблема заключается в том, что эти различия могут также оказаться результатом других различий между работниками, которые не имеют ничего общего с дискриминацией (например, женщины зачастую предпочитают работать неполный рабочий день). В какой мере имеющаяся разница в оплате труда обусловлена факторами, связанными с производительностью на работе, а в какой – с дискриминацией работников (если таковая вообще присутствует)? Никто не станет утверждать, что этот вопрос относится к разряду тривиальных.

Регрессионный анализ может помочь нам на него ответить. Однако в этом случае наша методология будет несколько более «окольной», чем в примере с анализом, объясняющим вес. Поскольку дискриминация не поддается непосредственному измерению, нам придется исследовать другие факторы (например образование, производственный стаж, род занятий и т. п.), которые традиционно объясняют уровень заработной платы. Мы можем действовать методом исключения: если после фиксации этих факторов все же останется существенная разница в зарплате, то дискриминация на работе, по-видимому, имеет место. Чем больше необъясненная доля разницы в заработной плате, тем сильнее подозрения в наличии дискриминации на рабочем месте. Рассмотрим статью трех экономистов, исследующих траектории заработной платы в выборке, состоящей примерно из 2500 мужчин и женщин – выпускников Booth School of Business Чикагского университета (все они обладатели степени MBA). Сразу после выпуска средний начальный уровень заработной платы у мужчин и женщин приблизительно одинаков: 130 000 долларов у мужчин и 115 000 долларов у женщин. Однако через десять лет образуется огромный разрыв: женщины в среднем зарабатывают на целых 45 % меньше, чем их бывшие однокурсники-мужчины: 243 000 долларов против 442 000 долларов. В более широкой выборке, включающей свыше 18 000 выпускников (обладающих степенью MBA), которые приступили к работе в период с 1990 по 2006 год, у женщин на 29 % ниже заработки, чем у мужчин. Что же происходит с женщинами, после того как они выходят на рынок труда?

Согласно авторам данного исследования (Марианна Бертран из Booth School of Business, Клаудиа Голдин и Лоуренс Кац из Гарвардского университета), дискриминация не является вероятным объяснением большей доли разрыва в зарплатах. Причем разрыв по половому признаку исчезает, когда авторы добавляют в анализ дополнительные объясняющие переменные. Например, при прохождении программы MBA мужчины посещают дополнительные курсы финансов и на выпускных экзаменах получают в среднем более высокие оценки. Когда эти данные используются в уравнении регрессии в качестве управляющих переменных, необъясненная доля разрыва в уровнях зарплаты мужчин и женщин снижается до 19 %. Когда же в это уравнение включаются переменные, позволяющие учитывать рабочий стаж после окончания университета, необъясненная доля разрыва в уровнях зарплаты мужчин и женщин снижается до 9 %. А когда в уравнение добавляются объясняющие переменные для других характеристик (например, тип работодателя и количество реально отработанных часов), необъясненная доля разрыва в уровнях зарплаты мужчин и женщин снижается до менее 4 %.

Что касается работников, стаж которых превышает десять лет, то авторы исследования могут в конечном счете объяснить все, кроме 1 %-ного разрыва в уровнях зарплаты мужчин и женщин, факторами, не имеющими никакого отношения к дискриминации на работе. Авторы пришли к следующему выводу: «Мы выявили три непосредственные причины существования большого увеличивающегося разрыва в уровнях зарплаты мужчин и женщин: разница в уровнях знаний, полученных в высшем учебном заведении; разница, обусловленная большими перерывами в стаже у женщин; разница в количестве реально отрабатываемых часов в неделю. Эти три детерминанта могут объяснить львиную долю разрыва в уровнях зарплаты мужчин и женщин по окончании ими вуза и после начала трудовой деятельности».

Я надеюсь, что убедил вас в полезности множественного регрессионного анализа, особенно в возможности делать выводы по результатам исследований путем обособления влияния какой-то одной объясняющей переменной и фиксации («контроля») других факторов, способных вносить искажения в выводы. Я еще не предложил вам интуитивно понятного объяснения того, как этот статистический «волшебный эликсир» работает. Когда мы используем регрессионный анализ для оценивания зависимости между образованием и весом человека, ceteris paribus, как применяемый нами статистический пакет контролирует такие факторы, как рост, пол, возраст и доход, когда нам доподлинно известно, что участники исследования Americans’ Changing Lives вовсе не идентичны в других отношениях?

Чтобы уяснить, каким образом можно изолировать влияние на вес какой-либо отдельно взятой переменной, например образования, давайте представим следующую ситуацию. Допустим, что все участники исследования Americans’ Changing Lives собрались в каком-то одном месте, например во Фрамингеме. Теперь предположим, что мы отделили мужчин от женщин, а затем распределили их по росту. В одном помещении собрали всех мужчин, рост которых равняется шести футам; в соседнем – рост которых равняется шести футам и одному дюйму и т. д. для представителей обоих полов. Если в нашем исследовании участвует достаточно много людей, мы можем разбить их на группы по уровню дохода и распределить по разным комнатам. В каждой комнате будут находиться люди, идентичные во всех отношениях, за исключением образования и веса, которые и являются двумя интересующими нас переменными. В результате описанного распределения обязательно окажется комната, где соберутся сорокапятилетние мужчины ростом 5 футов и 5 дюймов, годовой доход которых составляет от 30 000 до 40 000 долларов. В соседней комнате будут находиться сорокапятилетние женщины ростом 5 футов и 5 дюймов и годовым доходом от 30 000 до 40 000 долларов. И так далее.

В каждой комнате все же будет наблюдаться некоторый разброс величин веса: вес людей одного пола и роста, имеющих примерно одинаковый доход, будет разным, хотя, наверное, в этом случае эта разница будет гораздо меньшей, чем в выборке в целом. Сейчас наша цель – увидеть, какую долю остающегося разброса величин веса в каждой комнате можно объяснить уровнем образования. Иными словами, какова «наилучшая» линейная связь между образованием и весом в каждой комнате?

Конечная проблема, однако, заключается в том, что мы не хотели бы использовать разные коэффициенты для каждой комнаты. Весь смысл этого упражнения – рассчитать единственный коэффициент, который бы наилучшим образом отражал связь между образованием и весом для рассматриваемой нами выборки в целом – при неизменности других факторов. Мы хотели бы определить единый коэффициент для образования, который можно было бы использовать в каждой комнате, чтобы минимизировать сумму квадратов разностей для совокупности всех комнат. Какой коэффициент для образования минимизирует квадрат необъясненного веса для каждого человека по всем комнатам? Этот коэффициент становится нашим коэффициентом регрессии, поскольку является наилучшим объяснением линейной зависимости между образованием и весом для данной выборки при неизменности таких факторов, как пол, рост и доход.

Данный пример позволяет понять, почему так полезны большие совокупности данных. Они дают нам возможность контролировать многие факторы, располагая при этом большим количеством наблюдений в каждой «комнате». Очевидно, компьютер может выполнить соответствующие вычисления буквально за доли секунды, не распределяя тысячи людей по разным комнатам.

Завершу главу тем же, с чего начал, – зависимостью между стрессом на работе и развитием сердечно-сосудистых заболеваний. Цель исследований, выполняемых по заказу британского правительства в отношении государственных служащих, заключалась в том, чтобы определить связь между невозможностью человека в достаточной степени контролировать содержание, способы и условия выполнения своей работы и развитием сердечно-сосудистых заболеваний за определенный период времени. В ходе одного из первых исследований, проводившегося на протяжении семи с половиной лет, использовалась выборка из 17 530 государственных служащих. Авторы исследования пришли к следующему заключению: «Служащие (мужчины) низшего ранга, как правило, ниже ростом, полнее, имеют проблемы с артериальным давлением, больше курят и меньше занимаются спортом, чем чиновники более высоких рангов. Даже после внесения поправки, учитывающей влияние на уровень смертности всех этих факторов плюс содержание холестерина в крови, отрицательная закономерность между рангом госслужащего и уровнем смертности от сердечно-сосудистых заболеваний оставалась достаточно сильной». Упоминаемая «поправка» вносится посредством регрессионного анализа. Результаты исследования демонстрируют, что при фиксации остальных факторов здоровья (включая рост, который является надежным показателем здоровья и качества питания в раннем детстве) работа на «низких» должностях может в буквальном смысле вас убить.

Скептицизм – вполне разумная первая реакция. В начале главы я написал, что невозможность человека в достаточной степени влиять на содержание, способы и условия выполнения своей работы отрицательно сказывается на его здоровье. Это может быть (или не быть) синонимом пребывания работника на нижних ступенях административной иерархии. Дальнейшее исследование, в ходе которого использовалась вторая выборка из 10 308 британских государственных служащих, было призвано более глубоко уяснить эту разницу. Работников еще раз разделили на административные ранги – высокий, промежуточный и низкий, – но на сей раз предложили заполнить анкету из пятнадцати пунктов, чтобы оценить уровень «диапазона принятия решений или контроля» работника. Анкета содержала вопросы типа: «Можете ли вы выбирать, как именно будете выполнять порученную вам работу?»; кроме того, предлагались разные варианты ответа (от «никогда» до «часто») на утверждения наподобие: «Я могу самостоятельно решать, когда устроить себе перерыв». Исследователи пришли к выводу, что за время проведения эксперимента у работников с «низким уровнем контроля» риск развития сердечно-сосудистых заболеваний был значительно выше, чем у работников с «высоким уровнем контроля». Вместе с тем ученые обнаружили, что риск развития сердечно-сосудистых заболеваний у служащих с жесткими требованиями к выполняемой работе ничуть не выше, чем у работников с низким уровнем социальной поддержки на работе. Похоже, что невозможность человека в достаточной степени влиять на содержание, способы и условия выполнения поставленных задач убивает его в буквальном смысле этого слова.

Упомянутое нами исследование британских служащих обладает двумя характеристиками, типичными для таких солидных экспериментов. Во-первых, его результаты подтверждены аналогичными исследованиями в других странах. В медицинской литературе представление о «низком контроле» (то есть недостаточной возможности человека влиять на содержание, способы и условия выполнения своей работы) привело к появлению термина «переутомление на работе», который характеризует должности с «высокой психологической нагрузкой» и «недостаточностью полномочий для принятия решений». В период с 1981 по 1993 год были опубликованы результаты тридцати шести исследований по этому вопросу; в большинстве из них найдена значительная положительная взаимосвязь между переутомлением на работе и развитием сердечно-сосудистых заболеваний.

Во-вторых, исследователи выявили дополнительные биологические свидетельства, объясняющие механизм, посредством которого этот особый вид стресса на работе приводит к ухудшению здоровья работника. Условия работы, предусматривающие строгие требования, но не позволяющие человеку влиять на процесс выполнения поставленных задач, могут вызывать физиологические реакции (например выделение гормонов, связанных со стрессом), повышающие риск развития сердечно-сосудистых заболеваний в долгосрочной перспективе. Раскрыть этот механизм помогают даже опыты над животными: у обезьян и павианов, занимающих низкий статус (и имеющих немало общего с мелкими государственными служащими), есть физиологические отличия от их высокостатусных сородичей, причем эти отличия обусловливают их большую склонность к сердечно-сосудистым заболеваниям.

При прочих равных условиях лучше, конечно, не становиться низкостатусным павианом (именно эту мысль я пытаюсь как можно чаще доносить до сознания своих детей – особенно сына). Более значительный месседж заключается в том, что регрессионный анализ, пожалуй, – самый важный из имеющихся в распоряжении исследователей инструментов для поиска значимых закономерностей и связей в крупных совокупностях данных. Как правило, у нас нет возможности проводить управляемые эксперименты для получения данных о дискриминации на работе или выявления факторов, вызывающих развитие сердечно-сосудистых заболеваний. Источником наших представлений об этих и многих других социально значимых проблемах являются статистические инструменты, о которых шла речь в этой главе. В сущности, не будет преувеличением сказать, что значительная часть всех важных исследований, выполненных в области социальных наук за последние полстолетия (особенно после появления сравнительно недорогих компьютеров), проводилась с применением регрессионного анализа.

Регрессионный анализ представляет собой важную разновидность научного метода исследований; благодаря ему мы стали более здоровыми, защищенными и информированными людьми.

Какие же потенциальные ловушки подстерегают нас при использовании столь мощного и впечатляющего инструмента? Об этом я расскажу в следующей главе.