8. Центральная предельная теорема
Леброн Джеймс статистики

Порой статистика подобна магии. Она позволяет делать далекоидущие важные выводы на основе относительно небольшого объема данных. Каким-то образом нам удается предсказать исход президентских выборов, опросив лишь тысячу избирателей. Или, проверив на птицефабрике сотню куриных тушек на наличие сальмонеллы, оценить, исходя из этой информации, общее санитарное состояние предприятия.

Что же является источником столь необычайной силы обобщения? Это центральная предельная теорема, значение которой для статистики соизмеримо со значением Леброна Джеймса для профессионального баскетбола. Центральная предельная теорема – «источник энергии» для многих статистических действий, предполагающих использование той или иной выборки для получения выводов относительно некой более крупной совокупности данных (например, опрос населения или тест на наличие сальмонеллы). Хотя порой такого рода выводы могут казаться мистическими, фактически это просто сочетание двух инструментов, уже рассмотренных нами в этой книге: теории вероятностей и правильного формирования выборки. Прежде чем приступить к подробному рассмотрению механизма (на самом деле не такого уж сложного) центральной предельной теоремы, ознакомьтесь с примером, который поможет вам на интуитивном уровне понять, о чем пойдет речь.

Допустим, вы живете в городе, где будет проходить марафон. В нем примут участие бегуны со всего мира, а значит, многие из них не говорят по-английски. Чтобы своевременно и с максимальным комфортом доставить спортсменов к месту старта, всем участникам необходимо зарегистрироваться утром в день забега, после чего их произвольным образом рассадят по автобусам и отвезут на старт. К сожалению, один из автобусов затерялся где-то в пути. (Ладно, вам придется предположить, что ни у одного из его пассажиров не было мобильного телефона, а у водителя не оказалось GPS-навигатора; если не хотите заниматься утомительными математическими выкладками, всегда держите мобильный телефон при себе.) Будучи одним из общественных активистов города, вы подключаетесь к поискам пропавшего автобуса.

Вам повезло: вы натыкаетесь на какой-то сломавшийся автобус неподалеку от своего дома; возле автобуса коротает время группа расстроенных пассажиров, причем ни один из них не говорит по-английски. Наверное, это и есть тот автобус, который вы разыскиваете! У вас появляется шанс стать героем дня. Правда, вас смущает одно обстоятельство: пассажиры автобуса – слишком упитанные люди. Окинув эту группу взглядом, вы заключаете, что средний вес ее пассажиров превышает 220 фунтов. Трудно представить, что в случайно сформированной группе бегунов-марафонцев могут оказаться столь колоритные экземпляры. Вы звоните по мобильному телефону в штаб-квартиру поисковой команды и сообщаете: «Мне кажется, это не тот автобус, который мы ищем. Продолжайте поиск».

Дальнейший анализ подтверждает ваше первоначальное предположение. Когда на место прибывает переводчик, оказывается, что сломавшийся автобус направлялся на Международный фестиваль любителей сосисок, который также проводится в вашем городе, причем в тот же день, что и марафонский забег. (Для большего правдоподобия замечу, что участники фестивалей любителей сосисок нередко ходят в спортивных брюках свободного покроя, которые не стесняют их движений.)

Примите мои поздравления! Если вам понятно, каким образом человек, просто окинув беглым взглядом группу пассажиров автобуса и оценив их вес, может прийти к выводу, что конечным пунктом назначения этого автобуса вряд ли может быть место старта марафонского забега, значит, на интуитивном уровне вы уже постигли базовую идею центральной предельной теоремы. И все, что вам остается, это уяснить некоторые детали. А если вы понимаете центральную предельную теорему, то и большинство форм статистических выводов наверняка покажутся вам интуитивно понятными.

Базовый принцип, лежащий в основе центральной предельной теоремы, заключается в том, что большая, надлежащим образом сформированная выборка будет похожа на совокупность, из которой она извлечена. Разумеется, от выборки к выборке будут наблюдаться определенные вариации (например, группа пассажиров в каждом автобусе, направляющемся к месту старта марафонского забега, будет несколько отличаться от группы пассажиров в других автобусах), однако вероятность того, что какая-либо выборка будет существенно разниться с генеральной совокупностью, крайне низка. Именно эта логика позволила вам прийти к указанному выше интуитивному умозаключению, когда вы подошли к сломавшемуся автобусу и беглым взглядом оценили средний вес его пассажиров. Да, марафонскую дистанцию нередко бегут люди довольно плотного телосложения; среди участников каждого крупного марафона немало спортсменов, вес которых превышает 200 фунтов. Однако большинство бегунов-марафонцев – худощавые люди. Таким образом, вероятность того, что столь значительное число упитанных бегунов по случайному стечению обстоятельств окажется в одном автобусе, чрезвычайно мала. Вы могли бы вполне уверенно заключить, что встретившийся вам автобус перевозит не марафонцев. Конечно, не исключено, что вы ошибаетесь, однако, согласно теории вероятностей, шансы на ошибку в данном случае очень и очень невелики.

В этом и состоит интуитивная основа центральной предельной теоремы. Воспользовавшись кое-какими статистическими «прибамбасами», можно вычислить вероятность того, окажетесь ли вы правы или неправы. Например, мы можем подсчитать, что в случае, когда речь идет о 10 000 участниках марафонского забега, средний вес которых равняется 155 фунтов, вероятность того, что средний вес случайной выборки из 60 таких бегунов (примерная вместимость одного автобуса) окажется не ниже 220 фунтов, составляет менее одного шанса из 100. Давайте на данном этапе доверимся интуиции; впоследствии у нас будет немало возможностей выполнить соответствующие вычисления.

Центральная предельная теорема позволяет нам сделать перечисленные ниже выводы (их мы детально проанализируем в следующей главе).

1. Располагая подробными сведениями о какой-то совокупности, мы можем сделать далекоидущие выводы о любой надлежащим образом сформированной из нее выборке. Допустим, например, что у директора школы есть детальная информация о результатах сдачи стандартизованного теста всеми учащимися школы (среднее значение, среднеквадратическое отклонение и т. д.). Это значимые характеристики всей совокупности. Теперь предположим, что на следующей неделе ожидается прибытие некоего чиновника окружного управления образования, который намерен провести такой же стандартизованный тест для 100 случайным образом отобранных учеников. Результаты, продемонстрированные этой выборкой учащихся, будут использованы для оценки качества преподавания в данной школе.

Может ли директор школы с уверенностью утверждать, что баллы этих 100 произвольно отобранных учеников будут точно отражать результаты всех учащихся данной школы при сдаче этого теста? Вполне. Согласно центральной предельной теореме, средний тестовый балл группы из 100 учащихся, как правило, не будет существенно отличаться от среднего балла всех учеников данной школы.

2. Располагая подробными сведениями о какой-либо надлежащим образом сформированной выборке (среднее значение и среднеквадратическое отклонение), мы можем сделать чрезвычайно точные выводы относительно совокупности, из которой эта выборка была получена. По сути, это обратный вариант ситуации, которую мы рассматривали в приведенном выше примере. Иными словами, мы должны поставить себя на место чиновника окружного управления образования, который оценивает школы в своем округе. В отличие от директора школы, этот чиновник не располагает результатами (или не доверяет им) сдачи стандартизованного теста всеми учащимися конкретной школы. Вместо этого он проводит в каждой школе аналогичный тест для произвольной выборки из 100 учеников.

Может ли этот чиновник быть уверен, что качество преподавания в какой-либо конкретной школе в целом можно точно оценить, основываясь на результатах сдачи стандартизованного теста группой из 100 учащихся соответствующей школы? Да, может. Центральная предельная теорема гласит, что достаточно большая выборка, как правило, не будет существенно отличаться от генеральной совокупности, а это означает, что результаты, продемонстрированные этой выборкой (то есть баллы 100 случайным образом отобранных учащихся), с достаточной степенью точности отражают результаты соответствующей совокупности в целом (то есть баллы всех учащихся конкретной школы). Разумеется, именно на таком принципе строятся все опросы. Методологически правильный опрос 1200 человек может многое поведать о настроениях всего населения страны.

Итак, если сказанное выше в п. 1 верно, то сказанное в п. 2 также должно быть верно, и наоборот. Если какая-то выборка, как правило, хорошо отражает совокупность, из которой она была сформирована, то верно и обратное: совокупность, как правило, будет похожа на выборку, сформированную из нее. (Если дети похожи на своих родителей, то и родители должны быть похожи на своих детей.)

3. Наличие данных о какой-то конкретной выборке и данных о какой-то конкретной совокупности позволяет определить, согласуется ли эта выборка с другой выборкой, которая, возможно, получена из той же совокупности. Здесь речь идет, по сути, о примере с пропавшим автобусом, приведенном в начале главы. Нам известен (приблизительно) средний вес участников марафона. Нам также известен (приблизительно) средний вес пассажиров сломавшегося автобуса. Центральная предельная теорема позволяет нам вычислить вероятность того, что конкретная выборка (упитанные люди в автобусе) была сформирована из данной совокупности (участники марафонского забега). Если эта вероятность невелика, то с высокой степенью уверенности можно заключить, что данная выборка сформирована не из интересующей нас совокупности (например, люди в автобусе отнюдь не похожи на группу бегунов-марафонцев, направляющихся к месту старта).

4. Наконец, если нам известны исходные характеристики двух выборок, то мы можем определить, сформированы ли они из одной и той же совокупности. Вернемся еще раз к становящемуся все более абсурдным примеру с автобусом. Теперь нам известно, что марафонский забег будет проводиться в данном городе – равно как и Международный фестиваль любителей сосисок. Допустим, что в обеих группах тысячи участников и обе наняли десятки автобусов, в каждый из которых поместили произвольные выборки либо бегунов-марафонцев, либо поглотителей сосисок. Допустим также, что при перевозке участников этих мероприятий столкнулись два автобуса. (Я уже признал абсурдность своего примера, поэтому сценарий развития событий не должен вас удивлять. Просто продолжайте спокойно читать дальше.) Будучи, как было сказано выше, одним из видных общественных активистов в городе, вы прибываете на место происшествия и пытаетесь определить, ехали ли оба автобуса на одно и то же мероприятие (фестиваль любителей сосисок или марафонский забег). К несчастью, никто из пострадавших не говорит по-английски, но врачи скорой помощи, оперативно прибывшие на место происшествия, сообщают вам подробную информацию о весе каждого из пассажиров в столкнувшихся автобусах.

Основываясь лишь на этих сведениях, вы можете заключить, куда направлялись эти автобусы: на одно и то же мероприятие или на два разных. Как и прежде, положимся на интуицию. Допустим, что средний вес пассажиров в одном автобусе равняется 157 фунтам при среднеквадратическом (стандартном) отклонении 11 фунтов (это означает, что вес значительной части пассажиров находится в диапазоне от 146 до 168 фунтов). Теперь предположим, что средний вес пассажиров второго автобуса составляет 211 фунтов при среднеквадратическом отклонении 21 фунт (это означает, что вес значительной части пассажиров находится в диапазоне от 190 до 232 фунтов). Забудем на какое-то время о статистических формулах и будем опираться исключительно на логику: представляется ли вам вполне вероятным, что пассажиры обоих автобусов были случайным образом извлечены из одной и той же совокупности?

Вовсе нет. Более вероятным кажется то, что в одном из двух автобусов ехали бегуны-марафонцы, а в другом – любители сосисок. Помимо ощутимой разницы в показателях среднего веса пассажиров двух автобусов, нетрудно также заметить, что разброс в весе между этими двумя автобусами очень велик по сравнению с разбросом в весе в каждом из двух автобусов. Максимальный вес людей в «худощавом» автобусе (168 фунтов, что на одно среднеквадратическое отклонение больше среднего значения) меньше, чем минимальный вес людей в «упитанном» автобусе (190 фунтов, что на одно среднеквадратическое отклонение меньше среднего значения). Это верный признак (как со статистический, так и с логической точки зрения) того, что две выборки сформированы, скорее всего, из разных совокупностей.

Если на интуитивном уровне все это представляется вам вполне логичным, то вы уже на 93,2 % приблизились к пониманию сути центральной предельной теоремы. Чтобы придать этому интуитивному выводу некую техническую солидность, нам необходимо продвинуться еще на один шаг вперед. Очевидно, когда вы заглядываете в поломанный автобус и видите там группу довольно упитанных людей в спортивных брюках свободного покроя, у вас тотчас же мелькает догадка, что вряд ли это бегуны на марафонские дистанции. Центральная предельная теорема позволяет нам подвести под свои предположения солидную теоретическую базу и придать им определенную степень уверенности.

Например, исходя из неких базовых вычислений я могу заключить, что в 99 случаях из 100 средний вес пассажиров любого случайным образом выбранного автобуса с бегунами будет отличаться не более чем на девять фунтов от среднего веса всех зарегистрированных участников марафона. Именно это служит статистическим подтверждением моей догадки, когда я натыкаюсь на поломанный автобус с людьми. Средний вес его пассажиров на двадцать один фунт превышает средний вес всех зарегистрированных участников марафона, а это значит, что вероятность принадлежности пассажиров этого автобуса к составу участников забега не превышает 1 шанс из 100. Это позволяет мне с 99-процентной уверенностью отвергнуть гипотезу о том, что встретившийся мне автобус перевозил спортсменов (иными словами, я могу рассчитывать на то, что сделанный мною вывод окажется правильным в 99 случаях из 100).

Правда, согласно теории вероятностей, в среднем я окажусь неправ в 1 случае из 100.

Анализ такого рода целиком следует из центральной предельной теоремы, которая, с точки зрения статистики, обладает такой же мощью и элегантностью, как действия Леброна Джеймса на баскетбольной площадке. Согласно центральной предельной теореме, средние значения выборок для любой совокупности будут распределены относительно ее среднего значения примерно по нормальному закону. Ниже я постараюсь разъяснить это положение.

1. Допустим, у нас есть некая совокупность, например все зарегистрированные участники марафона, и нас интересует вес каждого бегуна. Любая выборка участников марафона (например шестидесят бегунов, перевозимых каждым автобусом) будет характеризоваться средним значением их веса.

2. Если делать повторные выборки из всего состава зарегистрированных участников марафона, например формировать случайным образом группы из шестидесяти бегунов, то каждая из этих выборок будет характеризоваться собственным средним значением веса. Это и будут средние значения выборок.

3. Большинство этих средних значений будут очень близки к среднему значению веса для данной совокупности. Какие-то из них окажутся чуть больше, какие-то – чуть меньше. По чистой случайности лишь очень немногие из них будут существенно превышать или быть ниже среднего значения веса для данной совокупности.

Прислушайтесь к этой музыке, поскольку именно сейчас все звуки сливаются в мощное крещендо…

4. Центральная предельная теорема гласит, что эти средние значения выборок будут распределены относительно среднего значения совокупности примерно по нормальному закону. Нормальное распределение, как вы, наверное, помните из главы 2, представляет собой распределение колоколообразной формы (например, величины веса взрослых мужчин), в котором 68 % наблюдений находятся на расстоянии одного среднеквадратического отклонения от среднего значения, 95 % наблюдений – на расстоянии двух среднеквадратических отклонений и т. д.

5. Все эти утверждения будут истинными, как бы ни выглядело распределение исходной совокупности. Чтобы средние значения выборок были распределены по нормальному закону, вовсе не обязательно, чтобы совокупность, из которой получены эти выборки, имела нормальное распределение.

Рассмотрим реальные данные, например распределение семейного дохода в Соединенных Штатах. Семейный доход в США не распределен по нормальному закону, а, как правило, скошен вправо. В любом данном году никакая из семей не может заработать меньше 0 долларов, поэтому у данного распределения должна быть нижняя граница. Между тем, годовые доходы у какой-то небольшой группы семей могут быть очень велики – сотни миллионов, а в отдельных случаях даже миллиарды долларов. В результате можно ожидать, что распределение семейного дохода в стране будет характеризоваться длинным «хвостом» справа, нечто наподобие этого:

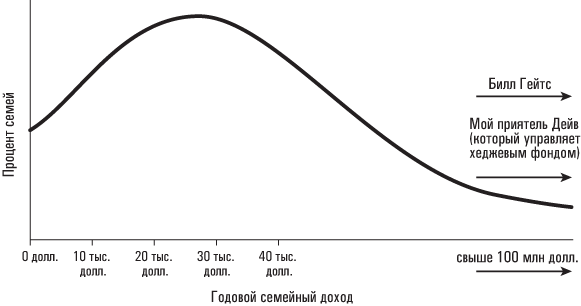
Медиана семейного дохода в Соединенных Штатах составляет примерно 51 900 долларов; средний семейный доход – 70 900 долларов. (Люди вроде Билла Гейтса сдвигают средний семейный доход вправо; вспомните последствия появления Билла Гейтса в баре, о которых рассказывалось в главе 2.) Теперь допустим, что мы берем случайную выборку из 1000 американских семей и собираем данные об их годовом семейном доходе. Что можно сказать об этой выборке, основываясь на приведенной выше информации и центральной предельной теореме?

Оказывается, довольно много. Прежде всего, можно подтвердить наше предположение о том, что среднее значение любой выборки будет равняться среднему значению совокупности, из которой такая выборка сформирована. Сущность репрезентативной выборки заключается в том, что она похожа на совокупность, из которой сформирована. Любая надлежащим образом созданная выборка не будет в среднем отличаться от Америки в целом. В такую выборку войдут и менеджеры хеджевых фондов, и бездомные, и полицейские, и все прочие основные группы населения, причем все они будут включены в выборку приблизительно в той пропорции, в какой представлены в соответствующей совокупности. Следовательно, можно ожидать, что средний семейный доход в репрезентативной выборке из 1000 американских семей приблизительно составит 70 900 долларов. Будет ли он в точности равен 70 900 долларам? Нет. Но существенно отличаться от этой суммы не будет.

Если мы возьмем несколько выборок из 1000 американских семей, то предположительно их средние значения будут гуппироваться вокруг среднего значения данной совокупности, то есть 70 900 долларов. Можно ожидать, что некоторые из средних значений будут несколько выше этой суммы, а другие – несколько ниже. Может ли среди этих выборок оказаться такая, у которой средний семейный доход составит 427 000 долларов? Разумеется да, однако это очень и очень маловероятно. (Не забывайте, что мы используем правильную методологию формирования выборок, иными словами, не проводим опрос на парковке возле Greenwich Country Club.) Столь же маловероятно, что средний семейный доход в надлежащим образом сформированной выборке из 1000 американских семей составит 8000 долларов.

Все наши рассуждения основываются на простейшей логике. Центральная предельная теорема позволяет пойти еще дальше, описывая ожидаемое распределение средних значений разных выборок, группирующихся вблизи среднего значения генеральной совокупности. А именно, средние значения этих выборок вблизи среднего значения нашей совокупности (в данном случае 70 900 долларов) распределены по нормальному закону. Вспомните, что форма распределения исходной совокупности значения не имеет. Распределение семейного дохода в Соединенных Штатах характеризуется значительным скосом, однако у распределения средних значений выборок скос отсутствует. Если бы мы взяли 100 разных выборок, каждая из которых включает 1000 семей, и построили график частоты наших результатов, то можно было бы ожидать, что средние значения этих выборок образуют хорошо знакомое нам «колоколообразное» распределение в районе 70 900 долларов.

Чем больше количество выборок, тем точнее это распределение аппроксимируется нормальным распределением. А чем больше размер каждой выборки, тем такое распределение будет уже. Чтобы проверить этот результат, давайте проведем эксперимент с реальными данными о весе реальных американцев. Мичиганский университет выполнил повторное исследование под названием Americans’ Changing Lives («Меняющаяся жизнь американцев»), которое предусматривает детальные наблюдения за несколькими тысячами взрослых американцев, в том числе и за их весом. Распределение веса слегка скошено вправо, поскольку биологически легче весить на 100 фунтов больше нормы, чем на 100 фунтов меньше нормы. Средний вес для всех взрослых в этом исследовании составляет 162 фунта.

С помощью компьютера и базового статистического программного обеспечения можно создать на основе данных Americans’ Changing Lives произвольную выборку из 100 человек. Вообще говоря, это можно делать многократно, чтобы увидеть, как полученные результаты согласуются с тем, что предсказывает нам центральная предельная теорема. Ниже приведен график распределения 100 средних значений выборок (с округлением до ближайшего фунта), сгенерированных случайным образом на основе данных Americans’ Changing Lives.

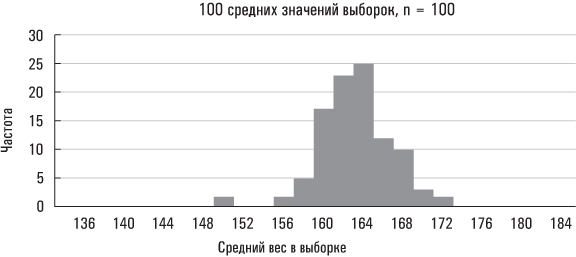
Чем больше размер выборки и чем больше выборок, тем точнее распределение их средних значений аппроксимируется нормальным распределением. (Чтобы обеспечить применимость центральной предельной теоремы, желательно, чтобы размер выборки был не менее 30.) Это должно быть понятно на интуитивном уровне. Большой размер выборки в меньшей степени подвержен случайным отклонениям. Выборка же из 2 человек может быть сильно скошена, если в ней окажется человек с необычайно большим (или слишком малым) весом. Напротив, на выборку из 500 человек лишь очень незначительно повлияет наличие в ней нескольких человек с нестандартным весом.

Итак, мы очень близки к тому, чтобы воплотить в жизнь все свои статистические мечты! Средние значения выборок распределены приблизительно по нормальному закону, как описано выше. Эффективность нормального распределения является следствием нашей информированности о том, какая примерно доля наблюдений окажется выше или ниже среднего значения на расстоянии, не превышающем одного среднеквадратического отклонения (68 %); на расстоянии, не превышающем двух среднеквадратических отклонений (95 %), и т. д. Это очень важная для нас информация.

Ранее в этой главе я указывал на возможность интуитивного вывода о том, что автобус с пассажирами, средний вес которых на двадцать пять фунтов превышает средний вес всех зарегистрированных участников марафона, вряд ли может быть потерявшимся автобусом с его участниками. Чтобы получить численное подтверждение своей интуитивной догадки – то есть иметь основания утверждать, что этот вывод окажется правильным в 95 (или в 99, или в 99,9) процентах случаев, – нам необходима еще одна техническая характеристика – стандартная (среднеквадратическая) ошибка.

Стандартная ошибка измеряет разброс средних значений выборок. Насколько предположительно близко они будут группироваться вокруг среднего значения совокупности? Здесь возможна некоторая путаница, поскольку вам уже известны два разных показателя разброса: среднеквадратическое (стандартное) отклонение и стандартная (среднеквадратическая) ошибка. Чтобы внести ясность в этот вопрос, нужно учитывать следующее.

1. Среднеквадратическое отклонение измеряет разброс в исходной совокупности. В данном случае оно может измерять разброс значения веса всех участников Framingham Heart Study, то есть разброс вблизи среднего значения для всех зарегистрированных участников марафона.

2. Стандартная ошибка измеряет разброс средних значений выборок. Если мы извлекли ряд выборок (в каждой по 100 значений) из Framingham Heart Study, то как будет выглядеть разброс их средних значений?

3. Вот что связывает между собой эти две концепции: стандартная ошибка является среднеквадратическим отклонением средних значений выборок! Замечательно, не правда ли?

Большая стандартная ошибка означает, что средние значения выборок разбросаны на значительных расстояниях от среднего значения совокупности; малая стандартная ошибка означает, что средние значения выборок располагаются относительно близко вокруг среднего значения совокупности. Ниже приведены три реальных примера на основе данных Americans’ Changing Lives.

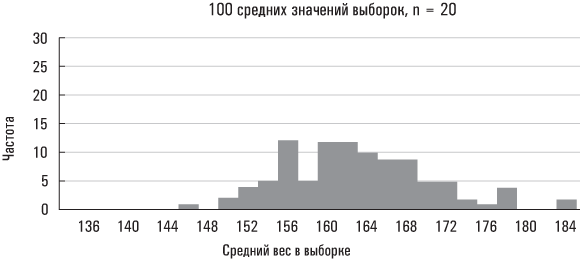
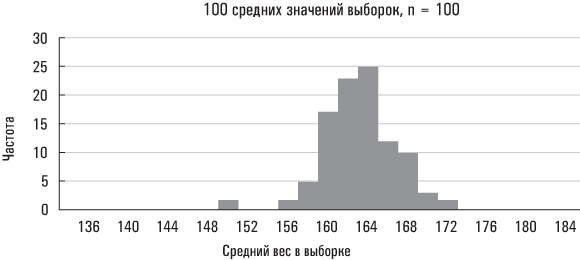
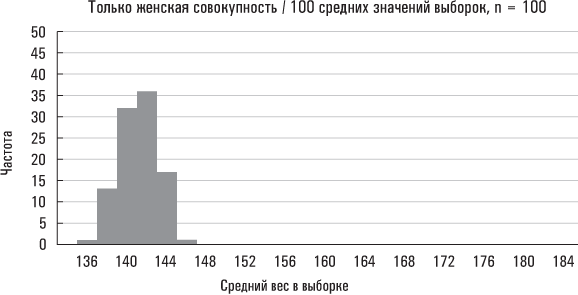
Второе распределение, размер выборки у которого больше, сгруппировано вблизи среднего значения плотнее, чем первое. Больший размер выборки снижает вероятность того, что ее среднее значение существенно отклонится от среднего значения совокупности. Последний набор средних значений выборок получен из подмножества рассматриваемой нами совокупности (в данном случае таким подмножеством являются женщины). Поскольку значения веса женщин в этой совокупности данных разбросаны в меньшей степени, чем значения веса всех лиц в рассматриваемой нами совокупности, вполне естественно, что вес выборок, сформированных исключительно из женской совокупности, должен быть менее разбросанным, чем выборок, извлеченных из всей совокупности Americans’ Changing Lives. (Эти выборки также сгруппированы вблизи несколько отличающегося среднего значения совокупности, так как средний вес всех женщин в исследовании Americans’ Changing Lives разнится со средним весом всей совокупности, охваченной данным экспериментом.)

Нарисованная мной картина носит универсальный характер. Средние значения выборок будут группироваться вблизи среднего значения совокупности более плотно по мере увеличения размера каждой выборки (например средние значения наших выборок группировались вблизи среднего значения совокупности более плотно, когда их размер увеличился с 20 до 100). И менее плотно, когда исходная совокупность окажется более «разбросанной» (например средние значения наших выборок для всей совокупности Americans’ Changing Lives были более разбросанными, чем средние значения выборок лишь для женской совокупности).

Если вам до сих пор удавалось следить за логикой моего изложения, то формула для стандартной ошибки (SE) не потребует дополнительных разъяснений: SE = s ÷ √n, где s – среднеквадратическое отклонение для совокупности, из которой сформирована данная выборка, а n – размер выборки. Не следует, однако, слишком уповать на формулы. Не забывайте привлекать на помощь интуицию. Стандартная ошибка будет большой, когда среднеквадратическое отклонение исходного распределения велико. Большая выборка, сформированная из сильно разбросанной совокупности, также, скорее всего, окажется сильно разбросанной; большая выборка, сформированная из совокупности, плотно сгруппированной вблизи среднего значения, также, скорее всего, окажется плотно сгруппированной вблизи среднего значения. Если вернуться к примеру с весом, то можно ожидать, что стандартная ошибка для выборки, извлеченной из всей совокупности Americans’ Changing Lives, будет большей, чем стандартная ошибка для выборки, состоящей только из мужчин в возрасте от двадцати до тридцати лет. Именно поэтому среднеквадратическое отклонение (s) находится в числителе приведенной выше формулы.

Аналогично можно ожидать, что стандартная ошибка будет уменьшаться по мере увеличения размера выборки, поскольку большие выборки в меньшей степени подвержены искажению со стороны экстремальных наблюдений («отщепенцев»). Именно поэтому размер выборки n находится в знаменателе формулы. (Разъяснение причины, по которой в формуле используется корень квадратный из n, мы оставим для более «продвинутых» учебников по статистике; в данном случае для нас важны базовые соотношения.)

В случае данных Americans’ Changing Lives нам фактически известно среднеквадратическое отклонение этой совокупности, однако зачастую так не бывает. В отношении крупных выборок мы можем предположить, что их среднеквадратическое отклонение довольно близко к среднеквадратическому отклонению генеральной совокупности.

Наконец, настало время подвести итог сказанному. Поскольку средние значения выборок распределены по нормальному закону (благодаря центральной предельной теореме), мы можем воспользоваться богатым потенциалом кривой нормального распределения. Мы рассчитываем, что примерно 68 % средних значений всех выборок будут отстоять от среднего значения совокупности на расстоянии, не превышающем одной стандартной ошибки; 95 % – на расстоянии, не превышающем двух стандартных ошибок; и 99,7 % – на расстоянии, не превышающем трех стандартных ошибок.

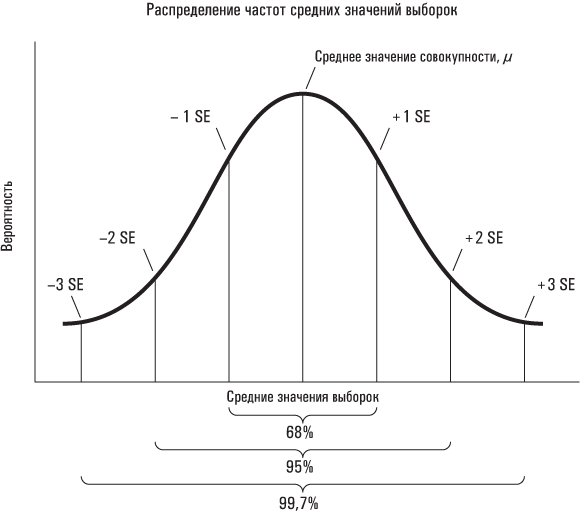
Теперь вернемся к отклонению (разбросу) в примере с пропавшим автобусом – правда, на этот раз призовем на помощь не интуицию, а числа. (Сам по себе этот пример остается абсурдным; в следующей главе мы рассмотрим множество более близких к реальности случаев.) Допустим, что организаторы исследования Americans’ Changing Lives пригласили всех его участников на выходные в Бостон, чтобы весело провести время и заодно предоставить кое-какие недостающие данные. Участников распределяют произвольным образом по автобусам и отвозят в тестовый центр, где их взвесят, определят рост и т. п. К ужасу организаторов мероприятия, один из автобусов пропадает где-то по пути в тестовый центр. Об этом событии оповещают в программе новостей местного радио и телевидения. Возвращаясь примерно в то же время в своем автомобиле с Фестиваля любителей сосисок, вы замечаете на обочине дороги сломавшийся автобус. Похоже, его водитель был вынужден резко свернуть в сторону, пытаясь уклониться от столкновения с лосем, неожиданно появившимся на дороге. От столь резкого маневра все пассажиры потеряли сознание или лишились дара речи, хотя никто из них, к счастью, не получил серьезных травм. (Такое предположение понадобилось мне исключительно для чистоты приведенного здесь примера, а надежда на отсутствие у пассажиров серьезных травм объясняется моим врожденным человеколюбием.) Врачи кареты скорой помощи, оперативно прибывшие на место происшествия, сообщили вам, что средний вес 62 пассажиров автобуса составляет 194 фунта. Кроме того, оказалось (к огромному облегчению всех любителей животных), что лось, от столкновения с которым пытался увернуться водитель автобуса, практически не пострадал (если не считать легкого ушиба задней ноги), но от сильного испуга тоже потерял сознание и лежит рядом с автобусом.

К счастью, вам известен средний вес пассажиров автобуса, а также среднеквадратическое отклонение для всей совокупности Americans’ Changing Lives. Кроме того, мы имеем общее представление о центральной предельной теореме и знаем, как оказать первую помощь пострадавшему животному. Средний вес участников исследования Americans’ Changing Lives составляет 162 фунта; среднеквадратическое отклонение равняется 36. На основе этой информации вы можете вычислить стандартную ошибку для выборки из 62 человек (количество пассажиров автобуса, потерявших сознание): s / √62 = 36/7,9, или 4,6.

Разница между средним значением этой выборки (194 фунта) и средним значением совокупности (162 фунта) равна 32 фунта, то есть значительно больше трех стандартных ошибок. Из центральной предельной теоремы вам известно, что 99,7 % средних значений всех выборок будут отстоять от среднего значения совокупности на расстоянии, не превышающем трех стандартных ошибок. Таким образом, крайне маловероятно, что встретившийся вам автобус перевозит группу участников исследования Americans’ Changing Lives. Будучи видным общественным активистом города, вы звоните организаторам мероприятия, чтобы сообщить, что в повстречавшемся вам автобусе, скорее всего, находится какая-то другая группа людей. Правда, в этом случае вы можете опираться на статистические результаты, а не свои «интуитивные догадки». Вы сообщаете организаторам, что отрицаете вероятность того, что найденный вами автобус именно тот, который они разыскивают, с 99,7 % доверительным уровнем. А поскольку в данном случае вы разговариваете с людьми, знакомыми со статистикой, то можете не сомневаться, они понимают, что вы правы. (Всегда приятно иметь дело с умными людьми!)

Сделанные вами выводы находят дальнейшее подтверждение, когда врачи скорой помощи берут пробы крови у пассажиров автобуса и обнаруживают, что средний уровень холестерина в их крови превышает средний уровень холестерина в крови участников исследования Americans’ Changing Lives на пять стандартных ошибок. Из этого следует, что впавшие в бессознательное состояние пассажиры – участники Фестиваля любителей сосисок. (Впоследствии это было неопровержимо доказано.)

[У этой истории оказался счастливый конец. Когда к пассажирам автобуса вернулось сознание, организаторы исследования Americans’ Changing Lives посоветовали им проконсультироваться у специалистов-диетологов относительно опасности употребления в пищу продуктов с высоким содержанием насыщенных жиров. После таких консультаций многие из любителей сосисок решили порвать со своим позорным прошлым и вернуться к более здоровому рациону питания. Пострадавшего лося выходили в местной ветеринарной клинике и выпустили на свободу под одобрительные возгласы членов местного Общества защиты животных. Да, история почему-то умалчивает о судьбе водителя автобуса. Возможно, потому, что статистика не занимается судьбами отдельно взятых людей. Лось – совсем другое дело, замолчать его судьбу не удастся! В случае чего за него может вступиться Общество защиты животных.]

В этой главе я пытался говорить только об основах. Вы, наверное, обратили внимание, что центральная предельная теорема применима лишь в случаях, когда размер выборки достаточно велик (как правило, не менее 30). Кроме того, нам требуется относительно большая выборка, если мы намерены предположить, что ее среднеквадратическое отклонение будет примерно таким же, как и среднеквадратическое отклонение генеральной совокупности. Существует немало статистических поправок, которые можно применять в случае несоблюдения указанных условий, но все это похоже на сахарную глазурь на торте (и, возможно, даже на шоколадные крошки, которыми присыпают эту глазурь сверху). «Общая картина» здесь проста и чрезвычайно эффективна.

1. Если вы формируете на основе какой-либо совокупности большие (по объему) случайные выборки, то их средние значения будут распределены по нормальному закону вблизи среднего значения соответствующей совокупности (какой бы вид ни имело распределение исходной совокупности).

2. Большинство средних значений выборок будет расположено достаточно близко к среднему значению совокупности (что именно следует в том или ином случае считать «достаточно близким», определяется стандартной ошибкой).

3. Центральная предельная теорема говорит нам о вероятности того, что среднее значение выборки будет находиться не дальше определенного расстояния от среднего значения совокупности. Относительно маловероятно, что среднее значение выборки будет отстоять от среднего значения совокупности дальше, чем на расстояние двух стандартных ошибок, и крайне маловероятно, что среднее значение выборки будет отстоять от среднего значения совокупности дальше, чем на расстояние трех и более стандартных ошибок.

4. Чем меньше вероятность того, что какой-то исход оказался чисто случайным, тем больше мы можем быть уверены в том, что здесь не обошлось без воздействия какого-то другого фактора.

В этом по большому счету и заключается сущность статистического вывода. Центральная предельная теорема главным образом делает все это возможным. И до тех пор, пока Леброн Джеймс не станет столько раз чемпионом НБА, сколько Майкл Джордан (шесть), центральная предельная теорема будет производить на нас гораздо большее впечатление, чем знаменитый баскетболист.