3.3. Функция «цена-отклик»

Назад: 3.2. Анализ релевантной ценовой информации

Дальше: 3.4. Эмпирическое определение функции «цена-отклик»

3.3.1. Классификация функций «цена-отклик»

Кривая спроса, которая также называется функцией «цена-отклик», описывает функциональную зависимость между ценой p и объемом продаж, или количеством q:

q = q(p). (3.1)

Цена – это независимая переменная, а объем продаж – зависимая переменная. В учебниках по экономике во многих случаях приводится функция зеркального отображения p = p(q), где объем является независимой переменной, а цена – зависимой.

Такая функция спроса основана на представлении о том, что поставщик предлагает определенное количество товара, а рынок определяет цену. На современных неоднородных рынках функция, выраженная формулой (3.1), более реалистична.

Функция «цена-отклик» – необходимое условие ценовой оптимизации. На практике знание функции «цена-отклик» зачастую ограничено и имеет высокую погрешность. Функции «цена-отклик» можно классифицировать по следующим критериям.

• Уровень укрупнения. Индивидуальные или укрупненные функции «цена-отклик». Индивидуальная функция описывает, как меняется спрос отдельных потребителей в зависимости от цены. Укрупненная форма показывает изменение спроса (по всем покупателям) как функции цены.

• Форма рынка. Здесь проводится разграничение между монопольными и конкурентными рынками. При монополии уровень спроса зависит единственно от цены, устанавливаемой монополистом. При конкуренции цены конкурентов влияют на объемы продаж компании и, следовательно, должны быть включены в качестве независимых переменных в функцию «цена-отклик».

• Форма. Функции «цена-отклик» можно выразить в табличной или графической форме или в виде математической формулы.

• Источники информации. Данные, используемые для определения функции «цена-отклик», можно получить из таких источников, как экспертное суждение, опросы клиентов, эксперименты или рыночная информация.

3.3.2. Функции «цена-отклик» и ценовая эластичность

3.3.2.1. Индивидуальные и укрупненные функции «цена-отклик»

Начнем с рассмотрения индивидуальной функции «цена-отклик». Затем из них будем выводить укрупненные функции.

Имея дело с индивидуальным спросом, необходимо разграничить два случая.

• Товары длительного пользования. Кривая спроса отражает решение «да-нет» каждого отдельного потребителя. Мы назовем это случаем «да-нет». Люди приобретают одну стиральную машину, один смартфон, одну видеокамеру или один ноутбук. Или не приобретают их вообще.

• Потребительские товары. В этом случае люди часто покупают несколько единиц товара за один раз, в зависимости от цены. Мы назовем это случаем «переменное количество». Под эту категорию подпадают продукты питания, например, йогурт или прохладительные напитки, а также услуги, к примеру, поход в кино. Если цена ниже, отдельный покупатель приобретает больше и потребляет чаще.

В левой части рис. 3.3 представлен случай «да-нет». Клиент делает покупку, если цена ниже, чем (субъективно воспринимаемая) ценность товара. Самая высокая цена, которую клиент готов заплатить за продукт, соотносится с его субъективной ценностью. Мы будем называть ее «максимальная цена» (в экономической литературе ее также называют резервированной или запретительной ценой).

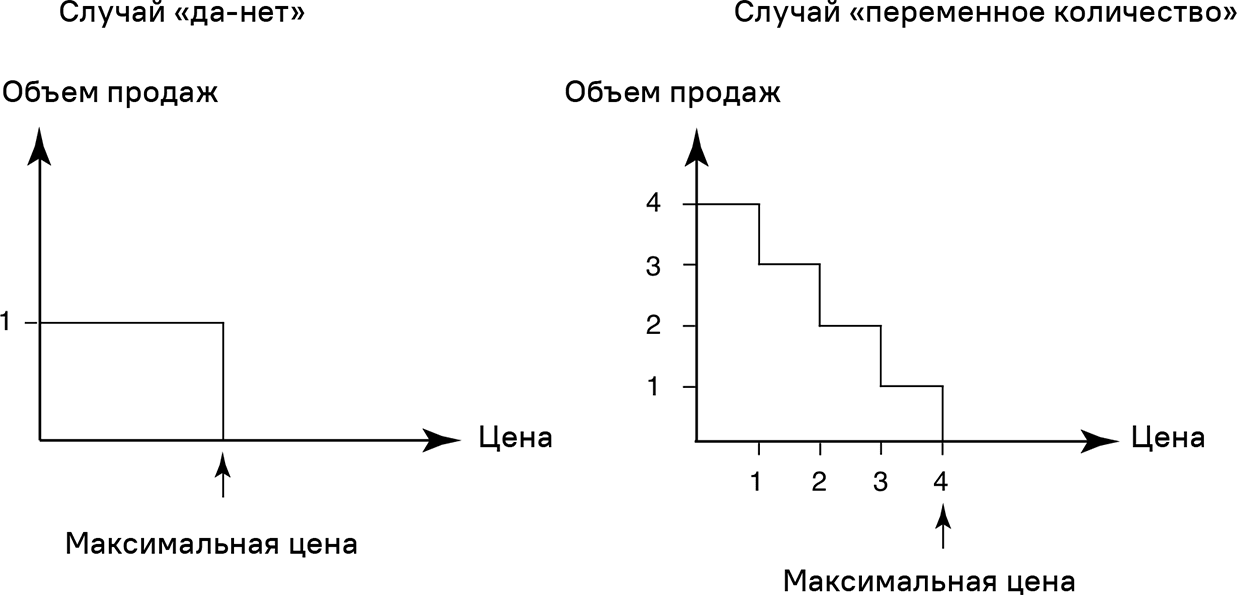
Рис. 3.3. Индивидуальные функции «цена-отклик» для случаев «да-нет» и «переменное количество»

В случае «переменное количество» клиент аналогичным образом сравнивает цену и ценность каждой единицы продукта. Как можно видеть в правой части рис. 3.3, клиент готов потратить $4 на первую единицу продукта, но только $3 на вторую. Такое снижение готовности платить следует второму закону Госсена [12], который гласит, что предельная полезность (или «предельная потребительская ценность») снижается с увеличением потребления продукта. Вторая, третья и четвертая единицы продукта добавляют меньше полезности, чем предыдущие. Следствие для случая «переменное количество»: чем выше цена, тем меньшее количество отдельный потребитель может купить. Лучше всего рассматривать случай «переменное количество» как серию случаев «да-нет». Потребитель принимает решение «да-нет» для каждой последовательной единицы товара на основе субъективной ценности добавочной единицы.

Когда цены устанавливаются на индивидуальной основе, предпосылки для двух случаев различны. В случае «да-нет» продавец стремится выяснить, какую максимальную цену готов заплатить отдельный клиент, и называть именно эту цену. Это главная проблема ценообразования, когда цены обсуждаются с каждым покупателем в индивидуальном порядке. В случае «переменное количество» есть два варианта. Можно либо установить одинаковую цену за единицу товара, вне зависимости от приобретаемого объема, или провести дифференциацию цен по этому критерию. Последний вариант называется «нелинейное ценообразование». В случае «переменное количество» нужно знать предельную полезность каждой единицы продукта, чтобы иметь возможность определить индивидуальные функции «цена-отклик».

3.3.2.2. Укрупненная функция «цена-отклик»

Укрупненная функция «цена-отклик» получается сложением объемов по каждой цене и всем клиентам. Клиенты могут быть однородны и неоднородны. На практике они практически всегда неоднородны. Это означает, что у них будут разные максимальные цены.

На рис. 3.4 мы предполагаем неоднородность и показываем укрупнение по трем потребителям для случаев «да-нет» и «переменное количество».

В обоих случаях укрупненная функция «цена-отклик» имеет отрицательный уклон, то есть приобретается меньше единиц товара по высоким ценам. Если мы включим сюда большее количество потребителей, очертания функции будут приближены к непрерывной кривой.

3.3.2.3. Определение ценовой эластичности

Влияние цены на объем продаж измеряется ценовой эластичностью.

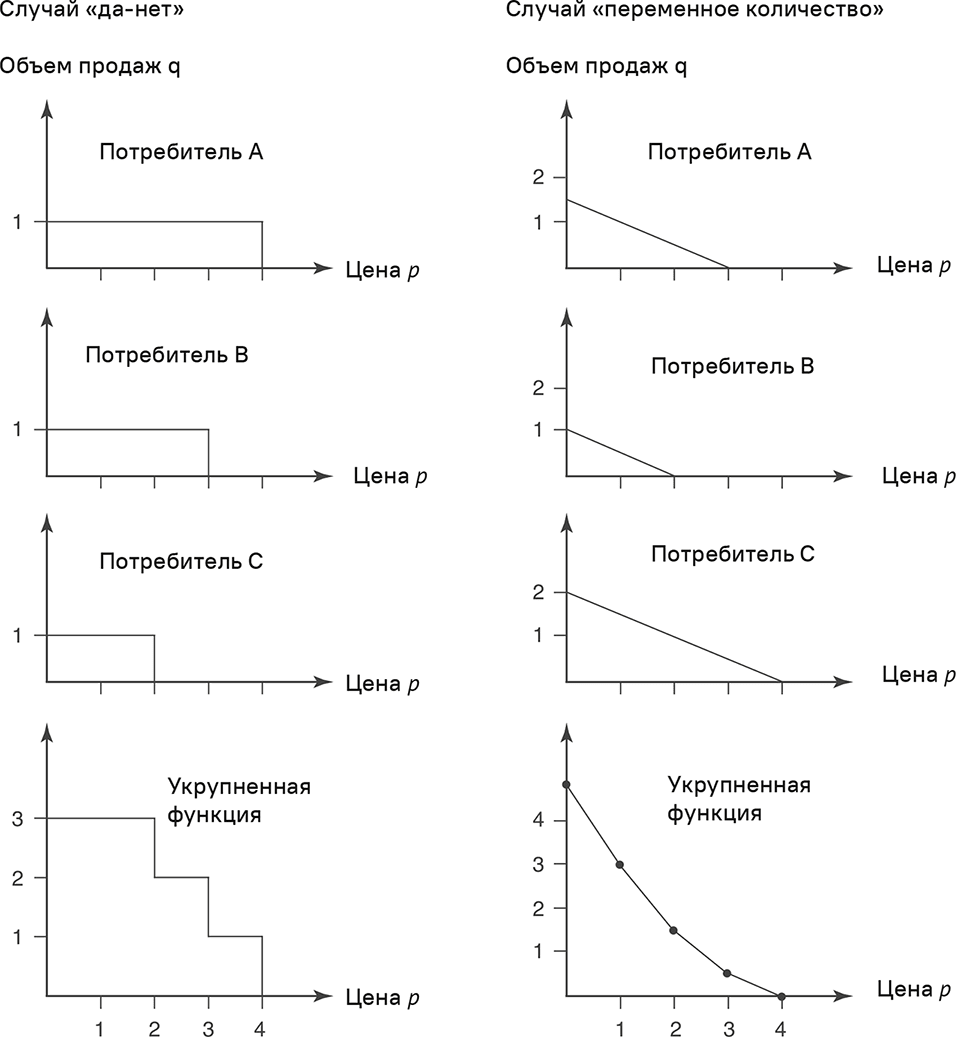
Рис. 3.4. Укрупнение индивидуальных функций «цена-отклик» для трех различных потребителей

Эластичность – это отношение относительного изменения одной переменной к относительному изменению переменной, которая служит причиной изменения. Эластичность не имеет размерности. Ценовая эластичность определяется следующим образом:

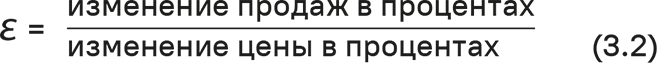
Если снижение цены на 10 % приводит к расширению объемов на 20 %, ценовая эластичность имеет значение –2. Знак отрицания указывает, что изменения цены и объема имеют противоположную направленность. Ценовая эластичность –2 говорит о том, что относительное изменение объема продаж вдвое превышает относительное изменение цены. Для бесконечно малых изменений ценовая эластичность математически определяется как:

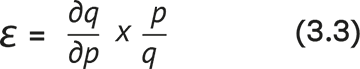
где – (дq ÷ дp) это первая производная функции «цена-отклик», q = q(p), q – объем, p – цена.

3.3.2.4. Линейные функции «цена-отклик» и ценовая эластичность на монопольном рынке

Линейная зависимость объема q от цены p – это простейшее условие:

На рис. 3.5 показана линейная функция «цена-отклик» на монопольном рынке. Параметра – это отсекаемый отрезок на оси объема, который показывает максимальный объем (по нулевой цене). Отношение a/b определяет цену, при которой объем равен нулю. Данная цена соответствует отсекаемому отрезку на оси цены. Это (совокупная) максимальная цена.

Параметр b – это уклон функции «цена-отклик». Иными словами, он показывает изменение объема, вызванное изменением цены одной единицы продукта. Чем больше b, тем чувствительнее объем реагирует на изменения цены. Поскольку уклон линейной функции – это константа, изменение объема при определенном изменении цены всегда одинаково. Оно не зависит от предыдущего ценового уровня. Ценовая эластичность линейной функции равна ε = −bp/(a – bp). Это отрицательная величина, но когда заходит речь о ценовой эластичности, она часто выражается в виде ее абсолютного значения. Для линейной функции «цена-отклик» ценовая эластичность следует модели, показанной на рис. 3.5. Ее абсолютное значение бывает очень большим, если цены высокие и прибижаются к максимальному уровню.

Самое крупное преимущество линейной функции «цена-отклик» заключается в ее простоте и легкости интерпретации. Чтобы определить функцию, нужно спрогнозировать всего два параметра a и b. Далее мы покажем, что эта функция обозначает простые правила принятия ценовых решений. С другой стороны, линейной функции недостает теоретической базы. Как следует из утверждения ниже, она появилась в теоретическом вакууме: «Вполне корректно как провести прямую линию, так и использовать любую другую форму» [13].

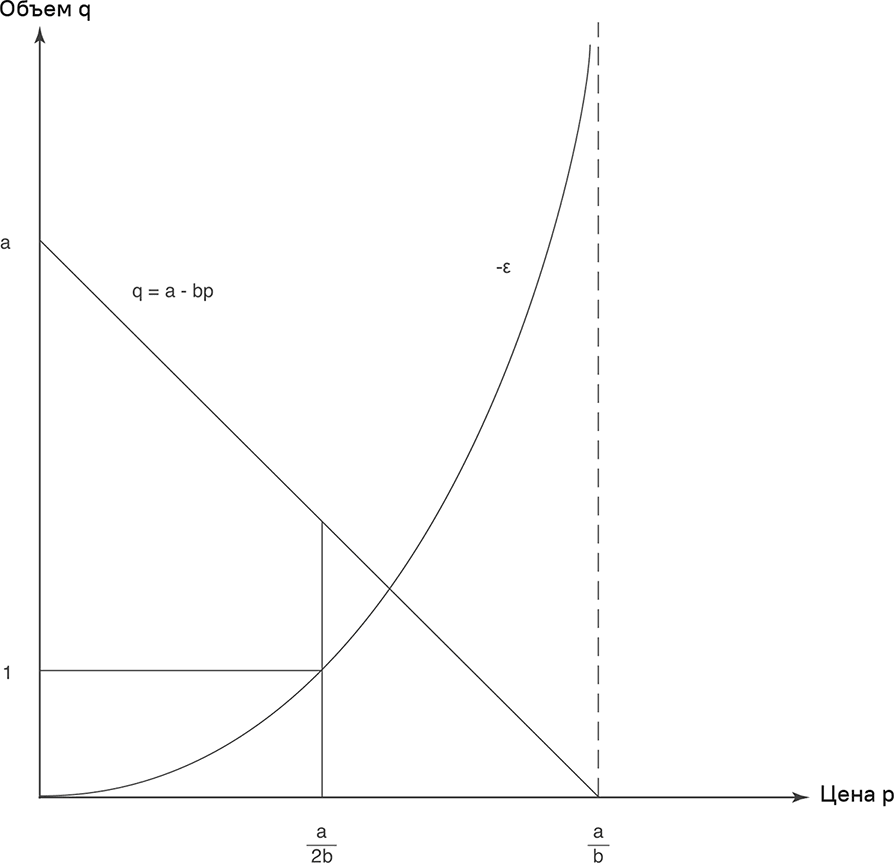
Рис. 3.5. Линейная функция «цена-отклик» (монополия)

Несмотря на свою простоту, линейная функция зачастую вполне подходит для эмпирических данных. Исходя из собственного опыта, мы рекомендуем использовать ее только в ситуациях, когда рассматриваемый ценовой интервал не слишком отклоняется от диапазона текущих или предыдущих цен. При больших изменениях цены линейная модель может привести к ошибочным выводам. В разумных пределах, однако, она работает не хуже, чем более сложные модели. Здесь применима максима «если сомневаешься – упрощай».

3.3.2.5. Линейные функции «цена-отклик» и ценовая эластичность на конкурентном рынке

На конкурентном рынке в функцию «цена-отклик» следует включить такие переменные, как доля рынка, относительная цена или ценовая разница.

Независимые переменные

Помимо собственной цены p_i, нужно принять во внимание цены конкурентов в качестве независимых перменных. В табл. 3.1 представлены некоторые варианты того, как это сделать.

Таблица 3.1. Альтернативные практические варианты независимых переменных в функции «цена-отклик» на конкурентном рынке

Альтернативный вариант 1 требует очень тщательного анализа и, как правило, исключается из рассмотрения из-за проблем с мультиколлинеарностью, то есть нельзя изолировать влияние каждой отдельной цены. Варианты со 2-го по 4-й требуют определения средней цены p. Можно сделать это без взвешивания или использовать доли рынка как весовые факторы. Kucher [14] показал, что средние цены, взвешенные по доле рынка, обладают более высоким поясняющим качеством, статистической значимостью и экономическим правдоподобием.

Влияние цен конкурентов на собственный объем измеряется перекрестной эластичностью цен. Перекрестная эластичность цен квантифицирует влияние цен конкурентов на собственный объем:

Или в случае бесконечно малых величин:

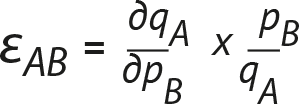
Перекрестная эластичность цен отражает процентное изменение объема qA продукта А, когда цена pВ продукта В меняется на 1 %. Если А и В являются заменяющими величинами, то есть продукты напрямую конкурируют (к примеру, Ford Focus и Honda Civic), перекрестная эластичность цен положительная. Если конкурент снижает цену на 10 %, а собственный объем падает на 5 %, перекрестная эластичность цен равна +0,5. Здесь знак положительный, поскольку оба изменения (цены конкурента и собственного падения объема) движутся в одном направлении. Если оба продукта дополняют друг друга (например, принтеры и картриджи), перекрестная эластичность цен, как прямая ценовая эластичность в формуле (3.2), отрицательная.

Есть несколько способов определить зависимую переменную на конкрентном рынке. Зависимой переменной может быть либо объем q_i, либо рыночная доля m_i продукта i. Если мы примем Q как общий объем на выбранном рынке, две переменные будут относиться дру к другу следующим образом:

m_i = q_i/Q, соответственно q_i = m_i х Q.

Для ценовой эластичности объема q_i и доли рынка m_i получим следующее уравнение:

εq_i = Ценовая эластичность общего спроса Q + ценовая эластичность доли рынка m_i.

Мы можем использовать объем q_i или долю рынка m_i как взаимозаменяемые зависимые переменные только в том случае, если ценовая эластичность общего спроса Q равна нулю. Если Q в действительности зависит от цены, нам понадобятся две функции «цена-отклик» (одна для общего спроса Q, а вторая для доли рынка m_i). Обе субмодели можно рассматривать отдельно или в рамках одной модели, которая учитывает влияние цены на объем q_i. При определении зависимых переменных нужно внимательно оценить, какие переменные испытывают влияние цены. Давать общие рекомендации относительно определения независимых переменных не имеет смысла. В каждом отдельном случае необходимо анализировать различные варианты. Только так можно построить достоверную функцию «цена-отклик».

3.3.3. Дополнительные формы функции «цена-отклик»

Помимо линейной модели, есть три формы функций «цена-отклик», применимые на конкурентном рынке: мультипликативная функция, функция притяжения и модель Гутенберга, показанные в табл. 3.2.

3.3.3.1. Мультипликативная модель

Основной причиной применения мультипликативной модели является ее простота и тот факт, что коэффициент b можно интерпретировать как постоянную цену или перекрестную эластичность цены. В мультипликативной функции «цена-отклик», представленной на рис. 3.6, относительная цена (собственная цена/цена конкурента) служит независимой переменной. Экспонента b измеряет ценовую эластичность, которая не зависит от ценового уровня. Эта модель имеет постоянную ценовую эластичность, которая также равна перекрестной эластичности цен. Главное достоинство мультипликативной модели – ее простота. Если посмотреть с практической стороны, постоянная ценовая эластичность упрощает рассуждения. Но, как и в случае линейной функции «цена-отклик», она не имеет теоретической базы.

При этом постоянная ценовая эластичность мультипликативной модели не очень хорошо отражает действительность. Кажется не слишком реалистичным, что объем не снижается до нуля даже при очень высоких ценах. В отличие от линейной модели, максимальной цены здесь не существует. Поэтому можно скептически относиться к ситуации, когда мультипликативная модель показывает существенный люфт повышения цен.

Таблица 3.2. Формулы функций «цена-отклик» (конкуренция)

Существует серьезное подозрение, что данная модель в целом недооценивает ценовую эластичность, по крайней мере, в более высоких ценовых диапазонах. Действительно, в эмпирических оценках мультипликативной модели часто существуют (постоянные) ценовые эластичности с абсолютным значением меньше единицы, что не имеет смысла с точки зрения ценовой оптимизации. Такая ситуация означала бы, что любое повышение цены должно вести к более высоким прибылям. Исходя из собственного опыта, мы считаем мультипликативную модель менее надежной, чем линейную. Ее можно применять только в узких интервалах вокруг текущей цены.

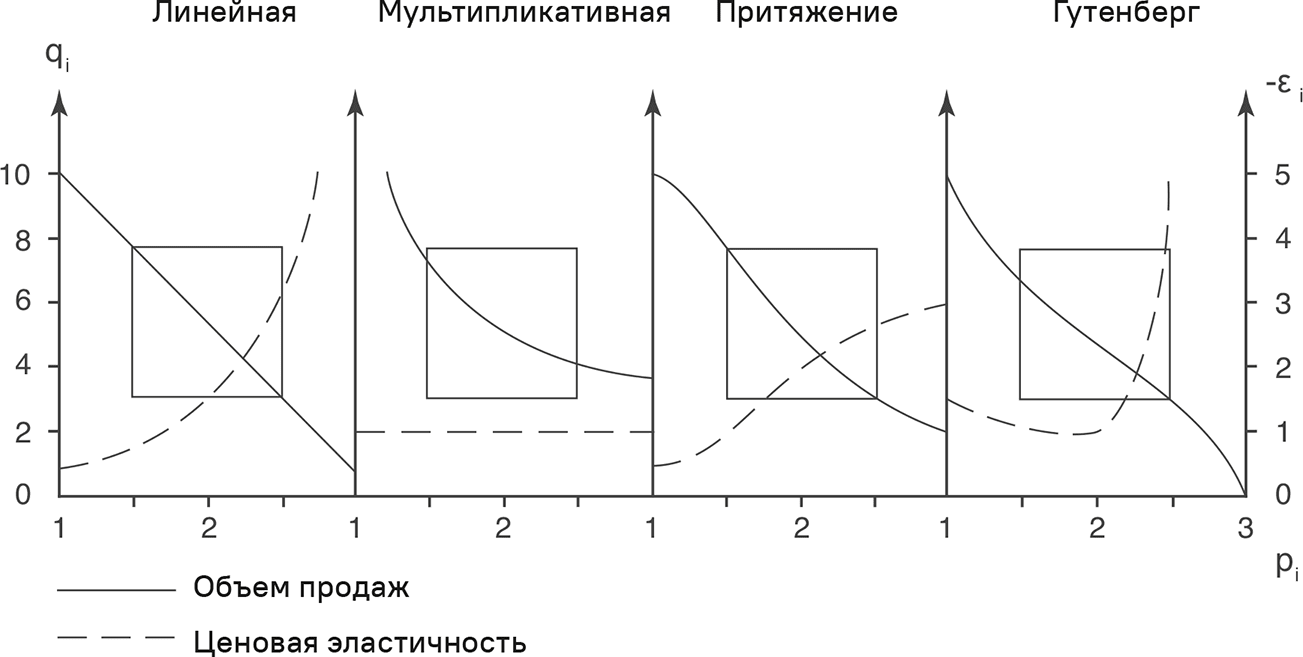
Рис. 3.6. Функции «цена-отклик» на конкурентных рынках

3.3.3.2. Модель притяжения

В отличие от двух предыдущих моделей, модель притяжения имеет явные корни в теории бихевиоризма. Она исходит из утверждения, что доля рынка m_i продукта i определяется относительным притяжением продукта. Чтобы пояснить долю рынка m_i, используется отношение притяжения продукта i к сумме притяжений всех конкурирующих продуктов:

Доля рынка m_i = Притяжение продукта i / Сумма притяжений всех продуктов

«Притяжение» выводится из того факта, что данная модель изначально была разработана для описания эффекта притяжения атрибутов качества, рекламы и т. д. Мы можем интерпретировать притяжение как полезность или предпочтение. Цена определенно является атрибутом, отрицательно влияющим на притяжение. Достоинство модели притяжения заключается в ее логической целостности: все доли рынка mi находятся между 0 и 100 % и в сумме составляют 100 %. Вне зависимости от конкретной спецификации, модели притяжения рекомендованы к применению, когда включены дополнительные атрибуты продукта, помимо цены, которые измеряются уровнем их полезности или предпочтения. Это применимо, например, к совместному измерению. Модель притяжения допускает использовать полезность как основу для подсчета объема продаж, дохода и прибыли при альтернативных ценах.

С учетом влияния цены модель притяжения следует скептически оценивать на крайних уровнях. Как можно видеть на рис. 3.6, эффект изменения цены или ценовой разницы возле значения цены конкурента сравнительно сильный и ослабевает по мере удаления от этого значения. Данная концепция диаметрально противоположна модели Гутенберга, которая, как мы увидим в следующем разделе, имеет прочную эмпирическую достоверность. С учетом этого вывода и нашего собственного опыта мы рекомендуем использовать модель притяжения с большой осторожностью, когда предполагается устанавливать цены, сильно отличающиеся от существующих уровней. На крайних уровнях этой функции существует риск ошибки. Но если брать узкий ценовой диапазон, модель притяжения приемлема.

Вот еще одно эмпирическое наблюдение, хотя мы признаем, что для обобщения данных его недостаточно. По нашему опыту, лидер рынка часто обладает большей долей рынка, чем прогнозирует модель притяжения. Здесь, очевидно, имеет место «бонус рыночного лидера». Чтобы его скомпенсировать, мелкие конкуренты, как правило, располагают меньшими долями, чем прогнозирует модель.

3.3.3.3. Модель Гутенберга

Модель Гутенберга лучше всего известна как функция «цена-отклик» с двойным изломом. Gutenberg [11, 15], однако, рассматривал вариант с более постепенными переходами как эквивалент кривой с двойным изломом. Оба варианта представлены на рис. 3.7, где p̅_i представляет среднюю цену продуктов, конкурирующих с продуктом i.

Небольшие ценовые изменения или ценовые различия стимулируют лишь небольшие сдвиги потребителей от одного продукта к другому. Срединная, плоская часть функции «цена-отклик» называется «монополистический интервал», потому что напоминает функцию «цена-отклик» для монополиста.

Однако, согласно этой модели, в том случае «если цена снижается с увеличением расстояния между индивидуальной ценой продажи и средней ценой конкурентов, то количество покупателей, ранее приобретавших у конкурента, растет в соответствующей прогрессии». Если цена изменяется в сторону повышения, «степень флуктуации растет в той мере, в которой повышение цены отклоняется от первоначального уровня» [11].

Когда мы просим экспертов спрогнозировать объем продаж в достаточно широком ценовом диапазоне, результаты, как правило, следуют кривой Гутенберга. Менеджеры и эксперты обычно отмечают ценовой предел, вне которого изменения объема становятся заметно резче. Данный опыт подтверждает, что практики мыслят в терминах модели Гутенберга. Модель Гутенберга подтверждается реже при проведении эконометрического анализа рыночных данных. Возможно, это зависит от того факта, что диапазон эмпирически наблюдаемых ценовых флуктуаций слишком узок. Цены вне «монополистического интервала» обычно не держатся на рынках долго.

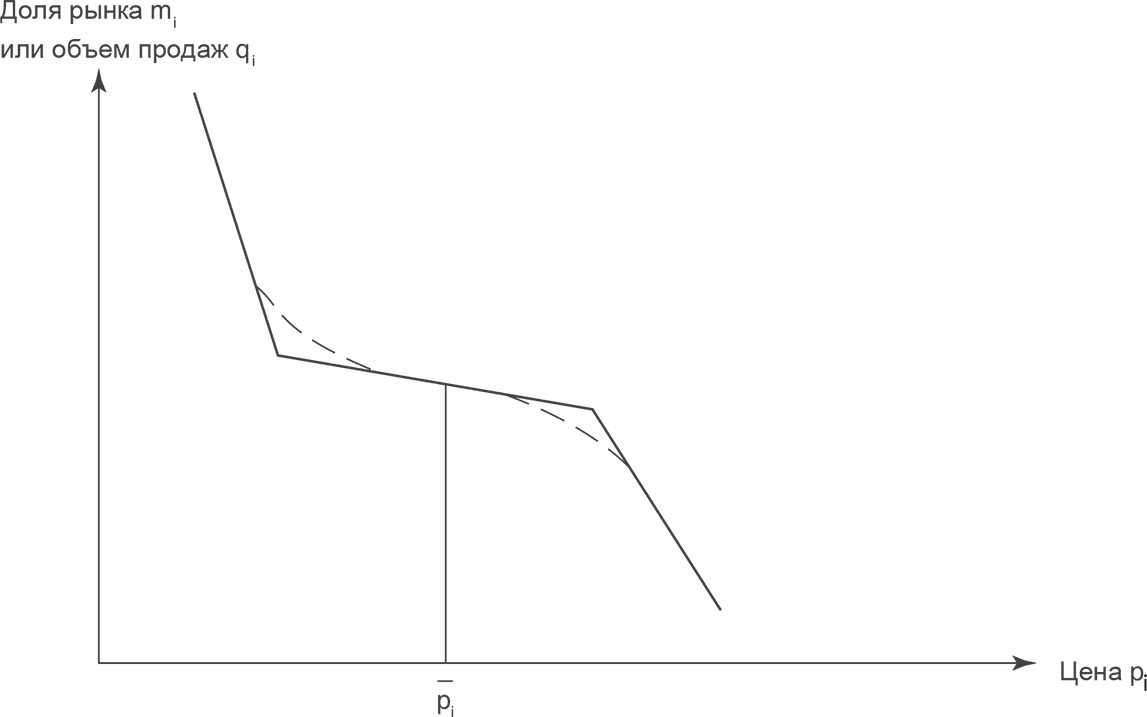
Рис. 3.7. Модель Гутенберга в форме двойного излома и непрерывной линии

3.3.4. Эмпирические выводы о ценовой эластичности

В силу особой важности ценовой эластичности в прайс-менеджменте это понятие стало предметом большого числа научных трудов. Хотя значения ценовой эластичности нелегко сравнивать по ряду причин, метаанализ Bijmolt et al. [16] позволяет сделать интересные наблюдения. В этом исследовании был рассмотрен 1851 прогноз ценовой эластичности на основе данных о покупках в секторе B2C. В своей книге «Эмпирические обобщения о влиянии маркетинга» Hanssens [17] считает эти прогнозы репрезентативными для потребительских товаров в упаковках. Распределение 1851 значения ценовой эластичности показано на рис. 3.8.

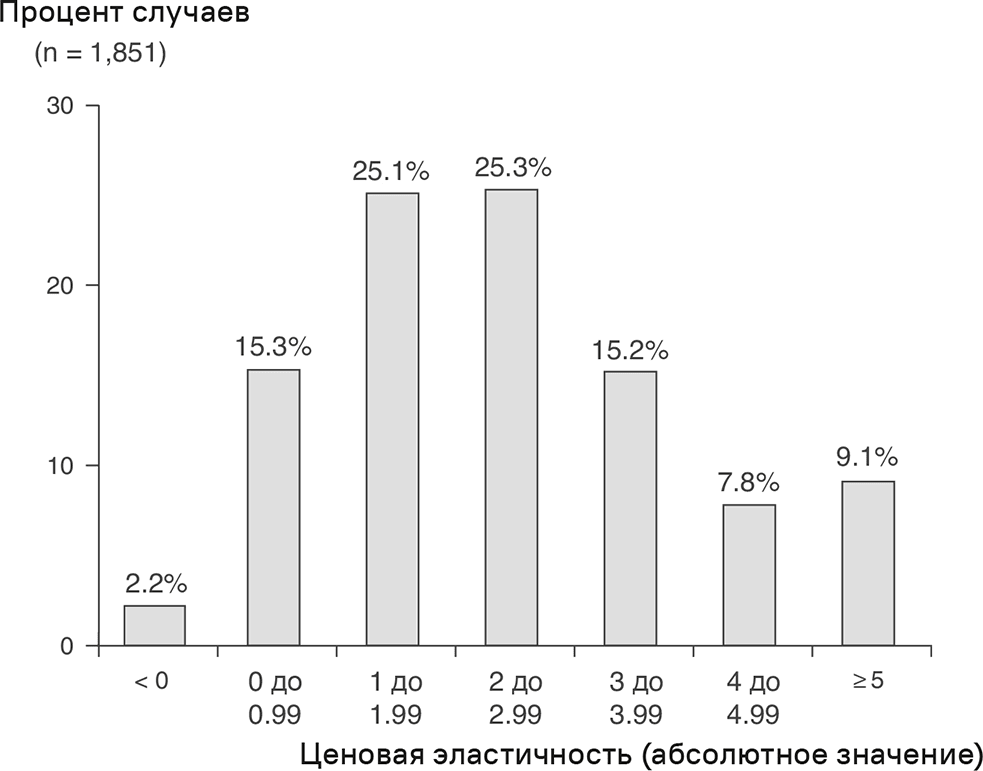
Рис. 3.8. Распределение эконометрических прогнозных значений ценовой эластичности

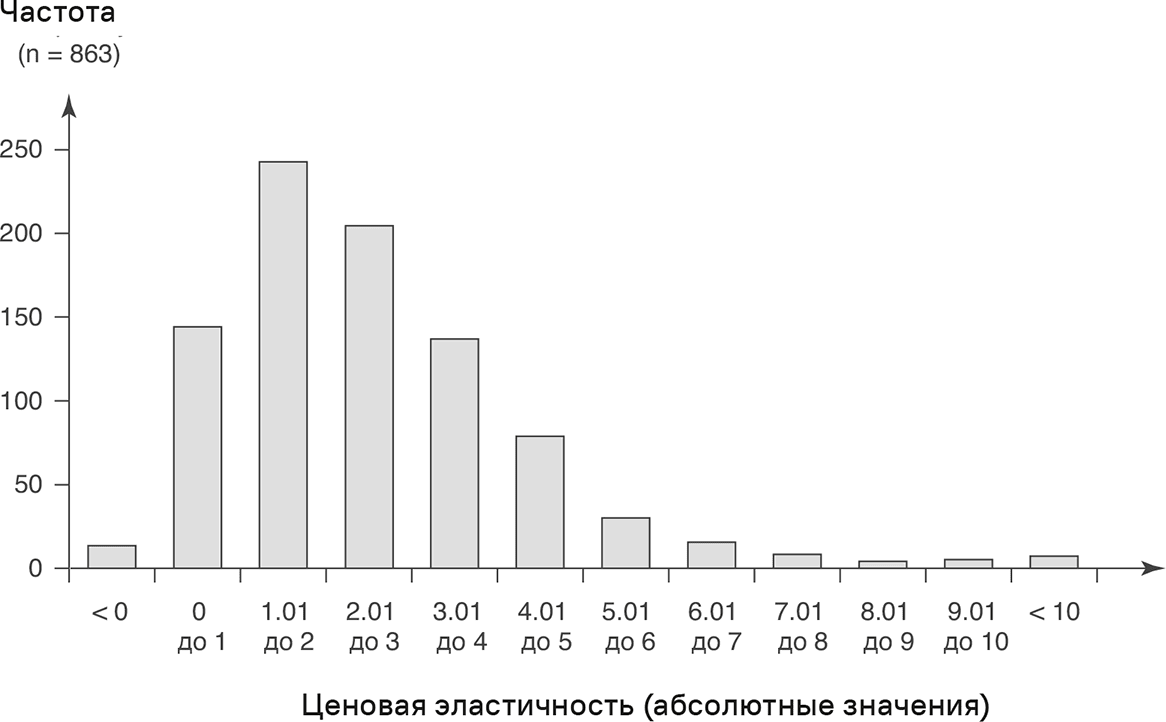
Рис. 3.9. Распределение эконометрически спрогнозированных значений ценовой эластичности (из научных публикаций) [18]

Среднее абсолютное значение прогнозов равно 2,62, медианное – 2,22. Медиана в данном контексте более значима, поскольку на нее не влияют резко выделяющиеся значения. На рис. 3.8 показано, что значения ценовой эластичности сильно разнятся.

В то время как данные по ценовой эластичности, собранные Bijmolt et al. [16], датируются годами с 1961-го по 2005-й, значения, показанные на рис. 3.9, основаны на более позднем метаанализе Friedel [18], чья работа представляет собой наиболее всеобъемлющую оценку эмпирической информации по ценовой эластичности на сегодняшний момент. В первом исследовании Фридель проанализировал 863 эмпирических значения, взятых из научных журналов с 1981 по 2006 годы. Ценовые эластичности из этой части метаанализа Фриделя дают среднее значение 2,51 и медианное 2,21. Совпадение между анализом Фриделя и выводами Bijmolt et al. [16] большое.

Во второй выборке Фридель использовал данные консалтинга. Распределение ценовых эластичностей, показанное на рис. 3.10, основано на консалтинговых проектах Simon-Kucher & Partners [18]. Данные проектов охватывают годы с 2003-го по 2007-й и включают 386 значений ценовой эластичности. Среднее абсолютное значение – 1,73, медианное – 1,29 [18]. Эти значения сильно отличаются от данных, использованных в литературе.

Данные Simon-Kucher & Partners охватывают очень широкий спектр продуктов и услуг – автомобили, фармацевтика, электроды, профессиональные приборы, страхование, косметика, кухонные принадлежности и т. д., в то время как метаанализ Bijmolt et al. [16] ограничивался быстро реализуемыми потребительскими товарами. Ценовые эластичности рассчитывались на основе повышения и снижения цен на 10 %, а потом выводилось среднее значение соответствующей эластичности. Можно сделать вывод, что эластичности при дисконтах и промоушн-акциях составляли основу набора данных Bijmolt et al. [16]. Они выше, чем долгосрочные ценовые эластичности, спрогнозированные в консалтинговых проектах, – этот вывод также подтверждает Hanssens [17].

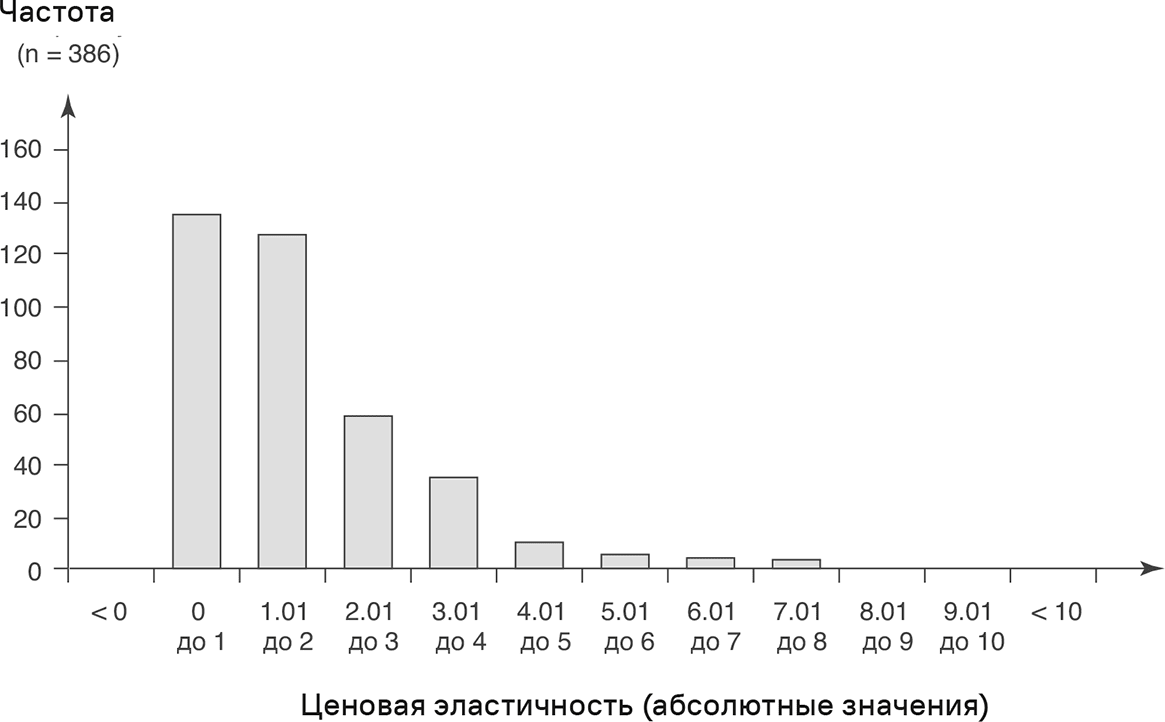
Рис. 3.10. Распределение ценовых эластичностей (консалтинговые проекты) [17]

Таблица 3.3. Сравнение ценовых эластичностей для понижения и повышения цен

В целом можно видеть, что различные товары, рассмотренные в консалтинговых проектах Simon-Kucher & Partners, имеют в среднем меньшие значения ценовой эластичности, чем быстро реализуемые потребительские товары. Это можно объяснить тем, что набор данных Simon-Kucher & Partners среди других товаров и услуг охватывает специальные промышленные товары, товары для охраны труда и здоровья, инновационные лекарства и предметы роскоши – у всех них относительно низкая ценовая эластичность.

Наконец, работа Фриделя [18] содержит дальнейшие выводы о воздействии повышения и понижения цен на основе набора данных Simon-Kucher & Partners. В табл. 3.3 мы видим средние и медианные значения 386 ценовых эластичностей при повышении и понижении цен. Средняя ценовая эластичность для снижения цен равнялась –1,62, для повышения –1,84. Медианная ценовая эластичность равнялась –1,07 для понижения цены и –1,50 для повышения. Согласно этим наблюдениям, объемы продаж сильнее реагируют на повышение, а не на понижение цен. Это расхождение можно объяснить различиями в моделях реагирования конкурентов.

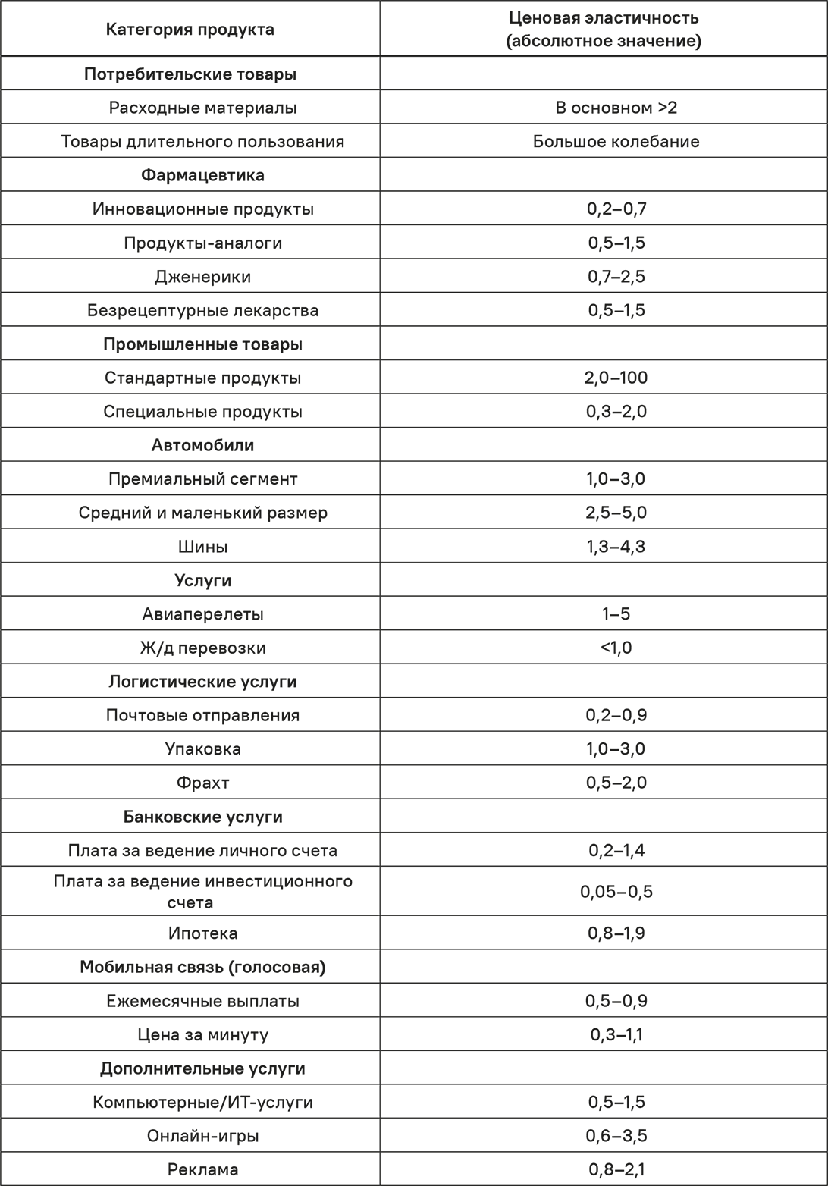
В табл. 3.4 дан обзор эмпирических ценовых эластичностей для различных категорий продуктов. Эту выборку нельзя считать репрезентативной или полной; скорее, она дает представление о широком диапазоне эмпирических ценовых эластичностей.

В некоторых случаях можно видеть очень высокие значения ценовой эластичности. В качестве примера можно привести марку сигарет, снижение цены на которую на 13,2 % обеспечило рост рыночной доли на 1300 %. Это соответствует значению абсолютной ценовой эластичности – почти 100. Для промышленных товаров разброс тоже может быть велик. В опросе производителей машинного оборудования респонденты оценивали свою ценовую эластичность значительно ниже единицы. В опросе экспертов компании – поставщика сырья респонденты ожидали, что повышение цены на 2 % вызовет падение объема продаж на 50 %. Это дает абсолютную ценовую эластичность 25.

В следующем примере мы обнаружили необычайно низкую ценовую эластичность. Это касается членских взносов в ADAC – немецком филиале Американской автомобильной ассоциации (AAA). В ADAC 19 млн членов – это крупнейший в Европе автомобильный клуб. После десятилетия стабильных цен ADAC повысил членские взносы [19]. Стоимость классического членства выросла на 10,1 % – с €44,50 до €49. Стоимость членства «Плюс» выросла на 13 % – с €79,50 до €89,50. Среднее повышение цены по всем категориям составило 12 %. Только 0,1 % членов, или 18 956 человек из всей членской базы в 18,92 млн, вышли из клуба в следующем году [20]. Ценовая эластичность по этим цифрам была –0,01 = (–0,1 %/12 %), то есть величина, стремящаяся к нулю. В одном исследовании рассматривались данные крупной компании такси для прогнозирования ценовых эластичностей. База данных включает почти 50 млн отдельных наблюдений. Диапазон ценовой эластичности здесь от –1,5 до –2 [21]. На этом примере показано, как Big Data (данные трансакций и запросов в Интернете) используются для прогнозирования ценовой эластичности.

Научная литература часто старается выявить условия, при которых ценовая эластичность бывает высокой или низкой. Большинство эмпирических экспериментов не дают четких результатов. Мы предупреждаем насчет генерализации ценовых эластичностей, потому что они в огромной степени зависят от атрибутов товара и специфического конкурентного окружения. К примеру, в одной работе высказывается предположение, что высококачественный продукт имеет сравнительно низкую ценовую эластичность. Интуитивно это утверждение кажется правдоподобным. Однако эмпирический анализ Фриделя [18] не поддерживает это допущение. На самом деле результаты анализа показывают, что продукты высокого качества проявляют высокую ценовую эластичность.

В исследовании Фриделя данный эффект наблюдается и при повышении цен, и при понижении, при этом в случае понижения эластичность выше [18].

Еще один драйвер ценовой эластичности – товарный бренд. Реакция на скидки у ведущих брендов намного сильнее, чем у менее желанных брендов во время промоушн-акций. Fong et al. [22] утверждают, что магазинные бренды имеют ценовую эластичность ниже, чем бренды ведущих производителей. Bijmolt et al. [16], однако, не заметили никакого значимого влияния бренда (магазинного или оригинального) на ценовую эластичность. Krishnamurthi и Raj [23] сделали вывод, что потребители, лояльные к определенному бренду, обладают более низкой ценовой эластичностью, чем нелояльные, когда речь заходит о выборе товара. Но в плане решения о том, сколько единиц товара купить, лояльные к бренду клиенты демонстрируют повышенную ценовую эластичность. Помимо качества и объемов продукта, влияние имеет продолжительность ценовой акции. Olbrich et al. [24] провели эмпирический анализ эффективности ценовых акций на продукты питания на длинном временном горизонте. Анализ показал, что влияние ценовых акций со временем снижается.

В дополнение к этим наблюдениям Фридель [18] сообщает, что степень отличия продукта компании от продуктов конкурентов оказывает значимое воздействие на его ценовую эластичность. Чем больше субъективные отличия продукта по ключевым атрибутам от продукта конкурентов, тем ниже устойчивость продукта и его ценовая эластичность [18]. Исследование Фриделя показывает, что это справедливо как для понижения цен, так и для их повышения [18].

Что касается субъективной сложности продукта как детерминанты ценовой эластичности, Фридель [18] сообщает об одинаковых результатах для повышения и понижения цен. В обоих случаях исследование поддерживает вывод о том, что высокая степень сложности снижает ценовую эластичность. Это объясняется тем, что цена играет второстепенную роль в решении о покупке сложных продуктов, и потребители обращают относительно мало внимания на цену по сравнению с другими атрибутами [18].

Направление ценового изменения влияет на удовлетворенность покупателя ценовой эластичностью. Koschate [25] обнаружил, что более довольные клиенты менее чувствительны к повышению цены. Неясно, однако, оказывает ли удовлетворенность клиентов смягчающий эффект при снижении цен.

Таблица 3.4. Эмпирическая выборка значений ценовой эластичности (Simon-Kucher & Partners)

Обзор

На основании данных литературы и большой проектной базы данных Simon-Kucher & Partners мы можем заключить, что ценовую эластичность повышают следующие атрибуты.

Характеристики продукта

• Высокая степень подобия и заменяемости конкурирующих продуктов; небольшая дифференциация.

• Большая частота покупок.

• Качество, позиционирование и распределение для массового рынка.

• Большая доля цены продукта в общей стоимости.

• Частое использование продукта во время акций; активная ценовая реклама.

• Низкий уровень сложности продукта.

• Единичный товар (в отличие от пакетных решений).

• Продукт стимулирует товарооборот у ритейлеров.

• Большая доля продукта, используемого в промоушн-акциях.

Характеристики рынка

• Высокое конкурентное давление во время продаж.

• Высокая ценовая прозрачность.

• Индустрия/сектор с низкой доходностью продаж.

• Сильное ценовое давление со стороны потребителей (закупка/приобретение).

• Высокая концентрация на уровне потребителей.

• Высокая доля интернет-торговли.

Характеристики потребителя

• Высокая ценовая осведомленность.

• Высокая готовность принять на себя риск.

• Хорошее знание продукта: способность объективно оценивать товары.

• Слабая/неразвитая осведомленность о бренде.

• Низкое значение имиджа и престижа.

• Низкая лояльность к бренду.

• Слабая осведомленность о качестве.

• Низкое значение удобства и возможности делать покупки в одном месте.

В конечном итоге ценовую эластичность необходимо определять в зависимости от конкретного случая. В научной литературе можно встретить некоторые заключения о ценовой эластичности, однако зачастую они неубедительны и даже противоречивы. Хотя результаты Фриделя [18] поддерживают наши утверждения об эмпирически спрогнозированных значениях ценовой эластичности и факторах влияния, мы предлагаем считать их отправной точкой и пользоваться для сведения, а не в качестве обобщений или универсальных правил.

Назад: 3.2. Анализ релевантной ценовой информации

Дальше: 3.4. Эмпирическое определение функции «цена-отклик»