Первоначально, в 1974 году, предположение Хокинга об излучении черных дыр было встречено скептически, но, как мы видели, постепенно большинство физиков признали эту мысль отнюдь не глупой. Если основные понятия общей теории относительности и квантовой механики верны, черные дыры просто обязаны иметь излучение, как всякий раскаленный объект. Первичных черных дыр пока обнаружить не удалось, но если бы они отыскались и оказалось, что они не испускают гамма-лучи и рентгеновские лучи, физики были бы неприятно озадачены.

Вспомним еще раз, какие частицы испускает черная дыра согласно теории Хокинга. На горизонте событий появляется пара частиц. Частица с отрицательной энергией падает в черную дыру. Поскольку ее энергия отрицательна, она не добавляется к энергии черной дыры, а вычитается из нее. Что происходит с энергией? (Мы же не допускаем, чтобы энергия попросту исчезла из мира.) Энергия уносится во внешний мир вместе с положительно заряженной частицей (см. главу 6).

В итоге, как вы помните, черная дыра теряет массу, и ее горизонт событий съеживается. Для первичной черной дыры история может закончиться тем, что она полностью исчезнет, и ее гибель, вероятно, будет сопровождаться весьма впечатляющим фейерверком. Но как может что-то выходить за пределы черной дыры, если из черной дыры ничего не исходит? То была одна из величайших детективных загадок на манер “запертой комнаты”, и сыщик С. Х. разгадал ее.

Вслед за идеей, что вещество в черной дыре, быть может, не приходит к абсолютному концу времени, стягиваясь в сингулярность, появилось подозрение насчет другой сингулярности, той, которую Хокинг поместил в начале времени. Квантовая теория открывала новые возможности: при Большом взрыве сингулярность могла быть и “размазана”, как выражался Хокинг. Значит, дверь не так уж плотно захлопнулась у нас перед носом.

Хокинг припомнил схожую проблему, с которой квантовой теории удалось справиться ранее. Проблема была связана с атомной моделью Резерфорда: “Модель предполагала, что вокруг центрального ядра вращаются электроны, словно планеты вокруг Солнца. И тут имелось затруднение” (вернитесь к рис. 2.1). “Классическая теория предсказывала, что движение электрона вызывает излучение световых волн. Эти волны отнимают у электрона энергию, и потому он по спирали спускается все ближе к ядру, пока не столкнется с ним”. Что-то в этой картине было неладно, ведь атомы не переживают подобный коллапс.

Спасла квантовая механика с ее принципом неопределенности. Невозможно одновременно установить и точную позицию, и точное движение электрона. “Если бы электрон упал на ядро, и его позиция, и характер движения были бы точно определены, – напоминает Хокинг. – Однако квантовая механика предсказывает отсутствие у электрона точно определенной позиции: вероятность обнаружить его размазана по определенной области вокруг ядра”. Электроны не спускаются внутрь по спирали и не падают на ядро. Атомного коллапса не происходит.

Согласно Хокингу, “предсказание классической общей теории относительности о сингулярности беспредельной плотности на момент Большого взрыва сродни предсказанию классической теории [о падении электрона на ядро]”. Утверждать, будто в момент Большого взрыва все находилось в одной точке бесконечной плотности или в черной дыре, – значит измерять с большей точностью, чем допускает принцип неопределенности. Хокинг полагал, что принцип неопределенности “размажет” предсказанные общей теорией относительности сингулярности, подобно тому как размазано положение электрона. Не происходит коллапса атома – и аналогично, подозревал Хокинг, не было и сингулярности в начале вселенной, нет ее и внутри черной дыры. Да, космос был тогда сжат до предела, и все же не в точку бесконечной плотности.

Общая теория относительности предсказывала, что внутри черной дыры и в момент Большого взрыва искривление пространства-времени достигает бесконечности. Если этого не происходит, то Хокингу оставалось вычислить, “какую форму пространство и время принимают вместо точки бесконечной кривизны”.

Если эта подглавка покажется вам чересчур сложной, можете ее смело пропустить. Чтобы постичь теорию Хокинга, нет надобности вникать в каждое слово, но вам будет интереснее, если вы в этом разберетесь. Разумеется, уравнения, к которым прибегал Хокинг, гораздо сложнее этого упрощенного рассказа, и, наверное, чтобы вполне понять теорию Хокинга, надо было бы вникнуть еще и в его математику.

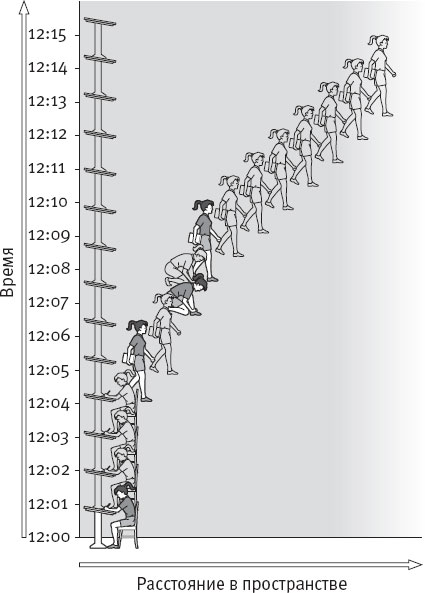
Рис. 10.1. Кейтлин в пространстве-времени.

Теория относительности соединяет пространство и время. Получается четырехмерное пространство-время: три измерения пространства и одно – времени. Посмотрите, как выглядит диаграмма пространства-времени. Рисунок 10.1 я однажды набросала, изобразив свою дочку Кейтлин по пути из школьного класса в столовую. Вертикальная линия слева отражает ход времени. Любая точка графика отражает позицию в пространстве и момент времени. Присмотритесь, как это устроено.

Сначала, в 12.00, Кейтлин изображена в классе за партой. Она сидит спокойно, перемещаясь только во времени, но не в пространстве. На рисунке разворачивается короткая цепочка Кейтлин, перемещающихся во времени. В 12.05 звенит звонок. Кейтлин направляется в столовую. Ее парта продолжает перемещаться во времени, оставаясь неподвижной в пространстве, Кейтлин же теперь двигается и во времени, и в пространстве. В 12.07 она останавливается завязать шнурок. Минуту она движется во времени, но не в пространстве. В 12.08 она возобновляет движение по направлению к столовой и теперь шагает чуть быстрее, а то, пока дойдет, все расхватают. В 12.15 она входит в столовую. Мы проследили “мировую линию” Кейтлин, как выразился бы физик.

Эта диаграмма пространства-времени – всего лишь набросок. Составляя настоящую диаграмму пространства-времени, физики используют специальную единицу, объединяющую время и пространство, например, метр времени. (Метр времени – это очень малая доля секунды, меньше миллиардной доли, – время, за которое фотон, движущийся со скоростью света, проходит один метр.) На такой диаграмме объект, проходящий четыре метра пространства за четыре метра времени, будет представлен линией, проходящей под углом в 45 градусов к осям. Это график движения со скоростью света – например, фотона (рис. 10.2).

Если за четыре метра времени объект проходит три метра пространства, его скорость составляет три четверти скорости света (рис. 10.3а). И наоборот, четыре метра пространства за три метра времени означало бы превышение скорости света, что недопустимо.

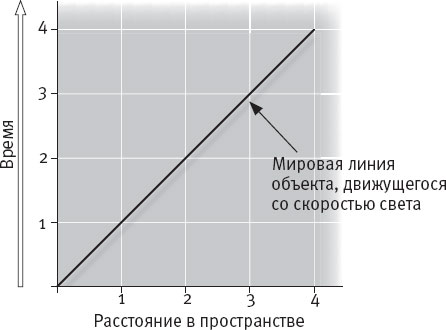
Рис. 10.2. На графике пространства-времени метр служит мерой и времени, и пространства. Если объект проходит четыре метра в пространстве и четыре метра во времени, его “мировая линия” идет под углом 45 градусов к осям пространства и времени. Такова мировая линия фотона и любого объекта, движущегося со скоростью света.

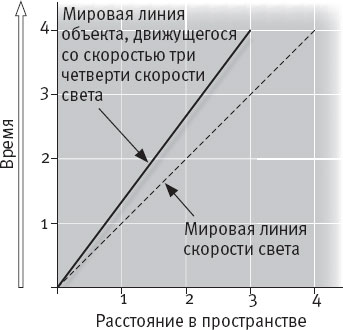
Рис. 10.3a. На графике пространства-времени представлена мировая линия объекта, проходящего три метра в пространстве и четыре метра во времени, то есть движущегося со скоростью три четверти скорости света.

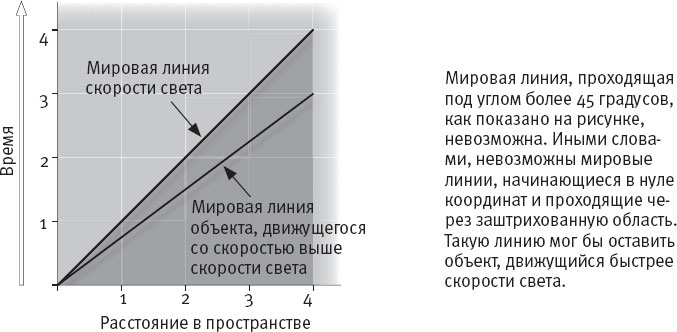
Рис. 10.3b. Мировая линия объекта, проходящего четыре метра в пространстве и три во времени. Если расстояние, преодоленное в пространстве, превышает расстояние во времени, то объект движется со скоростью выше скорости света (не допускается).

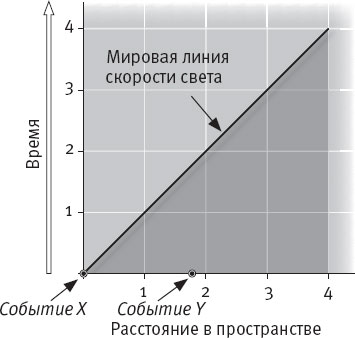
Рис. 10.4. График пространства-времени представляет два одновременных события (X и Y), которые происходят на некотором расстоянии друг от друга в пространстве. В тот момент, когда эти события происходят, они не знают друг о друге, потому что узнать друг о друге в тот же момент они могли бы, только если бы информация распространялась быстрее, чем со скоростью света, то есть ее мировая линия проходила бы под углом больше 45 градусов, а это в нашей вселенной не допускается.

На следующем рисунке (рис. 10.4) изображены два одновременных события. В тот момент, когда эти события происходят, они не знают друг о друге, поскольку для того, чтобы они друг о друге узнали, потребовалась бы мировая линия информации, проходящая под прямым углом к оси времени, иными словами, информация должна была бы распространяться со скоростью, превышающей скорость света. Однако ничто не может развивать скорость, превышающую скорость света, и даже мировая линия света проходит под углом 45 градусов к осям.

Теперь поговорим о “длине” мировой линии. Как выразить эту длину – “протяженность”, учитывающую все четыре измерения?

Рассмотрим мировую линию объекта, который движется намного быстрее Кейтлин. Объект на рисунке 10.5 проходит четыре метра пространства и пять метров времени, то есть его скорость составляет четыре пятых скорости света. Расстояние, которое этот объект проходит в пространстве, обозначено на рисунке пунктирной линией, которую мы будем рассматривать как одну из сторон треугольника (сторона А). Путь во времени на том же рисунке обозначен линией, которую мы примем за другую сторону треугольника (сторона B). Так мы получили два катета прямоугольного треугольника, а гипотенуза (сторона С) и есть мировая линия движущегося объекта.

Все мы со школьных лет помним, что квадрат гипотенузы равен сумме квадратов катетов. Квадрат 4 (сторона А) – 16, квадрат 5 (сторона B) – 25. Сумма 16 + 25 равна 41. Таким образом, длина стороны С, то есть гипотенузы, равна квадратному корню из 41.

Не пытайтесь вычислить квадратный корень из 41. Это уже другая проблема – если бы мы продолжали и тут применять школьную геометрию, нам пришлось бы вычислять иррациональный корень из 41. Но в пространстве-времени все устроено иначе, и квадрат гипотенузы (стороны С) не равен сумме квадратов катетов: он равен их разности. Рассматриваемый объект проходит четыре метра в пространстве (сторона А треугольника) и пять метров во времени (сторона B). Квадрат 4–16, квадрат 5–25. Разность 25–16 равна 9. Квадратный корень из 9–3. Итак, третья сторона треугольника, сторона С, мировая линия движущегося объекта, имеет в пространстве-времени длину три метра.

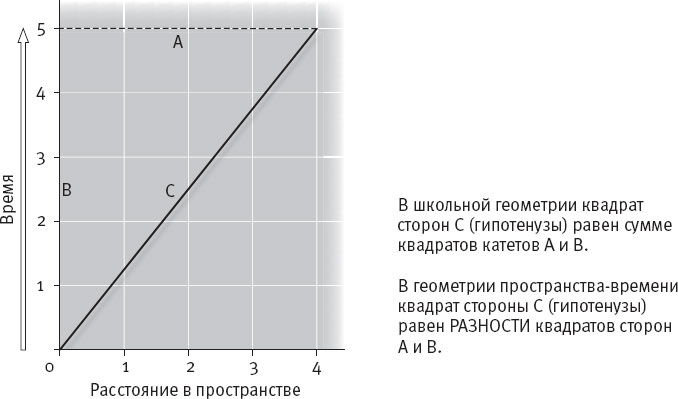
Рис. 10.5. В прямоугольном треугольнике расстояние в пространстве обозначено катетом А, расстояние во времени катетом В, а мировая линия в пространстве-времени – гипотенузой С.

Теперь представим себе, что наш объект – человек и на руке у него часы. Часы покажут эту длину (три метра времени) как “время”. На рисунке 10.6 Лорен остается неподвижна в пространстве, пока ее часы отсчитывают пять часов. Ее брат-близнец Тим движется со скоростью четыре пятых скорости света, и для него, пока у Лорен проходит пять часов, проходит всего три часа. Тим разворачивается и возвращается, вновь отсчитав три часа, пока Лорен отсчитывает пять. Теперь, когда они встретятся, Тим окажется чуть-чуть моложе своей сестры-близнеца. Это один из замечательных парадоксов вселенной, которым научил нас Эйнштейн.

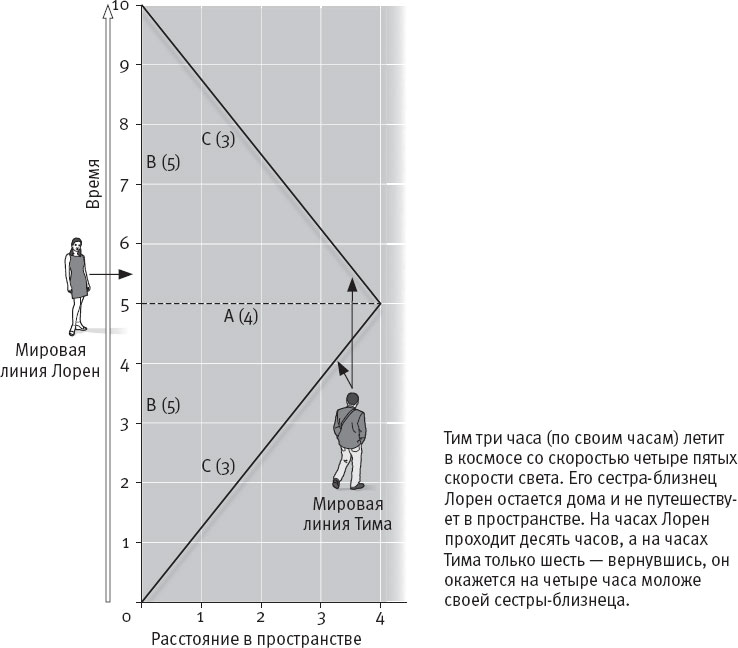
Тим три часа (по своим часам) летит в космосе со скоростью четыре пятых скорости света. Его сестра-близнец Лорен остается дома и не путешествует в пространстве. На часах Лорен проходит десять часов, а на часах Тима только шесть – вернувшись, он окажется на четыре часа моложе своей сестры-близнеца.

Теперь рассмотрим пространственно-временные диаграммы и мировые линии объектов поменьше – элементарных частиц.

Мы уже обсудили “размазанную” позицию электронов в атомной модели. Эта позиция “размазана”, потому что невозможно одновременно с большой точностью измерить позицию и движение любого электрона. Ричард Фейнман нашел способ решить эту проблему – теперь мы называем этот способ “суммой историй”.

Предположим, мы решили рассмотреть все маршруты, по которым Красная Шапочка добирается из дома до бабушки. Не только самый быстрый путь, по прямой, и не только самый безопасный, в обход волчьего леса, но вообще все мыслимые маршруты. Их миллиарды и миллиарды. В итоге получится гигантская размытая картинка, на которой будут представлены все линии и кривые, как будто Красная Шапочка движется одновременно по всем направлениям. Тем не менее среди этих маршрутов есть некоторые наиболее вероятные. Изучая вероятность маршрутов Красной Шапочки, мы придем к выводу, что она вряд ли по пути к бабушке заглянула на Венеру, то есть вероятность этого крайне мала, но все же, по мнению Фейнмана, и такой вариант исключать нельзя. Крайне низкая вероятность – это не ноль.

По такому же принципу “суммы историй” физики рисуют в пространстве-времени все возможные маршруты конкретной частицы, все ее вероятные “истории”. Затем вычисляется вероятность прохождения частицы через конкретный пункт – так мы вычисляли вероятность визита Красной Шапочки на Венеру. (Только не думайте, будто частицы выбирают свой путь. Это уж значило бы чересчур далеко заходить с аналогией.)

Хокинг нашел методу суммы историй другое применение: он предложил рассмотреть все истории, какие могли быть у вселенной (вернее, те из них, которые представляются наиболее вероятными).

Прежде чем идти дальше, сделаем одну оговорку: хотя теория относительности приучила нас к понятию пространства-времени с четырьмя измерениями – три пространства, одно времени, – между временем и пространством имеются все же физические различия. Одним из этих различий объясняется особенность измерения расстояния между двумя точками пространства-времени – гипотенузы рассмотренного выше треугольника.

Рисунок 10.7а представляет два автономных события на графике пространства-времени. Эти события соединены мировой линией, которая отклоняется от оси времени более чем на 45 градусов. Эти две точки не могут обмениваться информацией, поскольку информация не распространяется со скоростью, превышающей скорость света. В таком случае – если расстояние между двумя событиями в пространстве превышает расстояние между ними во времени – квадрат гипотенузы (сторона С) является положительным числом. На языке физики: квадрат “четырехмерного расстояния” между событиями X и Y – положительное число.

На рисунке 10.7b также изображены два события. Расстояние во времени между ними больше расстояния в пространстве. Соединяющая их мировая линия отклоняется от оси времени менее чем на 45 градусов. Информация успеет попасть из точки X в точку Y, путешествуя со скоростью ниже скорости света. То есть в физике квадрат четырехмерного расстояния между событиями X и Y – отрицательное число.

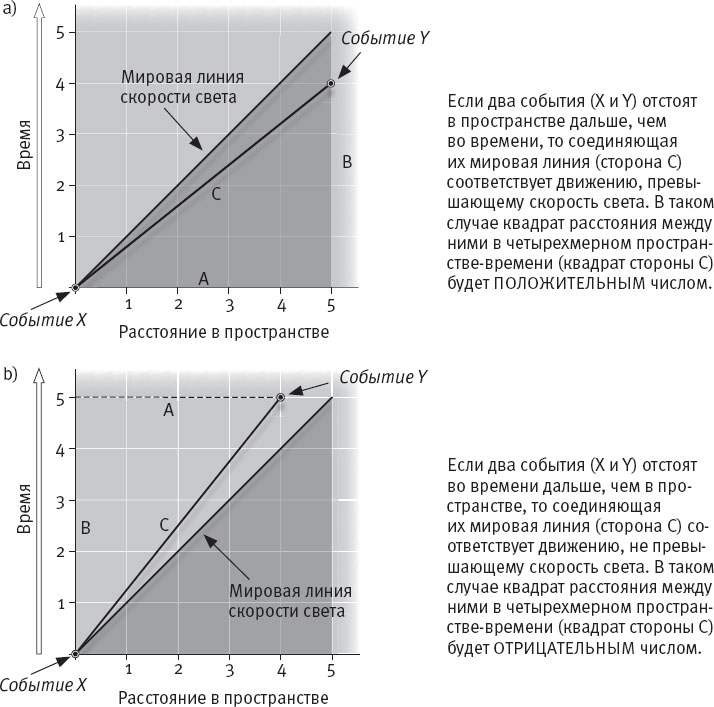
Рис. 10.7. Разница между пространством и временем.

Вы еще не заблудились? Последние два абзаца были трудноваты. И если вы читали внимательно, сейчас, вероятно, в вашем мозгу вспыхнул тревожный сигнал. Квадрат числа не бывает отрицательным! В нашей математике такого просто не может быть. Если квадрат окажется отрицательным, то как извлечь квадратный корень? Сколько будет – квадратный корень из –9? В нашей математике квадрат любого числа, и положительного, и отрицательного, – всегда положительное число. Три в квадрате – девять и минус три в квадрате – тоже девять. Минус девять не получится, как ни крути. Квадрат не бывает отрицательным, и точка.

Стивен Хокинг и другие физики сумели обойти это противоречие. Допустим, что все же существуют числа, которые, будучи умножены на самих себя, дают отрицательное произведение. Допустим – и посмотрим, что произойдет. Скажем, некое воображаемое число, умноженное на самое себя, дает минус единицу. Вычислим истории частиц и истории вселенной, используя эти воображаемые числа. Будем вести расчеты в “мнимом”, а не в “реальном” времени. Время, которое нужно, чтобы добраться из пункта X до пункта Y на рисунке 10.7b, – мнимое время. Квадратный корень из минус девяти – мнимая тройка.

Пусть эти числа послужат для нас математическим приемом (даже фокусом, если угодно) в расчетах, которые иначе не имели бы смысла. “Мнимое время” позволяет физикам точнее рассчитывать гравитацию на атомном уровне и по-новому взглянуть на раннюю историю вселенной.

Если вернуться вспять к началу вселенной, по мере того как пространство будет становиться все более плотным, все меньше будет вариантов местонахождения частицы в данный конкретный момент. А значит, как гласит принцип неопределенности, чем точнее мы будем знать позицию частицы, тем менее точно сможем измерять ее движение.

Для начала рассмотрим частицу света, фотон, при нормальных условиях. Фотоны движутся со скоростью 300 000 километров в секунду – это и есть скорость света. Но теперь я вынуждена сказать вам, что это может быть и не так (вы уже, наверное, привыкли к подобным парадоксам). Мы убедились, что вероятность найти электрон размазана в определенной области вокруг атомного ядра – одни расстояния от ядра представляются более вероятными, чем другие, но все размазано и нечетко. Принцип неопределенности не позволяет нам точно установить одновременно и положение, и движение электронов, и этот же принцип действует по отношению к фотонам.

Ричард Фейнман и другие физики пришли к выводу, что вероятность движения фотона со скоростью 300 000 км/с распределяется по некоторой “области” возле этой скорости. Иными словами, скорость фотона колеблется около той величины, которую мы называем скоростью света. На большом расстоянии вероятности уравновешиваются и средняя скорость фотона действительно равна 300 000 км/с. Но на малом расстоянии, на квантовом уровне, существенно, если фотон движется чуть быстрее или чуть медленнее. Напрямую эти флуктуации наблюдать невозможно, однако путь электронов на диаграмме пространства-времени будет выглядеть не как прямая линия под углом в 45 градусов к осям, а несколько размыто.

В ранний период существования вселенной эта линия становится очень размытой. Принцип неопределенности гласит: чем точнее мы знаем положение фотона, тем менее точно знаем его движение. Если в самом начале вещество вселенной было “упаковано” с почти бесконечной плотностью (пусть не сингулярность, но близко к тому), появляется возможность с большой точностью судить о положении частиц, в том числе фотонов, а раз появляется точное знание об их положении, во много раз вырастает неопределенность их движения. Чем ближе к бесконечной плотности, тем ближе к бесконечности число вероятностей различных скоростей фотона. Что теперь произойдет с нашим графиком пространства-времени? Посмотрите на рисунок 10.8. Мировая линия фотона, в нормальных обстоятельствах приближавшаяся к прямой под углом в 45 градусов к осям, теперь отчаянно колеблется, сплошные подъемы и спады.

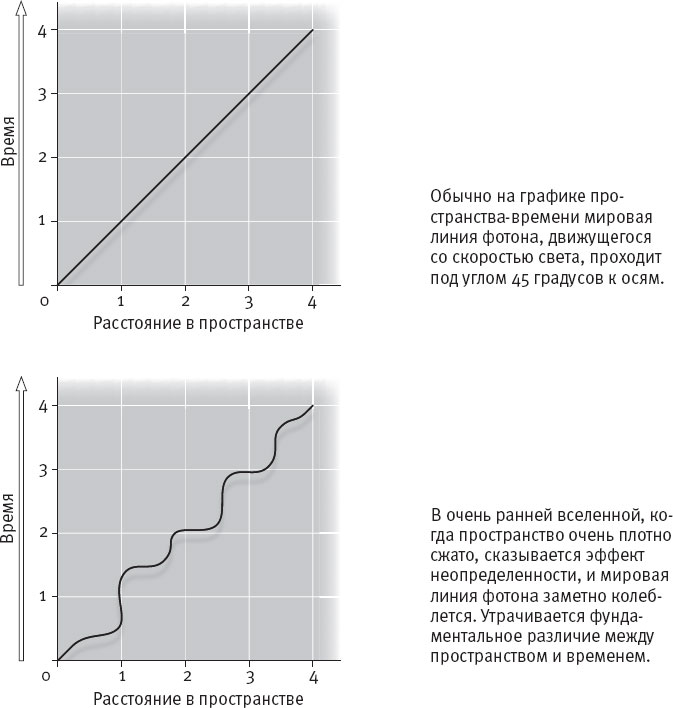
Рис. 10.8. Действие принципа неопределенности в ранней вселенной.

Есть и другой подход к вопросу о том, что вызывает эти “колебания”, причем подход этот тесно связан с основными концепциями, которые мы рассматриваем в нашей книге. Возвращаясь вспять к самому началу вселенной, мы должны съежиться до бесконечно малых размеров и сможем увидеть то, что происходит на уровне бесконечно малых. Представьте себе это так: вот вы смотрите на эту страницу, и она кажется вам вполне гладкой. Можно свернуть уголок, но и в свернутом виде страница останется гладкой. Так и окружающее нас пространство-время кажется гладким, несмотря на кривизну. Однако положите эту же страницу под микроскоп, и вы увидите неровности, даже рытвины. И, рассматривая пространство-время на уровне бесконечно малых, в миллиарды миллиардов раз меньше размеров атома, мы обнаружим серьезные отклонения в геометрии пространства-времени (рис. 10.9). К этому вопросу мы еще вернемся в главе 12 и тогда познакомимся с одним из следствий – с “кротовыми норами”. Пока же важно, что такие мощные отклонения происходят на раннем этапе существования вселенной, когда все вещество стиснуто до предела.

Как понять этот неистовый хаос? Обратимся вновь к принципу неопределенности. В главе 6 мы видели, что принцип неопределенности также применяется к полям: электромагнитное или гравитационное поле не может одновременно обладать и определенным значением, и определенной скоростью перемен, а поскольку ноль – точная мера, поле такую меру иметь не может. Однако в пустом пространстве все поля сводятся к нулю. А раз ноль невозможен, невозможно и пустое пространство. Что же мы получаем вместо пустого пространства? Постоянное колебание значения всех полей, флуктуации по ту и по другую сторону от абсолютного нуля – в среднем будет ноль, но в реальности нуля не будет. Флуктуацию можно представить в виде парных частиц излучения Хокинга. Чем сильнее и чаще меняется кривая пространства-времени, тем больше появляется таких пар. Вот почему они в огромном количестве ожидаются на горизонте событий черной дыры.

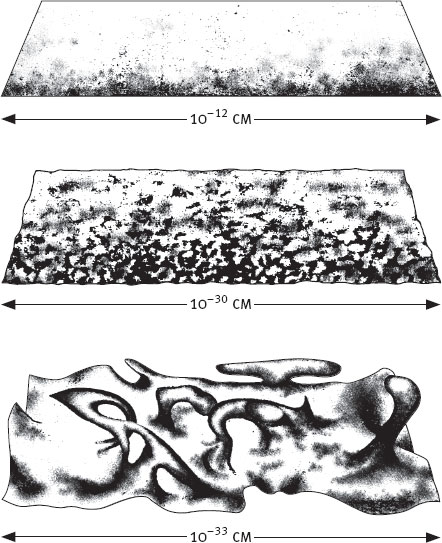
Рис. 10.9. Квантовый вакуум, как представлял его себе Джон Уилер в 1957 году, становится все более хаотичным по мере того, как мы рассматриваем все меньшие участки пространства. В масштабе атомного ядра (верх) пространство все еще выглядит вполне гладким. Посмотрев пристальнее (середина), мы заметим некоторую шероховатость, а в масштабе в 1000 раз меньшем (низ) начнутся сильные флуктуации.

В самом начале вселенной кривая пространства-времени чрезвычайно велика и очень быстро меняется. Квантовые флуктуации во всех полях, включая гравитационное, очень сильны. Подобные возмущения в гравитационном поле означают не менее сильные колебания кривой пространства-времени. Возникают все время изменяющиеся складки, морщинки, завихрения. В подобном хаосе начинает чудить и мировая линия фотона. (Посмотрите снова на рис. 10.8 и 10.9.)

Какое бы из объяснений мы ни выбрали, суть в том, что стирается различие между вектором времени и векторами пространства. Время становится похожим на пространство, и мы лишаемся привычной картины, в которой вектор времени всегда лежит внутри 45-градусного угла, а направления пространства всегда вне этого угла.

Хокинг подытоживает: “В начале вселенной, когда пространство было тесно сжато, принцип неопределенности мог изменить фундаментальное отличие пространства от времени”. В этой ситуации уже неверно утверждение: “Если события отстоят друг от друга во времени больше, чем в пространстве, квадрат расстояния между ними в пространстве-времени (квадрат гипотенузы нашего прямоугольного треугольника) неизбежно окажется отрицательным числом”. “В определенных обстоятельствах квадрат расстояния может оказаться положительным числом. В таком случае уничтожается последнее различие между временем и пространством – можно сказать, время полностью становится пространственным, – и приходится говорить уже не о пространстве-времени, а о четырехмерном пространстве”.

Как это выглядит? И каким образом непонятное четырехмерное пространство плавно переходит в знакомое нам пространство-время, где время течет, как это свойственно времени? Концепция мнимого времени позволяет нам вообразить четырехмерное пространство, в котором время в привычном нам виде не существует – оно свернулось и образовало сплошную поверхность, без краев и границ. Но если вы думаете, что сможете представить себе эту картину в четырехмерном пространстве, то либо обманываете самих себя, либо ваш мозг поднялся на новую ступень эволюции. Большинство людей вынуждены все же ограничиться меньшим количеством измерений. Когда измерений меньше, еще можно представить себе отсутствие границ и краев: поверхность мяча или Земли.

В первой модели, предложенной Фридманом, размеры вселенной были конечными – и все же вселенная не имела границ. Не было края, за которым она кончалась и начиналось пустое пространство. Вселенная – как мяч: размеры ограниченны, но поверхность сплошная, без краев. Хокинг предполагал, что такой – конечной и вместе с тем безграничной – вселенная может быть и в пространстве-времени. Возможно, и у времени нет начала и конца. Все движется по кругу, образуя замкнутую поверхность, подобную поверхности Земли.

Но что же нам с этим делать? Поверхность Земли мы себе хорошо представляем и понимаем, в каком смысле она и конечна, и безгранична, однако вселенная, конечная и безграничная в пространстве-времени? На что это похоже? От оболочки шара трудно перейти к осмысленной концепции четырехмерной вселенной. Пытаешься – и чувствуешь себя слепцом. Нащупываешь путь и сбиваешься в темноте. Давайте лучше поищем какие-нибудь вехи.

Во-первых, можно указать, на что это непохоже. Не будет никаких “граничных условий”, ведь не будет начала, границы во времени. Вся эта штука попросту свернется и замкнется на саму себя. Хокинг формулирует кратко: граничные условия вселенной – отсутствие граничных условий. Нет начала вселенной и нет конца – нигде. Так что не стоит и спрашивать: а что, мол, было до того? Все равно что интересоваться: а что находится к югу от Южного полюса? На Южном полюсе не может быть указателя с надписью “Юг”. Стрелка с надписью “Прошлое” теряет смысл, когда время становится “пространственным”.

Если на временной оси нет никакого “до” вселенной и “после” вселенной, может ли там найтись “другое место”, что-то вне вселенной – в каком-либо измерении пространства? Модель Хокинга такой возможности не исключает. Может ли быть некое “снаружи” при отсутствии границ? Пока речь шла о мяче, вероятность наружных объектов не исключалась. Где-то в том направлении, куда мог бы посмотреть сидящий на шаре муравей из главы 6, – но он, как вы помните, выглянуть за пределы шара не может. Это измерение не существует для муравья, что, однако, вовсе не означает, будто этого измерения вовсе нет. Идея “других мест” в пространстве, но не “прежде” или “потом” во вселенной, вполне соответствует концепции времени как недолговечной мутации – на самом деле это четвертое измерение пространства.

Все это кажется слишком заумным, а потому едва ли правдоподобным, но рассмотрим вопрос более прямо и просто. Повторим еще раз: как могла бы выглядеть вселенная, конечная и в то же время безграничная в пространстве и времени? Требуются страшно сложные подсчеты, но в результате выходит, что эта вселенная, скорее всего, была бы похожа на ту, в которой мы живем.

Хокинг описывал это так: “Предполагается, что вселенная началась из достаточно “гладкого”, единообразного состояния. Она прошла через период расширения по экспоненте, “инфляции”, когда ее размеры многократно увеличились, но плотность оставалась прежней. Затем вселенная разогрелась и расширилась до современного своего состояния, остывая по мере того, как расширялась. В крупном масштабе она была однообразной, одинаковой по всем направлениям, но на местном уровне имелись отклонения, превратившиеся затем в звезды и планеты”.

В реальном времени – там, где мы живем, – все будет выглядеть так, словно в начале вселенной и внутри черных дыр имеются сингулярности.

Хокинг и Джим Хартл представили эту модель вселенной научному сообществу в 1983 году. Хокинг особо подчеркивал, что это всего лишь гипотеза. Он не вывел такие граничные условия из какого-либо принципа. Просто ему понравилась такая модель. Он подумал, “что это и есть настоящая наука, ведь, по сути дела, сим утверждается, что научные законы действуют повсюду”. Нет сингулярностей, в которых нарушались бы законы. Такая вселенная самодостаточна. Нужно ли объяснять, как она была создана? Обязательно ли вообще это слово – “создана” или “возникла”? “Она бы просто БЫЛА”, – пишет Хокинг.

Напрашивается несколько чисто философских вопросов. Сам Хокинг сформулировал основной: “Если у вселенной нет границ и она самодостаточна… то у Бога не имелось возможности выбирать, с чего начинается вселенная”.

Хокинг не утверждает, что отсутствие граничных условий исключает существование Бога, – он лишь отнимает у Бога выбор, как положить начало вселенной. Не все ученые согласились с ним. Они сочли, что отсутствие граничных условий не слишком-то ограничивает Бога. Даже если у Бога будет отнят выбор, мы зададимся вопросом: а кто решил, что у Бога не должно быть выбора? Этих взглядов придерживался и Дон Пейдж, писавший рецензию на “Краткую историю времени” для журнала Nature. Пейдж, как мы помним, в конце 1970-х был аспирантом и помощником Хокинга. Затем он переехал в Канаду и сделался профессором в Альбертском университете. Их дружба с Хокингом продолжалась, они вместе написали ряд научных работ, и Хокинг знал, что Пейдж постарается найти аргументы и доказать, что и отсутствие граничных условий не отменяет необходимости Творца. Пейдж с этой задачей справился.

На вопрос Хокинга “Так где же место Творцу?” Пейдж ответил, что в иудео-христианской концепции мира “Бог создает и поддерживает вселенную целиком, а не только ее начало. Даже если у вселенной нет начала, это не значит, что она не сотворена, – ведь если художник вместо прямой линии с началом и концом нарисует замкнутый круг, это все равно будет нарисованная фигура, а не возникшая сама собой”. Бог, существующий вне нашей вселенной и нашего времени, не нуждался бы в “начале”, чтобы сотворить мир, – это с нашей точки зрения в “реальном” времени мир все равно выглядел бы (или мог бы выглядеть) так, словно у него было начало.

В “Краткой истории времени” Хокинг высказал предположение, что место для Творца все же найдется. “В самом ли деле единая теория настолько убедительна, что она сама себя порождает?” Если нет, “то что же вдыхает пламень в уравнения и создает вселенную, которую эти уравнения описывают?”. В книге “Краткая история времени: путеводитель для читателя” Хокинг напишет, что если гипотеза об отсутствии граничных условий верна, значит, он сумел понять, как началась вселенная. “Но я все равно не знаю, почему она началась”. И он хотел бы это выяснить, если получится.

Вот почему нужно сделать существенную оговорку: хотя физики-теоретики отваживаются на самые дерзкие, проникающие в начало и суть вселенной вопросы и хотя они обрушивают на нас поражающие ум гипотезы и теории, они не претендуют на “окончательный ответ” – даже если подзаголовок книги, соавтором которой был Хокинг, предполагает, что они пытаются этот ответ получить. Научный прогресс в том и заключается, что предлагаются какие-то “ответы”, а затем эти “ответы” анализируются и опровергаются. Отважные и наделенные живым воображением ученые спускают на воду очередной игрушечный кораблик и почему-то изо всех сил стараются потопить свою игрушку.

Наглядный пример тому – работа Хокинга. Сначала он доказал, что вселенная возникла из сингулярности. Потом выступил с гипотезой об отсутствии граничных условий и доказал, что сингулярности могло и не быть. Он сообщил нам, что черные дыры не могут уменьшиться в размере, а потом обнаружил, что как раз могут. Исследуя Большой взрыв, он вроде бы совпал с библейской точкой зрения на Творение, но гипотеза об отсутствии граничных условий лишила Творца работы – или, по крайней мере, изменила наши представления об этой работе. В “Краткой истории времени” Хокинг вновь вернулся к необходимости Творца и заявил, что “высшим торжеством для человеческого разума” будет “понять замысел Бога”. Хокинг открыт новым идеям и сам подбрасывает провокационные гипотезы – так устроены лучшие умы человечества. Он приходит к четко сформулированному, хорошо обоснованному выводу и тут же беспощадно перепроверяет и опровергает этот вывод. Он всегда готов признать неправильность или неполноту своих взглядов. Так и развивается его наука – вероятно, так развивается всякая настоящая наука, – и это одна из причин, почему в основе физики столько парадоксов.

Пока Хокинг проходит свой путь, его разбирают на цитаты в пользу противоборствующих мировоззрений. Его цитировали – и на все лады искажали – и те, кто верит в Бога, и кто в Него не верит. В обоих лагерях одни его держат за героя, другие – за злодея. И те, кто опирается на мнение Хокинга или на мнения других ученых, пытаясь подкрепить ими свою веру или неверие, становятся на скользкий коврик, который в любой момент грозит выскочить у них из-под ног.

Однако хотя гипотеза об отсутствии границ может показаться радикальным пересмотром прежних взглядов, сам Хокинг так не считает. Он говорит, что главным результатом исследования сингулярностей стало понимание: гравитационное поле возрастает настолько, что проявляется и на квантовом уровне. Когда же мы обращаем внимание на события квантового уровня, мы видим, что вселенная может быть конечна в мнимом времени, но при этом не иметь ни границ, ни черных дыр.

В 1983 году, в том самом, когда Хокинг и Джим Хартл опубликовали гипотезу об отсутствии граничных условий, Андрей Линде выступил с новым предложением, позволявшим устранить все еще остававшиеся в теории инфляции проблемы. Первым человеком на Западе, с кем Андрей поделился теорией “хаотичной инфляции”, стал Хокинг. Хокинг пришел в восторг.

И “старая”, и “новая” теории инфляции предполагали, что инфляция – лишь краткий период в истории ранней вселенной, что до начала инфляции вселенная находилась в состоянии термального равновесия (то есть температура повсюду была одинаковой), вселенная была более-менее однородной и при этом достаточно большой, чтобы сохраниться до инфляции. Линде отказался от этих предпосылок и создал другой сценарий – хаотической инфляции, которая не предусматривала термального равновесия. В таком случае инфляция могла начаться раньше, ближе к моменту Большого взрыва.

До периода инфляции вселенная, возможно, пребывала в состоянии хаоса. Требовалось лишь, чтобы в крошечных областях этого хаоса могла начаться инфляция. Эти области в процессе инфляции становились более гладкими, изотропными (то есть однородными по всем направлениям) – подобно тому, как сморщенный шарик, раздуваясь, становится гладким и одинаковым по всем направлениям. Насколько нам известно, это происходило только с небольшой частью хаоса, хотя могло быть и не так. Во всяком случае, “наш” шарик, надуваясь, растолкал другие надувавшиеся шарики так далеко, что мы не сумеем их увидеть. Может быть, в других частях вселенной все еще царит хаос. А может быть, все и повсюду выровнялось.

В сценарии хаотической инфляции нет места фазовому переходу или сверхохлаждению. Зато имеется поле, которое в одних областях вселенной достигает высоких значений, а в других остается низким. “Счастливое упущение Творца”, как поэтически выразился Линде. По мнению Линде, в областях с высоким значением поля энергия окажется настолько велика, что вызовет центробежный гравитационный эффект и инфляционное расширение этих областей, а в других областях, где поле не настолько сильно, этого не случится. Области, где произойдет инфляция, превратятся в огромные гомогенные острова внутри первозданного хаоса, и каждый остров будет намного больше видимой вселенной. В этих областях энергия поля будет убывать медленно, и в некоторых из них скорость расширения постепенно станет такой, какую мы наблюдаем теперь. При достаточном количестве подобных областей высока вероятность, что найдется хоть одна область, где возникнет вселенная, которая нам известна, где константы, они же произвольные элементы физических теорий, окажутся как раз такими, чтобы в итоге могли появиться вы и я. Возможно, такая вселенная всего одна и это – наш мир.

Хороший конец истории… вот только это вовсе не конец. Теория хаотической инфляции предсказывала также “вторую стадию инфляции”, которая наступит значительно позднее, – ускоренное расширение вселенной. И оно может произойти прямо в наши дни. В начале 1980-х подобное предположение даже Андрею Линде и Стивену Хокингу казалось фантастическим. Но к концу столетия, как мы увидим, оно уже не воспринималось как художественный вымысел.

Хотя ученые еще спорили о том, как именно происходила инфляция, в целом эта теория в начале 1980-х утвердилась, и самое интересное: при всех разногласиях космофизики сходились на том, что вся видимая и известная нам вселенная могла начаться с куда меньшего отклонения в массе и энергии, чем это раньше казалось возможным. В “Книге вселенных” Джон Барроу писал: “Теория инфляции не устранила нерегулярности, а вымела их за пределы ныне видимого горизонта вселенной. Они остаются где-то там, вдалеке, но видимой вселенной присущи гладкость и изотропия крошечной области космоса, которая пережила инфляцию”.

Разумеется, наша вселенная не полностью однородна. В ней есть солнечные системы, галактики и кластеры галактик. Тот кусочек, который расширился и превратился в нашу вселенную, выходит, не был идеально гладким, как наш воображаемый шарик. При растяжении не удалось избежать небольших отклонений, и из этих семян выросла вся поразительная структура – нынешние весьма заметные отклонения в плотности.

Уже на конференции, созванной Хокингом и Гиббонсом в Кембридже в 1982 году, участники пришли к выводу, что инфляция подразумевает определенную схему этих отклонений. Значит, в космическом микроволновом фоновом излучении тоже должны были обнаружиться распознаваемые паттерны. В ту пору наблюдения не могли различить эти паттерны отклонений. И все же, хотя никто не может заглянуть в события начала вселенной, в этих спорах вокруг инфляции появилась надежда, что однажды удастся все же добыть убедительное доказательство либо в пользу этой гипотезы, либо в опровержение.