Книга: 0,05. Доказательная медицина от магии до поисков бессмертия
Назад: Глава 6 Числа
Дальше: Часть третья Герои и мерзавцы
Глава 7
Статистика и рандомизация
Часовщик играет в кости
К началу XIX века физики и астрономы стали уделять внимание факту, которому раньше не придавали большого значения: одни и те же измерения, например замеры координат небесных тел, никогда не давали в точности тот же результат. Сначала эти расхождения игнорировали, используя одно произвольно выбранное значение. Но постепенно стало понятно, что хотя приборы становятся точнее и разброс полученных значений уменьшается, он никогда не исчезает полностью. Примерно одновременно математики Карл Фридрих Гаусс в Германии и Пьер-Симон Лаплас во Франции попытались сформулировать, как, опираясь на результаты серии измерений, вычислить то одно истинное значение, которое скрывается за ними.
Гаусс и Лаплас обнаружили, что при достаточно большом количестве измерений их результаты распределяются в соответствии с тем, что сейчас мы называем нормальным (или Гауссовым) распределением. Если построить график, разместив по оси x значения измерений, а количество измерений, при которых получено такое значение, – по оси y, мы получим кривую, похожую на колокол: близкие к среднему значения будут встречаться чаще всего, а чем дальше значение от среднего, тем реже оно будет встречаться.
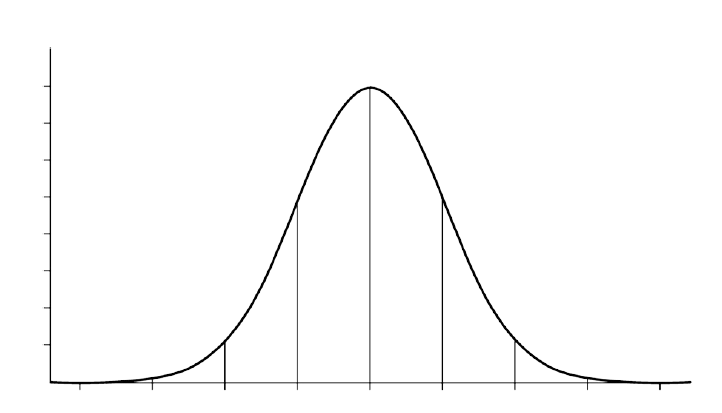
Нормальное распределение характерно для случайных процессов с результатом, складывающимся под влиянием многих независимых воздействий, каждое из которых вносит свой небольшой вклад. Нормальное распределение часто встречается в природе. Так распределены в популяции размеры живых организмов, отдельных органов, тканей, конечностей, некоторые психические и физиологические параметры, такие как коэффициент интеллекта.
Если у вас есть немного свободного времени и пять игральных кубиков, вы можете провести небольшой эксперимент – он поможет понять, почему и как это происходит. Возьмите листок бумаги и начертите оси координат. Ось х разметьте от пяти до тридцати. После каждого броска суммируйте значения выпавших сторон и добавляйте по одному делению по оси y над тем значением суммы, которое выпало. Поскольку средние значения сумм образуются бóльшим количеством комбинаций, а значит чаще, чем очень маленькие или очень большие, то средняя часть графика начнет заполняться намного быстрее.
Вам может понадобиться немало бросков перед тем, как вы увидите характерную кривую нормального распределения. Если у вас не так много времени, воспользуйтесь автоматическим сервисом, который делает то же самое – вы найдете его на сайте Academo.org. Отметьте галочкой опцию Roll automatically и наблюдайте, как по мере стремительного увеличения количества бросков ваш график все больше становится похож на колокол.
Гаусс первым использовал при расчете орбиты небесного тела представление о нормальном распределении результатов наблюдений. Рассчитав таким образом вероятности реального положения орбиты астероида Цереры, он смог достаточно точно предсказать движение небесного тела, исходя из очень небольшого количества данных. Так статистика и теория вероятностей стали постепенно вытеснять царивший в экспериментальной науке детерминизм.
Детерминизм исходит из того, что все события полностью предопределены вызвавшими их причинами. Возможно, так оно и есть, но на практике мы не можем предсказать исход многих процессов в силу их высокой сложности, то есть большого количества факторов, каждый из которых вносит свой вклад.
Теоретически мы можем заранее просчитать результат броска игральных кубиков, если построим точную модель траектории их движения с учетом скоростей, угловых скоростей, отклонения осей вращения, высоты броска, сопротивления воздуха и свойств поверхности, на которую они упадут. Но зачастую у нас нет возможности получить всю информацию, необходимую для построения детерминистической модели. Более того, минимальные изменения начальных данных (угла, силы, высоты) приведут к принципиальному изменению результата броска. Поэтому на практике такой подход неприменим. Зато мы можем оперировать вероятностями, которые определяем, исходя из того, как кубики вели себя в прошлом, и с их помощью предсказывать шансы на те или иные результаты в будущем.
Еще в большей степени это справедливо для биологических процессов, к которым относится и все происходящее в человеческом теле в норме и в болезни. Тело взрослого человека намного сложнее, чем бросок игральных кубиков. Оно состоит из сорока триллионов клеток, созданных наследственной программой, состоящей, в свою очередь, из трех миллиардов пар нуклеотидов. Ежесекундно в каждой клетке происходит более десяти миллионов химических реакций. Только работу синапсов, соединений между ста миллиардами нейронов, обеспечивает более ста разных нейромедиаторов, а количество всех химических соединений, участвующих в работе тела, исчисляется тысячами. Представление о теле как о несложном механизме, работу которого можно точно описать, а значит, легко исправить (как мы починили бы сломавшиеся часы), далеко от реальности. Такая сложность делает создание точной модели конкретного человеческого тела невыполнимой задачей.
Все достижения иммунологии и микробиологии не помогут предсказать с абсолютной точностью, заболеет ли человек после контакта с возбудителем инфекции. Несмотря на глубокое понимание физиологии и фармакологии, мы не сможем предугадать значение артериального давления конкретного пациента через час после введения лекарства с точностью хотя бы до десяти миллиметров ртутного столба. Лучшие генетики и биологи не дадут ответа на, казалось бы, относительно простой вопрос о точном будущем росте ребенка.
Но там, где детали сложного механизма от нас скрыты и точные предсказания невозможны, мы можем наблюдать за бросками кубиков. И, глядя на них, не только предсказывать вероятность того или иного результата, но и разглядеть связи между контактом с инфекцией и риском заболеть, лечением и шансами выздороветь, ростом родителей и вероятностью того или иного роста их детей.
Впервые статистическая связь двух параметров была продемонстрирована во второй половине XIX века английским ученым Фрэнсисом Гальтоном при попытке создать идеального человека.
На пути к сверхчеловеку
Не удивительно, что из всех известных миру научных проблем больше всего Фрэнсиса Гальтона интересовал вопрос наследственности. Он родился в 1822 году в семье, давшей Британии нескольких ученых и изобретателей, сам Чарльз Дарвин приходился ему двоюродным братом. С раннего детства Фрэнсис демонстрировал незаурядные способности: читал в два года, начал говорить на греческом и латыни к пяти, в шесть декламировал по памяти большие отрывки из Шекспира. В шестнадцать он ушел из школы, сочтя ее программу слишком узкой и неинтересной. По желанию родителей он поступил сначала в Лондонскую медицинскую школу, а затем учился в Кембридже математике, которую нашел более интересной, чем медицина.
Гальтон был полиматом – человеком, чей талант проявился сразу в нескольких областях. Он занимался метеорологией – ему принадлежит открытие антициклонов, психологией – Гальтон описал феномен синестезии, и криминалистикой – именно он продемонстрировал уникальность отпечатков пальцев, благодаря чему их начали использовать для идентификации личности. Кроме того, будучи неутомимым путешественником и членом Королевского географического общества, он дважды получал медали за картографические исследования Южной Африки.
Но главное увлечение Гальтона, идея, которой он был одержим в течение всей своей жизни, – улучшение людей. Гальтон хотел достичь этого тем же путем, каким в течение тысячелетий выводили новые породы домашних животных, – скрещивая людей, несущих нужные признаки. Конечно, речь не шла о принудительном скрещивании. Гальтон пропагандировал финансовую поддержку ранних браков между отпрысками семей с хорошей наследственностью и другие способы увеличить потомство у “правильных” семей.
Этим он положил начало евгенике – учению о применении селекции к человеку. На некоторое время она стала академической дисциплиной, преподавалась во многих университетах и получала солидное частное и государственное финансирование. Увы, относительно безобидные идеи Гальтона несли в себе разрушительное начало: через несколько десятков лет мир содрогнулся, узнав о евгенической программе нацистской Германии, стоившей жизни миллионам людей с “неправильной” наследственностью. Но во второй половине XIX века, задолго до Бухенвальда и Дахау, мысль об улучшении человечества путем отбора еще не казалась пугающей. Вызванный теорией эволюции и открытием законов наследования переворот в биологии воодушевлял и стимулировал использовать новое знание на благо человечества – или хотя бы отдельно взятой нации.
Для того чтобы лучше понимать принципы передачи признаков по наследству, Гальтон изучал связь между ростом взрослых детей и их родителей. Довольно быстро стало очевидно, что точно предсказать рост отдельного человека, опираясь на рост его родителей, невозможно. Никакие формулы не работали. Да и жизненный опыт подсказывал, что дети одних родителей, даже одного пола, растут очень по-разному. Значило ли это, что рост не относится к факторам, которые передаются по наследству?
Гальтон составил таблицу соотношения роста родителей и их детей. Вот как она выглядела. Цифры в таблице указывают, сколько людей в исследуемой Гальтоном группе из 928 человек имели указанный в верхней строке рост при указанном в левой колонке усредненном росте родителей.
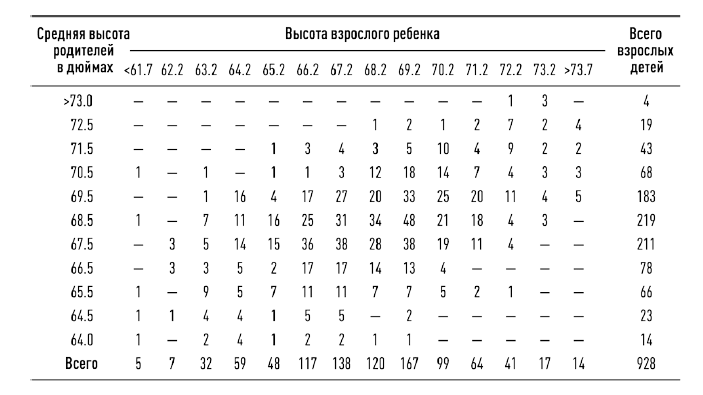
Распределение роста участников исследования Гальтона, как и вообще всех взрослых людей, населяющих Землю, было близко к нормальному. Как уже говорилось выше, нормальное распределение характерно для параметров, являющихся суммой большого числа независимых воздействий. Рост – типичный пример, поскольку формируется под разнонаправленным влиянием многих генов, эпигенетических факторов, факторов среды, перенесенных травм и болезней.
Интересно, что, если мы построим графики, используя цифры внутри каждой строки, мы тоже увидим колоколообразные кривые: рост детей, родившихся у родителей определенного роста, тоже распределен нормально. Но вершины этих колоколов находятся в разных местах: наиболее вероятный рост ребенка тем выше, чем выше средний рост его родителей. Если связать эти вершины, мы получим близкую к прямой линию.
Получается, что хотя точное вычисление роста человека по росту его родителей невозможно, связь между этими значениями существует. И ее можно описать достаточно простым уравнением, применяемым для линейных графиков. А затем использовать это уравнение для того, чтобы на основе одного из параметров предсказать наиболее вероятное значение второго. Гальтон назвал такую статистическую взаимосвязь корреляцией (от англ. co-relation, “взаимосвязь”).
Сейчас статистическую связь вычисляют, например, в эпидемиологии. Если заболевание и определенные факторы риска коррелируют, то мы можем предположить, что этот фактор и является причиной болезни.
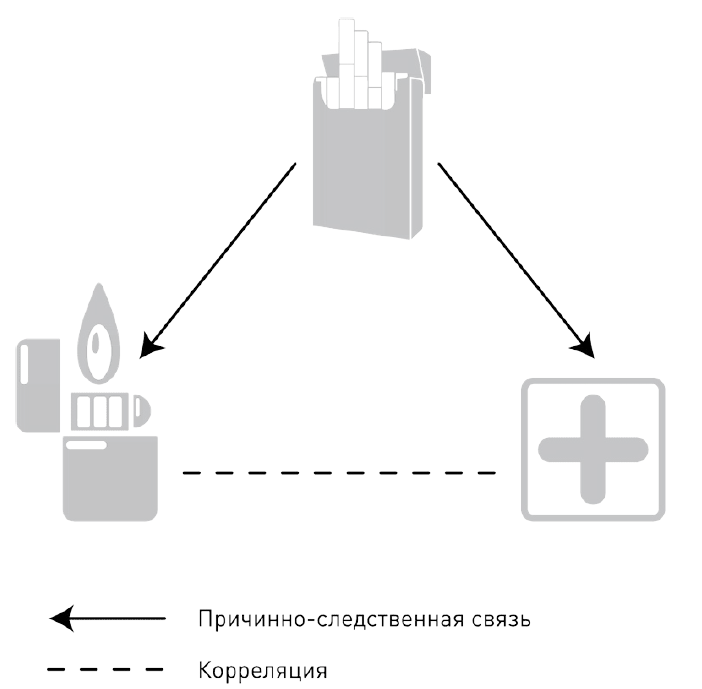
Но важно помнить, что статистическая связь не обязательно равна причинно-следственной. Оба коррелирующих параметра могут меняться под воздействием третьего фактора, называемого спутывающей переменной. Если мы исследуем два параметра – заболеваемость раком легких и наличие зажигалки в кармане – то наверняка обнаружим, что они взаимосвязаны: окажется, что люди с зажигалкой чаще болеют раком легких. Но это не значит, что рак легких вызывают зажигалки в кармане. Оба параметра будут зависеть от третьего – курения, который и является в этом примере спутывающей переменной.
А что насчет контролируемых клинических экспериментов? В них мы тоже имеем дело со сложными биологическими системами, а значит, исходы в каждой из групп не детерминированы и носят вероятностный характер. Значит, состояние пациентов в сравниваемых группах может меняться по-разному исключительно в силу случая. Как же тогда определить, случайна разница или вызвана действием лекарства?
Леди, пьющая чай
Прекрасным летним вечером 1919 года сотрудники Ротамстедской экспериментальной станции собрались в комнате отдыха. Было время традиционного для Англии вечернего чая – время отдохнуть и поговорить с коллегами о не связанных с работой пустяках. Новичок в компании, недавно принятый на работу молодой математик, вежливо наполнил чашку чаем, добавил в него молоко и протянул сидевшей рядом леди.
– Спасибо, Рональд, но я предпочитаю сначала наливать молоко и лишь потом добавлять чай, – сказала та.
– Вот ерунда, – удивился математик, которого звали Рональд Фишер, – уверен, что разницу почувствовать невозможно, что бы я ни налил первым, чай или молоко.
Но дама настаивала на своем. Конечно же, Рональд говорит глупости и она без труда определяет разницу на вкус. Спор быстро собрал вокруг пререкавшейся пары скучающих коллег, кто-то предложил поставить эксперимент, кто-то уже заключал пари.
Фишер задумался. Очевидно, что предстоит провести слепую дегустацию. Но перед началом эксперимента нужно решить несколько важных вопросов.
Во-первых, важно избежать ложноположительного результата – ситуации, когда правильные ответы дамы, вызванные простой случайностью, будут приняты за подтверждение ее способностей. Если мы совершим одну попытку и получим правильный ответ, это, конечно, не может служить доказательством: даже если она не различает последовательность приготовления чая на вкус, шансы на случайное угадывание достаточно велики, они равны ½. Пожалуй, мало будет и двух удачных попыток: хотя шансы уменьшатся вдвое и составят ¼, они по-прежнему значительны. Какое же минимальное количество попыток нужно для того, чтобы правильные ответы подтверждали способность леди? Три? Четыре? Пять? Еще больше?
Во-вторых, не менее важно избежать ложноотрицательного результата, то есть ситуации, когда вывод об отсутствии способности будет ошибочным. Угадывание не обязательно должно быть стопроцентным: одна ошибка не исключает того, что леди все равно справляется с задачей лучше, чем если бы давала случайные ответы. Какие же выводы делать, если неверным будет лишь один ответ из восьми? А если один из двенадцати?
И в-третьих, как и в любом контролируемом эксперименте, чашки должны отличаться только изучаемым параметром, и больше ничем. Значит, разной может быть только последовательность, в которой чай и молоко наливают в чашку. Любые различия в температуре, количестве молока, сахара, крепости чая, способные повлиять на результат, нужно исключить. Но ведь приготовить две абсолютно идентичные чашки чая все равно невозможно, и небольшие отличия неизбежны.
После некоторого размышления Фишер велел приготовить восемь чашек. В четыре из них налили сначала чай, а затем молоко. В остальные – наоборот. Это делалось в стороне, чтобы испытуемая не знала, что пробует. Чашки подносили одну за другой, в случайном порядке, и, после того как дама давала ответ, Фишер молча записывал результат. По свидетельствам очевидцев, дама дала правильный ответ в каждой из восьми попыток.
В 1935 году Рональд Фишер издал книгу “Дизайн эксперимента”, где привел в качестве примера эту давнюю историю. Фишера абсолютно не интересовала природа удивительной способности дамы. Он не назвал ни имен, ни места, где проводился эксперимент, – об этом мы знаем только со слов других участников. Все, что имело для него значение, – ответы на вопросы, которые он задавал себе перед чайным экспериментом.
Книга оказала огромное влияние на подход к проведению контролируемых экспериментов и оценке их результатов. Именно благодаря ей и другим работам Фишера статистика и теория вероятностей стали неотъемлемой частью исследований, в том числе и медицинских.
Объясняя чайный эксперимент, Фишер ввел представление о нулевой гипотезе. Нулевая гипотеза – это предположение, что между изучаемыми явлениями, в данном случае это порядок приготовления чая и ответы дамы, не существует связи, а в контролируемых экспериментах – что отличия между группами носят случайный характер. Она является гипотезой по умолчанию, и только если эксперимент опровергает ее, у нас появляются основания предполагать, что связь все-таки есть.
Для проверки нулевой гипотезы Фишер предложил использовать тест на статистическую значимость. Он определяет, какова вероятность получить наблюдаемые в ходе эксперимента значения при условии, что нулевая гипотеза верна. Эту вероятность называют p-значение (пи-значение) или просто p (пи). Фишер предложил считать, что нулевая теория может считаться опровергнутой, если p-значение меньше 0,05.
Фишер рассчитал, что если бы в эксперименте использовалось по три, а не по четыре чашки чая каждого типа, то случайное угадывание всех шести чашек происходило бы в одном случае из двадцати, то есть p как раз было бы равно 0,05, и выбранный критерий не выполнялся бы. Поэтому он предложил использовать минимум восемь чашек, по четыре каждого типа. Тогда при всех правильных ответах значение p равно одному к семидесяти, или 0,014 в десятичных дробях, что меньше выбранного порога. В таком случае результат признается статистически значимым.
Этот подход прочно закрепился в исследовательской практике, в том числе и в медицинских экспериментах. В контролируемых клинических испытаниях нулевая гипотеза гласит, что эффект у изучаемого метода отсутствует, а наблюдаемые различия исходов в сравниваемых группах случайны. В подавляющем большинстве работ вы увидите расчет значения p, и очень часто результат будет считаться статистически значимым, если значение p меньше 0,05.
Важно помнить, что упомянутый Фишером порог p = = 0,05 – условен и был предложен как условие джентльменского соглашения между учеными. Разница между убедительностью результатов с p = 0,04 и с p = 0,06, конечно, гораздо меньше, чем для результатов с p = 0,04 и p = 0,001, хотя первые находятся по разные стороны условной границы, а вторые – по одну. И Фишер, и другие математики подчеркивали, что критерий p < 0,05 недостаточно строг, не годится для медицинских исследований, и рекомендовали другие пороговые значения, 0,01 и 0,001, но исследователи ухватились за наименее строгое, а значит, проще всего достижимое.
Что касается исключения ложноотрицательного результата, Фишер отметил, что чем меньше размер эффекта, то есть чем слабее способность леди угадывать, в какой последовательности были налиты молоко и чай, тем больше чашек чая потребуется для того, чтобы ее выявить.
Для описания вероятности ложноотрицательного результата рассчитывают статистическую мощность эксперимента. Чем выше статистическая мощность, тем меньше вероятность того, что мы ошибочно подтвердили нулевую гипотезу. Статистическая мощность медицинского исследования возрастает с увеличением количества участвующих в нем пациентов. Хотя столь же распространенных, как p < 0,05, стандартов допустимой вероятности ложноотрицательного результата не существует, часто ориентируются на статистическую мощность не менее 0,80.
Таким образом, исследователи находятся между двумя возможными ошибками:
• ложноположительным результатом, когда мы ошибочно отвергаем нулевую гипотезу и думаем, что нашли эффект, хотя на самом деле его нет, – такие ошибки называют ошибками I типа, и они могут приводить к тому, что пациентов лечат бесполезными лекарствами и делают им бессмысленные операции;• ложноотрицательным результатом, когда мы ошибочно подтверждаем нулевую гипотезу и не замечаем реально существующий эффект, – такие ошибки называют ошибками II типа, и они чреваты незамеченными полезными или вредными эффектами лекарства.
Рандомизация – неслучайная случайность
Ответ на третий вопрос чайного эксперимента тоже имел далеко идущие последствия. Напомню, что Фишер задумался о том, как исключить влияние небольших отличий, которые неизбежно возникнут в процессе подготовки к тесту. В медицинских исследованиях эта проблема еще значимее: найти две группы людей, одинаковых во всех отношениях, куда сложнее, чем приготовить две одинаковые чашки чая.
Сравнимость групп – основа и необходимое условие контролируемого исследования. Пациенты разные, и болезнь у них протекает по-разному. Если в одной группе средний возраст пациентов ниже или болезнь изначально протекает легче, чем в другой, то после лечения состояние пациентов может различаться, даже если лекарство не работает. Возникает риск приписать препарату несуществующий эффект.
☛ Сравнение изначально разных групп может привести к достаточно контринтуитивным последствиям. Так, в 1986 году были опубликованы результаты сравнения эффективности разных методов лечения почечных камней. Авторы пришли к выводу, что чрескожная нефролитотомия эффективнее, чем открытая: в первом случае успешны были 83% (289 из 350) операций, а во втором – лишь 78% (273 из 350). Однако сравнение результатов удаления небольших (< 2 см) и больших (> 2 см) камней дало неожиданный результат. В обоих случаях открытая оказалась эффективнее. Для маленьких камней открытая была эффективна в 93% случаев против 87%. А для больших – в 73% случаев против 69%.Этот эффект называется парадоксом Симпсона, хотя никакого парадокса тут на самом деле нет. Причина в том, что удаление маленьких камней (суммарно 88% успешных операций) эффективнее, чем удаление больших (суммарно 72% успеха) при любом из методов. Пациентов распределяли между двумя видами лечения неравномерно: тем, у кого были маленькие камни, чаще назначали операцию с маленьким разрезом, а при больших – открытую. Поэтому среди тех, кого лечили чрескожной нефролитотомией, преобладали пациенты с маленькими камнями, а среди тех, кого лечили открытым методом, – с большими. Это и привело к иллюзии более высокой эффективности чрескожной нефролитотомии.
Устранить эту проблему можно, изначально создавая максимально похожие группы. Например, переместив часть пациентов из одной группы в другую или сразу набирая их так, чтобы все параметры, которые мы считаем важными, были распределены поровну. Можно исключить влияние пола, отбирая в обе группы только женщин. Или следить за тем, чтобы процент женщин в сравниваемых группах был примерно одинаков. Но предложенное Фишером решение намного изящнее и эффективнее. Его преимущество в том, что оно уравновешивает между группами даже факторы, о существовании которых мы не догадываемся.
Фишер впервые применил его, работая на той самой Ротамстедской экспериментальной станции, где проходило знаменитое чаепитие. Его пригласили в Ротамстед, чтобы разобраться с данными, накопленными за девяносто лет сельскохозяйственных экспериментов. Станция занималась сравнительным анализом урожайности сортов и эффективности органических удобрений. Эксперименты заключались в том, что каждый год сотрудники станции засевали поля разными сортами овощей и злаков и применяли разные смеси азотных и фосфатных солей, а когда приходило время урожая, взвешивали и записывали полученный результат. Результаты на разных полях сравнивали и между собой, и с тем, что было собрано на контрольном поле, которое не удобрялось.
Сотрудники станции понимали, что сравниваемые поля изначально отличаются. На одном почва могла быть питательнее, на другом – мог сказываться накопленный эффект примененных в предыдущие годы удобрений, третье могло получать больше влаги во время дождя, четвертое было лучше освещено, а на пятом было меньше насекомых-вредителей. Возникал неизбежный вопрос: если на втором поле собрали на 10% больше картофеля, чем на четвертом, можно ли считать, что дело в сорте картофеля или в удобрении, а не в особенностях поля? И не была бы разница такой же, если бы оба поля засеяли одним сортом и вообще не удобрили?
Для решения этой проблемы были придуманы индексы плодородности, которые высчитывали при помощи сложных формул, делая поправки на разные факторы. Однако каждая из сельскохозяйственных станций Великобритании выработала свои методы расчета и считала их единственно верными. К тому же сделать практические выводы из сложных вычислений было крайне непросто.
Изучив накопленные данные, Фишер предложил полностью изменить дизайн экспериментов. Он рассуждал так. Каждый квадратный фут земли отличается от остальных множеством параметров, которые невозможно точно измерить и учесть, как невозможно найти и два одинаковых поля. А значит, различия между сравниваемыми полями нужно каким-то образом уравновесить. Фишер предложил разбить все поля на множество маленьких участков и относить их к одной из групп эксперимента случайным образом. Например, решать, каким сортом картофеля будет засеян каждый из участков для сравнительного теста урожайности двух сортов картофеля, подбрасывая монетку. Результат будет выглядеть примерно так.
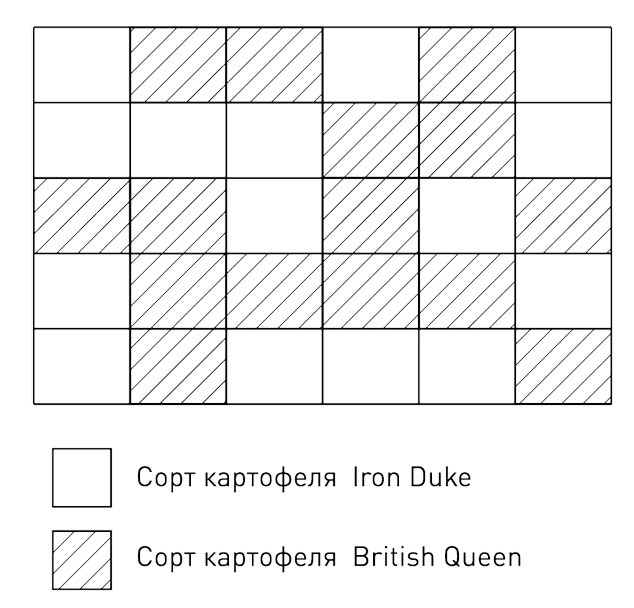
Плодородность разных частей поля может заметно отличаться. Но, поскольку мы сравниваем не две половины поля, а общий урожай на всех случайно разбросанных по полю участках, их плюсы и минусы достанутся каждому из двух сортов картофеля примерно поровну.
Чем больше количество участков, на которые мы делим поле, тем меньше различаются стартовые условия. При малом их количестве различия могут быть заметны, но даже в этом случае, объяснял Фишер, случайное распределение даст лучший результат, чем попытка сделать ручную поправку на множество факторов, в том числе неизвестных. Кроме того, случайное распределение создает математическую основу для дальнейших расчетов и позволяет определить размер возможной ошибки.
Метод случайного распределения по группам, названный рандомизацией (от англ. random – “случайный”), быстро прижился в сельском хозяйстве. Экспериментальные станции оценили его преимущества и охотно приняли на вооружение. Вскоре идеи Фишера пришли и в медицину.
Рандомизация в медицинских экспериментах
Сравнимость групп в медицинском эксперименте очень сильно зависит от способа, которым их создают. Худший из подходов – оставить распределение на усмотрение экспериментатора: это дает слишком много возможностей манипулировать результатами. Что мешает, например, отправить молодых пациентов в экспериментальную группу, а пожилых в контрольную? Это обеспечит и более быстрое выздоровление, и меньшую смертность в первой даже при абсолютно бесполезном лечении.
Когда группы создают таким образом, они часто отличаются по возрасту, полу, серьезности болезни и общему состоянию пациентов. Оценка эффективности лечения в подобных экспериментах завышена в среднем на 30–40%. Хотя исследователи могут быть напрямую заинтересованы в положительном результате и манипулировать составом групп осознанно, возможно и невольное влияние – скажем, если из сострадания к пациентам исследователь включает в экспериментальную группу тех, кому лечение нужнее, или тех, кому оно скорее поможет.
Сделать распределение пациентов не зависящим от экспериментатора пытались еще в XIX веке. Так, в 1809 году военный хирург Александр Гамильтон, проверяя эффективность кровопускания, поочередно принимал солдат сам или направлял к другим врачам, которые, в отличие от него, активно применяли этот метод. Примечательно, что смертность пациентов Гамильтона оказалась почти на порядок меньше, чем у его коллег.
Впоследствии экспериментаторы распределяли пациентов поочередно по списку, делили по первой букве имени, по месяцу или дате рождения. К началу XX века такой способ получил довольно широкое распространение и стал называться методом чередования. Хотя у него есть определенные преимущества – при достаточном количестве пациентов группы наверняка сравнимы, – по-настоящему надежен он лишь при условии, что врач строжайше придерживается процедуры.
Если же исследователь не является образцом кристальной честности или слишком сердоболен, метод чередования оставляет много возможностей влиять на состав групп. В первую очередь потому, что не все откликнувшиеся на предложение участвовать в эксперименте пациенты становятся в результате его участниками. Пациента сначала обследуют, чтобы подтвердить, что он соответствует критериям включения. Затем он беседует с врачом, который рассказывает об исследовании и возможных последствиях для здоровья, положительных и отрицательных. И лишь после этого, при условии согласия и самого пациента, и врача, пациент становится частью эксперимента. Если использовать метод чередования, врач всегда знает, в какой из групп окажется следующий участник. Ничто не мешает влиять на их состав, отказывая пациентам с более тяжелым течением болезни, чтобы включить в группу следующего, с более легким. Или повлиять в ходе беседы на готовность пациента принять участие. Единственный способ исключить подобные манипуляции – сделать распределение случайным и скрыть от исследователя его последовательность.
Первым рандомизированным клиническим испытанием (РКИ) с целенаправленным сокрытием последовательности распределения от врачей принято считать клиническое испытание стрептомицина в 1947 году. Оно было спланировано и проведено выдающимся эпидемиологом и статистиком Остином Брэдфордом Хиллом, входившим в состав созданной Советом по медицинским исследованиям Великобритании научной группы.
Открытие и начало массового производства пенициллина в 1941 году вызвало огромный интерес к изучению других природных антибиотиков. Полученный в 1944 году в США из актиномицетов стрептомицин оказался эффективен против устойчивого к пенициллину возбудителя туберкулеза Mycobacterium tuberculosis, называемого также палочкой Коха.
Туберкулез – опаснейшее инфекционное заболевание. Еще в XIX веке в России, Европе и Америке на каждые 100 тысяч жителей от него ежегодно погибало 400 человек. Хотя болезнь убивала медленно и не вызывала явных эпидемических вспышек, из-за количества погибших и неотвратимости гибели ее называли белой чумой. Среди погибших от туберкулеза были Антон Чехов, Роберт Льюис Стивенсон, Вольтер, Фредерик Шопен, Эдвард Григ, Джордж Оруэлл и многие-многие другие.
Несмотря на отсутствие методов лечения и профилактики, с середины XIX века смертность от туберкулеза начала постепенно снижаться. Некоторые исследователи объясняют это постепенным улучшением качества жизни, другие – тем, что человечество начало приспосабливаться к болезни и развивать сопротивляемость палочке Коха. Но хотя к середине XX века заболеваемость и смертность снизились на порядок, туберкулез оставался смертельной и неизлечимой болезнью.
Результаты первых испытаний стрептомицина на больных туберкулезом морских свинках были положительными, первые проведенные в США эксперименты на людях тоже обнадеживали. Поэтому Великобритания закупила некоторое количество стрептомицина и запланировала собственную проверку. В созданный для этого комитет вошли Остин Брэдфорд Хилл и уже известный нам по исследованию патулина Филип д’Арси Харт.
Хилл спланировал эксперимент, опираясь на идеи Рональда Фишера. Главным новшеством была замена поочередного распределения пациентов на случайное. В теории метод чередования решил бы задачу создания сравнимых групп. Но за время работы Хилл уже неоднократно наблюдал, как исследователи слегка корректировали распределение пациентов по группам, пытаясь увеличить шансы эксперимента на успех. Клиническое испытание проходило одновременно в нескольких клиниках. Для распределения по группам использовали таблицы случайных чисел, при этом “информация о последовательности распределения не была известна ни кому-либо из исследователей, ни координатору и хранилась в запечатанных конвертах, на которых были указаны лишь название больницы и номер”. Поскольку Хилл не планировал оценивать субъективные симптомы, он счел ослепление пациентов излишним. Но рентгенологи, смотревшие снимки легких, и микробиологи, высевавшие возбудителя болезни из мокроты пациентов, были должным образом ослеплены.
Результаты первых месяцев давали надежду, что лекарство от туберкулеза найдено. Через два месяца после начала приема стрептомицина в группе было отмечено значительное улучшение по сравнению с контрольной. Однако в последующие месяцы ситуация изменилась: смертность в группах сравнялась, и микробиологи по-прежнему высеивали возбудителя туберкулеза из мокроты получавших стрептомицин пациентов. Так, всего через несколько лет после открытия антибиотиков медицина столкнулась с феноменом резистентности. Увы, стрептомицин не подходил для монотерапии: резистентность к нему возникала слишком быстро. Зато позже он показал хорошие результаты при приеме с пара-аминосалициловой кислотой (ПАСК): резистентность в этом случае возникала намного реже.
Главное, что продемонстрировало это исследование: рандомизацию с сокрытием распределения от исследователей можно и нужно применять в медицинских экспериментах. Постепенно она стала частью так называемого золотого стандарта, идеального дизайна клинического эксперимента – двойных слепых рандомизированных клинических испытаний.
Впрочем, происходящее на практике часто далеко от идеала. Еще в 90-х годах XX века проверка качества рандомизации показывала, что только в трети опубликованных исследований использован надежный метод создания случайной последовательности распределения. И только в четверти сообщалось, что были предприняты хоть какие-то меры по ее сокрытию.
При этом не любой метод сокрытия достаточно надежен. До недавнего времени самым распространенным способом было использование кодов в непрозрачных запечатанных конвертах. Код указывает, в какую группу должен попасть пациент. Порядок, в котором конверты складывают в стопку, заранее генерируют в компьютерных программах или берут из готовых таблиц случайных чисел. Предполагается, что конверты будут вскрывать строго по очереди. Только после того, как пациент дал согласие на участие в клиническом эксперименте и его данные зафиксировали, очередной конверт можно вскрыть. Однако этот метод уязвим. Экспериментаторы прилагают немалые усилия, чтобы узнать содержание конвертов до того, как пациентов включат в исследование. Вот несколько простых рецептов.
В конце 90-х годов прошлого века был исследован гипотензивный препарат “Каптоприл”. В испытании участвовали 10985 пациентов в более чем пятистах больницах Финляндии и Швеции. “Каптоприл” был первым из нового класса препаратов, ингибиторов ангиотензинпревращающего фермента (ингибиторы АПФ), и на него возлагали очень большие надежды. В этом клиническом исследовании, названном Captopril Prevention Project (CAPPP), ингибитор АПФ впервые сравнивали с бета-адреноблокаторами, более старым классом гипотензивных препаратов.
Когда результаты опубликовали, некоторым специалистам бросилось в глаза, что группы отличались по росту, весу и исходным значениям систолического и диастолического давления. Конечно, отличия не были большими. Например, исходное артериальное давление отличалось на 2–3 мм рт. ст. Но шансы, что такая разница могла возникнуть случайным образом, были равны 1 к миллиону. Очевидно, процедура рандомизации с использованием запечатанных конвертов была нарушена. Расследование показало, что в некоторых клиниках исследователи вскрывали конверты еще до того, как очередной пациент был включен в испытание, а затем выбирали для каждого участника более, на их взгляд, подходящий код.
Если строгий контроль не позволяет вскрывать конверты заранее, приходится прибегать к помощи технологий: например, просвечивать конверты мощной лампой или обращаться за помощью к коллегам из радиологической лаборатории. Иногда конверты содержат не только код распределения, но и порядковый номер. В таких случаях незаметно изменить последовательность использования конвертов не получится. Однако если удалось выяснить последовательность, можно манипулировать очередностью приема пациентов, подгоняя ее под нужные группы. От этого не застрахуют ни порядковые номера, ни мешающая просвечиванию фольга. Самый отчаянный из зафиксированных способов узнать последовательность – ночное проникновение в кабинет ответственного сотрудника, чтобы порыться в его бумагах. Не самый высокоинтеллектуальный, но эффективный метод. К сожалению, все перечисленное выше – совсем не гипотетические способы манипулировать составом групп, а реально применявшиеся трюки.
Учитывая, как часто экспериментаторы применяют свои способности не для поиска научной истины, стоит подумать о еще одном уровне защиты. Например, зашифровать код распределения. Использование простых одинаковых кодов недостаточно надежно. Если вы использовали “А” для экспериментальной группы, а “В” – для контрольной, то чтобы вскрыть все распределение, достаточно знать, в какую группу попал один пациент. Этому препятствуют сложные уникальные коды. Лист, соотносящий каждый из кодов с конкретной группой, должен храниться в труднодоступном месте.
Лучшее из существующих сейчас решений – сервисы дистанционной рандомизации. Исследователь получает код для очередного пациента, связываясь с независимым сервисом по телефону или через интернет. Списки, соотносящие коды и группы, хранятся в рандомизационном центре и доступны только по окончании исследования либо в ситуациях, когда необходимо срочно выяснить, в какую группу попал пациент, – такая необходимость может возникнуть в случае опасного состояния, которое может оказаться побочным эффектом лечения.
Теоретически использование удаленных рандомизационных центров полностью лишает экспериментаторов возможности манипулировать составом групп. И пока практика подтверждает теорию. В ходе большого клинического испытания хирургической процедуры, которое проводили несколько не связанных между собой клиник, группы, получавшие лечение, оказались в среднем заметно моложе, чем плацебо-группы. Но разница наблюдалась только в тех клиниках, где использовали запечатанные конверты. У тех команд, которые применяли удаленную рандомизацию, возраст в группах не отличался. Впрочем, при большом желании подкуп рандомизационного центра решает и эту проблему.
☛ При соблюдении должных мер предосторожности рандомизация предотвращает предвзятость отбора. Однако всегда ли рандомизация справляется со второй задачей – созданием групп, схожих во всем, кроме лечения? Увы, даже после корректно проведенной рандомизации группы могут отличаться по важным показателям. Чем меньше пациентов мы рандомизируем, тем выше вероятность несхожести групп. В небольших исследованиях со 150–200 участниками это случается довольно часто. Чтобы избежать влияния этих различий на результат, после рандомизации группы сравнивают и при необходимости делают в ходе статистического анализа поправки. Отчет о клиническом исследовании обязательно должен включать информацию о том, насколько сравнимыми по важным параметрам получились группы в результате рандомизации.Другой метод решения проблемы – стратифицированная рандомизация. Ее суть в том, что сначала участников клинического испытания делят на страты – подгруппы, отличающиеся по важному признаку, например тяжести течения болезни. А затем внутри каждой страты проводят обычную процедуру рандомизации. В результате в экспериментальной и контрольной группах гарантированно оказывается одинаковое количество больных с определенной тяжестью заболевания.
Итак, рандомизация помогает создать сравнимые группы и препятствует осознанной манипуляции их составом. Но у нее есть и третья, не менее важная роль: она обеспечивает справедливость клинического испытания. Благодаря рандомизации каждый из участников имеет равный шанс получить возможные преимущества лечения или избежать возможных побочных эффектов. Поскольку клинические испытания проводятя на людях, вопросы этики имеют первоочередную важность. И не всегда на них можно получить простой и очевидный ответ.
Назад: Глава 6 Числа
Дальше: Часть третья Герои и мерзавцы