Глава 6
Столкновения черных дыр

В главах 3–5 мы говорили о черных дырах, находящихся вдали друг от друга, другими словами, об изолированных черных дырах. Нам было важно понять, как звезды обращаются по орбитам вокруг сверхмассивных черных дыр и как вокруг черных дыр образуются аккреционные диски – эти вопросы были и остаются очень интересными, так как именно такие явления наилучшим образом доказывают само существование черных дыр. Во всяком случае, это было так – до тех самых пор, пока детектор LIGO не зарегистрировал гравитационные волны от столкновения двух черных дыр, которое произошло более миллиарда лет назад на расстоянии в примерно столько же световых лет. В этой главе мы расскажем о теории, объясняющей наблюдавшееся событие. Что такое гравитационные волны? Почему сталкиваются черные дыры и почему эти столкновения порождают гравитационные волны? Почему прошло целых сто лет с тех пор, как Эйнштейн опубликовал свою общую теорию относительности, до момента, когда ученые сумели впервые прямо их зарегистрировать?

Столкновения черных дыр – самые мощные явления, какие только возможны в рамках общей теории относительности. Ни в каких других событиях во Вселенной не выделяется столько энергии. Большой взрыв, с которого началась история Вселенной, конечно, был еще мощнее, но для того, чтобы описать начало времени как такового, требуется еще более всеобъемлющая теория, чем общая теория относительности. И физики еще только нащупывают правильный теоретический подход, в рамках которого можно было бы дать полное описание Большого взрыва. Столкновения черных дыр не требуют создания более общих теорий, чем уже существующие: судя по всему, вполне достаточно просто уравнений Эйнштейна, G_µν = 8πG_NT_µν/c⁴. Более того, во многих случаях столкновений черных дыр мы, вероятно, можем не принимать во внимание тензор энергии-импульса T_µν, который обращается в нуль при отсутствии какого-либо вещества: полная энергия вещества вокруг черных дыр исчезающе мала по сравнению с энергией покоя самих черных дыр. Следовательно, чтобы описать столкновения черных дыр, нам надо всего лишь решить систему уравнений исключительно простого вида: G_µν = 0. На знаменитой фотографии Эйнштейна он как раз записывает эквивалентную систему R_µν = 0, где R_µν – так называемый тензор Риччи, тесно связанный с тензором Эйнштейна и по сути эквивалентный ему при отсутствии вещества. Правда, на фото (рис. 6.1) Эйнштейн пользуется индексами i и k, но это дело вкуса: он вполне мог бы написать и R_µν = 0.

Хоть мы уже и обсуждали эйнштейновские уравнения поля, но прежде чем приступить к подробному разбору столкновений черных дыр, стоит пересмотреть наши интуитивные представления о том, что эти уравнения описывают. Коротко можно сказать, что уравнения поля выражают в математической форме способ, которым вещество определяет искривление пространства-времени. Что уравнения поля позволяют пространству-времени делать, когда вещество отсутствует? Один из примеров разрешенных в этом случае состояний пространства-времени – это просто отсутствие какой-либо кривизны. Другими словами, совершенно плоское пространство-время является решением уравнений Эйнштейна в вакууме, но это решение не единственное. Действительно, есть и другой пример конфигурации пространства-времени, допускаемой уравнениями поля в вакууме: изолированная черная дыра. Как мы видели, внутри горизонта черной дыры могут существовать сингулярности или другие необычные особенности, которые можно было бы связать с ненулевым тензором энергии-импульса. Но снаружи горизонта вполне возможно полное отсутствие всякого вещества. У нас нет никаких обязательств по поводу внутренности черной дыры, так как оттуда до нас все равно не могут дойти никакие сигналы. Поэтому из соображений экономии проще всего считать, что изолированная черная дыра – это пример искривления пространства-времени даже и при отсутствии вещества. Пара черных дыр, обращающихся друг вокруг друга, дает нам еще один пример решения уравнений поля в вакууме. Такие черные дыры будут постепенно сближаться друг с другом по спирали и в конце концов сольются в быстро вращающуюся керровскую черную дыру. Именно такое событие и наблюдалось на установке LIGO 14 сентября 2015 года.

Рис. 6.1. Эйнштейн и уравнение поля в вакууме, полученное в рамках общей теории относительности. Это уравнение – частный случай уравнений Эйнштейна в отсутствие вещества.

Еще более важный класс решений уравнений поля в вакууме – гравитационно-волновые геометрии. Как мы уже объясняли в главе 1, гравитационные волны следует понимать в терминах, похожих на те, в каких Максвелл описывал свет. Вспомним, что свет – это распространяющаяся в пространстве волна электрического и магнитного полей, связанных между собой так, что пространственное изменение электрического поля влечет временное изменение магнитного и наоборот, в полном соответствии с максвелловскими уравнениями электромагнетизма.

Обычно мы представляем себе электрические поля возникающими от присутствия электрических зарядов, тогда как магнитные поля вызываются электрическими токами. Но в случае света электрическое и магнитное поля, однажды возникнув, продолжают распространяться вечно или, по крайней мере, до тех пор, пока не встретят на своем пути вещество, которое поглотит или рассеет световую волну. Гравитационная волна ведет себя точно так же: возмущение плоской метрики пространства-времени распространяется вечно, причем в соответствии с уравнениями поля в вакууме пространственноподобные изменения метрики вызывают времениподобные изменения.

Продолжим аналогию между гравитационной волной и светом немного дальше. Электромагнитные волны порождаются ускоряющимися электрическими зарядами. Например, в радиомачте во время работы в проводниках возбуждаются высокочастотные переменные токи. Эти токи являются не чем иным, как электрическими зарядами, ускоряющимися то в одном, то в другом направлении. Они порождают электрические и магнитные поля, которые затем распространяются во все стороны, чтобы быть принятыми нашими радиоприемниками. Радиоволны по сути являются тем же светом, только с более длинными волнами, и добиться излучения видимого света также можно ускорением зарядов то в одном, то в противоположном направлении. Подобным же образом гравитационные волны порождаются ускоряющейся материей. Обычной формой ускорения в гравитационных системах является центростремительное ускорение на круговых орбитах. Пример, которым мы подытожили главу 2, заключался в том, что двойные звездные системы порождают гравитационное излучение из-за орбитального движения звезд друг вокруг друга. Убыль энергии, уносимой из системы этим излучением, приводит к тому, что орбиты звезд начинают постепенно сближаться по спирали, и это сближение можно зарегистрировать. Тогда, вероятно, вас не слишком удивит и то, что и черные дыры, сближаясь по спирали друг с другом, тоже должны продуцировать гравитационное излучение. Однако, с философской точки зрения, в высшей степени удивительно, что гравитационное излучение может выходить из системы, в которой нет ничего, кроме пустого пространства (под словом «пустое» мы подразумеваем, что оно является решением уравнений поля в вакууме). Этот парадокс заставляет нас вспомнить уже высказанную нами ранее мысль: тяготение само по себе притягивает!

Гравитационные волны, зарегистрированные установкой LIGO, кто-то сравнил со звуком; возможно, самую большую известность из всех высказываний руководителей группы LIGO приобрело то, в котором они назвали щебет и стук, которые они услышали, переведя гравитационные волны в звуки (а частота принятых гравитационных волн случайно совпала именно с характерной для звуковых волн частотой в пару сотен герц), «музыкой космоса». Эта аналогия остроумна и глубока, но здесь мы хотели бы подчеркнуть как раз отличие гравитационных волн от звуковых. Звук – распространяющаяся в воздухе волна сжатия. Это означает, что звук состоит из перемежающихся областей высокого и низкого давления, распространяющихся сквозь массу воздуха. Отдельные молекулы газов, из которых состоит воздух, находятся в состоянии постоянного хаотического теплового движения, но «поверх» этих сложных случайных движений участие в звуковой волне заставляет эти молекулы в среднем то подаваться немного вперед к слушателю, когда они вступают в область высокого давления и оно толкает их вперед, то немного сдавать назад от слушателя, когда область низкого давления отсасывает их назад. Это пример продольной волны: здесь слово «продольный» отражает тот факт, что внутреннее движение молекул, составляющее волну, происходит в направлении «вперед-назад» вдоль одной и той же продольной оси, которая определяется направлением распространения волны звука. В отличие от этого, обычный пример поперечной волны – это волна на струне, натянутой горизонтально. Если ударить по одному из концов струны молоточком сверху вниз, можно будет увидеть, как это вертикальное колебание бежит по струне в горизонтальном направлении. Слово «поперечный» обозначает, что внутреннее, локальное движение струны, составляющее собственно волну (в описанном нами примере вертикальное) происходит перпендикулярно к направлению распространения волны (горизонтальному). Гравитационные волны (и световые тоже) – это волны поперечные. Интересно, что, как следует из вышесказанного, при взрыве, где все вещество ускоряется во внешнем направлении в форме идеальной сферической оболочки, никакого гравитационного излучения не возникает. Пытаться таким способом породить гравитационную волну было бы похоже на попытку создать вертикальное поперечное колебание натянутой струны, просто натягивая ее туже, вместо того чтобы стучать по ней молоточком или щипком оттягивать вниз. Со звуком все совершенно иначе: при взрыве разлетающаяся во все стороны оболочка породила бы оглушительный грохот – именно потому, что при взрыве движение происходит в том же направлении вовне, в каком распространяется и сам звук.

Еще более существенное различие между звуком и гравитационной волной заключается в том, что звуку требуется среда, в которой он мог бы распространяться. Обычно это воздух, но звук может распространяться и в воде, и в твердом веществе. Но в вакууме звука не существует. А свет может распространяться в вакууме, и гравитационные волны тоже. По современным представлениям, средой для гравитационной волны является пространство-время, аналогично тому, как для звуковой волны средой является вещество. С этой точки зрения именно поперечный характер гравитационных волн, а вовсе не присутствие или отсутствие материальной среды как таковой, отличает их от звуковых.

Поперечность гравитационных волн принципиально определяет устройство для их регистрации, детектирования. Потому давайте попробуем сосредоточиться и представить себе, как «выглядит» гравитационная волна. Для лучшей визуализации представим себе, что она распространяется в направлении детектора LIGO в Ливингстоне, штат Луизиана, вертикально сверху вниз. Гравитационная волна не представляет собой ничего, кроме возмущения пространственно-временной метрики, поэтому все, что она может делать, – это менять расстояния. Чтобы разобраться в том, как она это делает, представим себе, что на месте детектора LIGO мы установили трехмерную кубическую решетку измерительных устройств, снабженных синхронизированными часами, так что, обмениваясь световыми сигналами, эти устройства могут отслеживать временны́е изменения пространственных расстояний между ними. (Возможно, ученые, работающие на установке LIGO, делали бы именно это, если бы им позволял бюджет!) Когда гравитационные волны отсутствуют, конфигурация устройств остается неизменной. Что происходит, когда приходит волна? Прежде всего, надо осознать, что вертикальные расстояния вообще не изменятся: гравитационная волна поперечна, а наша волна распространяется вертикально вниз. Однако в горизонтальном направлении «север-юг» расстояния между устройствами сначала увеличатся до некоторого максимального удаления, а потом уменьшатся до минимального, и так будет происходить с каждым новым циклом приходящей волны. В направлении «восток-запад» будут наблюдаться такие же изменения расстояний, но в фазе, в точности противоположной изменениям расстояний в направлении «север-юг». Другими словами, гравитационная волна одновременно растягивает пространство в направлении «север-юг» и сжимает его в направлении «восток-запад», а потом наоборот.

Детектор LIGO в Ливингстоне гораздо проще нашей воображаемой кубической решетки измерительных устройств. Одно его плечо тянется на 4 километра, отклоняясь на несколько градусов к востоку от направления строго на юг по мере удаления от центрального узла установки, а другое – на 4 километра под прямым углом к первому, отклоняясь на несколько градусов на юг от направления строго на запад. Для наших целей точные направления плеч не имеют значения, поэтому в этом пояснении будем считать, что они идут точно на юг и на запад. Не будет слишком большой идеализацией сказать, что, в сущности, LIGO представляет собой три измерительных устройства такого же типа, как мы описали в предыдущем абзаце: одно в центральном узле и по одному на конце каждого плеча. И вся виртуозная лазерная интерферометрия, на основе которой работает установка LIGO, может в идеале быть представлена как обмен световыми сигналами между устройствами с целью проследить, как будут меняться с течением времени расстояния между ними. В действительности LIGO фиксирует изменения со временем не абсолютных расстояний, а разностей расстояний вдоль двух плеч установки. Короче говоря, LIGO измеряет пространство-время в гораздо меньших подробностях, чем наша воображаемая кубическая батарея измерительных устройств, но все же этого вполне достаточно, чтобы зарегистрировать структуру сжатий и растяжений пространства, обусловленных гравитационной волной такого типа, какой мы описали в предыдущем абзаце.

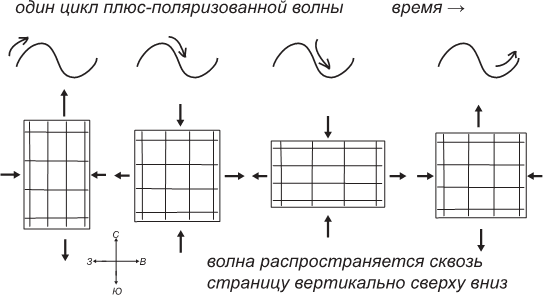
Рис. 6.2. Прохождение гравитационной волны через кубическую решетку. Во всех точках решетки можно представить себе детекторы, которые измеряют изменения расстояний между элементами решетки с течением времени.

Теперь предположим, что к нам приходит гравитационная волна, которая растягивает пространство-время по оси «северо-запад – юго-восток», одновременно сжимая его по оси «северо-восток – юго-запад». Понятно, что гравитационные волны такого типа должны быть столь же обычным явлением, как и волна, которую мы рассматривали до этого. Мы будем называть структуру сжатий и растяжений, ориентированную вдоль направлений «север-юг» и «восток-запад» плюс-поляризованной волной, а структуру, ориентированную вдоль осей «северо-запад – юго-восток» и «северо-восток – юго-запад» – кросс-поляризованной. Эти названия происходят просто от внешнего сходства этих структур с символами + и × соответственно. Иначе говоря, структура плюс-поляризованной волны – это повернутая на 45° кросс-поляризованная волна.

А теперь внимание! Установка LIGO в Ливингстоне кросс-поляризованных гравитационных волн просто не видит! Это происходит оттого, что структура кросс-волны не меняет разностей расстояний вдоль плеч, ориентированных с севера на юг и с востока на запад. Когда кросс-волна попадает на детектор, меняется – увеличивается и уменьшается – только угол между плечами, причем на нерегистрируемо малую величину. Но, к счастью, большая часть гравитационного излучения не является ни чисто кросс-поляризованной, ни плюс-поляризованной, а представляет собой некоторую смесь этих ориентаций. Поэтому чувствительность установки LIGO в Ливингстоне только к одной из двух возможных ориентаций волны ничуть не является ограничением, как могло бы показаться. Вспомним, что мы решили рассматривать только гравитационные волны, приходящие в строго вертикальном направлении, – на деле, конечно, они могут приходить с любой стороны. Таким образом, чувствительность установки LIGO в Ливингстоне к гравитационным волнам фактически зависит и от их направления, и от «поляризации»; то же самое можно сказать о детекторе LIGO в Хэнфорде, штат Вашингтон. Эта ситуация не слишком отличается от той, что была характерна для старинных уголковых (V-образных) телевизионных антенн, которые иногда приходилось осторожно поворачивать и наклонять, чтобы поймать сигнал лучшего качества.

Итак, предмет измерений обоих детекторов LIGO очень простой: это разности расстояний вдоль двух плеч. Но эти измерения делаются с невероятной точностью. Например, когда LIGO достигнет планируемого окончательного уровня чувствительности (что ожидается примерно в 2018–2020 годах), он будет способен измерять изменения в расстоянии в 10^–19 метров! Это одна десятитысячная часть диаметра протона! Такая фантастическая точность необходима, так как растяжение и сжатие пространства-времени гравитационными волнами чрезвычайно мало. Например, движение Меркурия по орбите вокруг Солнца тоже создает гравитационные волны, но LIGO не может их зарегистрировать не только потому, что они слишком слабые, но и потому, что их частота слишком низка, чтобы LIGO мог их почувствовать. До 14 сентября 2015 года не существовало измерительного устройства достаточно чувствительного, чтобы заметить вообще какие бы то ни было гравитационные волны. Путь к первой их регистрации был длинным и тернистым: множество ученых во всем мире десятилетиями пытались разработать все более и более чувствительные детекторы гравитационных волн. Сейчас, на заре эры гравитационно-волновой астрономии, LIGO способен зарегистрировать только катаклизмические события, такие как слияние черных дыр. Но есть надежда, что когда чувствительность приемников гравитационных волн улучшится, мы сможем, наконец, принимать и более слабые сигналы, такие как гравитационные волны от столкновений нейтронных звезд. Таким образом, изучение гравитации демонстрирует нам одно из глубоких противоречий природы: с одной стороны, это единственная сила, способная преодолеть все другие и привести к образованию черных дыр, а с другой – она оказывается настолько слабой, что гравитационное «эхо», возбуждаемое даже столь грандиозными событиями, как столкновение нейтронных звезд, все еще остается недоступным для регистрации нашими самыми чувствительными измерительными приборами.

Сделаем теперь небольшую паузу, чтобы подытожить все, что мы узнали к настоящему моменту о столкновениях черных дыр и об их регистрации. Суть проста: все, что мы делаем, – это исследуем решения уравнений Эйнштейна в вакууме G_µν = 0. Но, как мы сейчас объясним подробнее, беда в том, что на практике эти уравнения решить крайне трудно. Решения, которые нас интересуют, описывают сближение двух черных дыр по спирали, их слияние и сопутствующее этому процессу испускание гравитационного излучения. Это излучение распространяется через пространство-время и регистрируется установкой LIGO в виде пространственно-временной деформации: расстояния слегка сжимаются в одном направлении и растягиваются в другом, перпендикулярном первому, а затем растягиваются в первом направлении и сжимаются во втором. Что мы хотим к этому добавить? Мы хотим теперь дать более полное описание того, что происходит при столкновениях черных дыр и как это описание в рамках общей теории относительности преобразуется в практические методы, используемые в детекторе LIGO для поисков гравитационных волн.

Выражение «столкновение черных дыр» может вызвать в воображении вполне естественную картину: две черные дыры несутся друг к другу и сталкиваются лоб в лоб. В принципе, такое событие могло бы произойти, и даже сопровождалось бы сильным гравитационным излучением, но вероятность его, по-видимому, крайне мала. Дело в том, что черные дыры (к счастью для нас!) не так уж часто встречаются во Вселенной и их разделяет громадное в сравнении с их размерами пространство. Даже в густонаселенных областях, таких как шаровые скопления, в ядрах которых может содержаться по нескольку сотен черных дыр и среднее расстояние между ними должно составить всего лишь около светового месяца, такие столкновения могут случаться раз в миллиард лет, а то и реже. Повторим: крайне маловероятно, чтобы две черные дыры случайно оказались на встречных курсах и столкнулись лоб в лоб.

Гораздо более обычной является ситуация, когда в двойной звездной системе обе звезды достаточно массивны, чтобы в конце своей жизни коллапсировать в черные дыры. В результате из двойной звезды образуется двойная черная дыра. Это не значит, что в такой системе черные дыры сразу сольются друг с другом, но в конечном счете они обречены на это, потому что не обладают достаточной скоростью, чтобы преодолеть притяжение друг друга. Сначала они просто будут обращаться по своим орбитам друг вокруг друга, а точнее, вокруг общего центра масс. Для определенности примем, что рассматриваемые нами черные дыры похожи на те, сигнал от которых приняла установка LIGO 14 сентября 2015 года. Чтобы еще больше упростить наши рассуждения, будем считать, что каждая из этих черных дыр имеет массу в 32 солнечных, а начальное расстояние между ними равно 384 000 километров – среднему расстоянию от Земли до Луны. Предположим также, что ни одна из черных дыр не имеет заметного вращения, так что когда расстояние между ними велико, каждая из них хорошо описывается решением Шварцшильда. И пусть каждая из них обладает сферическим горизонтом событий радиусом 95 километров. Тогда медленное спиральное сближение их орбит в результате потерь энергии на гравитационное излучение займет около 210 лет и закончится в момент соприкосновения их горизонтов. Чем больше первоначальное расстояние между черными дырами, тем медленнее (и, значит, дольше) будет происходить сближение, причем это замедление пропорционально четвертой степени начального расстояния. Другими словами, если бы черные дыры из нашего примера первоначально находились вдвое дальше друг от друга, их спиральное сближение продолжалось бы в 16 раз дольше. Отсюда становится ясно, что спиральное сближение начинается медленно и становится быстрее и быстрее по мере приближения черных дыр друг к другу. Ранние стадии сближения черных дыр, зарегистрированных установкой LIGO, возможно, продолжались миллиарды лет! А конечная фаза, сигнал от которой и принял детектор LIGO, продолжалась, как мы вскоре увидим, всего несколько миллисекунд.

Частота гравитационных волн, излучаемых двойной черной дырой, которую мы здесь обсуждаем, равна удвоенной частоте орбитального вращения пары. Вначале эта частота очень низкая, но по мере того как черные дыры сближаются по спирали, она растет, так как, сближаясь, черные дыры обращаются друг вокруг друга все быстрее и быстрее. На первый взгляд выглядит парадоксально, что потери энергии на гравитационное излучение не замедляют, а, наоборот, ускоряют движение черных дыр по орбите. Это происходит потому, что должен соблюдаться баланс потенциальной и кинетической энергии: когда черные дыры сближаются, их гравитационная потенциальная энергия падает настолько быстро, что они способны одновременно и увеличивать свою кинетическую энергию, и излучать гравитационные волны.

Постепенное увеличение частоты гравитационного излучения играет важную роль в методе, которым детектор LIGO ищет сталкивающиеся черные дыры. LIGO чувствителен к частотам гравитационных волн в диапазоне от 30 до 1000 герц; звуковые волны такой частоты попадают в диапазон человеческого слуха. Поэтому, безотносительно к нашему обсуждению поперечных и продольных волн, теперь понятно, почему исследователи, работающие на LIGO, говорят, что, принимая гравитационные волны, они «слушают голос Вселенной». «Голос» двойной системы черных дыр, которую мы обсуждаем, в начале их спирального сближения звучит на частоте 30 Герц (глубокий низкий контрабас) при расстоянии между объектами в 990 километров, всего за 290 милисекунд до слияния. На этой стадии черные дыры носятся друг вокруг друга со скоростью 47 000 километров в секунду, немного более 15 % скорости света. Но частота быстро растет, и когда начинается слияние, она составляет примерно 190 Герц («соль» малой октавы, примерная частота обычного человеческого голоса). В этот момент черные дыры мчатся уже со скоростями около 86 000 километров в секунду, что составляет почти треть скорости света. Горизонты событий сливаются в единую структуру, напоминающую по форме вращающуюся арахисовую скорлупу.

Читателю может прийти в голову, что этот диапазон частот – от десятков до сотен герц – лишь немного ниже частот квазипериодических осцилляций, упоминавшихся в связи с источником Cyg X-1. Есть ли здесь связь? Конечно, есть! Вспомним, что диапазон частот в несколько сотен герц, соответствующий шкале времени в несколько миллисекунд, характеризовал самую короткую шкалу времени переменности рентгеновского излучения аккреционного диска в Cyg X-1, и объяснялось это тем, что эта шкала времени должна соответствовать орбитальному периоду частиц на ISCO-орбите черной дыры в системе Cyg X-1. Похожим образом немного более низкий диапазон частот, соответствующий несколько большему масштабу времени, характеризует бешеный вихрь вертящейся друг вокруг друга пары черных дыр массой в 32 Солнца на пороге их слияния. Памятуя о «теореме об отсутствии волос», мы интуитивно представляем себе, чего следует ожидать, как только горизонты событий черных дыр сольются: черная дыра неправильной арахисовидной формы должна упорядочиться и превратиться в слегка сплющенную сфероидальную керровскую черную дыру. Этот процесс называется «затуханием», но поначалу он идет довольно бурно. В ходе него излучаются гравитационные волны на многих частотах, но самые сильные из них имеют частоту 300 герц («ре» первой октавы). Волна затухания быстро идет на спад: каждые 8,6 миллисекунды амплитуда вибраций падает в 10 раз. Поэтому через 8,6 миллисекунды после слияния колебания вдесятеро слабее, чем при слиянии, через 17 миллисекунд – в 100 раз слабее, через 26 миллисекунд – в тысячу, и т. д. Выходит, что за долю секунды вибрации продукта слияния угасают, и он становится идеально спокойной керровской черной дырой.

Подведем краткий итог: гравитационные волны порождаются в ходе длительного и постепенного спирального сближения компонентов двойной черной дыры до момента, когда горизонты черных дыр сливаются и происходит затухание вибраций образовавшейся единой черной дыры до стационарного керровского решения. При этом самое мощное гравитационное излучение, намного превосходящее по интенсивности все предшествовавшее, испускается в интервале нескольких миллисекунд до и после момента слияния. Частота этого излучения лежит в звуковом диапазоне, меняясь от низкого «урчания» до финального звонкого «вскрика». Форма волнового фронта в целом соответствует тому, что мы называем «гравитационно-волновым чириканьем», и в области звуковых частот, в которой в основном и лежит зона чувствительности приемника LIGO, оно длится всего долю секунды. Столкновения черных дыр большего размера давали бы «чириканье» более низкого тона – при слиянии черных дыр с массой, значительно превосходящей 60 Солнц, оно было бы уже слишком низкочастотным, чтобы LIGO мог его услышать. И наоборот, при слиянии менее массивных черных дыр «чириканье» было бы более длительным и частоты его лежали бы в диапазоне чувствительности LIGO, а заканчивалось бы оно более пронзительным «взвизгом». Высота тона «чириканья» связана с общей массой сливающихся черных дыр, потому что оно исходит с уровня последних нескольких витков перед слиянием, а продолжительность нахождения на этих орбитах пропорциональна радиусу последнего горизонта, в свою очередь, пропорционального общей массе объектов.

Первое событие, которое зарегистрировала установка LIGO, произошло более миллиарда лет назад. Это достаточно много для того, чтобы, благодаря расширению Вселенной, то есть эффекту, подобному доплеровскому красному смещению, профиль волны сместился в «красную» сторону почти на 10 %. Другими словами, к моменту, когда гравитационно-волновое «чириканье» достигло Земли, оно звучало так, как если бы «чирикали» черные дыры на 10 % более тяжелые, чем те, что слились на деле. Вы могли бы спросить: как же мы можем отличить десятипроцентное красное смещение «чириканья», возникшее благодаря огромному расстоянию до черных дыр, от понижения тона «чириканья», обусловленного тем, что черные дыры оказались бы на 10 % более массивными и настолько же более близкими к нам? Ответ в том, что амплитуда сигнала от расположенных ближе к нам черных дыр была бы гораздо больше. Амплитуда обратно пропорциональна расстоянию. Поэтому если из наших главных принципов (то есть решая эйнштейновские уравнения поля в вакууме) мы вычислили интенсивность и частоту «чириканья», издаваемого сливающимися черными дырами, то по интенсивности и частоте принимаемого «чириканья» мы можем судить и о расстоянии до места слияния, и об общей массе сливающихся объектов.

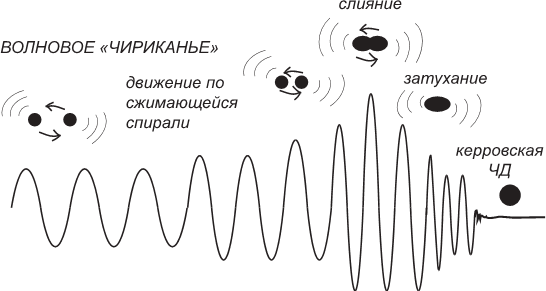
Рис. 6.3. Форма гравитационного волнового импульса («чириканья»), распространяющегося от двух сталкивающихся черных дыр.

Несмотря на гигантские потери энергии на гравитационное излучение, у конечного продукта слияния черных дыр остается еще внушительное количество энергии в форме быстрого вращения. Насколько быстро вращается образовавшаяся черная дыра, зависит еще и от того, как вращались две исходных черных дыры. В нашем примере они изначально были невращающимися, и поэтому образовавшаяся новая керровская черная дыра имеет спин до 70 % от максимального, допускаемого общей теорией относительности. Ее масса равна 61 солнечной, так как гравитационные волны унесли в виде энергии эквивалент еще трех масс Солнца. Общая энергия при использовании формулы E = mc²сохраняется: мы начали с 32 + 32 = 64 солнечных масс, а закончили 61 солнечной массой результирующего продукта слияния плюс три солнечные массы, унесенные гравитационным излучением. Таким образом, в гравитационное излучение переходит около 5 % общей массы двойной системы, причем подавляющая часть этой энергии излучается на нескольких последних орбитальных витках, в момент слияния и на стадии затухания. Сама по себе пятипроцентная доля выглядит не очень впечатляюще. Однако мощность (то есть скорость высвобождения этой энергии) оказывается почти непредставимой: этот эквивалент трех Солнц выделился в виде энергии в течение доли секунды, а пиковая светимость достигла 4 × 10⁴⁹ ватт. Нелегко вообразить это число, поэтому давайте вспомним следующее: светимость Солнца составляет 4 × 10²⁶ ватт, что примерно в 20 триллионов раз больше энергии, которую потребляет все человечество за секунду. В нашей Галактике около 100 миллиардов звезд, а в наблюдаемой Вселенной около 100 миллиардов галактик. Если в грубом приближении принять, что у каждой звезды светимость примерно равна солнечной, то общая светимость всех звезд Вселенной составляет примерно 10 000 миллиардов миллиардов Солнц. Так вот, эта мощность едва доходит до одной десятой энергии, выделяемой парой черных дыр в последние несколько миллисекунд их слияния! Таков масштаб катаклизма, необходимого для того, чтобы вызванную им «рябь» пространства-времени оказалось возможным измерить на Земле.

Но разве такая колоссальная энергия в точке своего выделения не сможет разорвать ткань пространства-времени в клочья? Возможно, стоит сформулировать этот вопрос не в таких легкомысленных выражениях; говоря серьезнее, не может ли возбуждение столь мощных вибраций в геометрии пространства и времени привести к образованию новых сингулярностей, «одетых» или «голых», помимо тех, что уже существуют в столкнувшихся черных дырах? Ответ на этот вопрос будет отрицательным: несмотря на всю свою мощь, гравитационные волны все равно недостаточно сильны, чтобы сделать это. Вот если бы была достигнута светимость в 4 × 10⁵² ватт – так называемая планковская светимость, которую можно вычислить, получив из ньютоновской гравитационной постоянной и скорости света в величину с размерностью мощности, – тогда ответ мог бы быть и другим.

Насколько же в итоге велики вибрации пространства-времени, вызванные слиянием черных дыр? В непосредственной близости к двойной системе было бы очень трудно сказать, какой аспект изменений геометрии мог бы быть приписан действию гравитационной волны, а какой следовало бы просто ассоциировать с движением двух черных дыр. На расстояниях больших, чем примерно десятикратный радиус последней устойчивой орбиты, становится уже возможным ясно различить плюс- и кросс-поляризованные гравитационные волны, описанные выше, – и конечно, оба этих типа волн здесь присутствуют. Отойдем теперь на 5000 километров от точки слияния, что примерно в 50 раз больше радиуса последней орбиты. На этом расстоянии максимальное относительное растяжение-сжатие составит примерно 0,3 %. Представим себе, что Алиса, шести футов ростом, присутствует там и наблюдает за событием. От макушки до пят она будет растягиваться и сжиматься приблизительно на пятую часть дюйма – на полсантиметра, и это растяжение-сжатие легко будет измерить, хотя это вряд ли будет ей приятно. И это совсем не то, что происходит с установкой LIGO – здесь, на Земле, на расстоянии примерно в миллиард световых лет. Из-за огромного расстояния амплитуда растяжения-сжатия будет меньше, чем то, что произошло бы с Алисой, примерно в 2 × 10¹⁸ раз. Вот потому-то установка LIGO и была спроектирована так, чтобы иметь такую до смешного высокую чувствительность: быть в состоянии измерить изменение длины в одну десятитысячную размера протона на расстоянии в четыре километра.

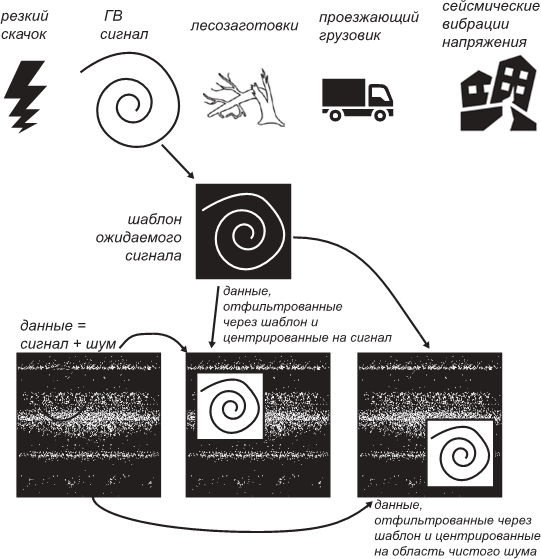
Рис. 6.4. Как шаблоны могут помочь выявить сигнал, утонувший в шумах.

Когда шаблон центрирован на сигнал, воспроизводится ясный и устойчивый рисунок шаблона, а когда он центрирован на шум, возникает картина, состоящая из беспорядочно разбросанных пятен. Аббревиатура ГВ означает «гравитационная волна».

Раз уж мы снова вспомнили о невероятной чувствительности LIGO, посвятим ей еще немного времени: в работе детекторов, подобных LIGO, есть одна не упоминавшаяся нами до сих пор важная особенность. Дело в том, что шумы, то есть все факторы, из-за которых расстояния вдоль измерительных плеч вибрируют и этим мешают различить вибрации гравитационных волн, в установке LIGO довольно велики. Только при очень редких, очень «громких» событиях, как раз таких, как столкновение черных дыр, зарегистрированное 14 сентября 2015 года, сигнал бывает различим на фоне этого шума. Но LIGO может измерить и сигналы, находящиеся под уровнем шума: для этого разработаны хитроумные методы анализа данных на основе того, что называется «библиотеками шаблонов»: обширные коллекции теоретических форм сигнала для всевозможных видов гравитационных волн, которые могут прийти на LIGO. Можно сравнить такой шаблон с уникальным «отпечатком пальцев» события, в том числе и такого, как спиральное сближение двух невращающихся черных дыр с массой в 32 солнечных. Источники шума: дрожание почвы, вызванное проезжающим по окрестному шоссе грузовиком или лесозаготовками вблизи городка Ливингстон, где расположена установка LIGO, тоже обладают своими характерными «отпечатками пальцев», и их форма отличается от тех, что свойственна «чириканью» сливающихся черных дыр. Детектор LIGO постоянно бомбардируется шумом, и поэтому то, что он измеряет, представляет собой смесь всех этих шумовых «отпечатков пальцев», наложившихся друг на друга вместе с появляющимися то здесь, то там «отпечатками» гравитационных волн. Таким образом, шаблон действует как маска, пропускающая через себя «отпечаток пальцев» гравитационной волны, который этому шаблону в точности отвечает, и в то же время блокирующая не соответствующие ему «отпечатки» шумовых сигналов. Хотя с помощью этой методики и нельзя полностью избавиться от влияния шума, она очень помогает – во всяком случае, достаточно для того, чтобы детектор LIGO улавливал гравитационно-волновые события, происходящие на невообразимых расстояниях от Земли.

Чтобы установка LIGO полностью реализовала свой потенциал в качестве гравитационно-волновой обсерватории, когда она достигнет планируемого уровня чувствительности, придется (и сейчас уже приходится) преодолевать некоторые дополнительные трудности, связанные с методом шаблонов. Первая из них заключается просто в вычислении всех возможных шаблонов формы сигнала для столкновений черных дыр и других событий, способных быть источниками гравитационных волн: столкновений между черными дырами и нейтронными звездами, слияний двух нейтронных звезд, вспышек сверхновых. Гравитационные волны могут приходить от быстровращающихся нейтронных звезд с выпуклостями на поверхности, из космического «океана» первичных гравитационнных волн, порожденных на заре эволюции Вселенной, и, наконец, возникать при разрывах, перекручивании и пересечениях в сети космических струн, которые, согласно гипотезам некоторых космологов, составляют основу Вселенной. Решать эйнштейновские уравнения поля во всех этих разнообразных ситуациях – задача не из легких, но делать это необходимо, чтобы построить требующиеся для работы LIGO шаблоны. Труднее всего в этом отношении иметь дело со столкновениями. Но после нескольких десятилетий совместных усилий десятков исследователей теоретически задача слияния двойных черных дыр теперь в целом решена. Этого удалось достичь, сочетая аналитические методы (хорошо работающие на ранних стадиях спирального сближения) и численное моделирование на суперкомпьютерах (необходимое при расчетах поздних этапов сближения и собственно столкновения двух черных дыр). Нейтронные звезды выводят проблему на новый уровень сложности: для этого случая требуется также решать уравнения, описывающие динамику вещества, из которого состоят нейтронные звезды. Фактически, как уже было сказано в главе 5, мы не обладаем подробной информацией о свойствах ядерного вещества при исключительно высокой плотности, по всей видимости, существующей в нейтронных звездах. Можно построить шаблоны, количественно выражающие неопределенность наших знаний о сверхплотном ядерном веществе, и тогда есть обоснованные надежды на то, что наблюдения гравитационных волн, порождаемых слияниями нейтронных звезд или столкновениями черных дыр с нейтронными звездами, дадут нам много новых сведений о свойствах вещества при крайне высокой его плотности.

Второй вопрос, возникающий в связи с шаблонами, значительно более трудный. Как мы собираемся наблюдать гравитационно-волновые события, которых не предвидели и поэтому не построили для них шаблонов? Есть и другой вопрос, связанный с первым и столь же тревожный: что, если наши теоретические модели предсказываемых событий не вполне верны? Тогда на первый взгляд может показаться, что LIGO – измерительное устройство, отягощенное систематическими ошибками и, возможно, неспособное обнаруживать полностью новые и непредвиденные события. Однако на деле все обстоит вовсе не так ужасно: ведь LIGO использует и методы анализа, не связанные с применением шаблонов, благодаря чему может заметить достаточно «громкую» гравитационную волну, даже если ее форма не соответствует ни одному из шаблонов, хранящихся в базе данных. Подобным же образом, если вследствие неправильностей шаблона проходящая через детектор гравитационная волна лишь частично совпадает с ним по форме, свободный от применения шаблонов анализ при сравнении с шаблоном тут же приведет к появлению так называемых невязок: сигналов, остающихся после вычитания оптимальной версии шаблона, вычисленной по расхождениям с чистым шумом. Проще говоря, шаблоны позволяют нам «слышать» более удаленные события, чем те, которые можно было бы регистрировать без них, и сопоставлять эти сигналы с предсказанными источниками, но они не исключают возможности, что LIGO зарегистрирует аномальный гравитационно-волновой сигнал, чье таинственное происхождение еще потребуется выяснить.

Мы закончим эту главу обсуждением численного моделирования сталкивающихся черных дыр. Такие модели являются ключевым ингредиентом для создания используемых в детекторе LIGO шаблонов. Надо подчеркнуть, что использование численных методов для решения уравнений часто является последним средством, к которому мы прибегаем, когда все аналитические вычисления на бумаге оказались не способны дать адекватное физическое описание явления. Но вспомним, что мы ограничили наше рассмотрение простым случаем столкновений черных дыр в отсутствие вещества, так что уравнения, которые требуется решить, – это знакомые эйнштейновские уравнения поля в вакууме G_µν = 0. Откуда же здесь взяться трудностям?

Они в том, что полевые уравнения Эйнштейна являются дифференциальными уравнениями, а это значит, что они локальны: метрика изменяется в пределах бесконечно малой области в пространстве и времени. Дифференциальные уравнения почти всегда трудны для решения; невероятное количество исследований в различных областях математики, физики, химии и технических наук посвящено методам поиска приближенных решений таких уравнений. Взглянем на это вот с какой стороны: компьютер можно запрограммировать так, что он будет складывать, вычитать, умножать и делить, и эти основные арифметические операции он умеет делать с поразительной быстротой. Но верное решение дифференциального уравнения включает в себя в принципе бесконечно много основных операций, потому что в результате мы получаем не просто число, но некоторую непрерывную кривую – или, в случае уравнений Эйнштейна, – искривленное пространство-время, – а это требует определения бесконечно большого количества чисел. И конечно, ни один компьютер не может выполнить бесконечное количество вычислений за конечное время. Поэтому надо стремиться не к этому, а к отысканию некоторой стратегии выполнения хотя и большого, но конечного объема вычислений, в результате которых мы, тем не менее, получили бы результат, очень близкий к точному решению наших дифференциальных уравнений. Точнее говоря, мы хотим получить стратегию построения последовательности приближенных численных решений, каждое из которых дает все лучшее приближение к точному решению наших дифференциальных уравнений. И мы не считаем численную задачу решенной до тех пор, пока не убедимся, что приближенные численные решения настолько близки к точному решению, насколько нам это требуется, при наличии достаточного времени работы компьютера. В качестве аналогии представьте себе, что вы смотрите видео при медленном интернет-соединении. Если у вас хороший браузер, вы увидите размытое, пятнистое изображение, которое, впрочем, демонстрируется с нормальной скоростью, более или менее правильной цветопередачей и не очень искаженными масштабами. Но если соединение станет работать быстрее или если, прежде чем начинать просмотр, вы немного подождете, пока большая часть видео загрузится, компьютер сможет разбить фрагменты каждого изображения на блоки меньшего размера, в результате чего в изображении будет видно больше подробностей и цвета станут менее размытыми. А если вы дождетесь загрузки всего видео или если соединение будет работать еще быстрее, вы увидите ваше видео с максимально возможном разрешением, которое допускает ваш компьютер. Примерно так же обстоит дело и с последовательными аппроксимациями численных решений дифференциальных уравнений, с той разницей, что, в принципе, вы можете улучшать ваше решение бесконечно. Единственным ограничением будет время работы компьютера, которое вы хотите или можете потратить. Говоря о численном «моделировании» уравнений Эйнштейна, мы рискуем впасть в заблуждение, будто это выражение подразумевает, что наша цель состоит в имитации существенных свойств искривленного пространства-времени при игнорировании каких-то подробностей. В действительности же нашей целью является выработка стратегии поиска именно всех деталей структуры пространства-времени с любой предустановленной точностью за конечное время. При численном моделировании сталкивающихся черных дыр дополнительным признаком успеха служит достижение хорошего согласования ваших результатов с приближенным описанием режимов спирального сближения и затухания, которое существовало до того, как были разработаны действующие современные численные методы.

Какую же стратегию следует нам применять для численного моделирования эйнштейновских уравнений поля в вакууме? Подумаем, каким бы мог быть ответ на этот вопрос. Мы хотим найти численное представление метрики, описывающей геометрию пространства-времени. Вспомним, что метрика – это правило определения расстояния между любыми двумя точками. Дифференциальная геометрия позволяет нам сосредоточить внимание только на соседних точках. Так называемый метрический тензор описывает расстояние от данной точки до любой другой, достаточно близкой к ней. В практическом смысле метрический тензор – это матрица чисел размерностью 4 × 4. Получить точное решение уравнений поля означает иметь точное значение метрического тензора в каждой точке пространства-времени. Решения Шварцшильда и Керра для черной дыры обеспечивают эту информацию в виде очень сложных математических формул. В численных моделях точных формул нет, и, разумеется, мы не можем определить метрический тензор в бесконечно большом количестве точек пространства-времени. Поэтому мы делаем так: изолируем ту область пространства-времени, которая нас в первую очередь интересует (скажем, некоторую область вокруг пары черных дыр, которые вот-вот сольются) и заполняем ее сетью точек. Каждой из конечного числа точек этой сети мы хотим приписать приблизительное значение метрического тензора. Если вернуться к аналогии с медленно загружающимся видео, нашей целью является всё большее и большее измельчение сети точек на экране, и с каждым циклом улучшения мы хотим устанавливать всё более и более точные значения всех компонентов изображения (в нашем случае – метрики) в каждой точке сети. Коротко говоря, мы дискретизируем искривленное пространство-время, чтобы свести его к математической конструкции, с которой может работать компьютер. И суть нашей стратегии численного моделирования в том, чтобы эта дискретизация происходила со всё большим и большим пространственным разрешением сети на всё большем и большем числе точек. Сегодня в типичной масштабной задаче численного моделирования задействованы сотни миллионов или даже миллиарды точек сети.

Наложить ограничения на уравнения Эйнштейна в вакууме означает, что пространство-время не может искривляться любым способом, но только в соответствии с определенными условиями, которые определяют, как именно растягивается и сжимается метрика в соседних точках пространства. Исходные уравнения Эйнштейна – это дифференциальные уравнения, а это значит, что «соседние» следует понимать как «сколь угодно близкие». Когда мы имеем дело с дискретизированным пространством-временем, приходится немного изменять уравнения Эйнштейна так, чтобы они стали теми правилами, по которым метрика в данной точке растягивает и сжимает метрику в соседних точках сети. Эти дискретизированные уравнения Эйнштейна могут, по крайней мере в принципе, быть введены в компьютер, потому что их система состоит из конечного числа уравнений с конечным числом переменных.

Остаются, правда, две трудности, которые выглядят необычно для общей теории относительности: сингулярности и ограничения. Проблема сингулярностей, вообще говоря, нам знакома и является вполне физической: в недрах черных дыр спрятаны сингулярности, в которых эйнштейновские уравнения поля теряют смысл. Если мы не проявим осторожности, численные модели пространства-времени могут распространиться и на внутренние области черных дыр, и, когда компьютер встретится с сингулярностью, возникнут проблемы. Может показаться, что это мелочь: физическая интуиция подсказывает нам, что любые проблемы, с которыми компьютерная модель встречается внутри горизонта черной дыры, можно проигнорировать, так как никакие сигналы все равно не могут появиться оттуда и «испортить» остальную часть моделирования. Но в действительности этот вопрос более тонкий, чем кажется. Если в какой-то точке некоторого слоя вычислительной сети встретилась сингулярность, – а это значит, что метрический тензор содержит некоторые бесконечные компоненты, – тогда растяжения-сжатия, закодированные в дискретизированных уравнениях Эйнштейна, сделают сингулярными и соседние точки в других слоях. Те «заразят» сингулярностью своих соседей и т. д. Очень трудно, оказывается, написать программу, которая предотвращает неконтролируемое распространение сингулярности. Правильный подход заключается в том, чтобы идентифицировать горизонт вскоре после его формирования и запрограммировать компьютер так, чтобы он не позволял модели заглядывать под него слишком глубоко. Фиксируя внутри горизонта тонкий слой пространства-времени, мы можем добиться того, чтобы вблизи горизонта физика классической теории относительности правильно отображалась дискретизированными уравнениями Эйнштейна; но исключая из рассмотрения глубокие внутренние слои, мы тем самым удерживаем компьютер от встречи с сингулярностью. В этой стратегии исключения усиленно используется принцип космической цензуры Пенроуза, согласно которому сингулярность в решениях уравнений Эйнштейна не может появиться нигде, кроме как внутри горизонта событий. И тот факт, что численное моделирование уравнений Эйнштейна успешно работает, когда мы применяем стратегию исключения в том виде, как мы ее только что описали, дает впечатляющее подтверждение принципа космической цензуры.

Проблема ограничений сама по себе более технического свойства, но ее тоже стоит упомянуть, потому что ее анализ позволяет лучше понять, как в действительности строится численное моделирование уравнений Эйнштейна. Обычно мы начинаем с некоторой исходной геометрии, например с двух невращающихся черных дыр, движущихся по орбитам друг вокруг друга, и ставим вопрос: что произойдет, когда мы отправимся вперед по оси времени? На практике это означает, что мы рассматриваем нашу большую сеть, дискрети-зирующую четырехмерное пространство-время, как разделенную на трехмерные пространственные элементы и что мы определяем течение времени в терминах функции хода, чтобы соединить эти элементы воедино. Обычно для каждого такого трехмерного пространственного элемента употребляется термин «квант времени», так как мы думаем о нем как о множестве точек в определенный момент времени. Что мы теперь должны сделать, так это задать нашему компьютеру метрику всего на нескольких (может быть, только на двух) последовательных квантах времени и затем запрограммировать его на продвижение на следующий квант посредством дискретизированных уравнений Эйнштейна. Мы планируем повторять эту процедуру, применяя стратегию исключения, чтобы избежать сингулярности, столько, сколько нам понадобится для того, чтобы черные дыры в нашей модели слились. И мы рассчитываем на то, что геометрия будет эволюционировать до тех пор, пока на последнем кванте времени в нашей модели мы не увидим единую слившуюся черную дыру плюс моментальную картину всех гравитационных волн, порожденных столкновением и уносящихся от его центра.

Но тут-то нас и ждет подвох. Как только выбор кванта времени сделан, оказывается, что некоторые из уравнений Эйнштейна не могут нам помочь в продвижении от одного кванта к следующему. Вместо этого их хватает всего лишь на то, чтобы ограничить тип геометрии, разрешенный для каждого кванта. Даже если мы сумеем со всей осторожностью добиться идеального удовлетворения этих ограничений для одного кванта времени, мы обычно обнаруживаем, что при использовании дискретизированных уравнений Эйнштейна для развития модели по оси времени ограничения для следующего кванта времени выполняются уже неидеально. Что еще хуже, это несовершенство растет со временем, и вся наша модель полностью теряет смысл! Решение этой проблемы оказывается столь же изощренным, как и сама проблема. Вместо того чтобы пытаться идеально удовлетворить ограничения на каждом кванте времени, мы должны заранее предвидеть, что в точности добиться этого не удастся – но зато мы можем изменить дискретизированные уравнения Эйнштейна, добавляя к ним то, что можно условно охарактеризовать как возвращающую силу. Она каждый раз будет как бы подталкивать решение обратно к удовлетворению ограничений. Эта возвращающая сила действует очень похоже на возвращающую силу пружины: растяните пружину от состояния равновесия, и она сожмется опять, чтобы вернуться в равновесное состояние, причем сила эта будет тем больше, чем дальше мы отошли от равновесия. В уравнения Эйнштейна мы, конечно, не вводим никакой физической силы – это скорее математический трюк, и в этом случае «равновесию» соответствует решение, удовлетворяющее ограничениям. В результате такого подхода работа с ограничениями, наряду с тщательным отбором вариантов представления уравнений Эйнштейна в дискретизированном пространстве-времени, приводит к созданию моделей, которые вполне способны отразить все детали структуры пространства-времени, проявляющиеся при столкновениях черных дыр, – конечно, при условии, что мы рассматриваем только геометрию вне горизонта.

Подведем итоги. Большинство столкновений черных дыр во Вселенной, вероятно, происходят по сценарию сближения по спирали с последующим слиянием. Этот сценарий хорошо описывается численным моделированием эйнштейновских уравнений поля в вакууме G_µν = 0. Проводя такое моделирование для широкого набора начальных условий, мы можем понять, какого рода гравитационное излучение порождают черные дыры при слиянии. В этих процессах высвобождение энергии происходит поразительно быстро – настолько, что гравитационная светимость сливающихся черных дыр может на короткое время превзойти общую усредненную светимость всех звезд Вселенной, вместе взятых. Но светимость звезд относится к оптическому диапазону, гравитационная же светимость проявляется в гравитационном излучении, которое распространяется во все стороны от сливающихся черных дыр и может быть зарегистрировано L-образными детекторами гравитационных волн, такими как LIGO. Мы надеемся, что в будущем сможем извлечь из гравитационных волн столько же информации о свойствах Вселенной, сколько мы извлекли из видимого света. Следующим большим открытием может стать регистрация гравитационных волн от сливающихся нейтронных звезд. И если удастся принять гравитационные волны из очень ранней Вселенной, они смогут нам рассказать многое о том, какой была Вселенная на заре своего существования. Лучшим подарком было бы открытие гравитационных волн такого типа, который никто не предсказывал! Тогда теоретикам пришлось бы разобраться, какие экзотические физические процессы могли их породить.