Глава 3
Шварцшильдовская черная дыра

Теперь, когда мы овладели основными положениями специальной и общей теории относительности, мы готовы начать разговор о черных дырах. Начнем его с черной дыры Шварцшильда. Если говорить совсем кратко, то шварцшильдовская черная дыра – это описание ответа пространства-времени на присутствие точечной массы. Используя выражение «ответ», мы тем самым возвращаемся к идее о том, что вещество управляет искривлением пространства-времени и что оно делает это посредством уравнений поля Эйнштейна G_µν = 8πG_NT_µν/c⁴. Искривленное пространство-время математически описывается десятью функциями метрического тензора. Уравнения Эйнштейна говорят о том, что ни один прежний набор этих десяти функций нас не устроит; требуются функции, меняющиеся в пространстве и времени единственно возможным образом, а именно образующие решение уравнений поля. Немецкий астроном и физик Карл Шварцшильд нашел такое решение. Он опубликовал свою знаменитую работу в 1916 году, хотя из его письма Эйнштейну, написанного в декабре 1915 года, ясно, что в это время, то есть очень скоро после того, как Эйнштейн полностью сформулировал свои уравнения поля, решение уже было им найдено.

Понять решение Шварцшильда оказалось очень трудно. Даже Эйнштейну, по-видимому, остались непонятны некоторые из его основных моментов, в частности гладкость горизонта. Что же представляет собой эта черная жемчужина теории тяготения, которая упала Шварцшильду прямо в руки, но которую даже Эйнштейн не смог полностью оценить?

Прошло около 50 лет после того, как Шварцшильд нашел свое решение, прежде чем физическое значение его открытия начало проясняться. Мы уже отметили некоторые стороны новой физической картины: в частности, идею горизонта событий, из-под которого не может выйти ни один сигнал, и свойства недр черной дыры, внутри которой время направлено радиально к ее центру. Для нужд астрофизики очень важно понимать, как вычислить орбиты массивных объектов, захваченных гравитационным притяжением шварцшильдовской черной дыры, и поэтому мы посвятим значительную часть этой главы описанию таких орбит и тому, как они выглядят с точки зрения удаленного наблюдателя. Мы также приложим все силы, чтобы объяснить (при отсутствии каких-либо экспериментальных подтверждений!), что, как нам кажется, должно произойти с объектом, который падает в шварц-шильдовскую черную дыру. Наконец, мы обсудим два неожиданных следствия существования шварцшильдовских черных дыр – белые дыры и кротовые норы, которые, вероятно, не имеют отношения к черным дырам, образованным в результате гравитационного коллапса старых звезд, но, тем не менее, являются частью современного понимания решения Шварцшильда. Но прежде чем мы всем этим займемся, попробуем сначала прямо ответить на вопрос: что представляет собой метрика Шварцшильда?

Вдали от горизонта она очень близка метрике Минковского, которую мы описали в главе 1. Другими словами, вдали от масс вещества пространство-время почти плоское и наблюдатели, находящиеся в нем, могут адекватно описать свои движения, а также эффекты относительного движения, такие как замедление времени и сокращение длины, с помощью одной лишь специальной теории относительности. С приближением к горизонту начинает действовать гравитационное замедление времени, о котором мы говорили в главе 2. Как отмечалось в предисловии, на горизонте событий характер хода времени полностью меняется, но, так как это очень сложная история, мы пока ограничимся областью пространства-времени вне горизонта. Здесь замедление времени полностью описывается функцией хода, которая является одним из компонентов метрики Шварцшильда. Остальная часть метрики Шварцшильда описывает трехмерное искривленное пространство вокруг черной дыры, которое находится под действием ее тяготения. Мы можем представить эти три пространственных измерения как радиус плюс два угловых измерения. Тогда двигаться в радиальном направлении означает двигаться либо прямо вверх, от черной дыры, либо вниз, в направлении ее центра. Движение по одному из угловых измерений означает, что мы обращаемся вокруг черной дыры на одном и том же радиальном расстоянии от нее.

Может показаться немного непонятным, чтó в решении Шварцшильда означает слово «радиус», так как вы не можете аккуратно измерять расстояния от центра черной дыры: под горизонтом событий находится сингулярность, которая разрушает все, что с ней соприкасается. Правильнее будет представлять себе радиус, измеряя длину окружности, в центре которой расположена сингулярность. Эта окружность может целиком лежать вне горизонта событий, на самом горизонте или даже внутри него. Если она лежит вне горизонта, то можно представить себе мысленный эксперимент, который позволил бы нам измерить длину окружности. Для этого потребовалось бы очень много наблюдателей: назовем их Алиса, Боб, Билл, Брюс, Барни и так далее, заканчивая Бушем. У каждого из них есть ракета, на которой можно добраться до любой точки на окружности. Дадим каждому наблюдателю по лазеру, а Алисе еще и секундомер. В соответствии с нашей инструкцией, Алиса должна послать лазерный импульс одному из своих соседей (скажем, Бобу) и в тот же момент запустить секундомер. Как только Боб получит от Алисы лазерный импульс, он тут же посылает из своего лазера импульс Биллу, Билл – Брюсу, и так далее по кругу. В конце концов Буш посылает сигнал Алисе, и, получив его, она останавливает секундомер. Умножив общее время, записанное секундомером Алисы, на скорость света, мы получим длину, которую можно с полным основанием назвать длиной окружности, а ее радиус легко вычислить, разделив длину окружности на 2π.

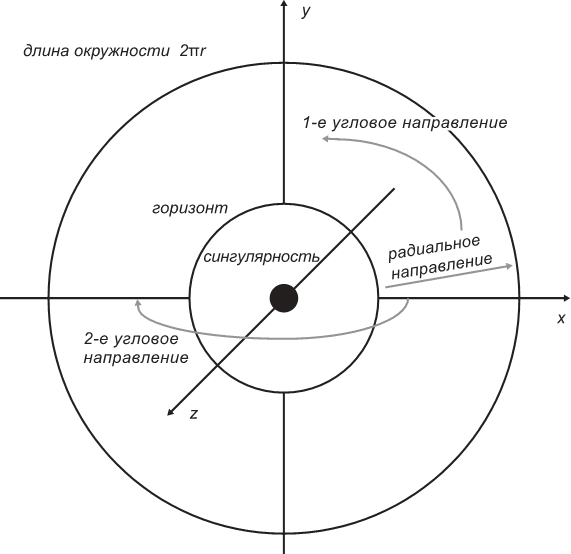
Рис. 3.1. Радиальное и угловые измерения в решении Шварцшильда.

Вне горизонта эти три направления представляют три измерения пространства. Радиус определяется так, чтобы длина окружности с центром в центре черной дыры была равна 2πr.

Определив радиус именно таким образом, мы можем теперь вернуться к явлению, которое было описано в главе 2: к тому, что пространство немного «раскрывается» в тех областях, где время замедляется. Допустим, у нас есть черная дыра, содержащая ровно одну солнечную массу, так что ее горизонт имеет радиус 3 километра. Теперь рассмотрим две окружности с центром в точке сингулярности: одну радиусом 10 километров, а другую радиусом 10 километров плюс 1 метр. Как должно быть ясно из предыдущего абзаца, когда мы говорим, что радиус первой окружности равен 10 километрам, мы имеем в виду, что ее длина равна 2π, умноженным на 10 километров; те же рассуждения можно повторить и для второй, чуть большей окружности. В плоском пространстве эти две окружности отстояли бы друг от друга ровно на 1 метр, то есть если бы вам надо было перейти с первой окружности на вторую в радиальном направлении, вам просто пришлось бы пройти 1 метр по направлению от центра. В решении Шварцшильда вам придется отойти от первого круга чуть дальше, чем на 1 метр, – примерно на 1,2 метра. Это просто голый факт. В решении Шварцшильда гравитационное красное смещение замедляет время ровно во столько же раз, во сколько растягивается радиус. Другими словами, функция хода, описывающая скорость течения времени, идеально коррелирует с другой метрической функцией, определяющей дополнительное расстояние, которое вам придется пройти в радиальном направлении от центра по сравнению с расстоянием, соответствующим плоскому пространству.

В нескольких предыдущих абзацах мы уже рассказали почти обо всех аспектах исходного решения, полученного Шварцшильдом. Осталось поговорить только об одном: о точном выражении для функции хода. Вдали от горизонта она равна единице – это означает, что время идет с той же стандартной скоростью, что и в плоском пространстве-времени. На горизонте функция хода равна нулю: обычное время здесь останавливается. Фактически это один из способов понять, что собой представляет горизонт. Между этими двумя положениями функция хода плавно меняется от нуля до единицы. Как именно это происходит? Функция хода равна квадратному корню из единицы минус некоторая постоянная, деленная на радиус. Эта формула немного трудна для произнесения, поэтому запишем ее:, где N – функция хода, r – радиус, а r_s – радиус горизонта, называемый радиусом Шварцшильда. С точностью до некоторых множителей шварцшильдовский радиус равен массе черной дыры. Все эти подробности Шварцшильд сумел извлечь из решения уравнений Эйнштейна. Неудобство решения Шварцшильда заключается в том, что функция хода на горизонте обращается в ноль, а радиальное растяжение, соответственно, становится бесконечным. В течение долгого времени считалось, что это, казалось бы, сингулярное поведение указывает на какую-то неправильность в метрике Шварцшильда. На самом деле неправильность заключается в координатах, которые мы выбрали для описания времени и радиуса: эти координаты лучше всего приспособлены для описания наблюдателей, парящих в фиксированных точках вне горизонта. Функция хода, которую мы обсуждали, тоже описывает гравитационное красное смещение именно для таких наблюдателей. То, что функция хода обращается в ноль на горизонте, просто означает, что парить, находясь на горизонте черной дыры, невозможно! Неудивительно, что метрика выглядит сингулярной с невозможной точки зрения! Вот если бы кто-нибудь описывал метрику Шварцшильда с точки зрения наблюдателя, свободно падающего в черную дыру, в положении горизонта не было бы ничего сингулярного или просто необычного. Различие между парящим и свободно падающим наблюдателями можно отразить преобразованием координат, несколько напоминающим преобразования Лоренца, но более сложным. После такой замены координат, в которых смешаны время и радиус, решение Шварцшильда на горизонте становится идеально гладким. Остается только сингулярность в центре черной дыры.

В природе решение Шварцшильда встречается нам буквально на каждом шагу. Гравитационное поле Земли можно очень хорошо приблизить простой шварцшильдовской метрикой искривленного пространства-времени. По сути дела, метрика пространства-времени в окрестности любого идеального сферического распределения масс должна точно совпадать с метрикой Шварцшильда. Отклонения от шварцшильдовской метрики на Земле (точнее, непосредственно над ее поверхностью) возникают потому, что Земля не идеально круглая, она вращается, и мы немного ощущаем гравитационное притяжение других массивных тел (в особенности Луны).

Но если мы живем в метрике Шварцшильда, не означает ли это, что горизонт черной дыры притаился где-то под нами, вблизи центра Земли? К счастью, нет! Решение Шварцшильда описывает только геометрию пространства-времени вне земной поверхности. Внутри Земли действует другое решение уравнений поля Эйнштейна, и оно не имеет никаких сингулярностей (фактически до самого центра Земли геометрия пространства-времени остается почти плоской). Так как все планеты и звезды, известные во времена, когда Шварцшильд сделал свое открытие, далеко превосходят по размерам свои шварцшильдовские радиусы, было очень заманчиво постулировать, что свойства реальной материи никогда не позволят звездам сконцентрироваться в такой маленький объем, что их радиус окажется хоть сколько-нибудь близок к шварцшильдовскому. И хотя за последующие годы было собрано много доказательств неверности этого постулата, только в 1960-х идея черных дыр по-настоящему вошла в обиход теоретической физики.

Парадоксальное свойство решения Шварцшильда состоит в том, что оно призвано описать отклик пространства-времени на присутствие в нем точечной массы, но сама эта масса не является частью уравнений, которые решаются при помощи метрики Шварцшильда. Точнее, метрика Шварцшильда является решением уравнения поля Эйнштейна в вакууме, G_µν = 0, согласно которому материи нигде нет, или, по крайней мере, ее нет вне горизонта. Внутри горизонта формулы Шварцшильда все еще работают, и по-прежнему верно, что они являются решением уравнений поля Эйнштейна в вакууме вплоть до нулевого значения радиуса. Но на нулевом радиусе метрика Шварцшильда пренеприятнейшим образом обращается в бесконечность. Причем это происходит с точки зрения любого наблюдателя. Проблема оказывается гораздо серьезнее кажущейся сингулярности на горизонте, о которой мы только что говорили. Можно было бы представить себе эту центральную сингулярность как место, в котором сосредоточена вся масса черной дыры. Но только стоит помнить, что «место» здесь будет совершенно неподходящим словом; уж лучше тогда было бы сказать «время», потому что внутри горизонта, о чем мы еще поговорим ниже более подробно, радиус есть время. Скорее всего, общая теория относительности и даже сама геометрия не способны обеспечить адекватное описание тяготения в непосредственной близости к этой центральной сингулярности. Здесь нужна какая-то другая теория, например квантовая теория тяготения или теория струн.

Подведем промежуточный итог нашего описания черных дыр. Решение Шварцшильда для уравнений поля Эйнштейна отвечает на вопрос о том, как точечная масса искривляет пространство-время: ответ – пространство-время образует черную дыру. Вдали от черной дыры пространство-время искривлено незначительно, и мы можем описать происходящее в терминах функции хода в рамках ньютоновской физики тяготения с поправкой на то, что течение времени слегка ускоряется по мере удаления от черной дыры. Но на радиусе Шварцшильда этот подход оказывается полностью неприменим: с точки зрения удаленного наблюдателя время, измеряемое наблюдателем, находящимся на горизонте событий, стоит на месте. Сначала физикам казалось, что это дефект решения Шварцшильда, а может быть, и теории Эйнштейна в целом. Но в конце концов стало понятно, что эта ситуация просто-напросто означает невозможность для наблюдателя находиться на самом горизонте. Двигаясь по радиусу вглубь, мы в конце концов приходим к сингулярности кривизны; значение этой сингулярности мы до сих пор не вполне понимаем. Наш план на оставшуюся часть этой главы таков: продолжить исследование физических свойств шварцшильдовских черных дыр, рассмотрев вопрос о том, что произойдет с наблюдателями и объектами, движущимися вокруг черных дыр или падающими в них. Мы даже поговорим о всеразрушающей области вблизи сингулярности.

Но начнем с небольшого исторического экскурса во времена, предшествовавшие открытию Шварцшильда. Эйнштейн знал об одной из самых интригующих загадок астрономии: прецессии (то есть смещении) перигелия Меркурия. Орбита Меркурия слегка эллиптична: это разрешено законами Кеплера и согласуется с ньютоновской теорией тяготения. Перигелием орбиты называется точка наибольшего ее приближения к Солнцу. Оказалось, что большая ось эллипса орбиты Меркурия, а вместе с ней и перигелий, медленно обращается (прецессирует) вокруг Солнца в том же направлении, в каком движется по своей орбите Меркурий. Эта прецессия долго и подробно изучалась, и во времена Эйнштейна уже было ясно, что она в основном может быть объяснена влиянием других планет. Загадка была в том, что даже после учета всех возможных гравитационных воздействий в рамках ньютоновского тяготения все равно оставалось расхождение между расчетами и наблюдениями, хотя и очень маленькое.

Чтобы продемонстрировать, насколько оно было мало (а заодно и насколько точными стали астрономические наблюдения в XIX веке), обратимся к числам. Орбита Меркурия прецессирует всего чуть больше чем на 574″ (угловые секунды) в столетие, а ньютоновская механика дает примерно 531″. Расхождение, таким образом, составляет 43″ за 100 лет. За один оборот Меркурия по орбите это соответствует смещению большой оси эллипса орбиты примерно на 1/35 000°. И еще до того, как Шварцшильд нашел свое точное решение уравнений поля Эйнштейна, сам Эйнштейн сумел получить достаточно хорошее приближение этого решения, которое позволило точно рассчитать движения планет в гравитационном поле Солнца. Для орбиты Меркурия эти расчеты в точности совпали со знаменитой аномальной процессией! Эврика!

На пути к окончательному виду уравнений поля, который он вывел в 1915 году, у Эйнштейна было много озарений, были и ошибки. Но это стало настоящим моментом истины. Эйнштейн понял, что он действительно создал верную релятивистскую теорию тяготения.

Теперь, когда у нас есть точное выражение для шварцшильдовской метрики, мы можем рассчитать всевозможные орбиты движения массивных тел вокруг черных дыр, орбиты, которые дают значительно более сильные отличия от ньютоновских эллипсов, чем исчезающе малая прецессия, наблюдаемая у орбиты Меркурия. И все же именно в ранних вычислениях Эйнштейна содержится зерно основной идеи, которая позволяет описать многие из этих орбит. Оставим позади Солнечную систему и направимся к центру Млечного Пути, где притаилась циклопическая черная дыра, монстр, в котором аккумулировано около 4 миллионов солнечных масс. Это не совсем шварцшильдовская черная дыра: это вращающаяся черная дыра Керра, значительно более сложный объект, который мы опишем в главе 4. Но для целей нынешнего рассказа допустим некоторую вольность и будем считать монстра в центре Млечного Пути черной дырой Шварцшильда, а заодно проигнорируем все вещество, которое может оказаться в ее окрестностях. Ее радиус Шварцшильда примерно равен 12 миллионов километров. Наши храбрые наблюдатели, Алиса и Боб, решили запарковать свой звездолет на круговой орбите радиусом 150 миллионов километров от черной дыры – это, как известно, радиус орбиты Земли, по которой она обращается вокруг Солнца. Но так как притяжение черной дыры намного сильнее притяжения Солнца (примерно в 4 миллионов раз!), то по своей круговой орбите Алиса и Боб будут двигаться гораздо быстрее, чем Земля, которая на свой оборот вокруг Солнца тратит год. Полный оборот по орбите у Алисы и Боба займет примерно 4 часа. На этой орбите гравитационное замедление времени заставит их часы идти на 4 % медленнее, чем они идут у очень далекого наблюдателя.

У Алисы на борту есть маленький космический челнок. Она собирается отчалить в нем от своего звездолета, уменьшить немного скорость своего кругового движения, тормозя двигателем челнока, а потом выключить двигатель и перейти в свободный полет. Боб обещает ей оставаться в своем звездолете и понаблюдать за ней. Чтобы помочь Бобу в его наблюдениях, Алиса прикрепляет к своему челноку ярко-желтую мигалку, которая вспыхивает раз в секунду.

По замыслу их эксперимента, как только тормозной двигатель челнока Алисы будет выключен, она начнет двигаться по геодезической в рамках геометрии шварцшильдовской черной дыры. Раз ее начальная скорость будет меньше, чем скорость ее звездолета на круговой орбите, челнок перейдет на новую орбиту, которая, конечно, будет несколько ближе к черной дыре. Если Алиса будет держать тормозной двигатель челнока включенным до полной остановки своего обращения, то она спикирует на черную дыру в радиальном направлении и будет проглочена горизонтом событий. Алиса, конечно, девушка безбашенная, но все же такой сценарий ей не нравится: она собирается сохранить определенную угловую скорость, которая позволила бы ей в этом падении лихо промчаться мимо черной дыры, обогнуть ее и снова попасть на первоначальную орбиту. Оказавшись там, она может вернуться на свой корабль или снова и снова повторять тот же головокружительный трюк с торможением.

Но вот что она должна иметь в виду: орбита ее челнока будет очень сильно прецессировать, и чем глубже в направлении черной дыры она нырнет, тем сильнее будет прецессия. Даже при небольшой эллиптичности прецессия ее орбиты будет гораздо больше, чем у орбиты Меркурия при его обращении вокруг Солнца, так как в абсолютных единицах тяготение черной дыры, у которой находятся Алиса и Боб, гораздо сильнее, чем где бы то ни было в Солнечной системе. Но, несмотря на это отличие, эффекты прецессии, которые могут наблюдать Алиса и Боб, описываются вычислениями, очень похожими на те, что проделал Эйнштейн для объяснения особенностей орбиты Меркурия.

Поэкспериментировав с разными орбитами, Алиса наконец обнаруживает, что может заставить свою орбиту прецессировать настолько, насколько захочет. Вот как она это сделает: отчалив от своего звездолета, будет осторожно регулировать начальную скорость так, чтобы нырнуть вниз до минимального радиуса, чуть большего, чем удвоенный радиус Шварцшильда, а потом заглушит двигатель. Тогда, если только Алиса верно подберет начальную скорость, она спикирует вниз, много-много раз обернется вокруг черной дыры, а потом пробкой вылетит обратно на радиус, с которого начала падение. Для движения такого типа существует специальный термин: эллипсо-вихревая орбита. Алиса чувствует себя на таких орбитах как на крутейших американских горках: все начинается со свободного падения, а в вихревой фазе движешься довольно быстро – со скоростью около двух третьих световой. Беда в том, что эта игра для Алисы весьма опасна. Если ее начальная скорость окажется чуть-чуть меньше, так что орбита занесет ее под двойной радиус Шварцшильда, она начнет падать в черную дыру и спасти ее сможет только аварийный запуск двигателей челнока, которые вынесут челнок наружу. Но при этом двигатели должны быть запущены прежде, чем Алиса достигнет горизонта, – иначе все пропало.

Рис. 3.2. Круговая орбита (сплошная кривая) и отрезок релятивистски прецессирующей эллиптической орбиты (пунктир). Нерелятивистская ньютоновская орбита (на рисунке не показана) выглядела бы как эллипс, находящийся на одном и том же месте; релятивистская прецессия заставляет этот эллипс постоянно перемещаться, как показано на рисунке.

После нескольких головокружительных полетов по эллипсо-вихревой орбите с большой высоты Алиса решает попробовать заманить Боба на орбиту пониже и поближе к себе, чтобы и он попробовал этот аттракцион. Но Боб – парень консервативный, он предпочитает не включать двигатели своего звездолета и оставаться только на круговых орбитах. Тут Алиса замечает странную вещь: чем ниже спускается Боб, тем дальше от черной дыры ей приходится оставаться на конце своей «пращи», не переходя в падение (что требует и включения аварийных двигателей).

В конце концов, когда Боб достигает радиуса, равного тройному радиусу Шварцшильда, Алисина игра с черной дырой – закружиться вокруг нее и выпрыгнуть обратно – совсем перестает получаться. Даже если ее начальная скорость оказывается лишь чуть-чуть меньше, чем у Боба, Алису затягивает в гравитационный колодец и ей приходится тут же вырываться из него с помощью аварийных двигателей, чтобы не быть проглоченной горизонтом. Боб теперь находится на так называемой предельной устойчивой круговой орбите вокруг черной дыры. Существуют круговые орбиты и с меньшими радиусами, но все они неустойчивы, а это означает, что малейшее возмущение может заставить находящегося на этой орбите нырнуть в черную дыру. Боб, естественно, на них переходить отказывается. А ведь это как раз те самые орбиты, по которым Алиса стремительно проносилась мимо черной дыры в свободном падении во время своих вихревых полетов.

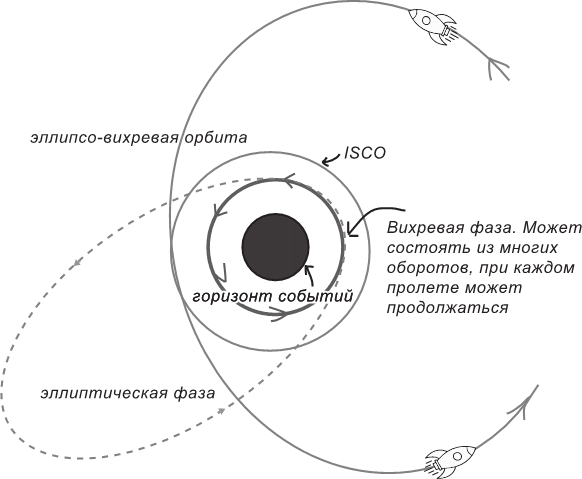
Рис. 3.3. Эллипсо-вихревая орбита.

Аббревиатурой ISCO (innermost stable circular orbit) обозначена предельная устойчивая круговая орбита.

Теперь давайте посмотрим, какие сигналы видит Боб, наблюдая за орбитальными акробатическими трюками Алисы. Не забудем, что у нее есть специальная желтая мигалка! Но сначала остановимся на минутку и поговорим об эффекте доплеровского сдвига, который наблюдается даже в отсутствие тяготения. По сути, для его объяснения не нужна и специальная теория относительности. Например, когда вы слышите сирену приближающейся машины скорой помощи, то в момент, когда она проезжает мимо вас, вы замечаете, что тон звука изменился. Для простоты представьте, что у сирены вполне определенный тон, например ля первой октавы, то есть 440 герц, 440 звуковых колебаний в секунду, и что автомобиль мчится со скоростью в одну десятую скорости звука (это довольно быстро, но возможно: примерно 120 километров в час). Когда «скорая» едет по направлению к вам, тон ее сирены примерно на 10 % выше, чем 440 герц, а когда она проехала мимо и удаляется, примерно на столько же ниже. Вот это изменение тона и есть эффект Доплера. Объясняется он тем, что когда «скорая» приближается, каждое последовательное звуковое колебание рождается чуть ближе к вам, чем предыдущее. Поэтому для вас частота колебаний становится немного больше, когда их источник приближается, чем когда он неподвижен. Похожий эффект происходит и со светом в специальной теории относительности. Если при отсутствии гравитационного поля Алиса летит прямо к Бобу, электромагнитные колебания, из которых состоит желтый свет ее мигалки, покажутся ему имеющими чуть большую частоту – или более короткую длину волны. А это значит, что желтый свет будет видеться ему скорее голубым. Соответственно, когда Алиса летит от Боба, желтые лучи ее мигалки для него будут выглядеть красноватыми. По той же причине вспышки, которые посылает ему мигалка Алисы каждую секунду (по ее часам), Боб будет принимать чаще, чем раз в секунду, когда Алиса летит к нему, и реже – когда от него. Тут может прийти мысль, что в специальной теории относительности эффект Доплера должен как-то объединяться с замедлением времени – что и происходит в действительности, и мы как раз это подробно описали.

Когда Алиса носится туда-сюда по своей вихревой орбите, гравитационное замедление времени приводит к такому покраснению света, приходящего к Бобу от ее челнока, которое выходит за рамки доплеровского. Наоборот, если бы Боб захотел послать световой сигнал Алисе, гравитация заставила бы этот свет поголубеть.

Эти гравитационные эффекты полностью объясняются переменной скоростью течения времени на разных глубинах гравитационного колодца; они имеют прямое отношение к физическим закономерностям, проявившимся в описанном в главе 2 эксперименте Паунда−Ребки. Дополнительную сложность вносит то, что фотоны светового сигнала Алисы могут добираться к Бобу по довольно сложным траекториям. Самый простой сценарий в этом случае осуществляется, когда в момент вспышки мигалки Алиса находится непосредственно под Бобом, ровно посредине своего стремительного оборота вокруг черной дыры. Тогда Боба достигнут несколько покрасневшие из-за влияния гравитации фотоны, двигавшиеся по более или менее прямолинейным траекториям вверх. Однако если в момент вспышки мигалки Алиса окажется с противоположной от Боба стороны черной дыры, фотоны хоть и все равно смогут добраться до него, но по дороге им сначала придется увернуться от черной дыры, обогнув ее! Как ни удивительно, это вполне реально, и Эйнштейн даже предвидел такую возможность. Регистрация отклонения звездного света под влиянием притяжения Солнца во время полного солнечного затмения 1919 года стала еще одним из первых экспериментальных подтверждений теории относительности, принесшим Эйнштейну мировую славу. Это отклонение не что иное, как более слабый вариант того механизма, который позволяет фотонам мигалки Алисы пробраться к Бобу с обратной стороны черной дыры вокруг ее горизонта. Но фотоны способны не только на это! Как и сама Алиса, фотоны, вылетевшие из ее мигалки, находят особую орбиту, по которой они совершают полный оборот вокруг горизонта, и даже не один, а несколько, прежде чем находят свой путь наверх, к Бобу. В принципе, фотоны могут бесконечно кружиться вокруг черной дыры на расстоянии в полтора шварцшильдовских радиуса. Эта круговая орбита, называемая световым кольцом, неустойчива, тем не менее именно из-за этого свойства черной дыры ее «тень», которую сейчас ищут, используя радиотелескопы (об этом будет коротко рассказано в конце главы 5), должна быть окружена ярким кольцеобразным ободком.

Итак, Боб увидит каждый сигнал мигалки Алисы, испытавший суммарное воздействие красного гравитационного и красного или голубого доплеровского смещений. Больше того, он увидит и слабое эхо каждого сигнала, соответствующего однократному или даже многократному обращению светового импульса вокруг черной дыры перед тем, как уйти от нее наружу. Максимальное красное смещение будет достаточным для того, чтобы фотоны перешли из видимого диапазона спектра далеко в инфракрасную область, а максимальное голубое смещение сдвинет частоту фотонов далеко в голубую часть видимого спектра. Короче, Боб увидит все цвета радуги!

Но хватит уже летать вокруг горизонта черной дыры. Пора его пересечь. Алиса и Боб подначивают друг друга это сделать, но каждый мудро уступает дорогу другому, и наконец они оба решают запустить туда автоматический зонд. Для простоты они отступают на 150 миллионов километров назад от радиуса своей исходной круговой орбиты и, зависнув там, запускают зонд. Зонд стартует из состояния покоя и радиально ныряет прямо вниз, в черную дыру, без всяких «качелей». К зонду прикреплена Алисина мигалка, чтобы можно было за ним следить. Из-за наложения воздействий гравитации и эффекта Доплера импульсы от мигалки приходят реже, чем раз в секунду, а цвет их красный. На свободно падающем зонде идет отсчет времени: 2638 секунд до достижения ISCO от начального положения на расстоянии в 150 миллионов километров, а затем дополнительные 122 секунд до достижения горизонта событий. По прошествии этого времени – по крайней мере, если верить классической общей теории относительности – зонд тихо и без всякого шума пересечет горизонт: по сути, ничем особенным этот момент не должен быть отмечен. Однако Алиса и Боб никогда не увидят, что это произошло. Гравитационное замедление времени при приближении к горизонту становится бесконечным. Другими словами, каждый следующий импульс от мигалки будет добираться до наблюдателей все дольше и дольше, и наконец настанет момент, когда придет последний импульс, – зонд пошлет его, когда будет находиться в непосредственной близости к горизонту. Совершенно не важно, насколько коротким наблюдатели установят интервал между импульсами, – допустим, что Боб и Алиса согласно первоначальному плану запрограммировали часы на зонде так, что в соответствии с их отсчетами мигалка посылает один импульс в секунду. Допустим также, что один из импульсов испущен ровно в тот момент, когда зонд пересекает горизонт. Этот импульс никогда не будет принят Алисой и Бобом, хотя все предыдущие будут. Последний сигнал, который они приняли, пришел к ним спустя 3741 секунду после выпуска зонда, предпоследний – спустя 3686 секунд. Выходит, что, с точки зрения Алисы и Боба, секундный промежуток между импульсами мигалки к моменту прихода предпоследнего и последнего сигналов растянулся до 55 секунд. Длины волн предпоследнего и последнего импульсов тоже сместились в красную сторону, увеличившись соответственно в 40 и 79 раз, и если они в момент их испускания мигалкой были ярко-желтыми, с длиной волны 570 нанометров, то Боб и Алиса увидели их инфракрасными, с длинами волн 23 и 45 микрон.

Гравитационное замедление времени (которое мы еще называем гравитационным красным смещением) обратно пропорционально функции хода, которая на горизонте обращается в ноль, а значит, время на нем замедляется бесконечно, – это и есть один из способов понять, почему Алиса и Боб никогда не увидят импульса, посланного им с горизонта, не говоря уж о тех, что посланы после этого. Можно сказать, что внутри горизонта замедление времени становится «больше бесконечного». Но что это утверждение вообще означает? Когда свободно падающий зонд минует горизонт, с ним не произойдет ничего необычного. Но если его двигатели включатся и он попытается двигаться с ускорением в обратном направлении, ничего не получится – независимо от мощности двигателей, он не сможет даже вновь вернуться на горизонт. Более того, он не сможет даже перестать двигаться внутрь. Это роковое свойство черных дыр мы уже отмечали в предисловии. Двигаться вперед во времени означает двигаться внутрь, к центру. Нет силы, способной вытащить объект из черной дыры, так же как нет силы, способной заставить что-либо двигаться назад во времени. Поэтому как только зонд пересек уровень горизонта, фотонам, испускаемым мигалкой зонда, не остается ничего, кроме как падать к центру дыры. И когда мы говорим, что замедление времени стало «больше бесконечного», мы понимаем под этим, что время внутри черной дыры совершенно не такое, как время снаружи: оно «идет внутрь», а будущее внутри черной дыры ограничено сингулярностью.

Центростремительный ход времени внутри горизонта – настолько важная в физике черных дыр идея, что для лучшего ее понимания мы вернемся к языку дифференциальной геометрии. Вспомним, что метрика пространства-времени играет двойную роль: она задает собственное время между времениподобными разделенными событиями и собственное расстояние между пространственноподобными разделенными событиями. И существует прекрасный способ объединить обе эти роли пространственно-временной метрики в одной формуле. Для этого мы напишем формулу не для расстояния, а для квадрата расстояния между двумя близкими событиями. Если квадрат расстояния положителен, значит, эти события разделены пространственноподобно, а если он отрицателен, то они разделены времени-подобно, и то, что мы принимали за квадрат расстояния, в действительности является отрицательным квадратом собственного времени между событиями. В решении Шварцшильда, как и в любом другом решении уравнений Эйнштейна, формула для метрики (основанная на функции хода, радиальном растяжении масштабов и т. д.) в действительности представляет собой одну из этих формул для квадрата расстояния, который может приобретать положительные или отрицательные значения. Для двух событий, немного разнесенных в радиальном направлении, квадрат расстояния между ними положителен над горизонтом, но отрицателен под ним. Последний пункт является ключевым: отрицательный квадрат расстояния означает, что события разделены времениподобно. Другими словами, радиус становится времениподобным, а время – пространственноподобным. Как ни странно все это звучит, ничего особенно необычного с кривизной геометрии Шварцшильда здесь не происходит; просто обычные понятия времени и расстояния при пересечении горизонта отчасти меняются местами.

Но несмотря на это их смешение, внутри горизонта наше исходное определение радиуса в решении Шварцшильда сохраняет свою силу: даже внутри черной дыры радиус все равно остается равным длине окружности с центром в начале отсчета, деленной на 2π. Это можно выразить и по-другому: площадь сферы при любом данном радиусе в решении Шварцшильда в 4π раза больше квадрата радиуса – формула, которую учат в школе. Но внутри черной дыры ее истинное значение становится даже немного пугающим: ведь радиус здесь, как мы только что узнали, является также и временем, и поэтому сфера, о которой мы говорим, представляет собой полную протяженность пространства в двух угловых направлениях в фиксированный момент времени. Когда время идет вперед (что означает движение радиуса внутрь), сфера становится всё меньше, меньше и меньше, а потом – бабах! – и вот она, сингулярность!

Чтобы объяснить наше «бабах!» при приближении к сингулярности, надо рассказать о приливных силах. Как хорошо понимал Ньютон, океанские приливы, которые происходят у нас на Земле, – это проявление гравитационного притяжения нашей планеты Луной. Луна немного сильнее притягивает ту сторону земного шара, которая обращена к ней, чем противоположную. Это неравенство сил чуть-чуть вытягивает Землю в направлении Луны, что сказывается на форме всей Земли, но так как вода – субстанция текучая, то океаны реагируют на него заметнее, чем суша. В сумме приливные силы от Луны действуют так, как если бы они тянули к Луне ту сторону Земли, которая ближе к ней, при этом вытягивая противоположную сторону Земли в обратном направлении – от Луны. Это поначалу интуитивно кажется недоразумением: мы же знаем, что тяготение – это сила притяжения, а не отталкивания! Дело в том, что приливные силы – это результирующая, которая получается после учета усредненного гравитационного воздействия Луны на Землю. Это воздействие немного меняет орбитальное движение Земли, а приливные силы несколько растягивают ее.

Рис. 3.4. Падение зонда внутрь черной дыры: вид снаружи горизонта событий.

Рис. 3.5. Падение зонда внутрь черной дыры: вид снаружи горизонта событий.

Под горизонтом зонд вовлекается в пространственно-временной коллапс.

По мере того как «время» движется от r = r_s на горизонте событий к r = 0 в сингулярности, зонд растягивается до бесконечности в одном пространственном направлении (“t”) и сжимается до нуля в двух пространственных сферических направлениях.

Когда наш зонд проваливается сквозь горизонт (рис. 3.4 и 3.5), он, в принципе, уже испытывает некоторое воздействие приливных сил, но незначительное, – ведь черная дыра такая огромная, а зонд довольно маленький, – ну, скажем, всего метр в поперечнике. Но внутри черной дыры эта ситуация быстро меняется. Как мы уже говорили, если уж зонд оказался под горизонтом, никакое ускорение не способно помочь ему избежать сингулярности. По сути, оказывается, что если мы хотим максимизировать собственное время жизни зонда прежде, чем он найдет свой безвременный конец, то лучшее, что мы можем сделать, – не заставлять его ускоряться вообще. Пусть он продолжает двигаться по геодезической. Тогда он войдет в сингулярность примерно через 27 секунд после пересечения горизонта. Приливные силы, вызванные гравитационным притяжением черной дыры, будут быстро расти по мере того, как зонд приближается к сингулярности, и к тому моменту, когда до входа в нее останется примерно от 10 до 100 микросекунд (точная цифра зависит от того, насколько прочен металл, из которого сделан зонд), его корпус разлетится на части. Растущая мощь приливных сил разнесет обломки зонда на еще более мелкие кусочки, а потом и эти кусочки распылятся на составляющие их атомы. Но и на этом дело не кончится – вскоре приливные силы вырастут настолько, что оторвут все электроны от атомных ядер, затем разорвут и сами ядра на протоны и нейтроны, а их – на кварки и глюоны. Действительно, «бабах»! Что будет дальше, неизвестно, потому что, насколько мы знаем, кварки, глюоны и электроны – точечные неделимые объекты. Но мы точно можем сказать, что два угловых направления в трехмерном пространстве сами сжимаются все сильнее и сильнее по мере приближения к сингулярности, а третье пространственное направление, соответствующее тому, что мы раньше, вне черной дыры, называли временем, испытывает еще более радикальное растяжение. В общем, всё, включая и наш зонд, сплющивается и растягивается в бесконечно тонкую линию.

Похоже, теперь мы исследовали решение Шварцшильда от начала до рокового конца. Поистине чудесным образом оно в простой и точной форме характеризует геометрию искривленного пространства-времени, в котором мы живем, и одновременно позволяет дать приближенное описание пространства-времени в окрестностях самого массивного объекта нашей Галактики, колоссальной черной дыры в ее центре. Сама по себе шварцшильдовская черная дыра абсолютно статична; она затаилась, как паук, в центре искривленной геометрической сети. Как мы теперь знаем, объекты, пролетающие слишком близко к ее горизонту, должны изо всех сил вырываться из пут ее притяжения, а всё, что пересекает ее горизонт (по крайней мере, мы так думаем!), очень скоро «переваривается» при помощи приливных сил, превращаясь в непредставимо тонкий поток вещества, устремляющийся в сингулярность.

Но это еще не конец рассказа о решении Шварцшильда. У шварцшильдовской метрики есть и другое воплощение, в пространственно-временном смысле диаметрально противоположное черной дыре, его называют белой дырой. В ней поток времени, начинающийся в сингулярности, отталкивает пространство прочь от нее, вынося всё наружу через границу, также пропускающую только в одном направлении, только вовне. И если что-то было выброшено из белой дыры, оно уже никогда не сможет вернуться обратно. Причину, по которой белая дыра должна быть частью решения Шварцшильда, можно усмотреть из следующего кажущегося парадокса. Геодезические, которые проходят мимо сингулярности, можно назвать замкнутыми: являясь оптимальными пространственно-временными расстояниями, они никогда и нигде не начинаются и не кончаются. Когда частица или фотон движутся по геодезической, для них из любой точки траектории всегда существует путь во времени вперед или назад. Это свойство может нарушаться в одном-единственном случае: если геодезическая входит в сингулярность. Чтобы понять, что произойдет в этом случае, требуется теория квантовой гравитации. Конечно, негравитационные силы могут заставить частицу двигаться по траектории, отличной от геодезической, но в качестве другого возможного пути в пространстве-времени геодезическая всегда проходит где-то поблизости. Например, если вы сидите в кресле в вашей любимой кофейне и читаете эту книгу, вы не находитесь на геодезической: вам не дает оказаться на ней давление, которое на вас оказывают кресло и земная поверхность. Но геодезическая в этом месте все равно существует – она идет сквозь поверхность Земли к ее центру, и какая-нибудь частица или объект, не подверженные этой силе давления, такие как нейтрино, могли бы по ней двигаться.

Всё это приводит к кажущемуся парадоксу в пространстве-времени Шварцшильда. Фотон, который видят Алиса и Боб и который пришел к ним, двигаясь по радиусу наружу от запущенного ими в черную дыру зонда, после того, как он был испущен источником света на зонде, двигался по геодезической. Но эта геодезическая замкнута, и поэтому она простирается за пределы источника излучения, до самого радиуса Шварцшильда и еще дальше. Теперь представим себе, что мы обратили путь фотона во времени от точки, где его увидели Алиса и Боб. Наш обращенный фотон теперь движется вспять и в некоторый момент прошлого достигает зонда. Здесь, в точке, где он был испущен, он должен окончить свое существование. Но геодезическая, по которой двигался фотон, не кончается: она продолжается в сторону меньших радиусов всё дальше назад во времени, и в принципе, нет ничего, что помешало бы проследовать по этому пути и реальному фотону: этот путь продолжается до самого горизонта, а так как радиус Шварцшильда не является сингулярностью, то он пересекает его и продолжается до всё меньших радиусов. Мы знаем, что ничто не может покинуть черную дыру. Но это как будто можно сделать по найденной нами геодезической! Мы пришли к противоречию.

Разрешение этого кажущегося парадокса состоит в том, что найденная нами геодезическая происходит не из той части метрики Шварцшильда, которая относится к черной дыре, но из совершенно другой части пространства-времени: из белой дыры, где динамический поток пространства-времени в точности противоположен текущему в черной дыре. Внутри белой дыры, где (или, скорее, «когда») радиальная координата меньше радиуса Шварцшильда, двигаться вперед во времени означает двигаться к большим радиусам. Следовательно, вместо того чтобы быть навсегда захваченной этой областью, любое тело внутри нее выталкивается наружу без малейшего шанса вернуться обратно. Нулевой радиус внутри белой дыры – это сингулярность, но приливные силы здесь противоположны тем, которые были в черной дыре: тонкие линии расплющиваются и растягиваются, снова становясь сферами.

Где же находится эта белая дыра? Или, точнее, когда? Ответ заключается в том, что белая дыра находилась в прошлом – по сути дела, в сколь угодно далеком прошлом. В подобном же смысле черная дыра – это часть будущего, и как таковая будет существовать вечно (если не принимать во внимание квантовые эффекты). Если такое объяснение кажется запутанным, есть и другой путь: провести аналогию между белыми и черными дырами и космологией Большого взрыва. В эйнштейновской теории тяготения Большой взрыв – это сингулярность, с которой «началась» наша Вселенная. (Как и в случае с сингулярностями в черных дырах, в сингулярности Большого взрыва общая теория относительности перестает работать, и что там в действительности произошло – загадка.) Хоть мы и видим повсюду вокруг нас фотоны, оставшиеся от Большого взрыва, – они образуют космический микроволновой фон, так называемое реликтовое излучение, – мы, конечно, никогда не сможем добраться до самого Большого взрыва. Это не место, а момент времени в нашем прошлом, а сейчас нам от него осталась только расширяющаяся Вселенная. Похожим образом, допуская некоторую поэтическую вольность, мы можем сказать, что решение Шварцшильда описывает пространство-время, которое родилось в виде белой дыры и от которого останется черная. Если смотреть снаружи, то любые фотоны, порожденные белой дырой, будут выглядеть, как будто они идут из той области пространства, в которой теперь находится черная дыра. И они действительно так выглядели, но когда они стремились наружу по направлению к радиусу Шварцшильда, чтобы в конце концов его пересечь, черной дыры там еще не было, была только белая.

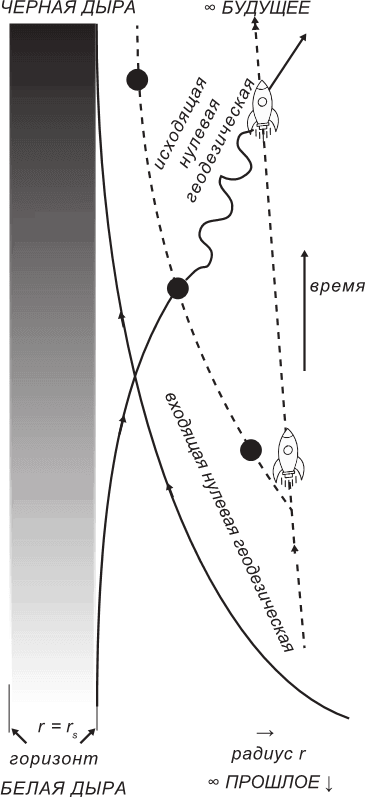
Рис. 3.6. Графическое описание природы решения Шварцшильда в форме черной/белой дыры. С точки зрения внешнего наблюдателя (в данном случае наблюдателя, находящегося в космическом челноке), все радиально исходящие нулевые геодезические происходят из белой дыры в прошлом; все радиально входящие нулевые геодезические падают в черную дыру в будущем.

Однако ни один из этих классов геодезических никогда не может быть «видим» в момент пересечения горизонта белой дыры или горизонта событий: это происходит только в бесконечном прошлом или будущем, в зависимости от наблюдателя.

Исходящий фотон, испущенный зондом, попадает на исходящую нулевую геодезическую траекторию и движется по ней до момента его поглощения (то есть наблюдения) на челноке.

Чтобы улучшить наше понимание шварцшильдовской черной дыры, мы исследовали много возможных путей движения массивных объектов (таких, как Алисин челнок или злополучный зонд) и фотонов. В совокупности все такие пути называются «причинно-следственными»: одно пространственно-временное событие может повлиять на другое, если оба они лежат на таком причинно-следственном пути, на котором первое событие предшествует второму. Если мы немного расширим наш взгляд на пространство-время и рассмотрим не причинно-следственные пути, то найдем другую замечательную особенность решения Шварцшильда: так называемую кротовую нору, или мост Эйнштейна – Розена, соединяющий внешний мир, в котором живут Алиса и Боб, с другим внешним миром, который имеет ту же самую геометрическую структуру. В этом мире подобные Алисе и Бобу авантюристы Алисия и Брэдли могли бы выполнить те же эксперименты над своей черной дырой. И они пришли бы ровно к тем же выводам, что Алиса и Боб. Однако ни одна из этих пар никогда бы не узнала о существовании другой, так как единственной связью между их мирами являются не причинно-следственные пути через внутренность либо черной, либо белой дыры, по которым не может пройти ни одна частица, массивная или безмассовая. Другими словами, две внешние области в причинно-следственном смысле отрезаны друг от друга, а внутренние области пересекаются. Считается, что кротовая нора может соединять очень далекие друг от друга части Вселенной, – эта идея породила множество научно-фантастических произведений. Беда в том, что если вы соединяете удаленные друг от друга области пространства-времени без причинно-следственной связи, то на деле это в любом практическом смысле вообще не означает никакого соединения. Если выражаться точно, не причинно-следственное соединение означает, что ничего (буквально – совсем ничего) не может перейти по этому каналу из одной области в другую. Кротовая нора непроходима. В общей теории относительности есть решения уравнений поля, описывающие проходимые кротовые норы, но все они требуют каких-то экзотических форм вещества, которые пока не открыты или, возможно, даже вообще не существуют. К обсуждению того, что может происходить в «обычных», то есть непроходимых, кротовых норах, мы вернемся в конце главы 7.

Несмотря на бурную неразбериху под горизонтом (не говоря уж о том, что может происходить в альтернативных мирах), вовне оттуда не доносится ни шороха. В сущности, это обстоятельство является проявлением одного общего свойства черных дыр, которое называют «теоремой об отсутствии волос». В этой главе мы в основном говорим лишь об одной частной категории черных дыр: о невращающихся шварцшильдовских черных дырах. В следующей главе мы рассмотрим вращающиеся черные дыры (так называемые керровские) и черные дыры, обладающие электрическим зарядом. Вы можете спросить: сколько же существует видов черных дыр? Ответ на этот вопрос такой: если вы знаете массу, заряд и спин черной дыры, то ее геометрия полностью определена. Именно это довольно сильное утверждение и называется теоремой об отсутствии волос, или, иногда, теоремой однозначности. Словом «однозначность» при этом хотят сказать, что если мы выберем некоторое конкретное значение массы, спина и заряда, то с этими параметрами будет существовать одна и только одна форма горизонта черной дыры. Термин «теорема об отсутствии волос» возник как раз из юмористического представления о том, как могли бы выглядеть неоднозначные формы горизонта, будь они возможны. Холмики, горы, ямки или долины – каким должен был бы быть общий термин для этих гипотетических особенностей рельефа горизонта черных дыр? Остановились на «волосах», и надо признать, что какая-нибудь академическая «теорема об отсутствии особенностей» запоминалась бы гораздо труднее, чем хлесткое «черные дыры не имеют волос».

Интуитивно мы понимаем эту теорему так: на горизонтах могут появляться какие-то временные особенности формы, но они сглаживаются за время, примерно равное тому, за которое свет однажды описывает вокруг черной дыры круг. Доказать это утверждение строго математически трудно. Исходная формулировка теоремы об отсутствии волос, принадлежащая канадскому физику Вернеру Израэлю, менее категорична, зато она строго доказана. Израэль доказал, что если предположить, что черная дыра стационарна (а это означает, что у нее нет временных особенностей рельефа, которые надо было бы сглаживать), то на горизонте и снаружи него невращающаяся черная дыра должна быть шварцшильдовской. Другими словами, единственной геометрией, удовлетворяющей уравнениям Эйнштейна в невращающемся стационарном пространстве-времени, является геометрия Шварцшильда. Впоследствии другие ученые распространили этот результат и на вращающиеся черные дыры, описываемые решением Керра, – мы расскажем о них в главе 4. Доказать, что стационарные решения являются единственными (что и сделал Израэль), еще не означает доказать более сильное утверждение: что все черные дыры удовлетворяют решениям Шварцшильда или Керра. Но все же Израэль сделал очень важный шаг в этом направлении.

Всё указывает на то, что решения Шварцшильда и Керра в самом деле являются устойчивыми конечными точками гравитационного коллапса. Когда черная дыра образуется в результате коллапса массивной звезды или когда две черных дыры сталкиваются друг с другом, пространство-время вблизи горизонта, разумеется, не стационарно и имеет множество интересных структурных особенностей. Но все эти структуры очень быстро уносятся прочь в виде гравитационных волн, и геометрия вне горизонта событий приобретает ту идеальную, гладкую, стационарную форму, которая описывается точным решением уравнений поля Эйнштейна. Ситуация внутри горизонта значительно менее определенная. Фактически, несмотря на принципиальное понимание решений Шварцшильда и Керра для внутренних областей черных дыр, то, что в действительности происходит внутри горизонта динамически образовавшейся черной дыры, в целом составляет тайну, которую физики и математики всё еще пытаются разгадать.

Черная дыра, возникшая в результате коллапса массивной звезды, не будет иметь в своем прошлом белой дыры – ее место занимает сама материнская звезда. Не будет там и кротовой норы, ведущей в другую вселенную. Вообще-то, всё еще выглядит таинственным и то, как появились в центрах галактик видимые там сверхмассивные черные дыры. Не исключено, что им могло предшествовать что-то похожее на белые дыры или на кротовые норы, соединяющие их с другими частями Вселенной. Но белые дыры, если они в далеком прошлом предшествовали нынешним сверхмассивным черным дырам нашей Вселенной, вероятно, должны были сильно отличаться от белых дыр шварцшильдовской метрики, так как наше наблюдаемое прошлое (Большой взрыв) довольно сильно отличается от белой дыры Шварцшильда. Также вполне правдоподобно, что сверхмассивные черные дыры образовались вследствие коллапса массивных звезд на очень ранних стадиях эволюции Вселенной, а затем постепенно увеличивались, поглощая окружающее вещество и другие черные дыры, пока не приобрели те огромные размеры, какие мы видим сегодня. В этом случае с ними не должно было быть связано ни белых дыр, ни кротовых нор. Конечный итог таков: имеется множество наблюдательных подтверждений существования в нашей Вселенной областей, содержащих черные дыры, но ни для белых дыр, ни для кротовых нор таких подтверждений нет.

Мы начали рассказывать о некоторых чудесных свойствах черных дыр, вытекающих из общей теории относительности. И теперь есть надежда, что вы понимаете, почему ученым потребовалось так много времени, чтобы прийти к общему мнению о том, что в действительности представляет собой метрика Шварцшильда – даром что она была разработана во всех математических деталях вскоре после того, как Эйнштейн опубликовал свои уравнения поля. Понадобилась большая работа математиков, в том числе получение решения Керра в 1963 году, прежде чем решение Шварцшильда стало играть столь серьезную роль. Критическое значение также имело открытие астрономами во Вселенной объектов, свойства которых не поддавались объяснению в обычных рамках, но вполне соответствовали предполагаемым свойствам черных дыр. И вновь подтвердилось, что вся общая теория относительности не просто математическая конструкция, не имеющая отношения к реальному физическому миру (каковой некоторые считали ее в первые годы после создания). К сожалению, наше современное понимание природы черных дыр выкристаллизовалось в основном уже после смерти Эйнштейна, и он не увидел, к каким поистине революционным выводам привела нас его теория.