Глава 9
Система Птолемея

Греческая астрономия нашла своего последнего значительного исследователя и учителя в лице Клавдия Птолемея Александрийского, жившего во II веке и. э. Мы почти ничего не знаем о его жизни, ни когда он родился, ни когда умер; время его жизни мы можем установить лишь по тому, что самое раннее наблюдение, о котором он говорит, что сделал его сам, приходится на 11 год Адриана (127 г. н. э.), а его последнее наблюдение – на 150 год н. э. В качестве эпохи своего звездного каталога он принимает 137 год н. э. (первый год Антонина). Как уже говорилось, его основным трудом является «Синтаксис», широко известный под названием «Альмагест», но сводка числовых данных из «Синтаксиса» (с некоторыми расхождениями) также приведена в его небольшой книге «Гипотезы планет» (к которой Прокл составил комментарий) и в надписи, посвященной «Богу Спасителю» (Птолемею Сотеру) и датируемой 10 годом Антонина.

Складывается впечатление, что за 260 лет между Гиппархом и Птолемеем астрономия не добилась никакого прогресса, если исключить труды Посидония. Единственные наблюдения, сделанные, как устанавливает Птолемей, за этот долгий промежуток времени, – это покрытие Плеяд в 92 году до н. э., наблюдавшееся Агриппой в Вифинии, и два покрытия – Спики и р Скорпиона, наблюдавшиеся Менелаем в Риме в 98 году до н. э, но, конечно, это не доказывает, что он не использовал других или, по крайней мере, что никто не вел других наблюдений в течение всего этого периода. Возможно, Птолемей больше полагался на наблюдения Менелая за неподвижными звездами, чем он сам признает. Однако в теоретической астрономии после Гиппарха не происходило абсолютно ничего, пока Птолемей не приступил к завершению своего труда и не оставил потомкам первый полный трактат, охватывающий весь спектр астрономической науки.

В начале своей первой книги Птолемей коротко резюмирует основополагающие принципы астрономии. Небеса представляют собой сферу, вращающуюся вокруг неподвижной оси, что доказывается круговым движением приполярных звезд и тем фактом, что другие звезды всегда восходят и заходят в одних и тех же точках на горизонте. Земля является шаром, расположенным в самом центре небес; если бы это было не так, то одна сторона неба казалась бы ближе к нам, чем другая, и звезды там были бы крупнее; если бы Земля находилась на небесной оси, но ближе к одному полюсу, то горизонт делил бы надвое не экватор, а один из параллельных кругов; если бы она находилась вне оси, то горизонт бы делил эклиптику на неравные части. Земля – не более чем точка в сравнении с небесами, потому что, куда бы на Земле ни отправился наблюдатель, звезды везде представляются глазу одной и той же величины и на одном и том же расстоянии друг от друга. Земля не совершает никакого поступательного движения, во-первых, потому, что должна быть некая фиксированная точка, относительно которой можно определять движения других тел, а во-вторых, потому, что тяжелые тела опускаются к центру космоса, который является центром Земли. А если бы она совершала движение, оно было бы пропорционально большой массе Земли, и потому животные и вещи оказались бы подброшены в воздух. Это также опровергает предположение, высказанное некоторыми, что Земля, будучи неподвижной в пространстве, вращается вокруг своей оси, хотя, как Птолемей признает, весьма упростило бы дело. Таким образом, в своих общих концепциях Птолемей никоим образом не отличался от своих предшественников.

Что касается движения Солнца, то Птолемей удовольствовался теорией Гиппарха. Здесь он допустил огромный промах, поскольку в течение почти трехсот лет прецессия и смещение линии апсид (о чем он не знал) увеличили ошибку в 35′, сделанную Гиппархом, примерно до 5½°. Тропический год у Гиппарха оказался слишком долгим, следовательно, среднее движение – слишком малым, и ошибка за 300 лет (с 147 г. до н. э.) дошла до 76½′, к которым еще можно прибавить максимальную погрешность 22′ в уравнении центра из-за ошибки в значении эксцентриситета, из которого исходил Гиппарх.

Таким образом, ошибка в положении Солнца в таблицах Птолемея может составить около 100′. Поистине очень странно, что Птолемей никак не попытался улучшить точность солнечной теории; возможно, она недостаточно его интересовала по причине отсутствия каких-либо неравномерностей движения, кроме одного; но, разумеется, сложность измерения абсолютной долготы Солнца с любой степенью точности не могла не стать непреодолимым препятствием на пути к вычислению более точных числовых значений солнечной теории.

Но если мы обратимся к теории Луны, окажется, что Птолемей самым существенным образом усовершенствовал работу своего предшественника. Гиппарх лишь использовал эпицикл, движущийся на концентрическом с Землей деференте. Птолемей обнаружил, что нерешенные ошибки этой теории, уже смутно замеченные Гиппархом, достигают максимума в момент квадратуры и совершенно исчезают в сизигии; однако еще одна трудность заключалась в том, что ошибка не повторяется в каждой квадратуре, порой исчезая вовсе, а порой достигая целых 2°39′ – своего максимального значения. В конце концов выяснилось, что, когда Луна оказывалась в квадратуре и в то же время в перигее или апогее эпицикла, так что уравнение центра было равно нулю, местоположение Луны прекрасно согласовывалось с теорией Гиппарха, но при этом ошибка оказывалась наибольшей всякий раз, когда уравнение центра достигало максимума в момент квадратуры. Таким образом, действие второго неравенства всегда увеличивало абсолютное значение первого, особенно в квадратурах. Из этого следовал очевидный вывод, что радиус эпицикла имеет переменную длину, большую в квадратуре, чем в сизигии. Поскольку нельзя было предположить, что изменяется длина радиуса, изменяться должно было расстояние от поверхности Земли, чтобы она могла появляться под разными углами в разное время; другими словами, центр эпицикла должен был двигаться по эксцентру, но так, чтобы угловая скорость была равномерной, и не относительно центра круга, а относительно Земли.

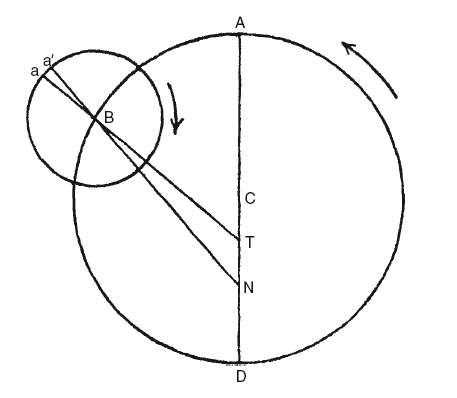
Но в то же время предполагается, что линия, проходящая через центр и апогей эксцентра, вращается в попятном направлении вокруг Земли, так что угол, который она образует с линией от Земли до центра эпицикла, угол АТВ, равнялся удвоенной элонгации Луны от Солнца, составляя 180° в первой и последней четверти. Таким образом, расстояние до В от Земли Т будет наибольшим в сизигии (фактически таким же, каким оно было бы по теории Гиппарха) и наименьшим в квадратуре. Второе неравенство происходит по причине того, что эпицикл не находится в том положении, в котором находился бы, если бы двигался по концентрическому кругу, и она равна углу между линиями, проведенными от Земли до двух местоположений Луны в соответствии с двумя теориями. Этот угол равен нулю в сизигии, так как центры эпицикла и эксцентра (В и С) находятся на одной линии с Землей и по одну сторону от нее, в то время как эпицикл лежит именно там, где должен находиться по теории Гиппарха. В квадратуре центры находятся на противоположных сторонах от Земли, и потому эпициклы, согласно двум теориям, наиболее удалены друг от друга. Если, однако, в это время Луна будет находиться в перигее или апогее эпицикла, он будет расположен на линии CD, а угол, представляющий второе неравенство, все равно будет равен нулю; в то время как наибольшего значения (2°39′) он достигнет, если линия, соединяющая Луну с В, будет находиться под прямым углом к этой линии, то есть когда аномалия Луны составит 90° или 270°. Исходя из максимального значения суммы двух неравенств 740′, с помощью простого вычисления получаем СТ: ТА = 49,7: 10,3.

Птолемей, таким образом, сделал большой шаг вперед, открыв второе неравенство, которое в наши дни называется эвекцией, и установив его величину – 1°19′30″, очень близкую к истинному значению, а также адаптировав к нему теорию Гиппарха. Однако продолжение наблюдений показало, что теория еще недостаточно разработана, так как в ней остаются нерешенные ошибки. Не смутившись этим, Птолемей снова приступил к решению проблемы, но не сумел обнаружить третье неравенство (вариацию) и лишь еще больше усложнил теорию. Аномалия, как мы видели выше, всегда отсчитывалась от линии апсид эпицикла, проходящей через Землю. Птолемей предположил, что она не проходит через Землю, но всегда направлена к точке N, расположенной на том же расстоянии от Г, что и С (ТС = TN). Среднее значение апогея, таким образом, составляет а′, в то время как видимый апогей а немного колеблется в обе стороны от положения среднего апогея, так что они совпадают в сизигиях и квадратурах. Поправку к аномалии, обусловленную таким расположением (просневсис, πρόσνευσις τοῦ ἐπικύκλου), следует применить к уравнению центра перед нахождением поправки на эвекцию.

По теории Птолемея, видимое местоположение Луны в момент сизигии и квадратуры можно определить с такой точностью, которая с практической точки зрения была достаточна для своего времени, поскольку он и его современники обладали лишь грубыми инструментами, неспособными фиксировать положение небесного тела без погрешности до 10′. Но хотя его теория таким образом оказалась почти достаточной для вычислений, она не позволяла определить фактическое местоположение Луны в пространстве, так как очень сильно преувеличивала вариацию расстояния от Луны до Земли. Опираясь на вавилонские наблюдения двух лунных затмений, происходивших вблизи апогея эпицикла, Птолемей находит видимый диаметр Луны в апогее эпицикла и эксцентра, равный 31°20″ (с превышением всего примерно на 2′). Из приведенных числовых данных нетрудно понять, что при наименьшем расстоянии от Земли диаметр Луны составит почти градус. Но хотя Птолемей не мог этого не заметить, он оставляет этот факт без внимания. Сейчас считается общепризнанным, что теория эпициклов была лишь средством для вычисления видимого положения планет и не претендовала на отображение истинной картины мира, и в этом смысле она, безусловно, достигла своей цели, причем в весьма элегантной манере с математической точки зрения. Для греческого ума теория обладала одним серьезным изъяном: в ней нарушался принцип строго равномерного движения как путем введения точки вне центра деферента, относительно которого угловое движение было равномерным, так и просневсисом. Это было совершенно непростительно с точки зрения физики, но математически, разумеется, вполне допустимо. Это был шаг к открытию эллиптического движения, но прошли многие века, прежде чем труд Птолемея был продолжен.

Человек, смогший настолько продвинуть вперед теорию Луны, естественно, не собирался оставить теории пяти других планет в том же плачевном состоянии, в котором он их нашел. Как будто чтобы еще больше подчеркнуть отличие этих светил с их гораздо более нерегулярными движениями от Солнца и Луны, он всегда говорит о них как о «пяти блуждающих звездах» (οἱ πέντε πλνώμενοι), хотя в Античности более обычным было говорить о семи планетах. Он рассматривает их движение относительно плоскости эклиптики, к которой плоскость деферента каждой планеты наклонена под определенным небольшим углом. Но деферент (в отличие от теории Аполлония) является не концентрическим с Землей, а эксцентрическим, чтобы учитывать зодиакальное неравенство, которое на самом деле вызывает эллиптическая форма орбиты. Эпицикл, на котором планета движется с равномерной скоростью, объясняет аномалию или второе неравенство (стояния и попятные движения). Радиус от центра эпицикла к планете (для Марса, Юпитера и Сатурна) параллелен линии, указывающей на среднее место Солнца, тогда как для Меркурия и Венеры центр эпицикла лежит на этой линии. Как и в системе Аполлония, периоды обращения таковы:

Но и при этом теория Аполлония оказывалась недостаточной; Птолемей счел необходимым добавить усложнение, несколько похожее на то, благодаря которому ему удалось закончить свою лунную теорию. Наибольшее расхождение между средним и наблюдаемым местоположением оказалось больше в апогее и меньше в перигее, чем это могло объяснить эксцентрическое движение, таким образом центр расстояний должен быть ближе к Земле, чем центр равномерного движения. Поэтому он ввел точку экванта, расположенную на линии апсид, таким образом мы имеем следующий порядок: земля (7) – центр деферента (С) – эквант (Е). Птолемей обнаружил, что наибольшее соответствие наблюдениям обеспечивается при ТС = СЕ. Точка Е в планетной теории не имела прямого отношения к движению на эпицикле; но линия от экванта до центра эпицикла двигалась так, что описывала равные углы за равные промежутки времени. Поэтому точка Е была центром равного движения, а С — центром равных рас– стояний. Но и этого было недостаточно для планеты Меркурий, у которого центр движения (Е) находился между Землей и центром деферента, с расстоянием от второго до первого равным ¹/₂₀ радиуса деферента, но центр деферента не стоит неподвижным, а, напротив, описывает небольшой круг с радиусом ¹/₂₁ в направлении с востока на запад вокруг точки (С), удаленной на ¹/₂₁ от Е, за тот же период, за который центр эпицикла обходит вокруг деферента.

Наклоны планетных орбит к эклиптике настолько малы, что Птолемей в своих теориях движения по долготе посчитал допустимым пренебречь отклонениями от эклиптики. Но сами широты дали ему достаточно хлопот, и он, по-видимому, нашел, что эту часть очень сложно привести в удовлетворительный порядок (кн. XIII). Для трех внешних планет он предположил, что деферент наклонен к плоскости эклиптики под углом 1° для Марса, 1°30′ для Юпитера и 2°30′ для Сатурна. Для Марса линия апсид деферента перпендикулярна линии узлов, так что она совпадает с линией, соединяющей точки наибольшей северной и южной широты; для Юпитера – 20° к западу, а для Сатурна – 50° к востоку от линии наибольшей широты. Апогеи во всех трех случаях находятся к северу от эклиптики. Но эпициклы, в свою очередь, наклонены под тем же углом к плоскости дифферентов, так что их плоскости всегда параллельны плоскости эклиптики. Птолемей пришел к этому предположению, заметив, что в апогее и перигее деферента широта (южная и северная соответственно) достигает наибольшего значения, когда планета оказывается в перигее своего эпицикла. Так как эпицикл внешней планеты является не чем иным, как годовой орбитой Земли вокруг Солнца, перенесенной на рассматриваемую планету, конечно, он был совершенно прав в том, что эпицикл должен быть параллелен плоскости эклиптики. Оставаясь таким образом параллельным некоей плоскости, эпицикл с античной точки зрения вел себя необычно, поскольку считалось естественным, что плоскость эпицикла должна находиться под тем же углом к радиусу, соединяющему центр деферента с центром эпицикла. Поэтому гипотеза требовала введения небольшого вспомогательного круга, плоскость которого была бы перпендикулярна к плоскости деферента, а центр лежал бы в плоскости последнего и который совершал бы оборот в зодиакальный период планеты (XIII, 2). Если представить себе стержень на окружности этого круга, который входит в прорезь на эпицикле, можно понять, каким образом эпицикл остается параллельным эклиптике. Это позволяет более-менее объяснить разницу наибольших широт, но, видимо, Птолемея такое совпадение не удовлетворило, так как потом он, похоже, счел необходимым изменить наклоны эпициклов соответственно на 2°15′, 2°30′ и 4°30′, причем диаметр эпицикла, перпендикулярный к линии перигея-апогея, всегда параллелен плоскости эклиптики.

Меркурий и Венера потребовали совсем иного подхода. На рисунке А — апогей, а Р — перигей деферента; NN′ – линия узлов, или линия пересечения плоскостей деферента и эклиптики. Угол между ними очень мал, 10′ для Венеры и 45′ для Меркурия, а плоскость деферента колеблется в этих пределах в обе стороны от эклиптики, совпадающей с плоскостью деферента, когда центр эпицикла приходится на N или N′. Что касается эпицикла, то его линия апсид ab падает на плоскость деферента в А и Р, тогда как диаметр cd, находящийся под прямым углом к ней, наклонен к этой плоскости под углом, который назван λόξωσις (обликвация). В узлах NN′ диаметр cd падает на плоскость эклиптики, а ab наклонен к деференту. Этот наклон эпицикла называется ἔγκλισις и равен нулю в точках А и Р. В случае Меркурия планета в апогее находится к югу от эклиптики, а Венеры (и всех других планет) – к северу от нее. Следовательно, когда эпицикл Венеры находится в N′ (восходящий узел), деферент лежит в плоскости эклиптики; по мере продвижения эпицикла точка А поднимается к северу от эклиптики и продолжает подниматься, пока эпицикл не достигнет А. После этого широта уменьшается, пока не становится равной нулю в N, но после этого часть NPN’ поднимается к северу от эклиптики, унося эпицикл с собой, так что центр последнего всегда находится на северной широте, за исключением точек N и N′. В то же время происходит двойное колебание эпицикла, как у корабля при одновременной килевой и бортовой качке. У Меркурия все наоборот относительно севера и юга, а в остальном теория такая же.

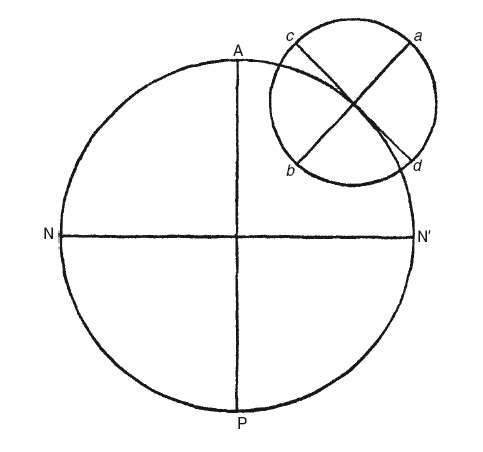
То, что Птолемей нашел широты планет крайне хлопотным делом, ничуть не странно, если вспомнить, что на самом деле их линии узлов проходят через Солнце, в то время как Птолемею пришлось исходить из допущения, что они проходят через Землю. Поскольку внутренние планеты практически окружены орбитой Земли, также вполне естественно, что их движения по широте казались более сложными. Фундаментальная ошибка системы Птолемея не вызвала столько трудностей ни в одной другой части планетной теории, как в объяснении широт, и они оставались основным камнем преткновения вплоть до эпохи Кеплера.

Невозможно отрицать, что система в целом заслуживает нашего восхищения как готовый способ составления таблиц движения Солнца, Луны и планет. С геометрической точки зрения она почти во всех подробностях (за исключением вариаций расстояния до Луны) представляла эти движения почти так же верно, как наблюдения при помощи простых инструментов того времени, и является вечным памятником великим математическим умам, разрабатывавшим ее с таким упорством. Из многих слов не только самого Птолемея, но и его комментаторов следует, что они всего лишь считали многочисленные круги удобным способом расчета местоположения планет и в действительности система весьма похожа на разложение в ряд синусов или косинусов кратных средней аномалии. Птолемей обычно начинает теорию какой-либо части планетного движения со слов «представим себе (νοείσθω)… круг», а во введении к своим «Гипотезам» он говорит: «Я не утверждаю, что могу сразу объяснить все движения; но я покажу, что каждое само по себе прекрасно объясняется своей собственной гипотезой». А Прокл в конце своего комментария открыто говорит, что эпициклы и эксцентры предназначены всего лишь для того, чтобы наиболее простым способом объяснить движения и показать существующую между ними гармонию. Факт (на который Гиппарх и Птолемей не могли не обратить внимания), что их лунная теория требует чрезмерных изменений расстояния до Луны и тем самым ее видимого диаметра, чего в действительности не происходит, показывает, что они видели в своей работе не систему действительного мироустройства, но всего лишь вспомогательное средство для вычислений. В силу состояния алгебры в ту эпоху их приходилось производить геометрически, как и Евклиду пришлось удовольствоваться геометрическим представлением в вопросах иррациональных величин или теории пропорций.

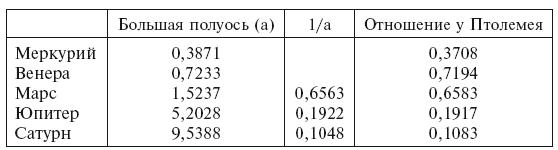
Современному уму, привыкшему к гелиоцентрической идее, трудно понять, почему такому математику, как Птолемей, не пришло в голову лишить все внешние планеты их эпициклов, раз они не служили никакой иной цели, кроме воспроизведения годовой орбиты Земли, переданной на каждую из этих планет, а также лишить Меркурий и Венеру их деферентов и поместить центры их эпициклов на Солнце, как сделал Гераклит. Фактически мы могли бы воспроизвести установленные Птолемеем значения отношений радиусов эпицикла и деферента на основе большой полуоси каждой планеты, выраженные в полуосях Земли, как показано в следующей таблице:

Очевидно, что гелиоцентрическая идея Аристарха могла с тем же успехом возникнуть из теории эпициклов, как и из теории подвижных эксцентров, и, если бы мы не располагали некоторыми данными в пользу старшинства первой из двух теорий, мы не могли бы сказать, какая из них послужила отправной точкой для Аристарха. Но в связи с любопытной зависимостью всех планет от Солнца в системе Птолемея мы уже упоминали, что зодиакальное неравенство движения планет показывает, что в любом случае простое круговое движение не может «спасти явления»; при этом открытие ярко выраженной неправильности движения Луны, зависящей от ее положения относительно Солнца, подтвердило мнение, что Солнце одинаково замешано в теориях всех небесных тел.

Хотя система Птолемея была лишь геометрическим представлением небесных движений и не претендовала на изображение истинной картины реального мироустройства, невозможно обойтись без нее в нашем обзоре космических систем, прежде всего в силу ее огромной исторической важности. В течение более чем четырнадцати столетий она оставалась альфой и омегой теоретической астрономии, и, какие бы ни складывались мнения об устройстве мира, система Птолемея почти повсеместно считалась фундаментом астрономической науки.

Помимо полной теории движения планет, великий труд Птолемея содержит и каталог звезд, который, однако, представляет собой не что иное, как каталог Гиппарха, сохранивший с его времен ошибочное значение постоянной прецессии. Гиппарх открыл прецессию равноденствий, сравнив определенные им самим долготы для некоторых звезд с их долготами у Тимохариса, определенными примерно на 150 лет раньше. Уже в своей более ранней работе о продолжительности года он заявлял, что это смещение должно составлять по меньшей мере градус на сто лет («Синтаксис», VII, 2), но в своей последующей работе «О смещении точек солнцестояния и равноденствия» он говорит, что Спика, по его наблюдениям, находится в 6° от осеннего равноденствия, тогда как у Тимохариса это расстояние составляет 8°. Тимохарис наблюдал Спику в 294 и 283 годах до н. э. (VII, 3), а Гиппарх наблюдал ее в 129 году, таким образом изменение составило 45″ или 46″ в год. Значения, принятые Гиппархом для тропического и сидерического года, также указывают на то, что он исходил из указанной величины. Птолемей, однако, сравнивая найденные Тимохарисом и Гиппархом долготы четырех звезд с теми, которые определили Агриппа и Менелай в 93 и 98 годах н. э., нашел смещение на 36″ за год, или на 1° за 100 лет, и принял это удобное и круглое число. Весьма примечательно, что такое важное открытие не стало общеизвестным и мы не находим упоминаний о прецессии ни у Гемина, ни у Клеомеда, ни у Теона Смирнского, Манилия, Плиния, Цензорина, Ахилла, Халкидия, Макробия или Марциана Капеллы! Единственные авторы, которые говорят о ней, за исключением Птолемея, – это Прокл, который категорически отрицает ее существование, и Теон Александрийский, который принимает птолемеевское значение 1° за 100 лет, но рассказывает об этом вот такую странную историю: «По мнению некоторых, древние астрологи полагали, что с некой эпохи точки солнцестояний сдвигаются на 8° по порядку знаков, после чего возвращаются на то же расстояние; но Птолемей был не такого мнения, так как без введения этого смещения в расчеты они, если делаются по таблицам, всегда согласны с наблюдаемыми местами. Поэтому мы также советуем не использовать эту поправку, но все же объясним ее. Допустим, что за 128 лет до правления Августа произошло наибольшее смещение вперед, а именно на 8°, звезды начали двигаться назад; к 128 годам, истекшим до Августа, прибавим 313 лет до Диоклетиана и 77 лет после него и возьмем одну восьмую часть от суммы (518), так как за 80 лет происходит смещение на Г. Доля (6°28′30″), вычтенная из 8°, даст величину, на которую точки солнцестояния окажутся впереди таблиц».

Единственный древний автор, который упоминает об этой теории, – это Прокл, и он всего лишь говорит, что точки тропиков, по мнению некоторых, не совершают полный круг, а движутся на несколько градусов взад-вперед («Гипотезы»).

Таким образом, по мысли этих людей, долгота звезды увеличивалась в течение 640 лет (на 1° за 80 лет), а затем вдруг стала уменьшаться и продолжала делать это в течение еще 640 лет, а затем столь же внезапно снова стала расти. Эти добрые люди, видимо, жили прежде Птолемея, так как он с ними не согласен (и так как Теон называет их παλαιοί), но при этом позже Гиппарха, так как они что-то знали о прецессии и исходили из ее значения 45″ в год. Но что навело их на эту необычную мысль? И почему они относят перемену направления к 158 году до н. э.; и почему длина дуги составляет 8°? На все эти вопросы трудно ответить. Вероятно, к этому году они относят начало астрономических трудов Гиппарха, и единственное, что связывает с Гиппархом смещение равноденствий и солнцестояний на 8°, – это то, что он наконец-то поместил начало знаков Овна, Рака, Весов (клешней Скорпиона) и Козерога в точки равноденствия и солнцестояния, как это делал Арат, тогда как Евдокс и другие помещали эти точки в середине или восьмом градусе этих знаков. При этом они следовали примеру вавилонян, у которых эклиптика была неподвижной и определялась созвездиями. Кутлер обнаружил, что равноденствие у них находилось в 8°15′ Овна, а долготы новолуния в среднем на 3°14′ больше, так что начала знаков вавилонской эклиптики соответствуют примерно пятому градусу знаков нашей подвижной эклиптики. Много лет спустя Плиний по-прежнему указывает, что восьмой градус совпадает с равноденствиями и тропиками, а Манилий (III, 676) и Ахилл (с. 23) говорят, что одни авторы помещают их в начале знаков, другие – в восьмом градусе, третьи – в десятом или двенадцатом. Возможно, некоторые невежественные авторы по недоразумению заключили из этого разночтения, что равноденствие колеблется взад-вперед, и таким образом положили начало теории об изменчивости прецессии, которая вследствие плачевного состояния или, вернее, отсутствия практической астрономии на протяжении многих веков после Птолемея упрочилась, распространилась в Индии и среди арабов и не была окончательно отметена до тех пор, пока на сцену не вышел Тихо Браге.

Птолемей не только не разделяет этой ошибки, он ни разу нигде на нее не ссылается. Для него прецессия – просто медленное вращение сферы неподвижных звезд с запада на восток вокруг полюсов зодиака, происходящее за 36 000 лет. Едва ли можно сомневаться в том, что Гиппарх был того же мнения. Правда, он назвал свой трактат не «О смещении неподвижных звезд», а «О смещении (μετάπτωσις) точек солнцестояния и равноденствия», и, по словам Птолемея («Синтаксис», VII, 2), он говорил в своей книге о продолжительности года, что тропики и равноденствия «по этой причине перемещаются к западу», но Птолемей умалчивает о том, что Гиппарх расходится с ним во мнении, и в двух других местах (III, 1 и VII, 1) четко говорит, что Гиппарх высказал гипотезу о медленном вращении сферы в том же направлении, в котором движутся планеты. Кроме того, хорошо известно, что Гиппарх сначала приписывал смещение на восток лишь нескольким зодиакальным звездам, долготы которых, как он обнаружил, увеличились, хотя вскоре он понял, что это смещение общее для всех звезд.

Птолемей был последним великим астрономом александрийской школы. За ним последовали несколько выдающихся математиков, такие как Папп и Диофант, но они ничего не прибавили к накопленным астрономическим знаниям. Труды Птолемея по-прежнему преподавали в школах; Теон Александрийский написал к ним ценный комментарий, но он, пожалуй, был последним ученым человеком, который имел возможность пользоваться прославленной библиотекой, ведь она погибла при его жизни от рук толпы разъяренных христиан города (в 389 г. н. э.). Его знаменитая дочь Гипатия, которая по праву считается олицетворением высших достижений греческой культуры и мысли, была по этой самой причине варварски растерзана несколько лет спустя (в 415 г.), и занавес навсегда опустился над грандиозной сценой, где греческая наука играла свою роль так ярко и так долго. В Греции еще была жива неоплатоническая школа и даже дала человечеству последнего выдающегося философа – Прокла, после смерти которого она еще полвека влачила жалкое существование, пока император Юстиниан не закрыл ее в 529 году. В компании с шестью другими философами Симпликий (впоследствии написавший сложный комментарий к Аристотелю, на который мы часто ссылаемся) искал убежище в Персии, пребывая в заблуждении, что они найдут там непредвзятых правителей и свободу, чтобы учить; но их ждало разочарование, они вернулись домой через несколько лет и обнаружили, что нигде в известных частях мира мудрость прошлого уже не пользуется никаким уважением. Над миром спустилась долгая, темная ночь Средних веков.