Язык — это человеческое изобретение, которое является зеркалом души. Именно посредством языка хороший роман, пьеса или стихотворение учат нас быть людьми. С другой стороны, математика — это язык природы, который служит зеркалом физического мира. Это точный, чистый, развитый и строгий язык. Несмотря на то что эти качества делают язык математики идеальным для описания явлений природы, они же делают его непригодным для отражения сугубо человеческих проблем и страданий. Так возникает центральная дилемма «двух культур».

Нравится нам это или нет, но числа являются главными действующими лицами физической драмы. Всё, что мы делаем в физике, в том числе всё, что мы думаем о физическом мире, в конечном итоге сводится к числам. Причём характер наших размышлений об этих числах полностью определяется тем, откуда они берутся. Таким образом, физики и математики думают о числах принципиально разными способами. В отличие от математиков, физики используют числа в дополнение к своей физической интуиции, а не вместо неё. Математики же занимаются абстрактными структурами, и их совершенно не волнует, могут ли придуманные ими математические объекты существовать в природе. Для математика число существует само по себе, как отдельная реальность, в то время как для физика оно, как правило, не имеет смысла в отрыве от физического мира.

Числа в физике несут на себе багаж связей с измеряемыми физическими величинами. А любой путешественник знает, что багаж имеет как плохую, так и хорошую сторону. С одной стороны, багаж тяжело тащить, его могут украсть, за него приходится дополнительно платить. С другой стороны, в багаже мы везём множество полезных вещей, необходимых нам в путешествии. С одной стороны, багаж сковывает вашу свободу передвижения, с другой — освобождает от необходимости стирать бельё каждый день. Точно так же и числа: с одной стороны, они усмиряют нашу фантазию, ограничивая её жёсткими математическими рамками, с другой — являются неотъемлемым атрибутом упрощения картины мира. Числа освобождают нас от груза несущественных деталей, показывая, что мы можем игнорировать, а что нет.

То, что я сказал, находится в прямом противоречии с преобладающим мнением, что числа и математические соотношения только усложняют понимание и их следует избегать любой ценой, даже в научно-популярных книгах. Стивен Хокинг в своей «Краткой истории времени» заявил, что каждое уравнение в популярной книге сокращает количество продаж вдвое. Выбирая между количественным и качественным объяснением какого-нибудь явления, большинство людей, вероятно, предпочтут второе. Мне представляется, что главная причина общего отвращения к математике лежит в области социологии. Математическая безграмотность в нашем обществе возводится едва ли не в достоинство — неспособность сложить пять чисел, чтобы проверить правильность счёта в ресторане, считается проявлением человечности, а не глупости. Но я считаю, что корни этого явления в том, что в начальной школе детям не показывают, что стоит за тем или иным числом, и числа представляются им не столь важными в повседневной жизни, как слова.

Я, помню, был поражён, когда несколько лет назад, читая курс физики для нефизиков в Йельском университете — храме литературной грамотности, — обнаружил, что 35% студентов, в числе которых были выпускники исторических и социологических факультетов, не могли назвать даже порядок величины населения Соединённых Штатов! Многие думали, что в США проживает от одного до десяти миллионов человек — меньше, чем в одном только Нью-Йорке.

На мой взгляд, это признак глубоких проблем в нашей национальной системе образования. И дело даже не в том, что, живя рядом с Нью-Йорком, люди не отдают себе отчёта в том, что население всей Америки не может быть меньше населения одного Нью-Йорка. И даже не в непонимании того, что страна с населением 1 миллион человек будет радикально отличаться от страны с населением 100 миллионов. Главная проблема в том, что для большинства из этих студентов такие числа, как 1 миллион или 100 миллионов не имели никакого объективного смысла. Они никогда не пытались сопоставить, например, миллион чашек кофе с количеством людей, которые их выпивают утром в миллионном городе. Многие не могли назвать мне даже приблизительно расстояние от восточного до западного побережья Соединённых Штатов — они не умели заставить свой мозг сделать простейшую прикидку: умножить расстояние, которое они проезжают за день на автомобиле (около 800 километров) на число дней (5–6 дней), которое необходимо, чтобы пересечь Американский континент, и понять, что это расстояние ближе к 4000–5000 километрам, нежели к 10 000 или к 20 000.

Размышления о числах в терминах того, что эти числа представляют, — самое захватывающее из всех занятий. Именно на этом специализируются физики. Я не возьмусь утверждать, что математические размышления доставляют чувство какого-нибудь особенного комфорта или являются магическим лекарством от математического бессилия, но играть с числами, выясняя, откуда то или иное число появилось в нашем мире и что за ним стоит, достаточно интересно, очень полезно и совсем не сложно. По крайней мере, необходимо научиться оценивать порядок физических величин, а это уже позволит делать важные выводы, не проводя точного количественного анализа. В этой главе я нарушу максиму Стивена Хокинга, очень надеясь, что не разорю своего издателя, и покажу, как физики манипулируют числами, чтобы сделать задачу более понятной, почему они делают это именно так, а не иначе, и что они ожидают получить от этого занятия. Основную идею можно сформулировать так: «мы используем числа, чтобы сделать вещи не сложнее, чем они должны быть».

Прежде всего следует отметить, что физические явления охватывают чрезвычайно широкий спектр возможных числовых значений и очень большие или очень маленькие числа могут появляться при решении даже простейших задач. Самое трудное при работе с такими числами — это подтвердит любой, кто хотя бы раз пытался перемножить столбиком два восьмизначных числа, — не запутаться в количестве цифр. К сожалению, часто самые трудные вещи являются одновременно и самыми важными, поскольку количество цифр определяет порядок числа. Допустим, мы умножаем 40 на 40. Какой ответ будет ближе к правильному: 160 или 2000? Ни одно из этих чисел не является точным значением произведения, но второе гораздо ближе к правильному ответу 1600. Если бы работодатель, пообещав платить вам по 40 долларов в час, заплатил за 40 часов работы только 160 долларов, тот факт, что он потерял всего лишь один нолик, был бы для вас слабым утешением, не правда ли?

Чтобы избежать подобных ошибок, физики придумали разделять числа на две части, одна из которых сообщает вам порядок числа, а вторая — точное значение в пределах этого порядка. Такая запись числа называется экспоненциальной. Она позволяет избежать записи огромного количества нулей, когда необходимо выразить в привычных нам единицах такие значения, как, например, размер наблюдаемой части Вселенной, составляющий около 1 000 000 000 000 000 000 000 000 000 сантиметров.

Глядя на это число, любой скажет, что оно очень велико, но насколько велико?

В экспоненциальной нотации используются степени числа 10. Запись 10ⁿ означает число, начинающееся с единицы, за которой следуют n нулей. Например, число 100 в экспоненциальной нотации записывается как 10², а запись 10⁶ представляет число, начинающееся с единицы, за которой следуют шесть нулей, то есть один миллион. Оценивая величину таких чисел, достаточно помнить, что, скажем, число 10⁶ содержит в своей записи на один ноль больше, чем число 10⁵, и, следовательно, оно больше него в 10 раз. Для очень маленьких чисел, таких как размер атома, выраженный в сантиметрах — около 0,000000001 см, — учёные используют отрицательные показатели степени. Запись 10^—n означает единицу, делённую на 10ⁿ, то есть число типа 0,000… 0001, где единица стоит на n-й позиции после запятой. Таким образом, одна десятая будет записана как 10^-1, а одна миллиардная — как 10^-9.

Любое произвольное числовое значение может быть записано как число в диапазоне от 1 до 10, умноженное на десять в какой-то степени. Число 100 записывается как 10², в то время как число 135 можно представить в виде произведения 1,35∙100 и в экспоненциальной нотации записать как 1,35∙10². Второй сомножитель в этой записи называется порядком числа, он даёт нам представление о количестве цифр в обычной записи. Таким образом, числа 100 и 135 имеют один и тот же порядок. Первый сомножитель называется мантиссой — он говорит нам о том, где именно находится число в пределах указанного порядка, то есть является оно, например, числом 100 или числом 135.

Для физика порядок числа является наиболее важной характеристикой, поскольку он показывает масштаб явления, и экспоненциальная запись в этом отношении очень удобна, не говоря уже о том, что она просто короче. Гораздо легче воспринять число в форме 1,45962∙10¹³, чем 1 459 620 000 000 или «один триллион четыреста пятьдесят девять миллиардов шестьсот двадцать миллионов». Я рискну сделать ещё более сильное утверждение: числа, представляющие физический мир, имеют смысл только тогда, когда они записаны в экспоненциальной форме.

Есть и другие несомненные преимущества экспоненциальной записи. В частности, она сильно упрощает манипуляции с числами. Например, вы хотите перемножить два числа, скажем, 100 и 100. Традиционная запись выглядит так: 100×100 = 10 000. В экспоненциальной форме нахождение произведения 100×100 сведётся к следующей манипуляции: 10²х10² = 10⁽²⁺²⁾ = 10⁴ — фактически, мы заменяем умножение сложением. Аналогично и с операцией деления — вместо 1000:100 = 10 мы пишем: 10³:10² = 10^(3–2)= 10¹. Деление заменяется вычитанием. Эти простые правила оперирования со степенями десяти избавляют нас от необходимости постоянно считать количество знаков в перемножаемых числах, и единственное, для чего вам может понадобиться калькулятор, это для перемножения мантисс, то есть левых частей в экспоненциальной записи. Но поскольку мантиссы находятся в диапазоне от 1 до 10, то, помня таблицу умножения 10×10, вы всегда сможете сделать грубую прикидку результата в уме.

В мои задачи не входит научить вас искусству устного счёта, вместо этого я расскажу, как производить численные оценки. Если упрощение картины мира предполагает приближённое её описание, то экспоненциальная форма представления чисел лучше всего подходит для приблизительной оценки каких-то величин с точностью до порядка. Она позволяет быстро получить ответы на вопросы, которые при другом подходе были бы практически неразрешимыми. Грубые оценки помогают убедиться, что мы находимся на правильном пути. Они также позволяют сберечь время и силы, оберегая нас от выполнения ненужной работы. Одна известная байка рассказывает о некоем аспиранте, который потратил массу усилий, чтобы решить сложную систему уравнений, описывающую эволюцию Вселенной, чтобы получить в итоге один важный параметр. И на защите диссертации выяснилось, что этот же параметр получается за пару минут из общих соображений путём простой оценки.

Как сказал Энрико Ферми, «оценка по порядку величины позволяет вам ощутить почву под ногами». Ферми был последним из величайших физиков, который одинаково хорошо владел как теорией, так и техникой эксперимента. Он был одним из участников Манхэттенского проекта по созданию атомной бомбы и в числе прочего занимался проблемой получения управляемой цепной реакции деления атомных ядер. Он также был первым физиком, сумевшим построить теорию, описывающую цепную реакцию деления, за что удостоился Нобелевской премии. Его преждевременная смерть от рака, скорее всего, была вызвана воздействием радиации, изучением которой он занимался в те времена, когда её опасность для человеческого организма ещё не была установлена. Если когда-нибудь вы окажетесь в международном аэропорту имени Логана в Бостоне и по пути в город застрянете в пробке перед въездом в туннель, обратите внимание на мемориальную доску перед выездом на небольшой путепровод. Этот путепровод назван именем Энрико Ферми, и, на мой взгляд, очень показательно, что в то время как города называются именами президентов, а стадионы — именами спортсменов, именем Ферми названа дорога, поскольку в физике он был первопроходцем.

Я упомянул Ферми, потому что, будучи лидером группы физиков, работавших над Манхэттенским проектом в подвальной лаборатории, располагавшейся под футбольным полем Чикагского университета, он постоянно поднимал моральный дух руководимой им группы, разбавляя рутинную и тяжёлую работу интересными задачами, далеко не всегда имевшими отношение к физике. Энрико считал, что настоящий физик должен быть способен ответить на любой вопрос из любой области. Это не обязательно должен быть точный ответ — важно лишь разработать алгоритм, который позволил бы на основе имеющихся общих знаний оценить порядок величины. В качестве примера такой задачи можно привести вопрос, который часто задают на собеседовании в IT-компаниях: «Сколько настройщиков фортепиано проживают в настоящее время в Чикаго?»

Как бы подошёл к ответу на этот вопрос Энрико Ферми? Для начала он оценил бы численность населения Чикаго — допустим, пять миллионов человек. Из скольких человек состоит средняя чикагская семья? Предположим, что из четырёх. Тогда получается, что в Чикаго проживает (по порядку величины) около одного миллиона, или 10⁶ семей. У какой части семей дома есть фортепиано? Допустим, у каждой десятой. Значит, в Чикаго ориентировочно 100 000 фортепиано. Как часто необходимо их настраивать? Пускай раз в год. Сколько времени тратит настройщик на настройку одного инструмента? Явно не менее половины рабочего дня. Тогда, учитывая, что в выходные настройщик отдыхает, получится, что он способен настроить 500 фортепиано в год. Для того чтобы в течение года настроить 100 000 инструментов, понадобится:

100 000/500 = 1/5∙10⁵/10² = 1/5∙10³ = 0,2∙10³ = 2∙10² = 200 настройщиков.

Полученный результат не означает, что количество настройщиков в Чикаго в точности равно 200. Это оценка, полученная из общих соображений, но она даёт нам представление о порядке величины количества настройщиков. Если бы в реальности их оказалось менее 100 или более 1000, мы были бы сильно удивлены (на самом деле в Чикаго 600 настройщиков). Задумайтесь о том, что мы получили близкую к реальности оценку практически из ничего, из самых общих соображений, и снимите шляпу перед мощью этого метода.

Оценка по порядку величины может натолкнуть вас на новые идеи, которые в противном случае, возможно, никогда не пришли бы вам в голову. Чего больше: песчинок на пляже или звёзд на небе? Сколько людей на Земле чихают в течение одной секунды? За какое время вода и ветер смогут сточить до основания Эверест? Сколько человек в мире… (придумайте сами подходящий вопрос) за то время, пока вы читали эти строки?

Не менее важно и то, что оценка по порядку величины может принести вам озарение относительно тех вещей, суть которых вы пытаетесь понять. Человеческий мозг без специальной тренировки способен одновременно визуально зафиксировать в памяти не более двенадцати предметов, а чаще всего — не более шести. Когда вы видите шесть точек на грани игральной кости, вам нет необходимости их пересчитывать, вы и так понимаете, что их шесть. Но если бы у вас оказалась игральная кость с 20 гранями, то вы не сумели бы сразу определить, сколько точек находится на обращённой к вам грани: 17, 19 или 20, не пересчитывая их.

Даже если бы эти точки были нанесены в виде какого-нибудь регулярного узора, вы всё равно не смогли бы оценить их общее число, вместо этого вы оперировали бы, например, числом строк (4) и числом столбцов (5). Это происходит потому, что человек не способен легко и интуитивно представить себе число 20, несмотря на то что в повседневной жизни это число встречается достаточно часто: 20 пальцев на руках и ногах или 20 рабочих дней в месяце и т. д.

Оперируя очень большими или очень малыми числами, мы лишены способа наглядно представить, что они означают, не прибегая к оценке, которая позволила бы сопоставить исследуемое число с чем-то известным, что отличается от него не более чем в несколько раз, то есть с чем-то сравнимым по порядку величины. Один миллион может по порядку величины соответствовать числу людей, живущих в вашем городе, или количеству секунд, которые проходят за 10 дней. Миллиард по порядку величины соответствует населению Китая или количеству секунд, проходящих за 32 года. Сможете ли вы оценить, сколько раз вы слышите своё имя за время вашей жизни? Сколько килограммов пищи вы съедаете за десять лет? Удовольствие, получаемое от возможности шаг за шагом решать сложные, на первый взгляд, неразрешимые задачи, со временем вызывает сильное привыкание. Я думаю, что «кайф» подобного рода представляет собой большую часть удовольствия, которую получают физики от занятия физикой.

Экспоненциальная запись и оценка по порядку величины играют в физике неоценимую роль. Именно они в первую очередь и позволяют производить те самые упрощения, о которых я говорил в предыдущей главе. Если мы правильно представляем себе порядок величины, то мы уже понимаем большую часть из того, что нам необходимо понять. Я не хочу сказать, что вычисление всяких коэффициентов, входящих в уравнения типа 2π или 8/3, не важно, просто оценка порядка величины — это та самая лакмусовая бумажка, которая говорит, что мы на верном пути, а уже точно зная направление, можно начинать улучшать оценки, сравнивать предсказания с экспериментами и наблюдениями и совершенствовать теорию.

Теперь настало время пояснить, почему я сказал, что числа, отображающие реальные вещи в реальном мире, имеют смысл только будучи записанными в экспоненциальной форме. В первую очередь, потому что числа в физике, как правило, отражают то, что может быть измерено. Измеряя расстояние от Земли до Солнца, я могу выразить полученный результат двумя способами: 14 960 000 000 000 см или 1,4960∙10¹³ см. Для математика обе формы записи эквивалентны и представляют одно и то же число. Но для физика между числами 14 960 000 000 000 и 1,4960∙10¹³ существует принципиальная разница. Когда физик говорит, что расстояние от Земли до Солнца составляет 14 960 000 000 000 сантиметров, это означает, что оно в точности равно этому числу: не 14 959 790 562 739 и даже не 14 960 000 000 001 см, а ровно 14 960 000 000 000 см. Но это также означает, что мы знаем расстояние от Земли до Солнца с точностью до сантиметра!

Но это же абсурд, потому что расстояния от Аспена до Солнца (в полдень) и от Кливленда до Солнца (тоже в полдень) различаются на два с половиной километра — 250 000 сантиметров — из-за того, что Аспен и Кливленд располагаются на разной высоте над уровнем моря. Чтобы такое точное расстояние имело физический смысл, мы должны очень точно указать точку на поверхности Земли, в которой мы производим измерения. Даже если мы будем измерять расстояние между центром Земли и центром Солнца (самый разумный выбор), то это подразумевает, что мы предварительно измерили диаметры Земли и Солнца с точностью до сантиметра, не говоря уже о том, что произвести на практике измерения астрономических расстояний с такой точностью крайне проблематично, если вообще возможно.

Очевидно, что, написав число 14 960 000 000 000, мы на самом деле имели в виду приблизительное, а не точное значение. Но с какой точностью мы на самом деле знаем расстояние от Земли до Солнца? Подобного вопроса не возникает, когда мы записываем число в виде 1,4960∙10¹³ см. Принято считать, что в экспоненциальной записи в мантиссе сохраняются только достоверные цифры, и данная запись говорит о том, что реальное расстояние лежит в пределах между 1,49595∙10¹³ см и 1,49605∙10¹³ см. Если бы расстояние было известно нам с вдесятеро лучшей точностью, мы записали бы его в виде: 1,49600∙10¹³ см.

Таким образом, существует огромная разница между 1,4960∙10¹³ см и 14 960 000 000 000 см. Чтобы представить, насколько она огромна, подсчитаем абсолютную погрешность приведённого числа. Эта погрешность составляет 0,0001∙10¹³ см — один миллиард сантиметров, или десять тысяч километров, — почти диаметр Земли!

«И это физики называют точным результатом?» — спросите вы. Да. Несмотря на то что абсолютная величина погрешности — миллиард сантиметров — выглядит чудовищной, она составляет меньше одной десятитысячной расстояния от Земли до Солнца. Если бы вы с такой же точностью измерили свой рост, вы узнали бы его с точностью до двух десятых долей миллиметра.

Красота записи 1,4960∙10¹³ состоит ещё и в том, что множитель 10¹³ сразу же задаёт «масштаб» числа, а мантисса 1,4960 указывает на его точность. Чем больше десятичных разрядов содержит мантисса, тем точнее мы знаем физическую величину. Глядя на число, записанное в экспоненциальной форме, вы сразу же понимаете, чем можно пренебречь. Масштаб 10¹³ см говорит, что физические эффекты, проявляющиеся на масштабах в несколько сантиметров, метров, километров и даже тысяч километров, скорее всего, можно не учитывать. А как я говорил в предыдущей главе, самое главное в физике — это понимать, чем можно, а чем нельзя пренебречь.

До сих пор я игнорировал, возможно, наиболее важный факт, который придаёт числу 1,4960∙10¹³ см физический смысл. Это записанное после него сокращение «см». Без этих «см» мы бы не знали, к какой физической величине относится число, а сакраментальное «см» говорит о том, что это расстояние. Данная спецификация называется размерностью физической величины. Размерность связывает абстрактные математические числа с физическим миром реальных явлений. Сантиметры, дюймы, километры, световые года — это всё размерности длины, которые могут использоваться для измерения расстояний.

Вероятно, самым удивительным свойством окружающего мира, позволяющим упростить его картину, является то, что в природе существуют только три независимые размерные величины: длина, время и масса. Размерности всех остальных величин могут быть выражены через комбинацию трёх основных. Неважно, измеряете ли вы скорость в милях в час, метрах в секунду или стадиях в неделю, — всё это лишь различные способы выражения расстояния, делённого на время.

Это свойство имеет замечательные последствия. Из-за того что в природе существуют только три независимые размерные величины, количество комбинаций, которые можно из них сконструировать, ограничено. Это означает, что каждая физическая величина связана с любой другой физической величиной некоторым простым способом, и это существенно ограничивает количество различных математических соотношений, возможных в физике. Не побоюсь утверждать, что не существует более важного инструмента, используемого физиками, чем размерности физических величин. Размерности не только облегчают запоминание уравнений, но и существенно упрощают картину физического мира. Как я покажу позже, анализ размерностей даёт важный ориентир для разумной интерпретации той информации, которую мы получаем от наших органов чувств или измерительных приборов. Описывая физические величины, мы оперируем их размерностями.

Когда мы анализировали законы масштабирования сферического коня, мы работали с соотношениями размерностей длины и массы. Например, нам было важно установить, как соотносится изменение объёма коня с изменением его линейных размеров. Анализируя размерности, можно пойти дальше, чтобы понять, как оценить объём предмета произвольной формы. Как я уже говорил, неважно, какими единицами мы пользуемся для измерения объёма: кубическими дюймами, кубическими сантиметрами или кубическими футами, важно лишь, что все эти единицы кубические. Единицы, в которых измеряется объём, имеют размерность кубической длины, то есть [длина]×[длина]×[длина]. Таким образом, объём любого объекта может быть оценён путём выбора некоторой характеризующей этот объект длины d с последующим возведением её в куб: d³. Обычно этого достаточно, чтобы оценить порядок величины объёма. Например, объём сферы задаётся выражением V = π/6∙d³ ≈ ½∙d³, где d — её диаметр.

А вот пример простейшего анализа размерностей. Предположим, что вы забыли, что следует сделать, чтобы найти пройденное телом расстояние: умножить скорость на время или разделить. Посмотрев на размерности входящих в формулу величин, вы мгновенно получите правильный ответ. Размерность скорости — [метр]/[секунда], размерность длины — [метр]. Для того чтобы получить расстояние, то есть [метр], необходимо [метр]/[секунда] умножить на [секунда], а именно скорость умножить на время. Поколение за поколением студентов безуспешно зубрит сложные формулы, вместо того чтобы просто составить входящие в них физические величины так, чтобы размерность справа от знака равенства была такой же, как и размерность слева.

Следует обратить особое внимание на то, что анализ размерности никоим образом не гарантирует, что вы получите правильный ответ, но он гарантированно подскажет, когда вы ошибаетесь. Он как слега при переходе через болото: не факт, что, пользуясь ею, вы не заблудитесь, но зато наверняка не утонете.

Говорят, что фортуна благоволит подготовленному уму. Ничто не может быть более справедливым в отношении физики, и анализ размерности поможет подготовить ум к неожиданностям. Результат простого анализа размерностей часто оказывается настолько потрясающим, что может показаться магией. Для большей убедительности я приведу пример из современной физики, в котором известное и неизвестное оказались очень тесно переплетены. В этой истории анализ размерностей помог прийти к пониманию одной из четырёх фундаментальных сил природы — сильного взаимодействия, которое связывает кварки в протоны и нейтроны, являющиеся основными компонентами атомных ядер. При первом чтении апелляция к размерностям может показаться вам не очень понятной, но не беспокойтесь. Я привожу здесь эту историю, потому что она позволяет увидеть, насколько эффективно анализ размерностей способен подтолкнуть физическую интуицию. В моём рассказе красота вывода более важна, чем полученный результат.

Физики, изучающие элементарные частицы, пытающиеся найти основные кирпичи мироздания и объяснить фундаментальные взаимодействия, разработали систему единиц измерения, которая идеально приспособлена для анализа размерностей. В принципе три основные размерности — длина, время и масса — независимы, но на практике между ними есть фундаментальная связь, осуществляемая посредством так называемых фундаментальных физических констант. Например, если бы существовала некая универсальная константа, связывающая время и расстояние, я мог бы выразить расстояние через время путём простого умножения времени на эту константу. Впрочем, почему «если бы»? Такая константа действительно существует — это скорость света в вакууме. Один из постулатов созданной Эйнштейном теории относительности гласит, что скорость света в вакууме не зависит ни от скорости источника света, ни от скорости наблюдателя: как бы мы её ни измеряли, мы всегда будем получать одно и то же значение — в этом и состоит её универсальность. Эту константу принято обозначать латинской буквой c, и, как нетрудно догадаться, она имеет размерность длины, делённой на время. Если я умножу некий промежуток времени на c, я получу нечто, имеющее размерность длины, а именно — расстояние, которое свет проходит за это время. Таким способом мы можем любое расстояние выразить через время, которое требуется свету, чтобы пройти это расстояние. Например, расстояние от вашего плеча до локтя свет проходит за 10^-9 секунды, значит, вы можете считать, что расстояние от плеча до локтя составляет 10^-9 секунды. Любой наблюдатель, измеряющий расстояние в «световых секундах», получит то же самое значение.

Существование такой универсальной константы, как скорость света, позволяет установить взаимно однозначное соответствие между расстоянием и временем. Это позволяет исключить одну из этих размерностей из системы единиц. А именно: мы можем либо оставить только единицу длины, а время выражать через неё, либо наоборот. При этом очень удобно выбрать такие единицы измерения времени и расстояния, в которых скорость света оказывается равной единице. Например, мы можем выбрать в качестве единицы длины световую секунду, тогда скорость света будет равна одной световой секунде в секунду. В такой системе единиц расстояние и эквивалентное ему время будут выражаться одним и тем же числом!

Пойдём дальше. Если численное значение световой длины и соответствующего ей светового времени в построенной нами системе единиц одинаковы, то стоит ли рассматривать длину и время как величины разной размерности? Вместо этого можно присвоить расстоянию и времени одинаковые размерности, тогда скорость, которая суть расстояние, делённое на время, станет безразмерной величиной. Физически это эквивалентно тому, что мы бы измеряли скорость в (безразмерных) долях скорости света, то есть если я напишу, что скорость равна 1/2, это попросту будет означать, что она равна половине скорости света. Очевидно, что для корректного построения подобной системы нам понадобится универсальная эталонная скорость, относительно которой мы будем измерять все остальные скорости, — ну так скорость света и является таким универсальным эталоном.

Итак, после приравнивания скорости света к единице и объявления её безразмерной величиной у нас остаются только две независимых размерности: время и масса (или, если так будет удобнее, расстояние и масса). Одним из следствий такого необычного подхода является то, что он позволяет, помимо расстояния и времени, приравнять размерности и других величин. Например, знаменитая формула Эйнштейна E = mc² устанавливает эквивалентность массы и энергии. В нашей системе единиц, где скорость света c равна безразмерной единице, размерность массы оказывается такой же, как и размерность энергии. Давайте подумаем, что формально делает формула Эйнштейна. Она устанавливает взаимно однозначное соответствие между массой и энергией, то есть если у нас что-то обладает некоей энергией, то это что-то обладает эквивалентной этой энергии массой, и наоборот. Если переводной коэффициент между массой и энергией становится безразмерной единицей, то величина массы становится тождественно равной величине энергии. Это освобождает нас от необходимости использовать для измерения массы величин типа килограмма или фунта, мы можем измерять её в тех же единицах, в которых измеряем энергию: в джоулях или калориях. Именно так и поступают физики, изучающие элементарные частицы: они измеряют массы частиц в электрон-вольтах. Электронвольт — это энергия, которую приобретает электрон, если его разогнать разностью потенциалов в один вольт. Вместо того чтобы записывать массу электрона как 10^-31 г, физики записывают её как 0,511 МэВ (мегаэлектронвольт). Поскольку в физике элементарных частиц учёные постоянно имеют дело с процессами, в которых масса частиц преобразуется в энергию и обратно, то совершенно разумно и логично использовать для измерения массы те же единицы, что и для измерения энергии, и не брать в голову никакие переводные коэффициенты из джоулей в килограммы. Существует важное правило: всегда следует использовать такие единицы измерения, которые дают наилучшее представление о масштабе явления. В ускорителях частицы разгоняются до скоростей, близких к скорости света, поэтому использование системы единиц, в которой скорость света равна единице, для таких задач очень удобно и практично. Для описания же явлений повседневной жизни такая система, наоборот, оказывается непрактичной и неудобной, поскольку приводит к необходимости оперировать очень маленькими числами. Например, скорость реактивного самолёта в единицах скорости света составляет порядка 0,000001 = 10^-6.

Но это ещё не всё. Существует ещё одна фундаментальная физическая постоянная, её принято обозначать буквой h и называть постоянной Планка. Немецкий физик Макс Планк был одним из отцов-основателей квантовой механики. Он ввёл эту константу, чтобы связать энергию кванта с его частотой, а значит, постоянная Планка устанавливает связь между энергией и временем или, если вам хочется, между массой и расстоянием. Действуя так же, как мы поступили со скоростью света, примем численное значение постоянной Планка равным безразмерной единице. Что получится? Из всех размерностей у нас останется только размерность энергии, поскольку теперь мы можем выразить через энергетические единицы, например через электрон-вольты, не только энергию, но и массу, и время, и расстояние — и все остальные физические единицы измерения. Постоянная Планка связывает энергию и частоту: Е = hν, частота имеет размерность [1/секунда], тогда время в энергетических единицах будет иметь размерность [1/электронвольт]. В физике часто вместо постоянной h используется постоянная ħ, которая равна h/(2π), просто потому что так удобнее. В системе единиц, в которой с = ħ = 1, одна секунда будет равна 1,5∙10¹⁵/эВ — обратите внимание, что электрон-вольты стоят в знаменателе, обычно в таких случаях используют отрицательные показатели степени и пишут: 1,5∙10¹⁵ эВ^-1.

В итоге мы создали систему, в которой три основные размерности свели к одной. Теперь мы можем описать весь физический мир, используя только размерность массы, или только размерность длины, или только размерность времени — не принципиально, какую размерность мы выберем, это уже будет результат произвольного соглашения. В физике высоких энергий удобно использовать в качестве базовой размерность энергии. Например, объём, имеющий в привычной системе единиц размерность [длина³], в новой системе, в которой с = ħ = 1, будет иметь размерность [1/энергия³], потому что длина в этой системе имеет ту же размерность, что и время, а время имеет размерность, обратную размерности энергии. Численно 1 м³ будет равен 1,3∙10²⁰ эВ^-3.

На первый взгляд описанный подход выглядит непривычно, но вся его прелесть состоит в том, что, оставляя только один независимый размерный параметр, мы можем существенно упростить анализ и свести очень сложные явления к одной физической величине. Порой это выглядит как настоящая магия. Например, предположим, что мы обнаружили новую элементарную частицу, масса которой в три раза превышает массу протона, или в энергетических единицах составляет около 3 миллиардов электрон-вольт — 3 ГэВ (гигаэлектрон-вольта). Если эта частица нестабильна, то каково ожидаемое время её жизни? Может показаться, что, не зная никаких подробностей о структуре частицы, сделать подобную оценку невозможно. Однако, используя анализ размерностей, можно выдвинуть кое-какие предположения.

Единственная размерная характеристика, присутствующая в этой задаче, — масса, или, что эквивалентно, энергия покоя частицы. Поскольку размерность времени в нашей новой системе единиц эквивалентна обратной размерности массы, разумная оценка времени жизни частицы будет составлять k/(3 ГэВ), где k — некий безразмерный параметр.

В отсутствие какой бы то ни было дополнительной информации нам не остаётся ничего лучшего, как надеяться, что этот параметр не очень сильно отличается от единицы. Мы можем перевести электрон-вольты в привычные секунды, используя соотношение: 1/1 эВ = 6,5∙10^-16 с. Таким образом, время жизни нашей новой частицы должно быть порядка k∙10^-25 секунды.

Разумеется, в действительности никакой магии тут нет. Мы не получили что-то из ничего, просто анализ размерностей дал характерный масштаб нашей задачи. Этот анализ говорит, что «естественное время жизни» нестабильной частицы такой массы составляет порядка k∙10^-25 секунды, подобно тому как «естественное время жизни» человека составляет порядка k∙75 лет. Все реальные физические (или в последнем случае биологические) оценки содержат неизвестный параметр k. Если вдруг этот параметр оказывается очень малым или очень большим, то перед нами встаёт новая интересная задача: понять, почему в каком-то конкретном случае параметр существенно отличается от единицы.

Анализ размерностей даёт нам очень важную информацию для размышлений. Если параметр k сильно отличается от единицы, это говорит о том, что за кулисами действует какая-то дополнительная сила — очень слабая или, наоборот, очень сильная, приводящая к тому, что реальное время жизни начинает отличаться от естественного, получаемого путём анализа размерностей. Допустим, мы обнаружили суперконя, размеры которого в 10 раз превышают размеры обычного коня, а вес составляет всего полкилограмма. Из приведённых ранее масштабных соображений суперконь должен весить в 1000 раз больше обычного коня, значит, — заключаем мы, — наблюдаемый сверхлёгкий суперконь состоит из очень экзотического вещества. И правда — многие из наиболее интересных физических открытий были сделаны в результате обнаружения несоответствия между наблюдаемыми фактами и результатами простой экстраполяции явлений на другие масштабы. Важно понимать, что, не обнаружь мы этого несоответствия, мы бы, возможно, не имели ни малейшего понятия о том, что тут можно найти что-то новое и интересное!

В 1974 году произошло одно знаменательное и драматическое событие. В течение 1950-х и 1960-х годов энергии, до которых разгонялись частицы в ускорителях, неуклонно росли. Помимо энергий росло и количество одновременно ускоряемых частиц, что позволило перейти от столкновений частиц с неподвижной мишенью к столкновениям встречных пучков, а это, в свою очередь, дополнительно увеличило энергии сталкивающихся частиц.

В ходе этих экспериментов было обнаружено множество неизвестных ранее типов частиц. Когда количество новых частиц перевалило за сотню, теоретики схватились за голову, но в начале 1960-х годов Мюррей Гелл-Ман в Калтехе разработал кварковую модель, позволившую навести некоторый порядок в открытом экспериментаторами хаосе. Согласно его предположению, все вновь открытые частицы можно составить из простых комбинаций фундаментальных объектов, которые Гелл-Ман назвал кварками. Частицы, получаемые в ускорителях, можно было разделить на состоящие из трёх кварков и на состоящие из кварка и антикварка. Новые комбинации, составленные из того же набора кварков, из которых состоят протон и нейтрон, согласно предсказаниям должны были образовывать нестабильные частицы с массами порядка массы протона. Таки частицы были действительно обнаружены, и их время жизни оказалось довольно близким к нашей оценке — 10^-24 секунды.

Наша оценка была 10^-25 секунды, значит, константа k составляет около 10 — не слишком далеко от единицы. Всё, казалось бы, хорошо, но оставались две неприятности. Во-первых, при распаде частиц всегда образовывались другие частицы, состоящие из кварков, но ни разу ни в одном процессе никому не удалось получить один свободный кварк, а во-вторых, из-за того, что силы взаимодействия между кварками были велики, никому не удавалось точно рассчитать, как они должны себя вести.

В 1973 году было сделано важное теоретическое открытие. Работая над теорией, которая позволила бы объединить электромагнитное и слабое взаимодействие, Дэвид Гросс и Фрэнк Вильчек из Принстона и независимо от них Дэвид Политцер из Гарварда разработали очень привлекательную теорию, которая претендовала на роль теории сильного взаимодействия. В этой теории каждый кварк мог иметь одно из трёх различных свойств, которые были в рабочем порядке условно названы «цветами», а сама теория получила название квантовой хромодинамики, или сокращённо КХД. Самым удивительным свойством взаимодействия между кварками оказалось то, что, когда они приближались друг к другу, сила притяжения между ними уменьшалась, а когда удалялись — увеличивалась. До сих пор ни в одной теории сила взаимодействия не вела себя таким странным образом.

Наконец появилась надежда, что кто-нибудь сумеет выполнить расчёты, на основании которых можно будет сравнить предсказания теории с экспериментом. Поскольку на близких расстояниях силы взаимодействия между кварками малы, то можно начать расчёт с невзаимодействующих кварков, а потом добавлять методом последовательных приближений всё более и более сильные взаимодействия и в конце получить относительно точное описание их взаимодействия.

В то время как теоретики начали исследовать особенность поведения кварков, получившую название асимптотической свободы, экспериментаторы из Нью-Йорка и Калифорнии разгоняли частицы в ускорителях до всё более и более высоких энергий.

И вот в ноябре 1974 года, с разницей в несколько недель, две разные группы экспериментаторов обнаружили новую частицу с массой примерно в три раза больше массы протона. Но привлекла к себе внимание частица не своей массой, а необычно большим временем жизни, которое в 100 раз превышало время жизни других частиц с похожими массами. Один из физиков сравнил этот факт с обнаружением затерянного в джунглях племени людей, продолжительность жизни в котором составляет 10 000 лет.

Пытаясь объяснить этот феномен, Политцер и его коллега Том Эпплкуист пришли к выводу, что обнаруженная тяжёлая частица состоит из нового типа кварков, предсказанных теоретически несколькими годами ранее и названных очарованными кварками. Большое время жизни связанного состояния этих кварков напрямую следовало из асимптотической свободы кварков в КХД. Если очарованный кварк и очарованный антикварк тяжелее кварков, из которых состоят протоны и нейтроны, то в связанном состоянии они находятся гораздо ближе друг к другу, а значит, силы взаимодействия между ними гораздо слабее.

Это приводит к тому, что им требуется большее время, чтобы «найти» друг друга и проаннигилировать. Грубая оценка времени жизни такого связанного состояния была получена путём масштабирования силы взаимодействия кварков от размера протона до предполагаемого размера новой частицы. Оценка по порядку величины совпала с экспериментальными данными. Так КХД получила своё первое экспериментальное подтверждение.

В последующие годы эксперименты, проведённые при ещё более высоких энергиях сталкивающихся частиц, показали, что используемое в расчётах приближение является достаточно надёжным, и многократно подтвердили существование предсказанной квантовой хромодинамикой асимптотической свободы. Несмотря на то что до сих пор никому так и не удалось выполнить полный и точный расчёт поведения кварков на таких расстояниях, когда их взаимодействие становится очень сильным, количество полученных экспериментальных доказательств уже настолько велико, что сегодня никто не сомневается в справедливости КХД. В 2004 году Гросс, Вильчек и Политцер были удостоены Нобелевской премии за предсказание асимптотической свободы, открывшей дорогу к экспериментальной проверке квантовой хромодинамики. Без ключевых соображений, основанных на анализе размерностей физических величин, это открытие, вполне возможно, могло и не состояться или, по крайней мере, задержаться на долгие годы. Анализ размерностей применим не только в физике элементарных частиц, он является универсальным методом, который даёт нам точку опоры, позволяющую протестировать наше представление о реальности.

Хотя физическое мировоззрение и начинается с чисел, используемых для описания природы, оно не останавливается на них. Помимо чисел физикам нужен язык, при помощи которого они могли бы оперировать числами, как словами, и этим языком является математика. Сразу предвижу чисто практический вопрос: почему бы не пользоваться более естественным языком? Но у нас нет выбора. Ещё Галилей 400 лет назад писал: «Философия написана в величественной книге (я имею в виду Вселенную), которая постоянно открыта нашему взору, но понять её может лишь тот, кто сначала научится постигать её язык и толковать знаки, которыми она написана. Написана же она на языке математики, и знаки её — треугольники, круги и другие геометрические фигуры, без которых человек не смог бы понять в ней ни единого слова; без них он был бы обречён блуждать в потёмках по лабиринту».

Сегодня утверждение, что математика является языком физики, воспринимается как банальность, наподобие той, что французский язык является языком любви. Но это утверждение никак не объясняет, почему мы не можем перевести на другой язык математические выражения так же легко, как стихи Бодлера. В вопросах любви даже те из нас, чей родной язык не является французским, разбираются достаточно хорошо и без перевода, чего нельзя сказать о математических вычислениях.

Дело в том, что математика — это больше, чем просто язык. Чтобы показать, насколько больше, я одолжу один аргумент у Ричарда Фейнмана. Помимо того, что Фейнман был харизматиком, он являлся ещё и одним из величайших умов среди физиков-теоретиков двадцатого столетия. Фейнман обладал редким даром просто и понятно объяснять сложные вещи, чем, мне кажется, отчасти объясняется тот факт, что у него всегда был собственный способ понимания и собственный способ вывода почти всех результатов классической физики.

Объясняя роль математики в физике, он, в свою очередь, приводил в пример Исаака Ньютона. Величайшим открытием Ньютона был, безусловно, закон всемирного тяготения. Показав, что та же сила, которая удерживает нас на поверхности Земли, отвечает за движения всех небесных объектов, Ньютон сделал физику универсальной наукой. Он показал, что у нас есть возможность описать не только управляющие нами законы и наше место во Вселенной, но и саму Вселенную. Мы сегодня склонны принимать это как должное, но один из самых замечательных законов во Вселенной говорит нам, что та же самая сила, которая управляет полётом бейсбольного мяча, управляет движением Земли вокруг Солнца, движением Солнца вокруг центра Галактики, движением Галактики относительно других галактик и эволюцией самой Вселенной, хотя относительно справедливости последнего утверждения — насчёт Вселенной — вопрос пока остаётся открытым.

Ньютоновский закон всемирного тяготения может быть сформулирован в словесной форме: сила гравитационного притяжения между двумя объектами направлена вдоль линии, соединяющей эти объекты, пропорциональна произведению масс объектов и обратно пропорциональна квадрату расстояния между ними. Словесное определение выглядит громоздким, но это не важно. В сочетании со вторым законом Ньютона, утверждающим, что тело реагирует на действующую на него силу путём изменения скорости в направлении действия силы, и это изменение пропорционально величине силы и обратно пропорционально массе тела, закон всемирного тяготения позволяет описать всё. Любое движение любого количества тяготеющих тел может быть выведено из этих двух законов. Но как? Я мог бы дать эту формулировку лучшему в мире лингвисту и попросить его вывести из неё возраст Вселенной, используя семантические правила, но подозреваю, Вселенная прекратит своё существование раньше, чем ему удастся получить ответ.

Суть в том, что математика представляет собой набор утверждений и выводов, подчинённых правилам логики. Например, Иоганн Кеплер в начале XVII века, проанализировав множество наблюдательных данных, пришёл к выводу, что планеты движутся вокруг Солнца особым образом. Если соединить планету с Солнцем отрезком прямой, то этот отрезок будет за одинаковые промежутки времени «заметать» одинаковые площади. Математически можно показать, что из этого утверждения следует, что, когда планета находится ближе к Солнцу, она движется по своей орбите быстрее, чем когда она находится дальше. Ньютон, в свою очередь, показал, что открытый Кеплером закон может быть строго математически получен из приведённых выше формулировок закона всемирного тяготения и второго закона Ньютона.

Попробуйте, если сумеете, вывести второй закон Кеплера из законов Ньютона, используя только правила английского (или русского) языка… Но при помощи математики, в данном случае на основе простых геометрических соображений, вы сделаете это за несколько минут. За подробностями обратитесь к «Математическим началам натуральной философии» Ньютона, а ещё лучше — прочитайте замечательную книгу Фейнмана «Характер физических законов».

Ключевой момент этой истории состоит в том, что Ньютон, возможно, никогда не сумел бы вывести закон всемирного тяготения, если бы не соединил при помощи математики открытый Кеплером закон движения планет с предположением, что между планетами и Солнцем действует сила притяжения. Этот момент является решающим для развития науки. Не имея математической основы под натуральной философией, к которой во времена Ньютона относили физику, невозможно построить логичную и согласованную теорию. Синтез математических выводов с наблюдаемой физической реальностью имеет основополагающее значение для построения научной картины реальности.

Я думаю, что вполне уместной будет литературная аналогия. Работая над этой главой, я читал роман канадского писателя Робертсона Дэвиса «Пятый персонаж». В нескольких предложениях он кратко суммирует то, что произошло с его персонажем: «Солдаты пришли в крайнее изумление, что я способен на такие вещи, чем привели в крайнее изумление меня самого… В их головах просто не укладывалось, что человек может иметь и другую, вроде бы совсем противоположную грань. Мне кажется, что я всегда считал самоочевидным, что каждый человек имеет по крайней мере две — если не двадцать две — грани…»

Позвольте теперь пояснить, к чему я привёл эту цитату, на личном примере. Одной из многих вещей, которые я приобрёл благодаря своей жене, было открытие новых способов видения мира. Мы вышли из совершенно разных слоёв общества. Она родилась в маленьком городке, а я — в мегаполисе. Те, кто, подобно мне, вырос в мегаполисе, склонны воспринимать окружающих не так, как те, кто вырос в небольшом городке. Подавляющее большинство людей, которых вы встречаете ежедневно в большом городе, фигурально выражаясь, «одномерны». Вы воспринимаете мясника как мясника, почтальона как почтальона, врача как врача и так далее. Но в маленьком городке вам не удастся встретить просто мясника или просто почтальона, потому что все они, помимо всего прочего, ещё и ваши соседи. Врач может по совместительству оказаться горьким пьяницей, а живущий напротив бабник — прекрасным учителем английского языка в местной школе. Подобно главному герою романа Дэвиса, я открыл для себя, что люди не могут быть легко классифицированы на основании какой-нибудь одной черты характера или рода занятий. Только когда осознаёшь всю многогранность человека, получаешь возможность понять его.

Аналогично, каждый физический процесс во Вселенной — «многомерен». Только охватив взглядом множество, на первый взгляд, различных, а на самом деле эквивалентных описаний какого-нибудь явления, можно понять, «как это работает». Мы не способны понять природу, наблюдая только одну её сторону. Хорошо это или плохо, но только математические соотношения позволяют нам увидеть целое на фоне частей, увидеть лес за деревьями. Математика позволяет представить сложный мир в виде простого сферического коня.

В каком-то смысле математика усложняет мир, открывая нам разные грани реальности. Но, поступая таким образом, она в действительности упрощает его для нашего понимания. Нет необходимости держать в голове одновременно все грани реальности, математика позволяет легко переходить от одной грани к другой. Если роль физики состоит в том, чтобы сделать для нас более понятной природу, то роль математики в том, чтобы сделать для нас более понятной физику.

Позволяя описать одно и то же явление разными способами, математика открывает для нас новые пути исследования природы, позволяя взглянуть на что-то давно известное с новой стороны. Кроме того, каждая новая грань реальности открывает возможность расширения наших представлений за пределы известного явления, приводя к новым открытиям. Было бы упущением с моей стороны не привести один известный пример, который не перестаёт восхищать меня вот уже двадцать пять лет, с тех пор, как я впервые узнал его от Фейнмана.

Речь пойдёт о таком всем знакомом, но вместе с тем загадочном явлении, как мираж. Любой, кто когда-либо ехал на автомобиле в жаркий день по длинному прямому участку шоссе, наблюдал, как впереди то и дело возникают, а при приближении пропадают лужи, в которых отражается небо и окружающий пейзаж. Это менее экзотический вариант того, что видят бредущие через пустыню путники, бросающиеся к иллюзорному озеру, которое исчезает при их приближении.

Существует стандартное объяснение возникновения миража, заключающееся в том, что световые лучи преломляются, проходя границу двух сред. Это, в частности, объясняет, почему, стоя в воде, вы выглядите меньше ростом. Лучи света преломляются, пересекая поверхность воды, и вы видите собственные ступни выше, чем они расположены на самом деле:

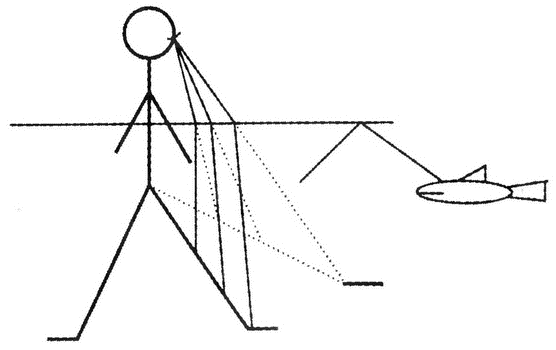
Когда свет выходит из более плотной среды в менее плотную, как показано на рисунке (проходит путь от ваших ног в воде до ваших глаз в воздухе), он всегда преломляется в сторону более плотной среды. Если угол, под которым свет падает на границу сред, слишком большой, то свет вообще не выходит из более плотной среды, а испытывает полное внутреннее отражение. В результате акула, собирающаяся перекусить вами, оказывается скрытой от вашего взора.

В знойный день воздух над поверхностью дороги сильно нагревается и становится гораздо менее плотным. По мере удаления от разогретого асфальта воздух становится холоднее, и его плотность увеличивается. Когда луч света, приходящего от неба, приближается к поверхности дороги, он попадает во всё более и более разрежённые слои воздуха и испытывает преломление, отклоняясь в сторону более плотного, то есть холодного воздуха, пока не отразится обратно вверх.

Таким образом, разогретая дорога представляется вам как бы зеркалом, отражающим голубое небо. Если вы внимательно присмотритесь к миражу, то увидите, что это «зеркало» на самом деле расположено не на самой поверхности дороги, а чуть выше неё.

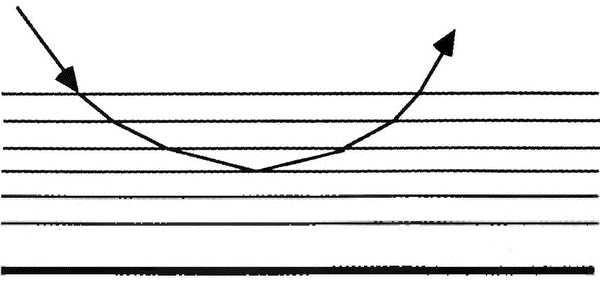
Это стандартное объяснение миража, и оно является вполне удовлетворительным, хотя и не особо вдохновляющим. Но существует другое объяснение того же явления, которое математически эквивалентно первому, но рисует всю картину существенно иначе. Это объяснение основано на принципе наименьшего времени, предложенном французским математиком Пьером Ферма в 1650 году, который гласит, что свет всегда распространяется по пути, для прохождения по которому ему требуется минимальное время.

Этот принцип прекрасно объясняет, почему свет в однородной среде распространяется по прямой линии, но как с его помощью объяснить мираж? Допустим, нам известно, что скорость света в менее плотном воздухе больше, чем в более плотном. Поскольку воздух вблизи дороги более горячий и менее плотный, то и свет вблизи дороги движется быстрее, чем вдали от неё. Теперь представьте себе луч света, который собирается попасть из точки A в точку В. Какой путь он выберет, руководствуясь принципом Ферма?

Один из возможных путей — это отрезок прямой линии, соединяющий точки A и B. Однако в этом случае свету придётся проделать весь путь в холодном и плотном воздухе. Другой возможный путь показан на рисунке. В этом случае свет проходит большее расстояние, но он проводит большее время в менее плотном воздухе вблизи поверхности дороги, где он движется быстрее. Вычислив общее время, затраченное светом в каждом из двух вариантов, вы обнаружите, что кривой путь оказывается более быстрым, чем прямой.

Если задуматься, то всё это очень странно. Откуда свет заранее может знать, какой путь является самым быстрым? Не может же он «обнюхать» все возможные пути, прежде чем окончательно выбрать правильный? Разумеется, нет. Он просто повинуется локальным физическим законам, которые говорят ему, что следует делать в каждый конкретный момент, а математически (после интегрирования) это всегда оказывается путь, требующий минимального времени. В этом выводе есть что-то, вызывающее чувство глубокого удовлетворения. Он кажется более фундаментальным, чем альтернативное описание с позиции преломления света в различных слоях воздуха. Так оно и есть. Теперь мы понимаем, что законы движения любых объектов могут быть выражены в форме, похожей на принцип Ферма. Кроме того, эта новая форма выражения классических ньютоновских законов движения привела Фейнмана к разработке новых методов описания квантово-механического поведения частиц.

Путём предоставления различных, но эквивалентных способов описания мира математика открывает перед нами новые пути понимания природы. Новый способ описания — это больше, чем пересказ другими словами. Новая картина может помочь нам обойти препятствия, которые представлялись непреодолимыми с прежних позиций. Например, методы, основанные на принципе, аналогичном принципу Ферма, позволили применить квантовую механику в таких областях, в которых она до сих пор считалась неприменимой. В частности, стоит упомянуть недавние попытки Стивена Хокинга понять, может ли квантовая механика привести к переосмыслению общей теории относительности.

Поскольку математические соотношения играют ключевую роль в нашем понимании природы, открывая новые способы описания мира, то неизбежно возникает следующий вопрос, наедине с которым я хочу оставить вас в конце этой главы. Если описание природы является математической абстракцией, то какой смысл имеет утверждение, что мы понимаем Вселенную? Например, в каком смысле законы Ньютона объясняют, почему физические тела движутся? Обратимся снова к Ричарду Фейнману:

В конце концов, мы никогда не сможем пройти дальше установления каких-то законов и никогда не сможем узнать, почему они именно такие. Но мы успешно открываем эти законы путём вычленения простого из сложного и отбрасывания несущественного, руководствуясь теми правилами, о которых я рассказывал в этой и предыдущей главах. И когда мы пытаемся понять мир тем способом, которым это делают физики, это всё, что мы можем надеяться сделать. Тем не менее, если мы очень постараемся и удача окажется на нашей стороне, мы сможем, по крайней мере, получить удовольствие от прогнозирования того, что произойдёт в ситуации, которую никто никогда раньше не наблюдал. Поступая таким образом, мы можем надеяться обнаружить новые скрытые физические закономерности, предсказав их при помощи математики, и надо признать, что это делает процесс познания мира чрезвычайно увлекательным занятием.