Книга: Жизнь 3.0. Быть человеком в эпоху искусственного интеллекта
Назад: Что такое память?
Дальше: Что такое обучение?
Что такое вычисление?
Итак, мы видели, как физический объект может хранить информацию. Но как он может вычислять?
Вычисление – это переход памяти из одного состояния в другое. Иными словами, вычисление использует информацию, чтобы преобразовывать ее, применяя к ней то, что математики называют функцией. Я представляю себе функцию этакой мясорубкой для информации, как показано на рис. 2.5: вы закладываете в нее сверху исходную информацию, поворачиваете ручку, и оттуда вылезает переработанная информация. Вы можете повторять раз за разом одно и то же действие, получая при этом все время что-то разное. Но сама по себе обработка информации полностью детерминирована в том смысле, что если у вас на входе все время одно и то же, то и на выходе вы будете получать все время один и тот же результат.
В этом и заключается идея функции, и хотя такое определение кажется слишком простым, оно до невероятия хорошо работает. Некоторые функции совсем тривиальные, вроде той, что зовется NOT: у нее на входе один бит, и она заменяет его другим, превращая ноль в единицу, а единицу в ноль. Функции, которые мы изучаем в школе, обычно соответствуют кнопочкам на карманном калькуляторе, на входе при этом может быть одно число или несколько, но на выходе всегда одно: например, это может быть x2, то есть при вводе числа выводится результат его умножения на себя. Но есть и исключительно сложные функции. Например, если вы располагаете функцией, у которой на входе произвольное положение фигур на шахматной доске, а на выходе – наилучший следующий ход, то у вас есть шанс на победу в компьютерном чемпионате мира по шахматам. Если вы располагаете функцией, у которой на входе состояние всех финансовых рынков мира, а на выходе – список акций, которые следует покупать, то вы скоро сильно разбогатеете. Многие специалисты по искусственному интеллекту видят свою задачу исключительно в том, чтобы придумать, как вычислять некоторые функции для любых начальных условий. Например, цель машинного перевода заключается в том, чтобы, взяв последовательность бит, представляющую исходный текст на одном языке, преобразовать ее в другую последовательность бит, представляющую тот же текст, но на другом языке, а цель создания систем автоматизированного распознавания изображений заключается в том, чтобы преобразовывать последовательность бит, представляющую какую-то картинку на входе, в последовательность бит, представляющую собой текст, который эту картинку описывает (рис. 2.5).
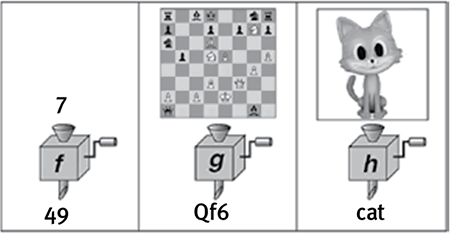
Рис. 2.5
Каждое вычисление использует информацию на входе, чтобы преобразовывать ее, выполняя над ней то, что математики называют функцией. У функции f (слева) на входе последовательность бит, представляющих число; в результате вычислений она дает на выходе его квадрат. У функции g (в центре) на входе последовательность бит, представляющих позицию на шахматной доске; в результате вычислений она дает на выходе лучший ход для белых. У функции h (справа) на входе последовательность бит, представляющих изображение, в результате вычислений она дает на выходе соответствующую текстовую подпись.
Другими словами, если вы можете вычислять достаточно сложные функции, то вы сумеете построить машину, которая будет весьма “умной” и сможет достигать сложных целей. Таким образом, нам удается внести несколько большую ясность в вопрос о том, как может материя быть разумной, а именно: как могут фрагменты бездумной материи вычислять сложные функции.
Речь теперь идет не о неизменности надписи на поверхности золотого кольца и не о других статических запоминающих устройствах – интересующее нас состояние должно быть динамическим, оно должно меняться весьма сложным (и, хорошо бы, управляемым/программируемым) образом, переходя от настоящего к будущему. Расположение атомов должно быть менее упорядоченным, чем в твердом и жестком теле, где ничего интересного не происходит, но и не таким хаотичным, как в жидкости или в газе. Говоря точнее, мы бы хотели, чтобы наша система восприняла начальные условия задачи как свое исходное состояние, а потом, предоставленная самой себе, как-то эволюционировала, и ее конечное состояние мы бы могли рассматривать как решение данной ей задачи. В таком случае мы можем сказать, что система вычисляет нашу функцию.
В качестве первого примера этой идеи давайте построим из нашей неразумной материи очень простую (но от этого не менее важную) систему, вычисляющую функцию NAND и потому получившую название гейт NAND. У нее на входе два бита, а на выходе один: это 0, если оба бита на входе 1, во всех остальных случая – это 1. Если в одну сеть с батареей и электромагнитом мы вставим два замыкающих сеть ключа, то электромагнит сработает тогда, и только тогда, когда оба ключа замкнуты (находятся в состоянии “on”). Давайте поместим под ним еще один ключ, как показано на рис. 2.6, так что магнит, срабатывая, всякий раз будет размыкать его. Если мы интерпретируем первые два ключа как два бита на входе, а третий – как бит на выходе, то мы и получим то, что назвали гейтом NAND: третий ключ будет разомкнут только тогда, когда первые два замкнуты. Есть очень много более практичных способов сделать гейт NAND – например, с помощью транзисторов, как показано на рис. 2.6. В нынешних компьютерах гейты NAND чаще всего встроены в микросхемы или иные компоненты, выращенные из кристаллов кремния.
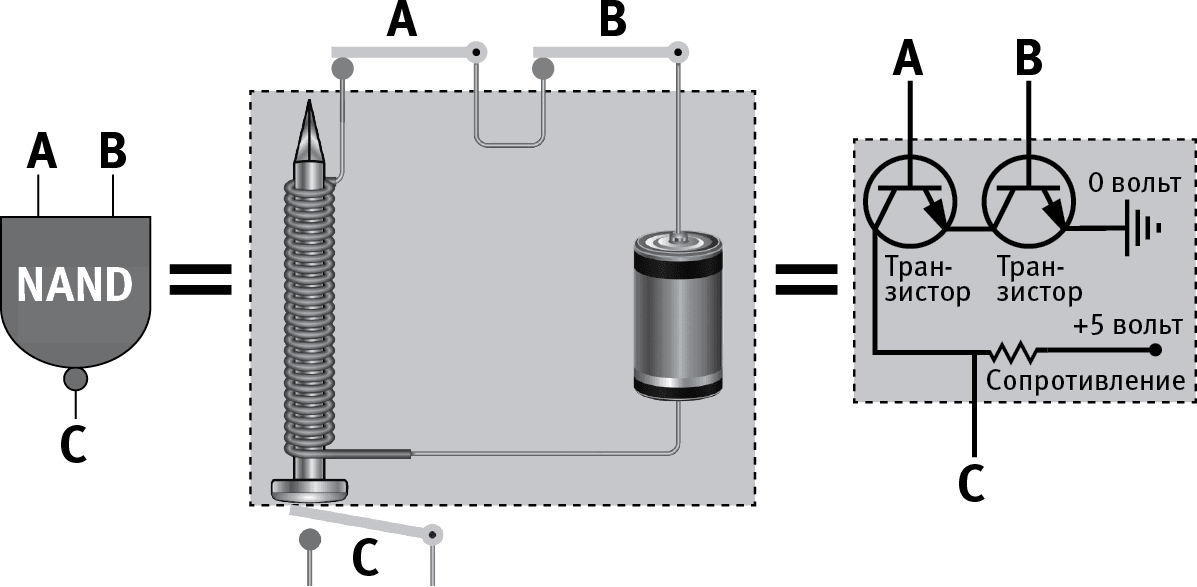
Рис. 2.6
Логический вентиль (гейт) NAND по заданным на входе двум битам А и В вычисляет третий бит С в соответствии с правилом: C = 0, если A = B = 1, и C = 0 в любом другом случае, – и посылает его на выход. В качестве гейта NAND можно использовать много различных физических устройств. В электрической цепи на средней части рисунка ключи А и В соответствуют битам на входе со значениями 0 при размыкании и 1 при замыкании. Когда они оба замкнуты, идущий через электромагнит ток размыкает ключ С. На схеме в правой части рисунка битам соответствуют значения потенциалов – 0, когда потенциал равен нулю, и 1, когда потенциал равен 5 вольтам. При подаче напряжения на базы обоих транзисторов (А и В) потенциал в точке С падает практически до нуля.
В информатике есть замечательная теорема, которая утверждает, что гейт NAND универсален: то есть вычисление любой вполне определенной функции может быть осуществлено гейтами NAND, соединенными друг с другом. Так что если у вас есть достаточное количество гейтов NAND, вы можете собрать из них устройство, вычисляющее все что угодно! На случай, если у вас возникло желание посмотреть, как это работает, у меня есть схема (рис. 2.7), на которой вы увидите, как умножаются числа при помощи одних только гейтов NAND.
Исследователи из MIT Норман Марголус и Томмазо Тоффоли придумали слово “computronium” (компьютрониум), обозначающее любую субстанцию, которая может выполнять любые вычисления. Мы только что убедились, что создать компьютрониум не так уж и сложно: эта субстанция всего лишь должна быть способна соединять гейты NAND друг с другом любым желаемым способом. Разумеется, существуют и мириады других компьютрониумов. Например, еще один легко создать из предыдущего, заменив все гейты NAND на NOR: у него на выходе будет 1 только тогда, когда на оба входа подается 0. В следующем разделе мы обсудим нейронные сети, которые также способны выполнять произвольные вычисления, то есть и они ведут себя как компьютрониум. Ученый и предприниматель Стивен Вольфрам показал, что то же может быть сказано о простых устройствах, получивших название клеточных автоматов, которые периодически подправляют каждый бит в зависимости от того, в каком состоянии находятся биты по соседству. А еще в 1936 году Алан Тьюринг доказал в своей ставшей ключевой статье, что простая вычислительная машина (известная сейчас как “универсальный компьютер Тьюринга”), способная оперировать некоторыми символами на бумажной ленте по некоторым правилам, также способна выполнять любые вычисления. Одним словом, материя не просто обладает способностью к любым вполне определенным вычислениям, но и может производить их самыми разнообразными способами.
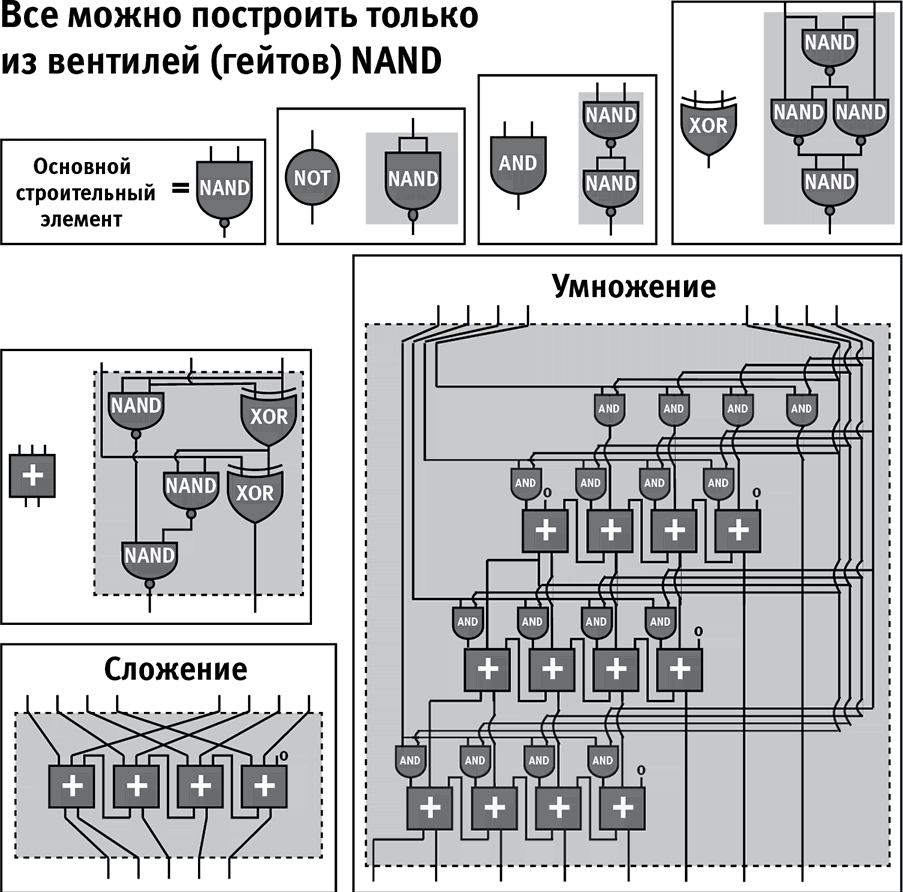
Рис. 2.7
Любое вполне определенное вычисление может быть выполнено при помощи комбинации гейтов одного-единственного типа NAND. Например, у модулей, выполняющих сложение и умножение и представленных на рисунке выше, на вход подается по два бинарных числа, каждое из которых представлено 4 битами, а на выходе получается бинарное число, представленное 5 битами в первом случае, и бинарное число, представленное 8 битами во втором. Менее сложные модули NOT, AND, XOR и “+” (сложение трех одиночных битов в бинарное число, представляемое 2 битами) комбинируются из гейтов NAND. Полное понимание этой схемы исключительно сложно и абсолютно не нужно для дальнейшего чтения книги; я поставил ее здесь исключительно для иллюстрации идеи универсальности, ну и потакая своему внутреннему гику.
Как уже говорилось, Тьюринг в своей памятной статье 1936 года доказал также кое-что значительно более важное: если только компьютер обладает способностью производить некий весьма незначительный минимум операций, он универсален – в том смысле, что при достаточном количестве ресурсов он может сделать все то, на что способен любой другой компьютер. Он доказал универсальность “компьютера Тьюринга”, а приближая его к физическому миру, мы только что показали, что семейство универсальных компьютеров включает в себя такие разные объекты, как сеть гейтов NAND или сеть соприкасающихся нейронов. Более того, Стивен Вольфрам заявил, что большая часть нетривиальных физических систем, от меняющейся погоды до мыслящего мозга, становятся универсальным компьютером, если позволить им как угодно менять свои размеры и не ограничивать их во времени.
Этот самый факт – а именно, что одно и то же вычисление может быть произведено на любом универсальном компьютере, как раз и означает, что вычисление не зависит от субстрата в том же самом отношении, в каком от него не зависит информация: каков бы физический субстрат ни был, оно живет там свою жизнь. Если вы – суперумный персонаж какой-то компьютерной игры будущего, обладающий сознанием, вам никогда не удастся узнать, породила ли вас рабочая станция под Windows, MacBook под MacOS или смартфон с Android, потому что вы субстрат-независимы. У вас не окажется и никаких способов определить, какого рода транзисторы используются микропроцессором этого компьютера.
Поначалу эта базовая идея субстрат-независимости привлекла меня тем, что у нее есть большое количество красивых иллюстраций в физике. Например, волны: у них есть разнообразные свойства – скорость, длина волны, частота, и физики могут решать связывающие их уравнения, совершенно не думая о том, как именно субстрат тут волнуется. Если вы слышите что-то, то вы регистрируете звуковые волны, распространяющиеся в той смеси газов, которую мы называем воздухом, и мы можем рассчитать относительно этих волн все что угодно – что их интенсивность уменьшается как квадрат расстояния, или как они проходят через открытую дверь или отражаются от стен, производя эхо, – ничего не зная о составе воздуха. На самом деле нам даже не обязательно знать, что он состоит из молекул: мы можем отвлечься ото всех подробностей относительно кислорода, азота или углекислого газа, потому что единственная характеристика этого субстрата, которая имеет значение и которая входит в знаменитое волновое уравнение, – это скорость звука, которую нам несложно померить и которая в данном случае будет равна примерно 300 метрам в секунду. Я рассказывал об этом волновом уравнении своим студентам на лекциях прошлой весной и говорил им, в частности, о том, что его открыли и им стали успешно пользоваться еще задолго до того, как физики установили, что молекулы и атомы вообще существуют!
Этот пример с волновым уравнением позволяет сделать три вывода. Во-первых, независимость от субстрата еще не означает, что без субстрата можно обойтись, но только лишь – что многие подробности его устройства не важны. Вы не услышите никакого звука в безвоздушном пространстве, но если замените воздух каким-нибудь другим газом, разницы не заметите. Точно так же вы не сможете производить вычисления без материи, но любая материя сгодится, если только ее можно будет организовать в гейты NAND, в нейронную сеть или в какие-то другие исходные блоки универсального компьютера. Во-вторых, субстрат-независимые явления живут свою жизнь, каков бы субстрат ни был. Волна пробегает по поверхности озера, хотя ни одна из молекул содержащейся в нем воды не делает этого, они только ходят вверх и вниз наподобие футбольных фанатов, устраивающих “волну” на трибуне стадиона. В-третьих, часто нас интересует именно не зависящий от субстрата аспект явления: серфера обычно заботят высота волны и ее положение, а никак не ее молекулярный состав. Мы видели, что это так для информации, и это так для вычислений: если два программиста вместе ловят глюк в написанном ими коде, они вряд ли будут обсуждать транзисторы.
Мы приблизились к возможному ответу на наш исходный вопрос о том, как грубая физическая материя может породить нечто представляющееся настолько эфемерным, абстрактным и бестелесным, как разум: он кажется нам таким бестелесным из-за своей субстрат-независимости, из-за того, что живет своей жизнью, которая не зависит от физических деталей его устройства и не отражает их. Говоря коротко, вычисление – это определенная фигура пространственно-временного упорядочения атомов, и важны здесь не сами атомы, а именно эта фигура! Материя не важна.
Другими словами, “хард” здесь материя, а фигура – это “софт”. Субстрат-независимость вычисления означает, что AI возможен: разум не требует ни плоти, ни крови, ни атомов углерода.
Благодаря этой субстрат-независимости изобретательные инженеры непрерывно сменяют одну технологию внутри компьютера другой, радикально улучшенной, но не требовавшей замены “софта”. Результат во всех отношениях нагляден в истории запоминающих устройств. Как показывает рис. 2.8, стоимость вычисления сокращается вдвое примерно каждые два года, и этот тренд сохраняется уже более века, снизив стоимость компьютера в миллион миллионов миллионов (в 1018) раз со времен младенчества моей бабушки. Если бы все сейчас стало в миллион миллионов миллионов раз дешевле, то сотой части цента хватило бы, чтобы скупить все товары и услуги, произведенные или оказанные на Земле в тот год. Такое сильное снижение цены отчасти объясняет, почему сейчас вычисления проникают у нас повсюду, переместившись из отдельно стоящих зданий, занятых вычисляющими устройствами, в наши дома, автомобили и карманы – и даже вдруг оказываясь в самых неожиданных местах, например в кроссовках.

Рис. 2.8
С 1900 года вычисления становились вдвое дешевле примерно каждые пару лет. График показывает, какую вычислительную мощность, измеряемую в количестве операций над числами с плавающей запятой в секунду (FLOPS), можно было купить на тысячу долларов. Частные случаи вычислений, которые соответствуют одной операции над числами с плавающей запятой, соответствуют 105 элементарным логическим операциям вроде обращения бита (замены 0 на 1, и наоборот) или одного срабатывания гейта NAND.
Почему развитие наших технологий позволяет им удваивать производительность с такой регулярной периодичностью, обнаруживая то, что математики называют экспоненциальным ростом? Почему это сказывается не только на миниатюризации транзисторов (тренд, известный как закон Мура), но, и даже в большей степени, на развитии вычислений в целом (рис. 2.8), памяти (рис. 2.4), на море других технологий, от секвенирования генома до томографии головного мозга? Рэй Курцвейл называет это явление регулярного удвоения “законом ускоряющегося возврата”.
В известных мне примерах регулярного удвоения в природных явлениях обнаруживается та же самая фундаментальная причина, и в том, что нечто подобное происходит в технике, нет ничего исключительного: и тут следующий шаг создается предыдущим. Например, вам самим приходилось переживать экспоненциальный рост сразу после того, как вас зачали: каждая из ваших клеточек, грубо говоря, ежедневно делится на две, из-за чего их общее количество возрастает день за днем в пропорции 1, 2, 4, 8, 16 и так далее. В соответствии с наиболее распространенной теорией нашего космического происхождения, известной как теория инфляции, наша Вселенная в своем младенчестве росла по тому же экспоненциальному закону, что и вы сами, удваивая свой размер за равные промежутки времени до тех пор, пока из крупинки меньше любого атома не превратилась в пространство, включающее все когда-либо виденные нами галактики. И опять причина этого заключалась в том, что каждый шаг, удваивающий ее размер, служил основанием для совершения следующего. Теперь по тому же закону стала развиваться и технология: как только предыдущая технология становится вдвое мощнее, ее можно использовать для создания новой технологии, которая также окажется вдвое мощнее предыдущей, запуская механизм повторяющихся удвоений в духе закона Мура.
Но с той же регулярностью, как сами удвоения, высказываются опасения, что удвоения подходят к концу. Да, действие закона Мура рано или поздно прекратится: у миниатюризации транзистора есть физический предел. Но некоторые люди думают, что закон Мура синонимичен регулярному удвоению нашей технической мощи вообще. В противоположность им Рэй Курцвейл указывает, что закон Мура – это проявление не первой, а пятой технологической парадигмы, переносящей экспоненциальный рост в сферу вычислительных технологий, как показано на рис. 2.8: как только предыдущая технология перестает совершенствоваться, мы заменяем ее лучшей. Когда мы не можем больше уменьшать вакуумные колбы, мы заменяем их полупроводниковыми транзисторами, а потом и интегральными схемами, где электроны движутся в двух измерениях. Когда и эта технология достигнет своего предела, мы уже представляем, куда двинуться дальше: например, создавать трехмерные интегральные цепи или делать ставку на что-то отличное от электронов.
Никто сейчас не знает, какой новый вычислительный субстрат вырвется в лидеры, но мы знаем, что до пределов, положенных законами природы, нам еще далеко. Мой коллега по MIT Сет Ллойд выяснил, что это за фундаментальный предел, и мы обсудим его в главе 6, и этот предел на целых 33 порядка (то есть в 1033 раза) отстоит от нынешнего положения вещей в том, что касается способности материи производить вычисления. Так что если мы будем и дальше удваивать производительность наших компьютеров каждые два – три года, для достижения этой последней черты нам понадобится больше двух столетий.
Хотя каждый универсальный компьютер способен на те же вычисления, что и любой другой, некоторые из них могут отличаться от прочих своей высокой производительностью. Например, вычисление, требующее миллионов умножений, не требует миллионов различных совершающих умножение модулей с использованием различных транзисторов, как показано на рис. 2.6, – требуется только один такой модуль, который можно использовать многократно при соответствующей организации ввода данных. В соответствии с этим духом максимизации эффективности большинство современных компьютеров действуют согласно парадигме, подразумевающей разделение всякого вычисления на много шагов, в перерывах между которыми информация переводится из вычислительных модулей в модули памяти и обратно. Такая архитектура вычислительных устройств была разработана между 1935 и 1945 годами пионерами компьютерных технологий – такими, как Алан Тьюринг, Конрад Цузе, Преспер Эккерт, Джон Мокли и Джон фон Нейман. Ее важная особенность заключается в том, что в памяти компьютера хранятся не только данные, но и его “софт” (то есть программа, определяющая, что надо делать с данными). На каждом шагу центральный процессор выполняет очередную операцию, определяющую, что именно надо сделать с данными. Еще одна часть памяти занята тем, чтобы определять, каков будет следующий шаг, просто пересчитывая, сколько шагов уже сделано, она так и называется – счетчик команд: это часть памяти, где хранится номер исполняемой команды. Переход к следующей команде просто прибавляет единицу к счетчику. Для того чтобы перейти к нужной команде, надо просто задать программному счетчику нужный номер – так и поступает оператор “если”, устраивая внутри программы петлевой возврат к уже пройденному.
Современным компьютерам удается значительно ускорить выполнение вычислений, проводя их, что называется, “параллельно”, в продолжение идеи повторного использования одних и тех же модулей: если вычисление можно разделить на части и каждую часть выполнять самостоятельно (поскольку результат одной не требуется для выполнения другой), то тогда эти части можно вычислять одновременно в разных составляющих “харда”.
Идеально воплощение параллельности достигается в квантовом компьютере. Пионер теории квантовых вычислений Дэвид Дойч утверждал в полемическом запале, что “квантовый компьютер распределяет доступную ему информацию по бесчисленному множеству копий себя самого во всем мультиверсуме” и решает благодаря этому здесь, в нашей Вселенной, любую задачу гораздо быстрее, потому что, в каком-то смысле, получает помощь от других версий самого себя. Мы пока еще не знаем, будет ли пригодный для коммерческого использования квантовый компьютер создан в ближайшие десятилетия, поскольку это зависит и от того, действительно ли квантовая физика работает так, как мы думаем, и от нашей способности преодолеть связанные с его созданием серьезнейшие технические проблемы, но и коммерческие компании, и правительства многих стран мира вкладывают ежегодно десятки миллионов долларов в реализацию этой возможности. Хотя квантовый компьютер не поможет в разгоне заурядных вычислений, для некоторых специальных типов были созданы изобретательные алгоритмы, способные изменить скорость кардинально – в частности, это касается задач, связанных со взломом криптосистем и обучением нейронных сетей. Квантовый компьютер также способен эффективно симулировать поведение квантово-механических систем, включая атомы, молекулы и новые соединения, заменяя измерения в химических лабораториях примерно в том же ключе, в каком расчеты на обычных компьютерах заменили, сделав ненужными, измерения в аэродинамических трубах.
Назад: Что такое память?
Дальше: Что такое обучение?

