Книга: Организованный ум. Как мыслить и принимать решения в эпоху информационной перегрузки

Приложение. Как строить четырехпольные таблицы

Рассуждая о медицине в логическом ключе, мы часто сталкиваемся с такими редкими заболеваниями, что даже положительные анализы не говорят об их наличии. Большое количество фармацевтической продукции настолько редко действует как нужно, что вероятность проявления побочных эффектов гораздо выше возможной пользы. Четырехпольные таблицы позволяют легко рассчитать вероятность, задав байесовский вопрос: «Какова вероятность того, что я болен некой болезнью, учитывая, что у меня положительные анализы?» или «Какова вероятность того, что лекарство мне поможет, учитывая, что у меня есть такие-то симптомы?»

Здесь я приведу пример из главы 6 с несуществующей болезнью, блуритом. Давайте вспомним, о чем шла речь.

• Вы сдаете анализы на гипотетическую болезнь – и получаете положительный результат.

• Основной показатель для блурита – 1 случай из 10 000, или 0,0001.

• Если лечиться хлорогидроксиленом, то существует вероятность 5%, или 0,05, что у вас проявятся побочные эффекты.

• Анализы на блурит в 2% случаев, или 0,02, оказываются неверными.

Вопрос: принимать лекарство или нет?

Для начала построим четырехпольную таблицу и подпишем ячейки.

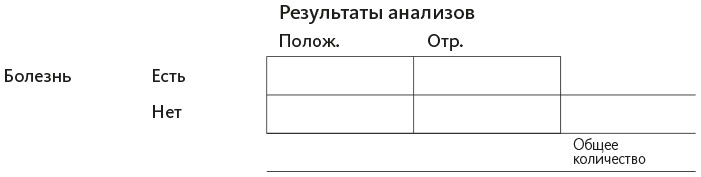
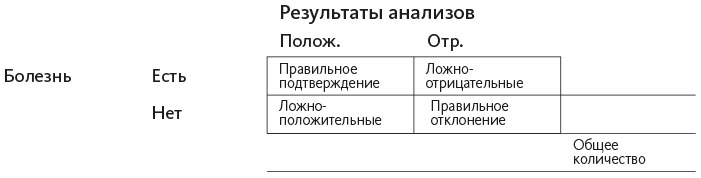
Ячейки внутри позволяют распределить данные на взаимоисключающие категории:

• люди с положительными результатами анализов, у которых есть заболевание (верхняя левая ячейка внутри). Назовем ее ПРАВИЛЬНОЕ ПОДТВЕРЖДЕНИЕ.

• люди с отрицательными результатами анализов, у которых есть заболевание (верхняя правая ячейка внутри). Назовем ее ЛОЖНООТРИЦАТЕЛЬНЫЕ.

• люди с положительными результатами анализов, у которых нет заболевания (нижняя левая ячейка внутри). Назовем ее ЛОЖНОПОЛОЖИТЕЛЬНЫЕ.

• люди с отрицательными результатами анализов, у которых нет заболевания (нижняя правая ячейка внутри). Назовем ее ПРАВИЛЬНОЕ ОТКЛОНЕНИЕ.

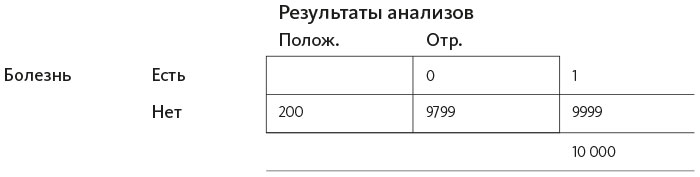
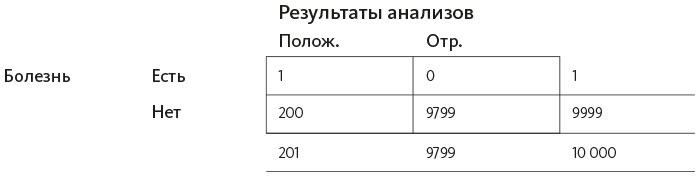
Начнем заполнять известные данные. Основной показатель болезни – 1 из 10 000. В нижнем правом углу, за пределами большой ячейки, напишем «общее население» – 10 000. Я говорю «население», потому что это общее количество человек, которое мы рассматриваем (могли бы взять 380 миллионов человек, живущих в США, а затем изучить все случаи за год – 38 000, но мне удобнее заполнять таблицу меньшими числами, потому что с ними легче обращаться и представить себе «масштабы катастрофы»).

Теперь с помощью этой таблицы нужно посчитать данные во всех остальных ячейках, как в основных четырех внутри, так и снаружи. Мы знаем: один человек из этих 10 000 болеет блуритом. Пока не видим результатов анализов, поэтому пишем цифру 1 справа в поле «Болезнь: есть», показывая наличие болезни.

То, каким образом организована таблица, когда значения идут сверху вниз и слева направо, предполагает, что сумма этих значений заполняется на полях за ее пределами. Это логично: если количество заболевших равно единице, а общее число – 10 000, мы знаем, сколько людей не болеют: 10 000 – 1 = 9999. Впишем.

От врача мы знаем (об этом я писал выше), что в 2% случаев анализы дают неправильные результаты. Из 9999 незаболевших 2% получили неверные анализы, предполагающие диагноз, в том смысле, что они не болеют, но результаты анализов положительные (ложноположительные, нижнее левое поле). Считаем 2% × 9999 = 199,98, округляем до 200.

Теперь, ввиду того, что нам нужно заполнить данные и по горизонтали, и по вертикали, можно посчитать здоровых людей, результаты анализов у которых были отрицательные, то есть правильное отклонение. Это 9999 – 200 = 9799.

Теперь заполним данные о другой ошибке в постановке диагноза: 2% ложноотрицательных. Эти результаты означают, что человек на самом деле болен, а по результатам анализов – нет. Это количество представлено в верхнем правом поле. Болен (как мы видим в таблице, посмотрев на правое поле за пределами основных ячеек) один человек. Тогда считаем 2% × 1 = 0,2, округляем до 0.

И конечно, давайте теперь заполним оставшееся пустое поле – вписываем туда 1 (это значение получилось так: от 1 в боковом поле, которую мы вписали вначале, вычитаем 0, записанный в верхнее правое поле, поскольку у нас должны быть заполнены все ячейки).

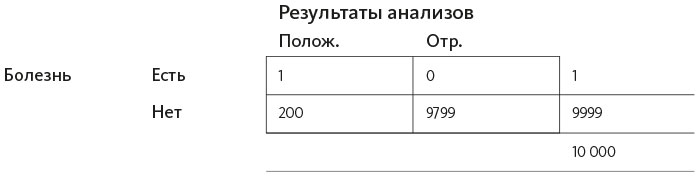
Теперь, чтобы действительно заполнить всю таблицу, выпишем значения в нижние поля за пределами основных ячеек. Чтобы узнать общее количество человек с положительными результатами анализов, просто сложим значения в колонке: 1 + 200 = 201. Общее количество человек с отрицательными результатами анализов: 0 + 9799 = 9799.

Уже отсюда мы можем решить задачу так, как показано в главе 6.

1. Какова вероятность того, что вы больны, учитывая, что результаты анализов положительные? Традиционно мы заменяем слово «учитывая» специальным символом – |, а слово «вероятность» – буквой «р», чтобы написать уравнение примерно в таком виде:

1.1. p (Есть заболевание | анализы положительные)

Это удобный формат записи, потому что так мы видим: первая часть предложения, то есть все, что до знака |, – это числитель (верхняя часть уравнения), а все, что после – знаменатель.

Чтобы ответить на вопрос 1, мы смотрим только на левую колонку, где записаны результаты людей с положительными анализами. Есть один человек из 201, у кого на самом деле есть заболевание и при этом анализы получились положительными. Ответ на вопрос 1: 1/201, или 0,49%.

2. Какова вероятность того, что анализы окажутся положительными, учитывая, что у вас есть заболевание?

2.1. p (Анализы положительные | есть заболевание).

Здесь мы смотрим только на верхний ряд, и дробь получается 1/1. Это говорит о том, что вероятность получить положительные анализы при наличии заболевания равна 100%.

Не забывайте, что хлорогидроксилен, гипотетическое лекарство, о котором я говорил, в 20% случаев дает побочные эффекты. Если бы лечили всех, то есть 201 человека с положительными анализами на блурит, то 20% из них – 40 человек – получили бы побочные эффекты. Помните, что на самом деле болеет только один человек, а лечение в 40 раз чаще приводит к побочным эффектам, нежели выздоровление.

В обоих описанных в шестой главе случаях, как с блуритом, так и с «синей» болезнью, даже при положительных анализах вряд ли вы оказываетесь больным. Конечно, если вы на самом деле болеете, очень важно подобрать правильное лекарство. Что можно сделать?

Стоит сдать анализы второй раз. Мы применяем закон умножения вероятностей, считая, что результаты анализов независимы. То есть любые ошибки могут случайно привести к тому, что только у вас из всех, кто сдавал анализы, получится неверный результат. Это совсем не значит, что у кого-то в лаборатории на вас зуб, поэтому если вы получили некорректный результат однажды, то шансы получить ошибку второй раз у вас не больше, чем у кого-то другого. Вспомните, я говорил, что существует двухпроцентная вероятность того, что анализы окажутся неверными. Рассчитать вероятность того, что лаборант два раза подряд ошибется, можно 2% × 2%, или 0,0004. Если вы предпочитаете дроби, то вероятность 1/50, и 1/50 × 1/50 = 1/2500. Но даже эта статистика не включает основной показатель, то есть то, насколько редко встречается эта болезнь. И основной посыл раздела: это нужно делать.

Безусловно, очень поможет, если вы и в этом случае построите четырехпольную таблицу и ответите на вопрос «Какова вероятность того, что я болею, учитывая, что я два раза подряд получил положительный анализ?»

Когда мы начинали рассматривать блурит, у нас была только гора цифр, и мы расставляли их в таблицу. Так было проще посчитать скорректированную вероятность. Одна из особенностей байесовского вывода в том, что вы можете поместить скорректированные данные в новую четырехпольную таблицу. И каждый раз, обновляя информацию, строить новую таблицу и фокусировать внимание на все более точных оценках.

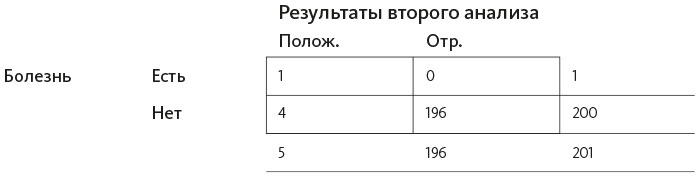
Вот так выглядит заполненная таблица:

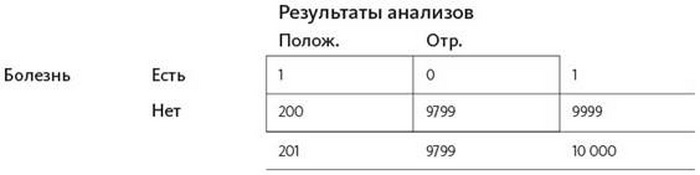
И по ней мы видим:

• Количество человек с положительными результатами анализов: 201

• Количество человек с положительными результатами анализов, имеющие заболевание: 1

• Количество человек с положительными результатами анализов, не имеющие заболевания: 200.

Обратите внимание, мы сейчас рассматриваем только ту половину таблицы, где собраны данные людей с положительными результатами анализов. Это потому, что вопрос, на который мы хотим ответить, предполагает у вас положительные результаты: «Какова вероятность того, что я на самом деле болею, если два раза подряд анализы получились положительными?»

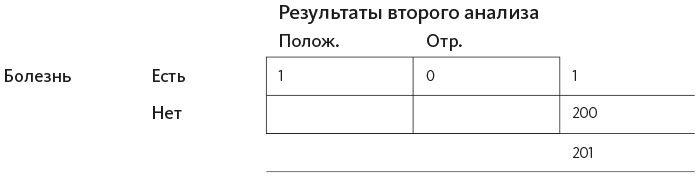
Теперь построим новую таблицу с имеющейся информацией. Как видно из заголовков ячеек, второй анализ может быть положительным или отрицательным, у вас может быть заболевание, а может не быть, но теперь мы рассматриваем не все население в 10 000 человек, а только тех из этого количества, у кого положительные анализы, то есть 201 человека. И теперь в ячейку «Все население» в нижнем правом поле мы записываем 201.

Можно сразу добавить дополнительную информацию, которая встречалась выше. Мы знаем количество человек, среди которых проводим исследование и которые либо болеют, либо нет. Мы добавляем это число в правое поле.

Вернемся к первоначально предоставленным данным: анализ показывает неправильные результаты в 2% случаев. Один человек действительно болен; в 2% случаев диагноз неверный, а в 98% – верный: 2% от 1 = 0,02. Я округлю этот результат до 0 – это и будет количество человек с ложноотрицательными результатами (заболевание есть, но второй раз его неправильно определили). А 98% от 1 – очень близко к 1.

Теперь давайте применим тот же показатель ошибок, 2%, к результатам тех, у кого нет заболевания. 2% из 200 здоровых людей, чьи анализы окажутся положительными: 2% от 200 = 4. Остается 196 человек, кого диагностировали правильно; это количество запишем в нижнем левом поле внутри таблицы. Пусть вас не беспокоит, что числа не целые.

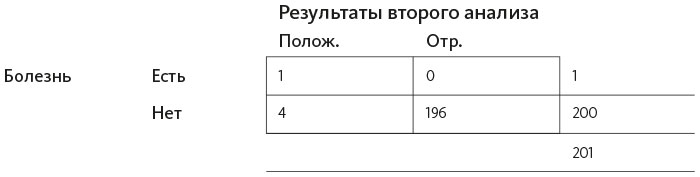
Можно заполнить оставшиеся поля, сложив результаты в колонках: для этого нужно суммировать новые получившиеся вероятности.

Как и ранее, мы смотрим на левую колонку, потому что нас интересуют только люди с положительными результатами второго анализа.

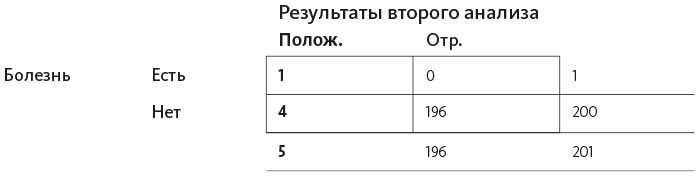
Из пятерых людей, сдавших анализы второй раз, болеет только один: 1 : 5 = 0,2. Другими словами, болезнь действительно настолько редкая, что, даже если два раза подряд получить положительный результат анализа, все равно 20%, что вы больны, а 80% – что нет.

Что же с побочными эффектами? Если начать лечить хлорогидроксиленом всех, кто два раза получил положительный ответ, учитывая, что 20% получат побочные эффекты, то их получит 1 человек, то есть 20% от 5. Из каждых пятерых, кому назначат лечение, одному оно поможет (потому что он на самом деле болеет) и у одного будут побочные эффекты. В этом случае, если сдать анализ два раза, у вас в сорок раз повышается вероятность вылечиться, а не получить побочные эффекты. Прекрасные перемены по сравнению с тем, что было раньше.

Чтобы пойти дальше, возьмем байесовскую статистику. Предположим, согласно данным только что опубликованного исследования, если вы – мужчина, шансы заболеть у вас в десять раз выше. Можно построить еще одну таблицу, чтобы учесть эту информацию, а также сделать более точной оценку вероятности того, что у вас на самом деле может быть заболевание.

В реальной жизни вычисление вероятности применяется гораздо шире, чем только для медицинских решений. Я спрашивал Стива Винна, владельца пяти казино (в отелях Bellagio, Wynn и Encore в Лас-Вегасе, и Wynn Palace в Макао): «Вас не беспокоит, хотя бы чуть-чуть, когда посетители выходят с большими мешками ваших денег?»

• Я всегда счастлив, когда люди выигрывают. Именно это и создает азарт в казино.

• Да ладно, правда? Это ваши деньги. Иногда люди забирают миллионы.

• Наверняка вам известно, что, во-первых, мы зарабатываем куда больше денег, чем выплачиваем в случае выигрыша. Во-вторых, обычно средства к нам возвращаются. За все эти годы я ни разу не видел, чтобы человек ушел с большим выигрышем навсегда. Он приходит в казино снова и ставит все полученные деньги, и мы обычно забираем все назад. Причина, по которой они играют, состоит, в первую очередь, в том, что, как и большинству людей, потакающих своим слабостям – таким как гольф или дорогое вино, – игра им нравится больше, чем деньги. Победа дает капитал для игры без необходимости выписывать чек. Люди теряют 100 центов на доллар, а выигрывают 99 центов. Этот 1% – наша маржа.

Ожидаемая выгода от ставки казино всегда на руку владельцам. Психология игрока заставляет того, кто выиграл большую сумму и мог бы уйти восвояси со всеми деньгами, остаться и проиграть их. Даже если не принимать это в расчет и даже если все забирали бы свои выигрыши, в долгосрочной перспективе это все равно было бы выгодно казино. Именно это приводит нас к тому, что мы дополнительно оформляем долгосрочные гарантии на лазерные принтеры, компьютеры, пылесосы, DVD-плееры и тому подобные вещи. Большие розничные дисконт-магазины заставляют оплачивать гарантии, играя на вашем совершенно разумном нежелании платить большие деньги за ремонт только что купленных вещей. Они обещают «ремонт без забот» по премиальной цене. Однако не надо питать иллюзий: этот сервис говорит совсем не о щедрости продавца, все делается исключительно ради денег: для многих розничных магазинов основная выручка идет не от продажи вам вещи, а от продажи гарантии на ее ремонт.

Такие гарантии, как правило, очень невыгодны для вас и выгодны для продавца. Если и существует десятипроцентная вероятность того, что вы ею воспользуетесь, и это сэкономит вам 300 долларов на ремонт, то ожидаемая выгода составит 30 долларов. Если с вас за нее берут 90 долларов, продавец получит 60 долларов сверх ожидаемой выгоды. Они стараются заманить вас под предлогом «Если вещь сломается, то ремонт будет стоить минимум 200 долларов. Гарантия стоит всего 90 долларов, и вы очень сильно выиграете». Но не ведитесь. Вы выиграете только в том случае, если войдете в те 10%, кому понадобится эта услуга. При любом другом раскладе выиграют другие. Что касается принятия решений, связанных с медициной, все точно так же. Можно применить расчеты ожидаемой выгоды относительно целесообразности затрат медицинского лечения. Конечно, существует строго математический метод вычислить выгоду, нет ничего сверхъестественного в том, чтобы использовать таблицы сопряженности признаков. Тем не менее многие предпочитают их за то, что это эвристический метод организации информации, и он позволяет легко увидеть все цифры. Это, в свою очередь, помогает найти возможные ошибки. Фактически большая часть советов в этой книге касательно того, как быть организованным, сводится к созданию систем, помогающих нам видеть ошибки, когда мы их делаем, или справляться с ошибками, которые мы все неизбежно совершаем.

Назад: Глава 9. И все остальное

Дальше: Благодарности