Глава 10
Некоторые сведения из теории вариаций
Преткновение от земли лучше, нежели от языка.
Сирах 20:18
Цель настоящей главы. Эта глава дает читателю несколько простых уроков по теории вариаций. Вариации – это жизнь, а жизнь – это вариации. Не бывает двух одинаковых людей. Один и тот же поезд или самолет каждый раз прибывает на станцию в разное время. Мы тратим разное время на дорогу на работу каждый день независимо от вида транспорта. Любой, кто когда-либо выполнял лабораторную работу на уроке физики, знает, что при измерении одного и того же сопротивления гальванометр каждый раз показывает разные значения. В 1920 году в рамках технического курса профессора Вилбура Хичкока в Университете штата Вайоминг каждый студент должен был сделать 10 кубиков из чистого цемента, 10 – из цемента в пропорции 2:1 и 10 – из цемента в пропорции 4:1. Мы погрузили их в воду, чтобы цемент лучше затвердел, а через три недели измерили сопротивление разрушению получившихся 30 блоков. Результаты по всем 10 блокам чистого цемента разнились. Результаты для блоков, сделанных из цемента в пропорции 2:1, тоже разнились, как и результаты для блоков 4:1. Как это возможно? Я сам их сделал, они все одинаковы. После знакомства с теорией вариаций мы узнали, что такое мера вариабельности и, в частности, что такое вероятная ошибка для каждой партии.
В главе 4 мы говорили о том, как важно учителю понимать вариации. Мы также говорили об общих и особых причинах вариации. В эксперименте с красными бусами мы рассматривали только общие причины (см. главу 7) и поняли, почему в управлении людьми важно понимать разницу между общими и особыми причинами вариаций (см. главу 6).
Анекдот. Юрист, получивший прекрасное образование, но не знакомый со статистической теорией, объясняет каждое дело особой причиной – разница между общими и особыми причинами ему не известна. Актуарий нью-йоркской страховой компании Metropolitan Life каждое утро опаздывает на работу на 12–17 минут, а уже в офисе рассказывает, почему он задержался сегодня. Каждое утро для него – это новое утро, не похожее на все предыдущие. Ему даже в голову не приходит, что он имеет дело с общей причиной вариации. Он ни разу не догадался выйти из дому на 20 минут раньше, сделав запас для общей вариации, и появиться на службе вовремя. Но, возможно, если бы он сумел прийти вовремя, его жизнь стала бы скучной: о чем же тогда говорить каждое утро?
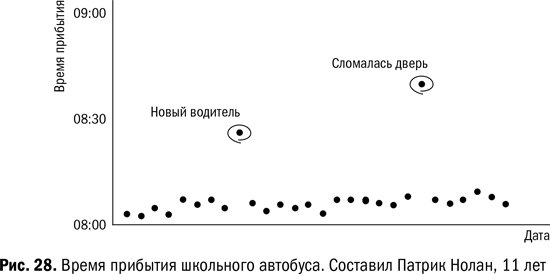
Одиннадцатилетний Патрик и школьный автобус. Доктор Томас В. Нолан однажды показал мне контрольную карту, составленную его 11-летним сыном Патриком. Я воспроизвел ее на рис 28. Ежедневно Патрик фиксировал время прибытия школьного автобуса и показывал его на карте в виде точек. Он легко выделил два дня с особыми причинами опозданий.
Подумайте, как хорошо начинается сознательная жизнь Патрика, если в 11 лет он видит различия между общими и особыми причинами вариаций. Он выявил особые причины без всяких вычислений и дал свое объяснение опозданиям.
Сложно ли составить такую контрольную карту? Патрику это удалось в 11 лет. Это был его научный проект в школе. Хорошее начало жизни.
Очевидно, что некоторые основы теории вариаций можно освоить и в 5-м классе. Ученики окончат школу, вооруженные знаниями, а не только информацией.
Харольд Хотеллинг спрашивал, как можно называться образованным человеку, не имеющему представления о вариациях.
Допустимые 10 %. Инженерам на многих предприятиях позволены 10 % отклонения фактической стоимости проекта от сметной. Эта цифра – 10 % – взята с потолка. На рис. 29 дано фактическое отклонение для 20 проектов в процентах от сметной стоимости. Контрольные пределы показывают, что естественная вариация для этих 20 проектов была на 21 % выше и ниже сметной стоимости.
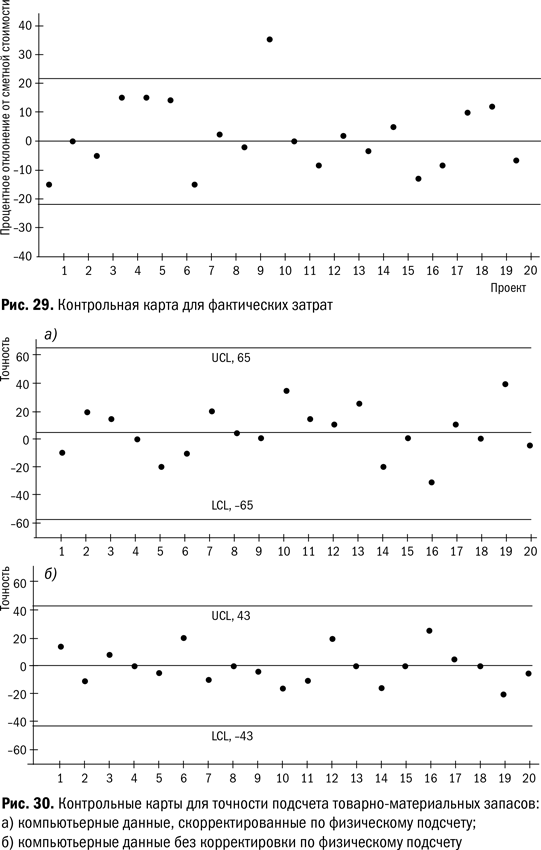
Запасы и компьютерный учет. Для изготовителя продукции со многими стилями и цветами были важны данные по товарно-материальным запасам (как много единиц находится под рукой). Он установил новую компьютерную систему для отслеживания запасов, а после каждого цикла проводил также физический подсчет выхода продукции. Затем результаты физических подсчетов сравнивались с данными компьютера. Если наблюдались несоответствия, компьютерные данные приводились в соответствие с результатами физического подсчета.
Хотя средняя разность приближалась к нулю, первая контрольная карта (а) на рис. 30 показала, что разница между средним и отдельным отклонением могла варьировать от минус 56 до плюс 65 единиц продукции.
Было принято решение корректировать компьютерные данные, только если разница между компьютерным и физическим подсчетом превышает 61 единицу. Вторая контрольная карта (б) была составлена через месяц после введения новой политики. Точность для отдельных отклонений увеличилась на 30 %. Пересмотренные контрольные границы составили ± 43 штуки, и именно они были взяты для дальнейшей корректировки.
Далее следует изучить общие причины отклонений, чтобы уменьшить вариации в будущем.
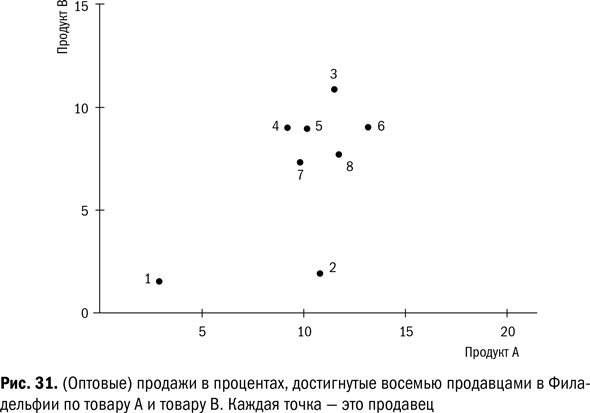
Продавцы. На рис. 31 показан график продаж восьми продавцов в Филадельфии, каждый из них продает два товара: товар А и товар В. Эти цифры мне передал менеджер по продажам одной клиентской компании. Я построил контрольную карту. Совершенно очевидно, что продавец № 1 отстает от других по обоим товарам – А и В. Продавец № 2 отстает по В, но успешно работает с А. Менеджер по продажам хотел заменить продавца № 1: «Вы же видите, что он не справляется со своей работой». Я спросил: на какой территории работает этот продавец? Ответ: Камден.
Следующий вопрос с моей стороны: а вы бы хотели зарабатывать себе на жизнь, продавая эту продукцию в Камдене? Возможно, этот продавец трудится усерднее, чем любой другой. Возможно, он истоптал больше обуви, чем другие, переходя от двери к двери и пытаясь продать свой товар. Возможно, он обзвонил больше потенциальных покупателей, чем любой другой. Может быть, проблема кроется в его территории, а не в нем самом.
Что же делать менеджеру по продажам? Если это проблемная территория, может быть, стоит закрыть там бизнес, пока не улучшится качество продукции компании и цены не упадут до уровня, на котором продавец в Камдене сможет конкурировать с другими.
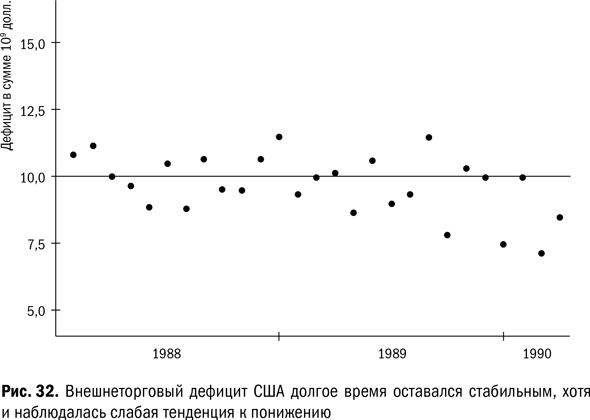
Общие причины вариации торгового дефицита. На рис. 32 представлены данные о внешнеторговом дефиците США за последние 27 месяцев. Подъемы и спады – это просто проявления стабильного процесса. Они генерируют постоянные волны запасов по всему миру. Конечно, подъемы и спады могут быть в будущем и могли быть в прошлом, а особые причины порождаются переменами в нашей экономике.
Заголовки. Очевидно, что нижеприведенные заголовки из газет считают ежемесячные колебания торгового дефицита следствием особых причин.
Аналитики в шоке: торговый дефицит США в июле достиг самого низкого уровня за четыре года, неожиданно для многих аналитиков
Рост импорта резко увеличил торговый дефицит
7,9-миллиардный торговый дефицит в сентябре – это ниже, чем ожидалось
Торговый дефицит США в октябре вырос
Каждый менеджер должен выработать у себя привычку не требовать комментариев по подъемам и спадам (ежедневным, ежемесячным или годовым), вызванным случайными колебаниями (Брайан Джойнер, 28 июля 1992 года).
ЗАМЕЧАНИЯ ОБ ИСПОЛЬЗОВАНИИ ФУНКЦИИ ПОТЕРЬ
Пример простой функции потерь. Функция потерь описывает потери, которые несет система из-за разброса значений регулируемого параметра. Она применима только к тем потерям, которые можно измерить.
Прежде всего, функция потерь помогает нам перейти из мира допусков (то есть соответствия допускам) к непрерывному снижению вариаций относительно цели благодаря совершенствованию процесса.
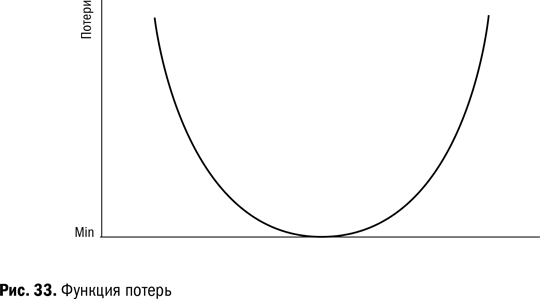
Пример простой функции потерь – результаты работы людей в этой комнате, измеренные в долларах в час. Функция потерь показывает зависимость результатов от температуры в комнате. У каждого человека, работающего в комнате, есть своя функция потерь. Для практических целей мы представили функцию потерь как параболу с вершиной в той точке температуры, при которой достигается максимальный результат (рис. 33). Легко показать, что функция потерь для объединения всех людей в этой комнате также будет параболой. Отклонение от оптимальной температуры вызовет потери. (Кривая не совсем парабола.)
Важно отметить, что из практических соображений мы считаем, что кривая и горизонтальная касательная совпадают на коротком отрезке справа и слева от точки касания. Это означает, что если от оптимального значения отойти на небольшое расстояние, потери будут незначительными. Так, если температура будет всего на два градуса меньше или на два градуса больше оптимальной, снижение производительности труда будет столь незначительным, что им смело можно пренебречь. При большем отклонении потери уже будут значительными. Кто-то должен заплатить за эти потери – доктор Тагути назвал их потерями для общества (сентябрь 1960 года). Мы все платим за ошибку, остановку, плохое управление или банкротство.
Если бы существовала функция потерь с действительными цифрами, мы могли бы подсчитать и сумму, которую целесообразно затрачивать на кондиционирование комнаты. Во сколько обойдется поддержание оптимальной температуры в комнате в пределах двух градусов? В пределах трех градусов? Четырех? Какими будут расходы? Где (в каких пределах) находится точка «равновесия» между потерями (снижением результатов) и расходами на кондиционирование воздуха? Чтобы ответить на эти вопросы, достаточно было бы иметь грубое приближение к функции потерь.
Функция потерь обычно несимметрична. Иногда она очень круто поднимается с одной или другой стороны, иногда – с обеих. Примером может служить концентрация ниобия в стальном листе, нужная для более легкой и успешной сварки. Некоторое количество ниобия в стали нужно обязательно. Если его будет меньше, сварка от этого не улучшится, и можно считать, что ниобий использовался напрасно. Если же содержание ниобия будет больше, чем 3 к 100 тыс., материал тоже будет израсходован напрасно, поскольку он принесет лишь минимальную выгоду.
Реальная функция потерь приведена в моей книге Sample Design in Business Research (Wiley, 1960, p. 294). Она показывает, что нам нужно только подойти близко к оптимальному значению. Очень близко так же хорошо, как и наилучшее приближение.
Еще один пример. Далее мы воспользуемся примером, который привел Уильям Шеркенбах в своей книге The Denting Route, p. 30. Г-н Шеркенбах измерил 50 деталей, сделанных с помощью приспособления, гарантирующего соответствие продукции допускам. Устройство обеспечило идеализированное распределение, представленное как «Вкл.» (рис. 34). Далее г-н Шеркенбах отключил это устройство для следующих 50 деталей и получил идеализированное распределение, представленное как «Выкл.». Любая рациональная функция потерь покажет, что потери с включенным устройством намного превышают потери с выключенным. Иными словами, устройство выполняло свое назначение, но с максимальными затратами. Поэтому намного целесообразнее было его отключить.
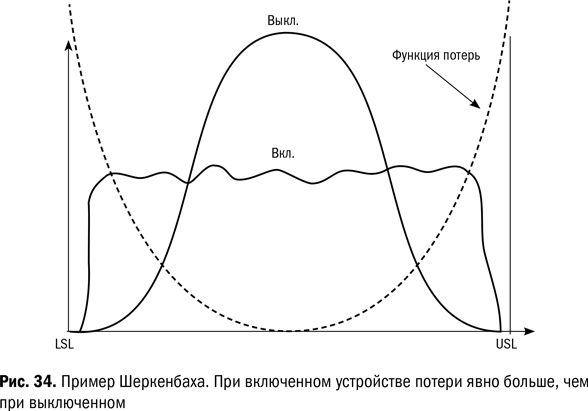
Мы не выступаем против специальных устройств. Просто мы должны знать, как они работают. Мы можем поблагодарить функцию потерь за подсказку.
Следует отметить, что функция потерь не обязательно должна быть точной. Фактически точной функции потерь не существует. Расходы – это не более чем приближенные и грубые прогнозы, но для нашей цели их достаточно.
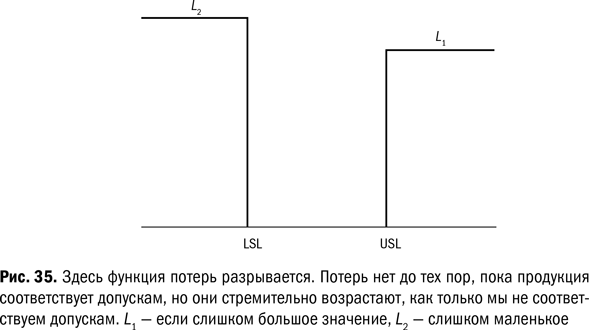
Соответствие допускам. Теперь мы можем рассмотреть возможные потери от соответствия допускам, то есть ноль дефектов. В таком случае функция потерь похожа на ту, которая приведена на рис. 35: она идет вертикально вверх и вниз у обоих границ допуска, между которыми потерь нет. Проверка с использованием измерительной скобы «проходит – не проходит» – это пример соответствия допускам. Мы скоро увидим, что соответствие допускам может привести к серьезным потерям.
Соблюдение сроков. Мы подошли к другому примеру соответствия допускам – посадке на поезд или самолет. Наше время стоит m долл. в минуту. Кривая потерь будет наклонена влево (рис. 36). Появление на платформе за одну минуту до отправления будет стоить нам m долл. потерянного времени; прибытие за две минуты обойдется в 2m долл. и так далее. С другой стороны, если мы пропустим поезд, наши потери составят L долл. Опоздание на полминуты вызовет те же потери, что и опоздание на пять минут. Поэтому функция потерь поднимается скачком вверх от 0 до l.
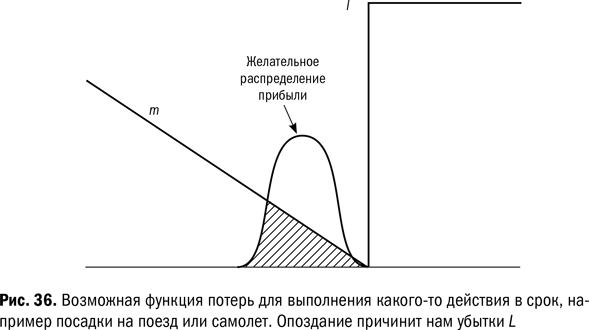
В случае повторяющегося события (например, когда мы садимся на поезд каждый день) мы пытаемся распределить время прибытия, центрируя его так, чтобы «хвост» (трехсигмовая граница) приходился на время отправления. Иными словами, мы пользуемся нашим знанием теории вариаций. В этом случае наши средние потери в день будут описываться заштрихованной зоной под функцией потерь.
Можно усложнить задачу, приняв во внимание, что время отправления поезда также отличается изо дня в день. Существует распределение времени отправления. Его «хвост» может составлять восемь секунд, как в Японии, а может – и полчаса. Однако этот фактор ничего не дает нам в плане понимания и использования функции потерь, поэтому мы его опустим.
Элементарной иллюстрацией будет моя собственная проблема с парковкой; каждое воскресенье мне приходится искать место, где оставить машину перед началом службы в 11:15. Возле церкви есть стоянка для 50 автомобилей. Все места заняты примерно в 10:50, так как водители пьют кофе поблизости после окончания предыдущей службы. Как только они разъезжаются, их места немедленно занимают ожидающие в длинной очереди машины. Если я хочу быть среди них, я должен быть рядом довольно рано. Тот, кто прибывает слишком поздно, не найдет места на парковке: он вынужден искать место на улице, а там его нет. Поэтому лучше приехать раньше, то есть принять потерю времени, и припарковаться на стоянке, чем приехать на минуту позже и столкнуться с полным поражением.
Теория, которую мы здесь изучаем, также применима к предельным срокам. Кто-то зависит от того, закончу ли я свою работу до требуемой даты. Задержка может сорвать весь проект. Чтобы уложиться в срок, я составляю карту требуемых шагов. Лучше указывать диапазон времени или дат, а не жесткие сроки, с поправкой на возможные вариации во времени для любого шага. План, предусматривающий определенную свободу действий, не только придает уверенности, но и позволяет вносить изменения по ходу дела, что может существенно повысить ценность проекта.
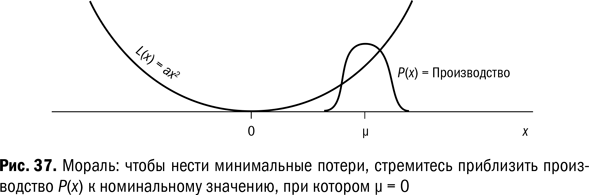
Преимущества номинального значения. Теперь мы готовы формализовать совет, который был повторен уже несколько раз, – не усердствовать чрезмерно с обеспечением допусков. Что еще можно сделать? Мы можем учесть распределение выхода продукции Р(х), которое характеризуется параметрами μ и σ на рис. 37. Будет ли наш выход продукции наилучшей точкой для минимальных потерь? Для функции потерь мы примем Бызфт L(x) = ax2 (парабола), при которой x = 0 в точке минимальных потерь. Тогда потери от производства составят

Очевидно, что потери достигают минимума при μ = 0. Мораль: стремитесь к производству при номинальном значении μ = 0.
Это теория не нова. Мы можем процитировать Джона Бетти, который еще много лет назад, работая в компании Ford Motor, сказал: «В Америке мы всегда волновались по поводу допусков. В отличие от нас японцы волновались по поводу однородности, добиваясь минимальных вариаций относительно номинала».
Мораль: мера рассеивания – сама по себе не показатель достижений. Ее центр гораздо более важен. Несомненно, мы должны стремиться к меньшему рассеиванию в процессе производства практически любой продукции, но это только первый шаг. Следующий важный шаг, как мы только что увидели, это настройка центра на целевое значение.
Эта простая иллюстрация должна положить конец использованию показателей рассеивания, таких как Cpk, поскольку они не имеют никакого значения в плане потерь. Более того, их можно уменьшить до любых значений, просто расширив допуск.
Соответствие допускам, концепция «бездефектного производства», «шесть сигм» и другие «панацеи» – все вполне бесполезны (как отметил Дональд Дж. Уилер в 1992 году).

