Первую нетривиальную теорему в проективной геометрии открыл инженер-архитектор Жерар Дезарг. Ее опубликовал в своей книге в 1648 г. Абрахам Босс. Дезарг доказал следующую важную теорему: «Предположим, треугольники АВС и А´В´С´ находятся в перспективе. Это означает, что три линии, АА´, ВВ´ и СС´, проходят через одну точку. Тогда три точки P, Q и R, в которых пересекаются продолжения трех пар сторон треугольника, лежат на одной прямой». Этот результат теперь нам известен как теорема Дезарга. В ней не упоминаются ни длина, ни углы: она целиком посвящена отношениям между прямыми и точками. А значит, это и есть проективная теорема.

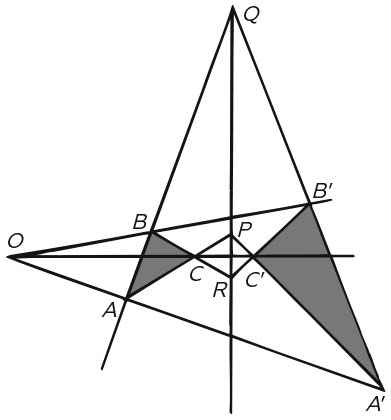
Теорема Дезарга

Есть одна хитрость, делающая теорему очевидной: представьте себе, что рисуете изображение трехмерной фигуры, у которой два треугольника лежат в двух плоскостях. Тогда на линии, по которой пересекаются эти плоскости, и будут расположены три точки Дезарга P, Q и R. Без особого труда так даже можно доказать эту теорему, построив соответствующую трехмерную фигуру, чьи проекции выглядят как два треугольника. Значит, мы можем использовать методы Евклида, чтобы доказывать проективные теоремы.