Пока Фурье не взбаламутил омут, математики купались в приятной уверенности, будто они точно знают, что такое функция. Это был некий определенный процесс f, когда берут число х и получают другое, f(x). Эти числа х вполне логично зависят от f. Если, например, f(x) = 1/x, то x не может быть равно 0. Если f(x) = √x и мы имеем дело с действительными числами, то x должно быть положительным. Но когда дело дошло до точных определений, математики немного растерялись.

Как мы теперь понимаем, причиной затруднений было то, что они пытались свести сразу несколько различных свойств в единую концепцию функции: не просто сформулировать правило, по которому x связано с другим числом, f(x), но найти свойства, которыми обладает это правило: непрерывность, дифференцируемость, возможность быть выраженной в виде формулы и т. д.

В частности, они даже не были уверены, как трактовать функции, имеющие разрыв, например:

Эта функция внезапно скачет от 0 к 1, как только x минует 0. Все почему-то считают, что явной причиной такого прыжка становится изменение формулы: от f(x) = 0 к f(x) = 1. Интуитивно казалось, что это единственное объяснение появления такого скачка; что любая одинарная формула автоматически избавит нас от таких скачков, а значит, небольшое изменение x всегда повлечет за собой небольшое изменение f(x).

Еще одним источником трудностей стали комплексные числа, где – как мы уже видели – такие естественные функции, как квадратный корень, имеют два значения, а комплексные логарифмы – бесконечное множество таковых. Очевидно, что логарифм должен быть функцией, но когда есть бесконечное множество значений, по какому правилу мы получаем f(z) из z? Выходит, таких правил тоже должно быть бесконечно много, и все одинаково годные. Для разрешения всех этих умозрительных разногласий математикам предстояло переломать немало копий. И не кто иной, как Фурье, сумел разом решить их, предложив гениальный ход: расписать любую функцию через бесконечный ряд синусов и косинусов, открытый им в ходе изучения теплопроводности.

Благодаря своей интуиции ученого Фурье понял, что его метод должен быть универсален. Теоретически вы можете представить себе, что удерживаете температуру металлического стержня на значении 0° на одной половине, но при этом сохраняете 10°, или 50°, или сколько необходимо, на остальной его длине. Физиков до сих пор не интересовали разрывные функции, чьи формулы внезапно меняются. Они вообще не имели обыкновения работать с формулами. Мы прибегаем к ним для отображения физической реальности, но это всего лишь техника, наш образ мышления. Конечно, температура окажется иной на стыке этих двух зон, но математические модели всегда имеют какие-то допущения по отношению к физической реальности. Метод Фурье для тригонометрических рядов, приложенный к разрывной функции такого рода, судя по всему, принес ощутимые результаты. Стальные стержни действительно продемонстрировали точно такое распределение температуры, как предсказывало его уравнение теплопроводности, решенное с помощью тригонометрических рядов. В своей «Аналитической теории тепла» он четко описал свою позицию: «В общем, функция f(x) представляет последовательность значений, или ординат, каждая из которых произвольна. Мы не предполагаем, что эти ординаты подлежат общему закону. Они взаимодействуют между собой каждый раз по-своему».

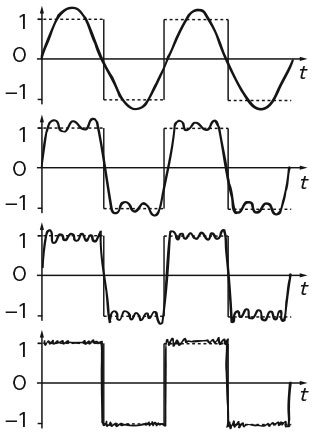
Прямоугольная волна и некоторые ее Фурье-аппроксимации

Отважное утверждение; к сожалению, приведенное доказательство идеи не имело достаточно убедительной математической базы. Фактически оно оказалось еще более ошибочным, чем аргументы Эйлера или Бернулли. Если утверждение Фурье соответствовало истине, то его ряды в итоге могли стать общим законом для разрывных функций. Функция, приведенная выше, со значениями 0 и 1, имеет периодическую родственную прямоугольную волну. И эта волна характеризуется единственным рядом Фурье, причем вполне изящным, работающим одинаково надежно и там, где функция равна 0, и там, где она равна 1. Иными словами, функция, которая кажется представленной двумя разными законами, может быть переписана в рамках одного правила.

Мало-помалу математики XIX в. научились разделять разные концептуальные вопросы в этой сложнейшей области. Первым стало значение самого термина «функция». Вторым – разные способы представления функций: в виде формулы, степенного ряда, ряда Фурье и т. д. Третий вопрос – какими свойствами обладают функции. Четвертый – какое представление функции гарантирует эти свойства. Простой многочлен, например, определяет непрерывную функцию. А обычный ряд Фурье, судя по всему, нет.

Очень быстро анализ Фурье превратился в тест для самой идеи функции. Это обострило проблемы, и важность приобрели скрытые различия технических приемов. Не кто иной, как Дирихле, в 1837 г. предложил современное определение функции в статье, посвященной рядам Фурье. В результате он согласился с Фурье: переменная y является функцией другой переменной x, если для каждого значения x (в определенном диапазоне) задано единственное значение y. Он недвусмысленно утверждал, что здесь не нужны специальный закон или формула – достаточно, чтобы у можно было определить некой четко прописанной последовательностью математических действий, примененных к x. На тот момент должен был казаться экстремальным пример, приведенный им ранее, а именно в 1829 г.: функция f(x) принимает одно значение, когда x – рациональное число, и другое, когда x – иррациональное. Эта функция разрывная в каждой своей точке. (В наше время функции, подобные этой, рассматриваются как довольно невинные, так как возможно гораздо худшее поведение.)

Для Дирихле квадратный корень не был одной двузначной функцией. Это были две однозначные функции. Для действительного x это естественно – но не существенно: взять положительный квадратный корень как одну из них и отрицательный как другую. Для комплексных чисел нет очевидного естественного выбора, хотя какое-то число решений можно найти, чтобы облегчить жизнь.