Еще одна область приложения ДУЧП – притяжение, или теория потенциала. Главной движущей силой развития теории стало изучение силы тяжести – Земли и любой другой планеты. Ньютон представлял планеты как идеальные сферы, хотя их истинная форма ближе к эллипсоиду. И хотя сила притяжения к сфере одинакова с притяжением к точечной частице (для расстояний, выходящих за границы сферы), это нельзя сказать об эллипсоидах.

Колин Маклорен совершил важный рывок в этой области в удостоенном награды труде от 1740 г. «Трактат о флюксиях», изданном в 1742 г. Его первым шагом был поиск доказательства того, что если жидкость однородной плотности вращается с постоянной скоростью под влиянием своей силы тяжести, то наиболее равновесной формой обязательно будет сфероид – эллипсоид вращения. Затем он изучил силы притяжения, создаваемые таким сфероидом, но не очень успешно. Главным результатом было то, что если у двух эллипсоидов одинаковые фокусы и частица находится либо на экваториальной плоскости, либо на оси вращения, то сила притяжения любого сфероида будет пропорциональна их массе.

Эллипсоид

В 1743 г. Клеро продолжил работу над этой проблемой, опубликовав свой труд «Теория фигуры Земли, извлеченная из принципов гидростатики». Но настоящий прорыв совершил Адриен-Мари Лежандр. Он доказал основное свойство, характерное не только для сфероида, но для любого тела вращения. Если вам известна сила тяготения по всей длине оси вращения, вы можете вычислить ее в любой другой точке. Метод Лежандра позволял представить силы тяжести как интеграл в сферических полярных координатах. Умело обращаясь с этим интегралом, он выразил его величину как композицию сферических гармоник, которые определяются специальными функциями, получившими название многочленов Лежандра. В 1784 г. он продолжил работу в этой области, доказав много основных свойств открытых им многочленов. Фундаментальным ДУЧП в теории потенциала является уравнение Лапласа. Его можно найти в пятитомнике «Небесной механики», которую он начал издавать в 1799 г. Схожие идеи уже возникали у его предшественников, но именно Лаплас придал им четкость и завершенность. Уравнение имеет вид:

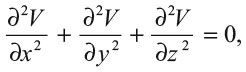
где V(x, y, z) – потенциал точки (x, y, z) в пространстве. Интуитивно он пришел к выводу, что величина потенциала в любой заданной точке составляет среднюю величину от размеров крошечной сферы вокруг нее. Уравнение действительно и вне границ тела: внутри него необходима модификация. Это выражение ныне известно как уравнение Пуассона.