Книга: Укрощение бесконечности. История математики от первых чисел до теории хаоса
Назад: Англия в отстающих
Дальше: Глава 9. Примеры в природе
Дифференциальное уравнение – что это?
Важнейшей идеей, порожденной изобилием трудов об исчислении, стало существование и использование принципиально нового типа уравнений – дифференциальных уравнений. Алгебраические уравнения описывают неизвестную величину с разными степенями. Дифференциальные же гораздо более изощренны: они описывают различные производные от неизвестной функции.
Законы движения Ньютона говорят о том, что если y(t) – высота, на которой частица движется над поверхностью Земли, подвергаясь силе тяготения, то вторая производная d2y/dt2 пропорциональна воздействующей на нее силе g:
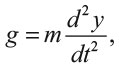
где m – масса. Это уравнение не определяет функцию y напрямую – оно показывает свойства ее второй производной. Чтобы найти саму y, необходимо решить дифференциальное уравнение. Дважды последовательно интегрируя, получим:
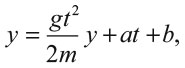
где b – исходная высота частицы, a – начальная скорость. Формула говорит нам, что график, описывающий изменение высоты y относительно времени t, представляет собой параболу, ветви которой направлены вниз. Это наблюдение сделал еще Галилей.
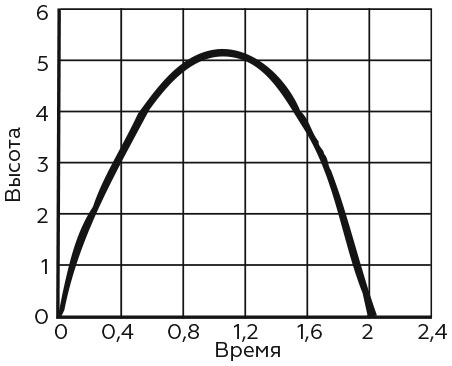
Параболическая траектория снаряда
ЧТО ИСЧИСЛЕНИЕ ДАЕТ НАМ
Современная наука изобилует дифференциальными уравнениями: они оказались наиболее распространенным способом моделирования законов природы. Например, без них не обходится построение траектории полета исследовательских космических зондов, таких как «Маринер», направленный на Марс, или два корабля «Пионер», исследовавших Солнечную систему и предоставивших ученым превосходные снимки Юпитера, Сатурна, Урана и Нептуна, или доставленные на Марс марсоходы «Спирит» и «Оппортьюнити» – шестиколесные роботы, исследовавшие Красную планету.

Марсоход «Спирит» (художественное воспроизведение, НАСА)
Еще один хороший пример – миссия «Кассини», нацеленная на изучение Сатурна и его лун. Среди сделанных в ее рамках открытий – существование морей из жидкого метана и этана на спутнике Сатурна Титане. Конечно, исчисление – далеко не единственный математический метод, примененный в космических исследованиях, но без него ни одна из миссий буквально не оторвалась бы от Земли.Если вернуться на Землю, можно упомянуть любое воздушное судно, автомобиль, движущийся по дороге, подвесной мост или устойчивое к подземным толчкам здание, в создании которых исчисление сыграло важнейшую роль. Даже наше описание того, как относительно времени меняется популяция животных того или иного вида, исходит из дифференциальных уравнений. То же относится к описанию распространения эпидемий, где построенные с помощью исчисления модели помогают разработать эффективные меры подавления эпидемии. Недавно разработанные модели распространения ящура в Великобритании показали недостаточную эффективность принимаемых мер.
Работы Коперника, Кеплера, Галилея и других ученых Возрождения открыли нам математические закономерности, описывающие реальный мир. Одни модели со временем оказались ошибочными, и от них отказались, другие в точности отражали действительность и развивались дальше. Именно в те давние времена выражение «работает как часы» стало всё чаще применяться к нашей Вселенной. Как выяснилось, она живет по строгим, непреложным законам, несмотря на упорные возражения религиозных иерархов, особенно католической церкви.
Величайшим открытием Ньютона стало то, что законы природы проявляют себя не как закономерности некоторых величин, но как взаимоотношения между их производными. Законы природы написаны на языке исчисления, и здесь важны не значения физических переменных, а скорость, с которой они меняются. Это было величайшее прозрение, и оно породило революцию, завершившуюся появлением более-менее современного научного подхода, который навсегда изменил нашу планету.
Назад: Англия в отстающих
Дальше: Глава 9. Примеры в природе

