Книга: Укрощение бесконечности. История математики от первых чисел до теории хаоса
Назад: Аль-джабр
Дальше: Алгебраическая символика
Кубические уравнения
Итак, вавилоняне умели решать квадратные уравнения, и их метод был по существу таким же, какому нас учат сегодня. Алгебраически самое сложное в нем – квадратный корень, и присутствует несколько стандартных арифметических действий (сложение, вычитание, умножение и деление). Ожидаемым следующим шагом становятся кубические уравнения, включающие неизвестное в кубе. Их мы пишем так:
аx3 + bx2 + cx + d = 0,
где x – неизвестное, а коэффициенты a, b и c – известные. Но до появления идеи отрицательных чисел математики классифицировали кубические уравнения по нескольким отдельным видам, так что, например, выражения x3 + 3x = 7 и x3 – 3x = 7 расценивались как совершенно разные, и для них существовали свои методы решения.
ЧИСЛА ФИБОНАЧЧИ
Третья часть «Книги абака» содержит задачу, автором которой, скорее всего, был сам Леонардо: «Некто поместил пару кроликов в место, со всех сторон окруженное стеною. Со второго месяца после своего рождения кролики начинают спариваться и каждый месяц производить новую пару кроликов; кролики никогда не умирают. Сколько пар кроликов будет через год?»Эта каверзная задача приводит к любопытной последовательности чисел, получившей широкую известность:1, 2, 3, 5, 8, 13, 21, 34, 55, …и т. д. Каждое число – сумма двух предыдущих. Их стали называть числами Фибоначчи и они часто встречаются как в математике, так и в мире природы. Например, у многих цветов число лепестков совпадает с числами Фибоначчи. Это следствие особенностей роста растений и геометрии примордиев – зачатков в виде мельчайших скоплений клеток в точке роста, развивающихся в отдельные лепестки.Условия задачи Фибоначчи для воображаемой популяции кроликов нельзя воспроизвести физически, но более общее правило (модель Лесли) используется и по сей день для некоторых задач динамики популяций. Их приходится решать, чтобы предсказать популяционные колебания определенного вида животных с учетом спаривания и смертности.ЧТО АЛГЕБРА ДАЛА ИМ
Многие главы «Книги абака» содержат алгебраические задачи, отвечающие интересам купечества. Одна, не только практическая, выглядит так: «Некто купил 30 птиц – попугаев, голубей и воробьев. Попугай стоит 3 серебряных монеты, голубь 2, а воробей 1/2. Он заплатил 30 серебряных монет. Сколько птиц каждого вида он купил?»Если x обозначает число попугаев, y – число голубей, а z – число воробьев, то в современной системе мы составим уравнения:x + y + z = 30,3x + 2y + 1/2 z = 30.В мире рациональных чисел эти уравнения будут иметь много решений, но в самом вопросе подразумевается дополнительное условие: x, y, z – целые числа. Тогда есть только один ответ: 3 попугая, 5 голубей и 22 воробья.Леонардо также приводит ряд задач, посвященных покупке лошади. Один человек говорит другому: «Если ты дашь мне треть своих денег, я смогу купить лошадь». Тот ему отвечает: «Если ты дашь мне четверть своих денег, я смогу купить лошадь». Сколько стоит лошадь? Сейчас уже найдено много решений; среди целочисленных самая малая цена лошади – 11 серебряных монет.
Греки открыли, как использовать конические сечения для решения некоторых кубических уравнений. Современная алгебра доказала, что если коническое сечение пересекается с другой коникой, точки пересечения находятся с помощью уравнения третьей или четвертой степени (в зависимости от конического сечения). Греки не знали об этом как об общем факте, но использовали следствия из него в некоторых частных случаях, применяя коническое сечение как новый вид геометрического инструмента.
Эта линия атаки была дополнена и приведена в систему персидским ученым Омаром Хайямом, более известным как автор четверостиший рубаи. Примерно в 1075 г. он классифицировал кубические уравнения на 14 видов и показал, как решать каждый из них, используя коники, в своем труде «Трактат о доказательствах задач алгебры и аль-мукабалы». Этот труд стал прорывом в геометрии, в нем практически безукоризненно развит геометрический метод решения кубических уравнений. Кое-кто из современных математиков может это оспорить: некоторые задачи у Хайяма решены не полностью, так как он предполагал, что отдельные точки геометрически определены, хотя иногда их не существует. Причина в том, что иногда он считал, будто его коники пересекаются, хотя на самом деле этого не было. Но всё это лишь незначительные огрехи его трудов.
Итак, геометрические методы решения кубических уравнений были найдены, но существуют ли также и алгебраические решения, где самыми сложными составляющими будут кубические корни? Итальянские математики эпохи Возрождения совершили огромный прорыв в алгебре, найдя положительный ответ на этот вопрос. В то время математики зарабатывали себе репутацию, соревнуясь в публичных состязаниях. Каждый участник предлагал противникам свои задачи, и тот, кто решил больше всех, признавался победителем. Зрители вольны были даже заключать пари на исход соревнования. Ставки порой делали и сами участники: описан случай, когда проигравший был обязан угостить победителя (и его друзей) тридцатью обедами. Кроме того, у хорошо проявивших себя участников состязания появлялась дополнительная возможность обзавестись учениками, особенно среди знатной молодежи. Так или иначе, публичные математические бои стали серьезным мероприятием.
Одна из таких дискуссий состоялась в 1535 г.: предстояло встретиться Антонио Фиоре и Никколо Фонтана по прозвищу Тарталья, «заика». Тарталья разнес Фиоре в пух и прах, и слух о его триумфе дошел до ушей Джероламо Кардано. Тот насторожился. Он как раз трудился над всесторонней книгой об алгебре, как раз над тем разделом, что оказался предметом состязания между Фиоре и Тартальей: кубические уравнения. Тогда было принято делить кубические уравнения на три разных типа – опять-таки из-за нежелания признавать отрицательные числа. Фиоре было известно решение лишь для одного типа. А Тарталья поначалу знал решение только для другого типа. В современной нотации его решение для уравнения типа x3 + ax = b выглядит так:
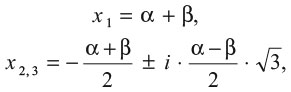
где i – мнимая единица, а
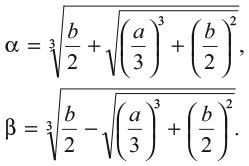
За неделю до состязания Тарталья был в отчаянии и боялся проиграть, но тут его посетило озарение: он понял, как решить остальные типы уравнений. И, конечно, он послал Фиоре только те уравнения, которые тот заведомо не мог решить.
Кардано прослышал об этом соревновании и понял, что оба соперника успели разработать методы для решения кубических уравнений. Мечтая вставить их в свою книгу, он обратился к Тарталье с просьбой поделиться с ним своими наработками. Тарталья, естественно, с неохотой пошел на это, ведь средства к его существованию зависели от них. Он долго колебался, но в итоге всё же его удалось уговорить. Кардано поклялся не публиковать новый метод. Тайна была нарушена в изданном Кардано труде «Великое искусство» («Ars magna»), и Тарталья имел полное право рассердиться. Он публично обвинил Кардано в плагиате.

Хотя Омар Хайям известен большинству из нас как поэт, он был также и выдающимся математиком.
Впрочем, Кардано никогда не мог похвастаться хорошей репутацией. Он был неисправимым игроком, готовым спустить любую сумму в карты, кости или даже шахматы. Так он умудрился проиграть все семейное состояние. С другой стороны, это был гений, талантливый врач, выдающийся математик и опытнейший самопиарщик, хотя его положительные качества часто бледнели на фоне излишней, подчас на грани оскорбления, откровенности. И гнев Тартальи, обвинявшего Кардано в обмане и воровстве, был вполне справедливым. То, что Кардано честно ссылался в своей книге на Тарталью, только усугубило положение. Тот понимал, что в памяти потомков останется автор книги, а не какое-то имя, мельком упомянутое в паре строк.
Но у Кардано было оправдание, и вполне весомое. Оно стоило того, чтобы нарушить обещание, данное Тарталье. Он включил в свою книгу новые открытия, сделанные им и его учеником Лодовико (Луиджи) Феррари, в том числе общее решение уравнения четвертой степени. Это было великое достижение, настоящий прорыв в науке. Конечно, Кардано не преминул включить его в свою книгу. Это считалось вполне законным, ведь открытие сделал его ученик. Однако метод Феррари сводит решение любого уравнения четвертой степени к соответствующему кубическому; следовательно, он основан на методе Тартальи. И Кардано не мог опубликовать работу Феррари, не включив в нее также и метод Тартальи.
А вскоре пришли новости, подсказавшие ему способ выйти из неловкого положения. У того самого Фиоре, что проиграл Тарталье в публичном соревновании, был ученик, Сципион дель Ферро. И до Кардано дошли слухи о том, что дель Ферро решил все три типа кубических уравнений, а не только то, с которым справился Фиоре, и что неопубликованные бумаги дель Ферро оказались в руках некоего Аннибала дель Наве. И вот Кардано с Феррари в 1543 г. отправляются в Болонью, чтобы повстречаться с дель Наве, посмотреть на его бумаги, и там – ясные как день – им открылись решения для всех трех типов уравнений. Итак, у Кардано появилась возможность спокойно заявить, что он опубликовал не метод Тартальи, а открытие дель Ферро.
Но Тарталья не смирился с поражением, хотя и не мог больше опровергать уверения Кардано о том, что приведенное им решение открыто дель Ферро. Тарталья опубликовал пространную и полную гнева диатрибу об этой несправедливости, и его вызвал на публичные дебаты Феррари, горевший желанием отстоять честь наставника. Он одержал грандиозную победу, а Тарталья так и не оправился от этого удара.
Назад: Аль-джабр
Дальше: Алгебраическая символика

